Akademik

МОДЕЛЬЯДРА -теория, основанная на представлении об атомном ядре как о системе нуклонов, движущихся независимо в потенциальном поле, создаваемом др. нуклонами. В более широком смысле с О. м. я. связывают модели ядра, для к-рых этот. н. ср. поле и одночастичное движение нуклонов являются исходными пунктами, а коллективные движения описываются на основе одночастичного. Так понимаемаяО. м. я. - основа большинства совр. микроскопич. подходов в теории ядра. Обычно О. м. я. противопоставляется модели жидкой капли, в к-рой ядро рассматриваетсякак непрерывная среда и движение отд. нуклонов не выделено (см. Капельнаямодель ядра).
О. м. я. возникла в нач. 1930-х гг. поаналогии с моделью электронных оболочек атома. Её появление былосвязано с обнаружением нерегулярностей в поведении энергии связи атомныхядер как ф-ции числа нейтронов в ядре N и протонов Z (массовое число А= N+ Z). Ядра, у к-рых числа N и Z соответствуют наиб. выраженныммаксимумам энергии связи (2; 8; 20; 28; 50; 82 и .= 126), получилиназв. магических ядер. Объяснение существования всех магич. ядербыло дано М. Гёпперт-Майер (М. Goeppert-Mayer) и Й. X. Йенсеном(J. Н.Jensen) [1] и отмечено Нобелевской премией. О. м. я. сыграла большую рольв развитии ядерной физики и в создании микроскопич. подходов в теории ядра.
Одночастичная модель - простейший вариантО. м. я. (нуклоны, движущиеся в ср. поле ядра, не взаимодействуют междусобой). Волновая ф-ция ядра представляется в виде антиспмметризов. произведенияодночастичных волновых ф-ций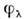 - решений одночастичного Шрёдингера уравнения. Входящий в это ур-ниепотенциал О. м. я. является суммой центрального U_c испин-орбитального U_SL членов. В сферич. ядрах U _с и U_SL зависят только от модуля радиуса-вектора r. В качестве U _с,как правило, берут т. н. потенциал Саксона - Вудса: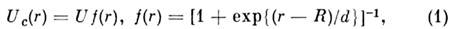

где R =r₀ А ^1/3(r₀- параметр, приближённо равный среднему расстоянию между нуклонами в ядре)и параметр d, определяющий толщину диффузионного слоя, обычно одинаковыдля нейтронов и протонов, а глубина потенциальной ямы U для нейтронови протонов при N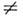Z различна. Она состоит из двух слагаемых: изоскалярного члена U₀,одинакового для нейтронов и протонов, и изовекторного члена U₁,вклад к-рого пропорц. нейтронному избытку и имеет разный знак для нейтронови протонов:

U^n,p = U₀+U_l(N-Z)/A.(2)

Для протонов к (1) добавляется кулоновскпйпотенциал. Его чаще всего аппроксимируют выражением для потенциала равномернозаряженной сферы.
Спин-орбитальный потенциал обычно полагаютсосредоточенным в основном на поверхности ядра. Он апироксимируется выражением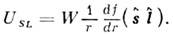

Здесь 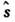и 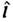- операторы спинового и орбитального угл. моментов, величина W^n,p определяетсяф-лой, аналогичной (2). Существует множество наборов параметров потенциалаО. м. я., типичные их значения: U₀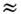- 50 МэВ, U₁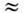20МэВ, r₀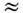1,25 фм, d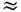0,6 фм, W₀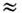W₁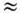12МэВ фм ². Величина U_SL заметно меньше U _с,но значительно превышает ср. энергию взаимодействия 2 нуклонов, к-рая попорядку величины колеблется от U₀/A до U₀/A^2/3, взависимости от суммарного угл. момента взаимодействующей нары. Поэтомув ядрах, за исключением самых лёгких, осуществляется т. н. j - j -связь:орбитальный момент l и спин s складываются в полный угл. момент j нуклона, а векторы j_i отд. нуклонов складываются в полныйугл. момент ядра I.
Состояние нуклона в сферич. ядре характеризуетсяполным моментом j и чётностью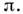 Этоопределяет и орбитальный момент l, т. к. два возможных (по правиламсложения угл. моментов) значения l = j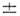¹/₂ отвечаютразл. чётности 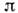=( - 1)^l. Состояния нуклона с одинаковыми l, j нумеруют в порядке увеличения энергии гл. квантовым числом n = 1,2,... (число узлов радиальной волновой ф-ции равно n -1). Разл. состояния нуклона принято обозначать: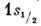( п=1, l =0, j= ¹/₂); lp_1/2,1 р_3/2, 2s_1/2 и т. п. Проекция т вектора j на ось квантования может принимать (2j + 1) значений от - j до + j. В сферич. ядре энергия 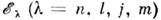не зависит от т и одно частичные уровни (2j + 1) кратно вырождены. В отсутствие U_SL вырожденными были бы и уровни с j= l ±¹/₂. Т. к. матричный элемент 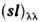по ф-циям 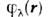зависит от j [равен l/₂ для j= l +¹/₂ и- (l+ 1)/2 для j = l -¹/₂],то включение U_SL снимает это вырождение, причём уровеньс j= l + ¹/₂ опускается вниз, ас j = l -¹/₂, поднимается вверх. Расстояниемежду соответствующими уровнями - спин-орбитальное расщепление 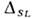пропорц. (2l+ 1). Эта закономерность хорошо подтверждается экспериментально.
Согласно одночастичной О. м. я., нуклоныданного сорта (р или п) заполняют j -уровень (подоболочку). Затемзаполняется след. подоболочка. Подоболочки группируются в оболочки, разделённыеэнергетич. "зазорами", значительно превышающими ср. расстояние между уровнями(2 - 3 МэВ в лёгких ядрах и 0,5 МэВ - в тяжёлых). Эти "зазоры" наз. матовымипросветами (рис.).
Тенденция к группированию подоболочекв оболочки особенно выражена для потенциала гармонич. осциллятора, гдев отсутствие U_SL вырождены все уровни с данным осцилляторнымквантовым числом N = 2(п- 1) + l [2]. Причина этого явлениясвязана с квазиклассич. условиями квантования орбит движения частицы втрёхмерной потенциальной яме [2].
Значения магич. чисел зависят от вида потенциала. На рис. приведена схема уровней для нейтронов и протонов в ²⁰⁸ Рb, рассчитанная для потенциала Саксона - Вудса. В более лёгких ядрах нек-рые детали схемы уровней изменяются, но в целом заполнение уровней происходит в соответствии со схемой (см. рис.). Она демонстрирует возникновение магич. чисел и роль в этом явлении U_SL. Первые оболочки: [(ls_1/2, (1 р_3/2, lp_1/2), (1d_5/2, 2g_1/2, 1d_3/2 )] совпадают с оболочками гармонического трёхмерного сферически симметричного осциллятора, где уровни внутри каждой оболочки были бы полностью вырождены. Почти такое же правило применимо и дальше, но здесь к данной оболочке присоединяется уровень из след. осцилляторной оболочки, имеющей наиб. значение j. Опускание уровней в нпж. оболочку связано с тем, что для дублетов с большими j спин-орбитальное расщепление превосходит по величине матовые просветы. Именно эти спустившиеся в соседнюю оболочку ниж. уровни спин-орбитальных дублетов нейтронов и протонов с максимальными j и обеспечивают правильные значения магич. чисел, кроме самых первых.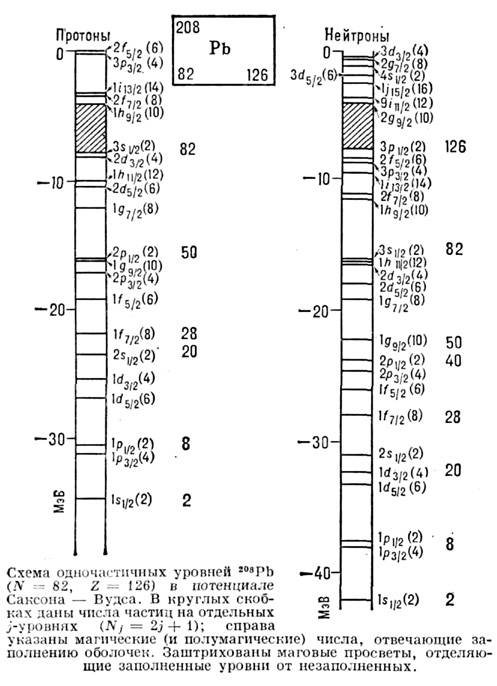

Помимо объяснения природы и правильноговоспроизведения значений магич. чисел одночастичная О. м. я. в большинствеслучаев правильно описывает спины нечётных ядер. Она даёт однозначные предсказаниязначений магн. и квадрупольных электрич. моментов, а также вероятносте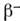й и 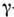-переходовв нечётных ядрах (ядра с нечётным А). Так, магн. момент нечётногоядра в одночастичной О. м. я. (индекс одн.) определяется только последнимнуклоном и даётся простыми ф-лами (Т. Шмидт, Th. Schmidt, 1937), содержащимитолько гиромагн. отношения свободных нуклонов (см. Барионы). Согласноэтим ф-лам, магн. момент [в единицах ядерного магнетона3,1524515(53)х 10^-18 МэВ/Гс] для протонно-нечётного ядра (Z нечётное, . чётное):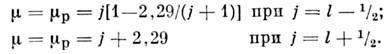

Для нейтронно-нечётного ядра:

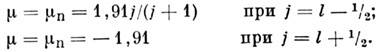
Т. о., в одночастичной О. м. я. магн. моментынечётных ядер должны располагаться на двух парах т. н. линий Шмидта. Эксперим. значения 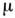всегда находятся между линиями Шмидта, при этом, как правило, отличия 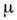от шмидтовских значений порядка 20 - 30%. Магн. моменты нечётно-нечётныхядер с большой точностью равны векторной сумме магн. моментов соответствующихнечётных ядер.
Вероятности эл.-маги. переходов магн. типа связаны с величинами магн. моментов. Так, М1-переходы связаныс излучением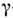 -квантамагн. дипольного излучения при изменении ориентации спинового магн. момента. Эксперим. значения вероятностей перехода В( М1), какправило, отличаются от предсказаний одночастичной О. м. я. не более чемв 2 - 3 раза. Отдельно стоят т. н. l -запрещённые М1-переходы. Это одночастичные переходы с изменением орбитального момента l на2, напр. переход d_3/2 - > S_1/2. В одночастичнойО. м. я. такие переходы строго запрещены, т. к. ответственный за них операторспина не может изменять орбитальный момент частиц. В действительности этипереходы происходят, но с вероятностью, на 2 - 3 порядка меньшей, чем разрешённые М1-переходы, в к-рых l не меняется (напр., d_3/2 - > d_5/2).Снятие l -запрета связано с поправками к одночастичной О. м. я. [2].Магн. переходы высших мультипольностей также качественно объясняются одночастичнойО. м. я.
Характеристики ядер О. м. я. описываетхуже. Электрич. квадрупольный момент протоннонечётного ядра с p_j протонамина незаполненном j -уровне в одно-частичной О. м. я. даётся выражением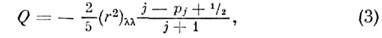

куда входит ср. значение 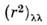от квадрата радиуса по состоянию 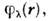зависимость к-рого от деталей потенциала О. м. я. невелика. Ф-ла (3) правильноопределяет знак квадрупольных моментов большинства протонно-нечётных ядер, но расхождения с экспериментом достигают иногда целого порядка. Ещё большерасхождения с экспериментом в случае нейтронно-нечётных ядер. Здесь О. м. я. предсказывает Q= 0, тогда как измеренные значения Qвбольшинстве случаев сравнимы с Qпротонно-нечётных ядер.
Одночастичная О. м. я. предсказывает отсутствиеэлектрич. квадрупольных переходов ( Е2 )в нейтронно-нечётных ядрах, а они идут прибл. с такими же вероятностями, что и в протонно-нечётныхядрах. В последних же расхождения с экспериментом в величине вероятностейещё сильнее, чем в случае квадрупольных моментов. Наиб. сильные расхождениямежду эксперим. и теоретич. значениями квадрупольных моментов и вероятностейэлектрич. квадрупольных переходов наблюдались для ядер в области редкоземельныхэлементов (150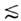 А 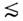180)и актинидов ( А 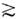220).Именно это обстоятельство наряду с нек-рыми др. фактами (напр., скачокв величине изотопич. смещений уровней атомных s -электронов в районе А 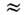150)послужило толчком к предположению о несферичности тяжёлых ядер (см. Деформированныеядра).

Одночастпчные состояния в деформированныхядрах. Идеи О. м. я. были обобщены для описания одночастичных состоянийв деформир. ядрах, где они служат основаниями ротац. полос в нечётных ядрах. Все известные деформированные ядра аксиально симметричны. Кроме того, ониобладают т. н. R -инвариантно-стью - симметрией по отношению к поворотуна угол 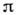относительно любой оси, перпендикулярной оси симметрии z. Статич. моментыдеформир. ядер говорят о близости их формы к форме аксиального эллипсоидас характерными значениями параметра деформации (эксцентриситет эллипсоида)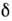~ 0,2 - 0,3. В таком случае не зависящая от спина нуклона часть среднегоядерного потенциала может быть представлена в виде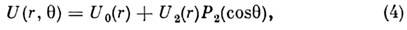

где 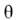- азимутальный угол, Р ₂( х) - полином Лежандра. По масштабувеличины |U₂|~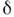|U₀|.Аналогично модифицируется и выражение для U_SL [2].
В аксиальном потенциале полный угл. моментчастицы j не сохраняется, сохраняется лишь его проекция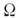 на ось z. При малых деформациях 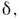рассматривая второй член в (4) как малое возмущение, для уровнен энергииможно получить

где (U₂)_n,l,j -ср. значение U₂(r )по состоянию (n,l, f).Деформация ядра снимает вырождение по |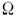|. Остаётся лишь как следствие R-инвариантиости вырождение по знаку 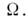В вытянутом ядре энергетически выгоднее состояния с малыми |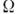|,в сплюснутом - с большими.
Деформация ядра разрушает оболочечнуюструктуру одночастичных уровней. Это происходит из-за того, что уже при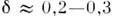 второй член в (5) превосходит по величине маговый просвет между оболочкамисферич. ядра и оболочки перепутываются. Однако при увеличении деформацииснова возникает оболочечная структура, характеризующаяся чередованием сгущенийи разрежений одночастичных уровней.
При больших деформациях требуется численноерешение ур-ния Шрёдингера в деформир. внешнем поле, но качеств. картинуможно понять, рассматривая потенциал анизотропного осциллятора с неравнымичастотами колебаний вдоль (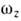 )и перпендикулярно ( 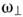)оси z;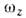и 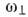связаны с параметром деформации соотношениями: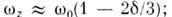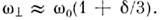В осцилляторном потенциале движение разделяется на независимые колебаниявдоль и перпендикулярно оси z, а энергии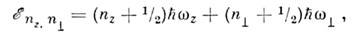

где 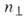= п _х+ п _у - полное число квантов колебания по осям . и у. Т. о., состояния с различными п _х и п _у, нос одним 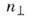вырождены. При значении 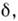при к-ром отношение осцилляторных частот рационально (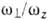= p/q; p, q - целые числа), возникает дополнит. вырожденце уровней, отвечающих одному и тому же значению комбинации 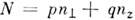(оболочечное квантовое число в деформир. ядрах). Хотя это вырождение по . вреальном ядре снимается из-за отличий ср. поля от потенциала осциллятора, тенденция к восстановлению оболочечной структуры с ростом параметра деформации 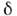сохраняется и для неосцилляторных потенциалов.
Смешивание конфигураций. Многочастичнаямодель оболочек. В более совершенных вариантах О. м. я. помимо ср. полявводится т. н. остаточное взаимодействие между нуклонами, т. е. дополнительноек взаимодействию, формирующему потенциал ср. поля. В результате к основной, одночастпч-ной компоненте волновой ф-ции ядра примешиваются более сложные, многочастичные компоненты (конфигурации). В многочастичной О. м. я. выделяютодин или несколько частично заполненных ("валентных") уровнен поверх инертного"остова" (заполненные оболочки) и пытаются учесть все возможные конфигурациичастиц, находящихся на выделенных уровнях. При этом применяются методытеории групп, к-рые в простейших случаях позволяют однозначно найтимногочастичную волновую ф-цию ядра. С ростом номера оболочки и числа валентныхнуклонов вычислит. трудности быстро растут. Но даже в тех случаях, когдаточный расчёт возможен, из него сложно извлечь физически важную информацию.
Успешней оказались подходы, в к-рых рассматриваютсялишь нек-рые многочастичные конфигурации, связанные с простейшими остовнымивозбуждениями, но кол-во "валентных" уровней достаточно велико или даженеограниченно. Простейшее возбуждение остова отвечает переходу одной изчастиц остова в незаполненное состояние, в результате чего в остове образуется"дырка". Соответствующие конфигурации наз. состояниями типа "частица -дырка". Популярным методом является т. н. приближение случайных фаз, вк-ром учтены возбуждения типа "1 частица - 1 дырка", а также наиб. существенныеиз возбуждений остова типа "2 частицы - 2 дырки".
Учёт смешивания конфигураций объясняет(по крайней мере, качественно) l -запрещённые переходы, отклонениемагн. моментов от линий Шмидта, значения квадрупольных моментов нейтронно-нечётныхядер и нек-рые др. факты, непопятные с точки зрения одночастичной О. м. я. Кроме того, приближение случайных фаз служит основой описания в рамкахО. м. я. коллективных возбуждений четно-чётных ядер - как низколежащихповерхностных колебательных возбуждений ядер, так и гигантскихрезонансов[2].
Одно из наиб. существенных проявленийостаточного взаимодействия - спаривание между нуклонами в ядре и ядернаясверхтекучесть (см. Сверхтекучая модель ядра). Одночастичная О. м. я. с учётом ядерной сверхтекучести в сочетании с капельной моделью применяласьи к вычислению масс ядер и барьеров деления [3].

Обоснование и интерпретация О. м. я. Концепция квазичастиц. По характеру осн. идей О. м. я. тесно связанас таким микроскопия, подходом, как приближение самосогласов. поля. Простейшийвариант теории самосогласов. поля - метод Хартри - Фока в ядрах "работает"плохо из-за сильного взаимодействия между нуклонами. В методе Хартрн -Фока с эфф. силами используется обычная для О. м. я. волновая ф-ция и вводитсяфеноменологич. эффективное взаимодействие между нуклонами в ядре, к-роеотличается от взаимодействия двух свободных нуклонов (в частности, оносильно зависит от плотности). Этот метод позволил количественно описатьсвойства ядер (энергии связи, радиусы и т. п.). В нём меньше "подгопочных"параметров, т. к. ср. поле, к-рое в О. м. я. задаётся независимо от остаточноговзаимодействия, здесь рассчитывается.
Ключ к пониманию О. м. я., а также методаХартри - Фока с эфф. силами дают теория ферми-жидкости Ландау и построепнаяна её принципах теория конечных ферми-системы (ТКФС) [3]. Основа этих теорий- концепция квазичастиц, согласно к-poй в ферми-системе с сильным взаимодействиеммежду частицами существует ветвь одночастичных фермионных возбуждений -квазпчастиц, движущихся и ср. поле, создаваемом др. частицами. Если энергияквазичастичного возбуждения невелика, то оно может жить достаточно долго:вероятность испытать неупругое столкновение мала из-за действия принципаПаули, резко ограничивающего число допустимых конечных состояний. Свойстватаких возбуждений похожи на свойства возбуждения газа невзаимодействующихфермионов, помещённых в потенциальную яму. Так, спин их равен ¹/₂,заряды по отношению к электрич. полю равны е для протонной квазичастицыи 0 - для нейтронной. Все эти утверждения следуют из точных законов сохранения.
Квазичастицы взаимодействуют между собой. В большинстве случаев можно ограничиться парным взаимодействием квазичастиц, к-рое эффективно учитывает и многочастичные взаимодействия частиц и поэтомуотличается от взаимодействия свободных нуклонов. В теории ферми-жидкостиколлективные возбуждения системы описываются в терминах этого эфф. взаимодействияс помощью ур-ния, учитывающего явно только двухчастичные корреляции и поформе совпадающего с ур-нием приближения случайных фаз. Именно возможностьограничиться двухчастичными корреляциями обусловливает выигрыш при переходеот частиц к квазичастицам.
В теории конечных ферми-систем эфф. взаимодействиеквазичастиц предполагается универсальным для всех ядер и задаётся феноменологически. Использование ур-ний ферми-жидкостного типа (см. Квантовая жидкость )позволилоописать не только коллективные возбуждения чётных ядер, но также статич. электрич. и магн. мультипольные моменты, вероятности эл.-магн. и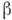 -переходовв нечётных ядрах и мн. др. ядерные характеристики.
Концепция квазичастиц оказалась плодотворнойи при описании глобальных ядерных свойств: анергий связи, плотностей, самосогласов. поля. Была сформулирована самосогласов. ТКФС, по своим возможностям совпадающаяс методом Хартри - Фока с эфф. силами, но более последовательная [4]. Используемоеэфф. взаимодействие квазичастиц зависит от их энергий и скоростей. Поэтомуи ср. поле, действующее на квазичастицу, также зависит от её энергии искорости [4]. Квазичастичные волновые ф-ции подчиняются ур-нию, подобномуур-шпо Шрёдингера с зависящей от координат эфф. массой т*(r). Эфф. массы нейтронов и протонов в ядре очень близки к массам свободных нуклонов. О. м. я. сыграла важную роль в развитии ядерной физики и в создании современныхмикроскопич. подходов в теории ядра.

Лит.:1) Гепперт-Майер М., ИенсенИ., Элементарная теория ядерных оболочек, пер. с англ., М., 1958; 2) БорО., Моттельсон В., Структура атомного ядра, пер. с англ., т. 1 - 2, М.,1971 - 77; 3) Мигдал А. В., Теория конечных ферми-систем и свойства атомныхядер, 2 изд., М., 1983; 4) Кhоdе1 V. A., Sареrstein Е. Е., Finite Fermisystems theory and self-consistency relations, "Pliys. Repts", 1982, v.,92,№5, p. 183.

Э. Е. Саперштейп.