Akademik

- сложное, нерегулярное (апериодическое) изменение состояния физ. системы в пространстве и/или во времени.

Происхождение хаотического поведения может быть обусловлено разл. причинами.

X. может представлять собой нек-рое многопериодическое движение:

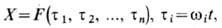
где F-2p-периодическая ф-ция по каждому аргументу. Тогда если среди частот w_i есть несоизмеримые, то реализация представляет сложное изменение со временем вектора состояния X. С возникновением многопериодических движений связан сценарий появления турбулентности по Ландау - Хопфу. В фазовом пространстве n -периодиче-ское движение описывается траекторией, наматывающейся на n -мерный тор. В частном случае n -торы образуются в результате сложения (суперпозиции) конечного числа гармонических колебаний. Напр., автономная система двух связанных осцилляторов, описываемая ур-ниями

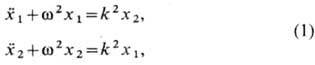
совершает двухпериодическое движение:

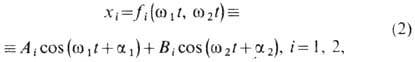
где А₁= А₂, В₁=-В₂,w²₁= w² - k²,w²₂=w² + k²,a₁ a₂ -нач. фазы. Если частоты w₁ и w₂ действительные и несоизмеримые, то соответствующее движение в общем случае апериодическое.

Сложная динамика может возникать также за счёт того, что под действием внеш. факторов параметры системы меняются со временем. Примером является неавтономная система, описываемая у р а в н е н и е м М а т ь ё:

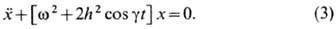
В областях стабильности (за исключением дискретного множества точек) величина х ограничена и меняется апериодически. В соответствии с теоремой Флоке - Ляпунова (иногда называемой Блоха теоремой )эта величина является двухпериодической ф-цией.

X. возникает, если в системе протекают случайные процессы. Такие процессы могут быть связаны со случайными внеш. воздействиями, а также с флуктуациями внутр. параметров. Примером случайного, хаотического процесса является броуновское движение. Динамика случайных процессов описывается ур-ниями для физ. характеристик - координат, скоростей и др., включающими случайные параметры (ур-ниями Ланжевена), а также ур-ниями для вероятностных характеристик системы. Напр., если процесс марковский, то при определ. допущениях эволюция ф-ции распределения f случайной величины и определяется из ур-ния Фоккера- Планка - Колмогорова:

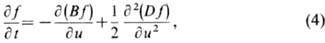
в к-ром В и D - интегральные моменты вероятности перехода системы между разл. допустимыми состояниями.

Случайный процесс характеризуется такими параметрами, как среднее, дисперсия, корреляц. ф-ция, спектральная ф-ция. Важным признаком случайности процесса является убывание корреляций по мере увеличения интервала времени между сопоставляемыми наблюдениями:

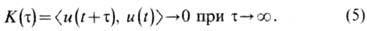
Этому условию не удовлетворяют, вообще говоря, многопериодические движения, подобные тем, к-рые описываются ур-ниями (1), (3). Кроме того, спектральный анализ таких движений выявляет наличие лишь конечного числа несоизмеримых частот и/или счётного (или конечного) чис-ла кратных частот. Поэтому многопериодические движения и колебания линейных неавтономных систем (если, конечно, внеш. "силы" не меняются стохастически) не обладают необходимыми свойствами истинно стохастических колебаний и по отношению к ним термины "хаотический" и "стохастический" употребляются редко.

Сложное поведение, обладающее основными свойствами случайного процесса, обнаруживается у мн. нелинейных динамических систем (т. н. хаос динамический). Качественно происхождение X. в таких системах связывают с тем, что нелинейные системы можно рассматривать как совокупность неск. взаимодействующих подсистем, обладающих разл. динамическими свойствами. Хаотическая динамика возникает в результате разл. рода процессов синхронизации колебаний указанных подсистем.

Наконец, в квантовых системах, описываемых линейным ур-нием Шрёдингера, стохастические колебания, вообще говоря, невозможны. Однако если характерные времена переходных процессов велики, может наблюдаться явление квантового X. Возможность подобного режима легко понять из того, что в классическом пределе система будет описываться нелинейными ур-ниями движения, для к-рых такая динамика известна (см. выше).

Лит.: Заславский Г. М., Стохастичность динамических систем, М., 1984; Рабинович М. И., Трубецков Д. И., Введение в теорию колебаний и волн, 2 изд., М., 1992; Гардинер К. В., Стохастические методы в естественных науках, пер. с англ., М., 1986; Неймарк Ю. И., Ланда П. С., Стохастические и хаотические колебания, М., 1987. Н. А. Кириченко.