Akademik

TURBINES À VAPEUR

Les turbines à vapeur, comme toutes les turbomachines (et contrairement aux machines volumétriques), sont des appareils à écoulement continu, ce qui veut dire que, pour un régime de fonctionnement donné, l’état du fluide est invariable en tout point. Cette propriété leur permet de fonctionner avec des débits très importants et rend donc possible la réalisation de machines de grande puissance (pouvant dépasser un million de kilowatts), et cela avec un rendement élevé et avec toute la souplesse de réglage exigée par le fonctionnement des centrales électriques modernes. De plus, les turbines à vapeur se prêtent, dans des conditions économiques, à la production simultanée d’énergie électrique et de chaleur. Pour toutes ces raisons, ces machines jouent un rôle de tout premier plan dans la production d’énergie électrique aux dépens de la chaleur fournie par les combustibles, qu’ils soient classiques ou nucléaires.

1. Principe de fonctionnement et classification

Une turbine à vapeur comporte un ou plusieurs étages , composés chacun de deux aubages , ou grilles d’aubes, dont l’un est fixe et l’autre mobile. Le plus souvent, la direction générale de l’écoulement de la vapeur est parallèle à l’axe de la turbine; celle-ci est alors du type axial . Dans certains cas, cette direction est perpendiculaire à l’axe (habituellement, dans le sens centripète); la turbine est alors du type radial .

La figure 1 représente une coupe longitudinale partielle d’une turbine axiale. La vapeur se détend dans les aubages fixes (1), qui sont montés sur des diaphragmes (3); toutefois, pour l’aubage fixe du premier étage (qui n’est pas représenté dans la figure), des dispositions spéciales facilitent l’admission de vapeur et le réglage de la turbine. Chacun des aubages fixes est suivi d’un aubage mobile (2) monté sur un disque (4); les différents disques sont fixés sur l’arbre (5), qui transmet la puissance développée par la turbine à l’appareil entraîné par celle-ci (par exemple, à une génératrice électrique). Pour réduire les fuites de vapeur entre la partie centrale des diaphragmes et les moyeux des disques, on munit les diaphragmes de lamelles métalliques (6) dont l’ensemble forme un labyrinthe.

En développant les aubages fixe et mobile d’un étage dans un plan, on obtient la disposition représentée sur la figure 2, (A) étant l’aubage fixe et (B) l’aubage mobile.

Le fonctionnement d’un étage de turbine peut être conçu de deux manières Dans le premier cas, toute la détente a lieu dans l’aubage fixe, le rôle de l’aubage mobile étant d’utiliser l’énergie cinétique engendrée par cette détente; c’est le cas d’un étage à action . Dans le second, la vapeur ne se détend que partiellement dans l’aubage fixe, le reste de la détente ayant lieu dans l’aubage mobile; ce mode de fonctionnement caractérise l’étage à réaction . On a donc, dans le premier cas, p ⁰ 礪 p ¹ = p ² et, dans le second, p ⁰ 礪 p ¹ 礪 p ², où p ⁰ est la pression à l’amont de l’aubage fixe, p ¹ la pression entre les aubages fixe et mobile, et p ² la pression à l’aval de l’aubage mobile. Le mode de construction représenté sur la figure 1 est celui d’une turbine à action; dans le cas d’une turbine à réaction, afin de réduire la poussée axiale due à l’inégalité des pressions régnant de part et d’autre des aubages mobiles, on monte ceux-ci non pas sur des disques, mais sur un tambour. Cette disposition est représentée sur la figure 3: les aubages fixes (1) sont montés à l’intérieur d’un stator (2), tandis que les aubages mobiles (3) sont fixés sur un tambour (4), monté sur l’arbre de la turbine (ce tambour peut d’ailleurs être constitué par des disques soudés entre eux).

Lorsque le nombre d’étages d’une turbine est très grand, on répartit la détente totale entre plusieurs turbines placées en série, les arbres de ces turbines étant reliés entre eux au moyen d’accouplements; on dit alors que la turbine comporte plusieurs corps, et on désigne ceux-ci par le niveau de pression correspondant: par exemple, corps H.P., corps M.P., corps B.P. (respectivement, haute, moyenne et basse pression).

Si le débit-volume traversant un corps de turbine est élevé, ce corps peut comporter plusieurs flux parallèles. Cette disposition s’applique surtout aux corps B.P. où le volume massique de la vapeur atteint des valeurs très élevées: dans certains cas, la turbine comporte trois ou même quatre corps B.P. à deux flux chacun, ce qui conduit à six ou à huit échappements de vapeur.

Enfin, suivant le cycle thermique décrit par la vapeur, on distingue, entre autres, les turbines à condensation, à contre-pression, à prélèvement de vapeur.

2. Écoulement de la vapeur

Comme la vapeur traverse la turbine à une vitesse de l’ordre de plusieurs centaines de mètres par seconde, la durée de son séjour est très réduite, de sorte que les échanges de chaleur entre la vapeur et les parois sont négligeables; par conséquent, l’écoulement de la vapeur peut être considéré comme adiabatique. Si, de plus, la turbine est supposée parfaite, l’écoulement est réversible et la transformation décrite par la vapeur est alors isentropique; en assimilant la vapeur à un gaz parfait, elle peut être exprimée par la relation:

où c ^p et c ^v sont respectivement les chaleurs massiques de la vapeur à pression constante ^{[cf. THERMODYNAMIQUE]}.

Désignons la pression et le volume massique de la vapeur au début de la détente par p ⁰ et v⁰, à la fin de celle-ci, par p ¹ et v¹. La détente a lieu dans un canal approprié constitué en fait par l’espace compris entre deux aubes fixes; la vitesse à l’amont de ce canal étant supposée nulle, la vitesse à l’aval c est donnée par la relation:

ou par la relation équivalente:

où H est la variation d’enthalpie de la vapeur au cours de la détente. Si l’enthalpie H est exprimée en joules par kilogramme, la vitesse est en mètres par seconde. Si le débit-masse de vapeur est de 1 kilogramme par seconde, on évalue chacune des sections du canal normales à la vitesse c par l’expression:

Or, la relation entre le rapport v/c et le rapport m = p ¹/p ⁰ passe par un minimum; la valeur correspondante de m est le taux de détente critique m ^c donné par:

En introduisant m ^c dans (2), on obtient l’expression de la vitesse critique c ^c :

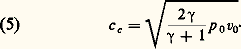
Quant aux valeurs correspondantes de la température et du volume massique, elles sont respectivement:

Les relations (5) et (7) permettent de trouver la valeur de la section de passage S^c lors de la détente critique d’un débit de vapeur égal à 1 kilogramme par seconde; l’inverse de cette section, soit:

est le débit critique (en kilogrammes par seconde) correspondant à une section de passage de 1 mètre carré.

Le rapport 塚 = c ^p /c ^v varie, dans une certaine mesure, avec l’état de la vapeur; les valeurs de 塚 et de m ^c figurant dans le tableau ci-dessous ne sont donc qu’approximatives. Les résultats obtenus montrent que, si p ¹/p ⁰ 閭 m ^c , la détente doit avoir lieu dans un canal convergent ; mais, si p ¹/p ⁰ 麗 m ^c , la section du canal passe par un minimum, de sorte que le canal comporte une partie convergente, un «col» (correspondant à la section minimale) et une partie divergente.

3. Étude d’un étage de turbine à action

L’état de la vapeur à l’amont de l’aubage fixe (fig. 4) est défini par les valeurs de la pression p ⁰ et de la température ⁰; le diagramme H,S permet detrouver la variation d’enthalpie H entre cet état initial et la pression p ¹ = p ², qui règne à l’aval du même aubage. La vitesse de la vapeur c ¹ à la sortie de l’aubage fixe est alors donnée par la relation (3); quant à la direction de cette vitesse, elle est définie par l’angle 見¹ entre le bord de sortie de l’aubage A et le plan frontal (c’est-à-dire le plan perpendiculaire à l’axe de la turbine).

La connaissance de l’état de la vapeur à la fin de la détente fournit la valeur du volume massique v¹ à la sortie de l’aubage fixe. Pour un débit-masse donné q ^m , le débit-volume dans la section de sortie de l’aubage A est donc: q ^v = q ^m v¹ et, par conséquent, la section de passage devant être offerte à la vapeur est:

Cette section doit évidemment être mesurée perpendiculairement à la direction de la vitesse c ¹; en désignant par D^moy le diamètre moyen de l’aubage, et par h ¹ la longueur (dimension radiale) de celui-ci, on obtient la relation:

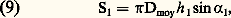
qui donne la valeur de h ¹ pour des valeurs données de S¹, D^moy et 見¹.

Pour une vitesse de rotation donnée N (en tours par seconde), la vitesse circonférentielle u au diamètre moyen de l’étage a la valeur u = 神D^moyN. Cette vitesse est représentée, sur la figure 5, par un vecteur qui, comme le vecteur c ¹, est l’un des côtés du triangle des vitesses à l’entrée de l’aubage mobile; le troisième côté représente, en grandeur et en direction, la vitesse relative w ¹ de la vapeur par rapport à cet aubage. Pour éviter un choc du jet de vapeur contre les parois des aubes mobiles, celles-ci doivent former avec le front de grille un angle 廓¹ égal à celui qui est formé par les vecteurs u ¹ et w ¹.

Dans des conditions idéales, l’écoulement dans l’aubage mobile n’est accompagné d’aucune perte par frottement, ce qui conduit à l’égalité: w ¹ = w ², w ² étant la vitesse relative de la vapeur à la sortie des aubes mobiles. Si, de plus, les aubes fixes et mobiles ont la même longueur h ¹ = h ², les angles 廓¹ et 廓² (fig. 5) sont égaux; les aubes mobiles ont, dans ces conditions, un profil ayant un axe de symétrie. La connaissance des vecteurs u et w permet de construire le triangle des vitesses à la sortie de l’aubage mobile; le troisième côté de ce triangle représente, en grandeur et en direction, la vitesse absolue c ² de la vapeur à la sortie de cet aubage.

4. Puissance et rendement

L’application à l’étage de turbine de la loi de la conservation de l’énergie donne:

Pour un débit-masse q ^m , exprimé en kilogrammes par seconde, la puissance fournie par la vapeur dans l’étage considéré est par conséquent (exprimée en watts):

Or, l’examen des triangles des vitesses correspondant à l’entrée et à la sortie de l’aubage mobile permet d’établir la relation:

où la grandeur c ^u , qui est la variation dans l’aubage mobile de la composante tangentielle (c ^u ) de la vitesse absolue de la vapeur, est donnée immédiatement par l’épure des vitesses (fig. 5) qu’on obtient en superposant les deux triangles construits précédemment.

L’expression du rendement est donnée par:

Pour un angle 見¹ donné, 兀 ne dépend donc que du rapport 﨡 = u /c ¹; on obtient ainsi:

ou, en tenant compte de (13):

Il en résulte que le rendement passe par un maximum pour une valeur de 﨡, qui est:

la valeur maximale du rendement étant:

Ce raisonnement ne tient pas compte des pertes qui accompagnent l’écoulement de la vapeur dans les aubages fixe et mobile. L’intervention de ces pertes entraîne évidemment une certaine réduction du rendement, mais elle laisse inchangée l’expression (16) de 﨡^opt; comme l’angle 見¹ est habituellement petit, la valeur de 﨡^opt, pour un étage à action, est légèrement inférieure à 0,5.

5. Étage de turbine à réaction

L’inégalité p ¹ 礪 p ², qui caractérise le fonctionnement d’un étage à réaction, permet de représenter la variation d’enthalpie H dans celui-ci sous la forme:

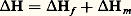
où H^f et H^m sont respectivement les variations d’enthalpie dans l’aubage fixe et dans l’aubage mobile. Le rapport:

est, par définition, le degré de réaction de l’étage; pour un étage à action, comme H^m = 0, on a évidemment 靖 = 0.

La construction du triangle des vitesses à l’entrée de l’aubage mobile peut être réalisée comme suit. Supposons que l’étage considéré soit précédé d’un autre étage à réaction et que la vitesse absolue c ² conserve la même valeur en passant d’un étage au suivant. Pour l’étage étudié, la vitesse c ¹ sera alors:

et la combinaison de c ¹ et de u permet de trouver, comme dans le cas d’un étage à action, la vitesse relative w ¹ à l’entrée de l’aubage mobile. Quant au triangle des vitesses à la sortie de cet aubage, il peut être obtenu en utilisant la relation:

Le cas le plus simple est celui d’un étage (supposé parfait) dont les dimensions radiales varient de manière à obtenir la même valeur de la composante axiale de la vitesse de la vapeur à la sortie de l’aubage fixe et à la sortie de l’aubage mobile. Si, de plus, 靖 = 0,5, les aubages fixe et mobile sont symétriques et les deux triangles ont la forme représentée sur la figure 6. La condition du rendement maximal peut être exprimée en fonction du rapport 﨡 = u /c , où c est une vitesse fictive correspondant à la variation totale d’enthalpie de l’étage:

Il est facile de vérifier que, dans ces conditions, l’examen des triangles de la figure 6 conduit à la relation:

La comparaison de (16) et de (19) montre que, pour une vitesse circonférentielle u donnée, la valeur optimale de H est, pour un étage à réaction (avec 靖 = 0,5), deux fois

plus petite que pour un étage à action, de sorte que, pour des conditions de fonctionnement données, le nombre d’étages est deux fois plus grand dans le cas d’une turbine à réaction que dans celui d’une turbine à action. En revanche, la construction des aubes est plus simple dans le premier cas que dans le second.

6. Réglage

Le réglage d’une turbine à vapeur a pour but de maintenir constante une certaine grandeur qui dépend de la nature de l’appareil entraîné: vitesse de rotation si cet appareil est une génératrice de courant alternatif, pression ou débit si cet appareil est un compresseur ou une pompe. Dans tous les cas, l’action du dispositif de réglage se traduit par une adaptation de la puissance développée à la valeur instantanée de la puissance demandée, cette adaptation étant réalisée en agissant sur le débit-masse de vapeur admis.

À cet effet, on munit la turbine d’une soupape de réglage soumise à l’action d’un régulateur (qui, dans le cas d’un groupe électrogène, est un régulateur centrifuge) et dont la position détermine le débit de vapeur admis.

Le débit-masse passant dans le premier aubage fixe est à peu près proportionnel à la pression régnant à l’amont de cet aubage, donc à l’aval de la soupape; d’autre part, la pression à l’amont de la soupape est, aux pertes de charge près, celle de la chaudière, et, par conséquent, elle est pratiquement constante. Une fermeture partielle de la soupape de réglage provoque une baisse de pression et entraîne une réduction simultanée du débit-masse et de la différence d’enthalpie disponible dans la turbine: c’est le réglage par laminage de vapeur .

Ce mode de réglage a pour effet une baisse de rendement aux charges réduites. Pour atténuer cet inconvénient, on divise le premier aubage fixe en plusieurs secteurs séparés par des cloisons et alimentés par des soupapes de réglage s’ouvrant successivement. À la pleine ouverture de chaque soupape correspond ainsi un régime de fonctionnement sans laminage de vapeur, celui-ci n’intervenant que pour les régimes où l’une des soupapes n’est ouverte que partiellement: c’est le réglage par injection partielle . Son emploi exige toutefois que l’étage de tête de la turbine soit à action et non à réaction.

Pour une turbine à condensation, dans les limites de l’action de chaque soupape, la variation du débit-masse de vapeur avec la puissance développée P est pratiquement linéaire. Sur la figure 7, la droite A représente cette variation dans le cas d’un réglage par laminage (donc, d’une seule soupape de réglage), et la lignée brisée B correspond au cas de trois soupapes de réglage s’ouvrant successivement. Des soupapes supplémentaires peuvent également être prévues pour permettre à la turbine de fonctionner en surcharge , c’est-à-dire de fournir une puissance supérieure à sa puissance nominale. Le débit supplémentaire traversant les soupapes de surcharge peut être admis soit dans le premier étage de la turbine, soit dans un étage intermédiaire de celle-ci; cette dernière solution permet d’adopter pour le premier étage un fonctionnement sans surcharge à injection totale, tandis que la première implique, pour cet étage, une injection partielle. Dans tous les cas, le fonctionnement en surcharge entraîne une légère baisse du rendement de la turbine.