Akademik

POMPAGE OPTIQUE

Le pompage optique est un procédé qui permet de changer d’une manière appréciable les valeurs des populations des états quantifiés des atomes, des molécules et des ions (on désigne par le mot «population» le nombre d’atomes dans un état quantique donné). On peut ainsi créer une distribution de population très différente de la distribution d’équilibre thermique et maintenir un état permanent de cette nouvelle distribution. En irradiant une assemblée d’atomes avec une lumière monochromatique dont la fréquence correspond à une raie d’absorption de l’atome à partir de l’état fondamental (raie de résonance), on peut peupler un niveau excité donné et changer la répartition de population entre les états de structure hyperfine et les états Zeeman de l’état fondamental. On est amené à employer une radiation incidente convenablement polarisée pour modifier la population des états Zeeman.

Dans cet article, après avoir rappelé quelques notions fondamentales relatives aux niveaux d’énergie des atomes (cf. optique QUANTIQUE), on s’intéressera au mécanisme du pompage optique dans le cas particulier de l’atome de sodium, et on rappellera les applications des techniques du pompage optique aux différents domaines de la physique, en renvoyant, pour plus de précisions, le lecteur aux articles LASERS et HORLOGES ATOMIQUES.

1. Répartition entre niveaux d’énergie

L’état énergétique d’une assemblée comprenant un grand nombre d’atomes identiques peut être caractérisé par leur répartition entre les différents niveaux d’énergie ^{[cf. ATOME]}: N¹ est le nombre des atomes qui se trouvent à l’état E¹, et, d’une façon générale, Nⁿ est le nombre d’atomes dans un état d’énergie Eⁿ . On dit que Nⁿ est la population de l’état Eⁿ .

Lorsque le milieu auquel appartiennent les atomes est à l’état d’équilibre thermique à une température donnée T, les populations Nⁿ des différents états Eⁿ obéissent à la loi de Boltzmann, soit Nⁿ proportionnel à exp(face=F0019 漣 Eⁿ /k T), où k est la constante de Boltzmann égale au quotient de la constante R des gaz parfaits par le nombre d’Avogadro 類:

(la constante k a les dimensions d’une énergie divisée par une température; elle est ici exprimée en joule par kelvin).

Plus l’état d’énergie est élevé (Eⁿ grand), plus la population correspondante Nⁿ est faible.

L’état d’énergie le plus bas, E¹, s’appelle l’«état fondamental de l’atome»; les autres états d’énergie s’appellent les «états excités». La relation de Boltzmann peut se mettre sous la forme:

Sous cette forme, elle permet de comparer directement la population d’un état excité Eⁿ à celle de l’état fondamental E¹.

Lorsque la différence d’énergie Eⁿ est très supérieure à k T (soit Eⁿ 礪礪 k T), la population Nⁿ est pratiquement négligeable par rapport à celle de l’état fondamental; en outre, lorsqu’il en est ainsi pour tous les états Eⁿ , tous les atomes se trouvent dans l’état fondamental à l’équilibre thermique, et les états excités sont vides.

Au contraire, quand il existe des états Eⁿ proches de l’état fondamental ( Eⁿ de l’ordre de k T), leur population est importante, et, dans le cas où Eⁿ 廉 k T, ils sont aussi peuplés que l’état fondamental.

Si une assemblée d’atomes est perturbée et mise dans un état différent de l’état d’équilibre thermique (par exemple, par une décharge électrique au sein du gaz ou par une irradiation optique), les processus de relaxation ont toujours tendance à rétablir l’état d’équilibre thermique. Lorsqu’ils interviennent seuls, le système se maintient à l’équilibre thermique.

En général, à un changement de structure électronique d’un atome par rapport à l’état fondamental correspond une variation d’énergie Eⁿ de l’ordre de plusieurs électrons-volts, grande par rapport à k T (1 eV = 1,602 憐 10 size=1^漣19 J), et les états excités correspondants sont complètement dépeuplés à la température ordinaire.

2. États Zeeman

Dans les atomes paramagnétiques qui possèdent, à l’état fondamental, un moment magnétique non nul, l’application d’un champ magnétique décompose l’état fondamental en plusieurs états voisins appelés «états Zeeman». Dans les champs magnétiques que l’on sait produire, les intervalles d’énergie entre ces états restent petits par rapport à k T, de sorte qu’à l’équilibre thermique, à la température ordinaire, tous les états Zeeman ont des populations pratiquement égales. Cela est vrai aussi pour les états Zeeman résultant d’un paramagnétisme nucléaire (lorsque les noyaux possèdent un faible moment magnétique).

Enfin, lorsqu’un atome possède à la fois du paramagnétisme d’origine électronique et du paramagnétisme d’origine nucléaire, l’interaction entre le moment magnétique électronique et le moment nucléaire produit une décomposition de l’état fondamental d’un atome en plusieurs états qu’on appelle les «états de structure hyperfine», et les intervalles d’énergie entre ces états sont faibles par rapport à k T. Les états électroniques excités possèdent en général aussi une structure hyperfine et ils peuvent se décomposer, dans un champ magnétique extérieur, en une suite d’états Zeeman.

Les divers états Zeeman d’un même état électronique se distinguent non seulement par de petites différences d’énergie mutuelles, mais aussi par l’orientation dans l’espace du vecteur moment magnétique de chaque atome. Pour un état Zeeman donné, ce moment magnétique fait un angle déterminé avec le champ magnétique appliqué, et cet angle varie de façon discontinue d’un état Zeeman à un autre.

Dans le cas simple où un état atomique se décompose en deux états Zeeman seulement, le moment magnétique des atomes est parallèle au champ dans l’un de ces états Zeeman et antiparallèle au champ dans l’autre. Cela est réalisé dans l’état fondamental de l’atome d’hydrogène et dans les états fondamentaux des atomes alcalins.

3. Exemple du sodium

États quantiques du sodium

Pour analyser le mécanisme du pompage optique, on va considérer l’exemple d’un atome alcalin, celui du sodium, en faisant abstraction de la complication de structure hyperfine qui est due à l’existence du spin et du moment magnétique nucléaire du ²³Na. Cette simplification est justifiée dans le cas où le champ magnétique appliqué est suffisamment fort pour produire des intervalles Zeeman qui sont grands par rapport aux intervalles de structure hyperfine.

L’état fondamental de l’atome de sodium est un état désigné par le symbole S1/2 par les spectroscopistes. Dans un tel état, le moment magnétique de l’atome, égal à un magnéton de Bohr, est dû au spin de l’électron de valence. Ce moment peut s’orienter soit dans le sens du champ magnétique, soit en sens opposé. Chacune de ces orientations correspond à un état Zeeman. L’état Zeeman pour lequel le moment magnétique est orienté dans le sens du champ possède l’énergie la plus basse et est noté: état m = 漣 1/2; l’état Zeeman pour lequel le moment magnétique est orienté en sens opposé à celui du champ est noté: m = + 1/2. L’intervalle d’énergie entre ces deux états m de l’état fondamental est proportionnel au champ magnétique appliqué.

Dans la vapeur de sodium, à température modérée (300 à 400 K), les deux états m = 漣 1/2 et m = + 1/2 possèdent sensiblement la même population: 50 p. 100 des atomes se trouvent dans l’un des états Zeeman et 50 p. 100 dans l’autre.

La vapeur de sodium absorbe très fortement la lumière jaune émise par une lampe à sodium. Cette lumière est composée de deux radiations monochromatiques D¹ et D², dont les nombres d’onde diffèrent de 17 cm size=1^漣1 et qu’on distingue aisément avec un bon spectroscope. L’absorption de la radiation D¹ porte l’atome de sodium de l’état fondamental S^1/2 à un état excité que les spectroscopistes désignent par le symbole P^1/2; l’absorption de la radiation D² porte l’atome à un état excité voisin appelé P^3/2. Dans un champ magnétique, l’état P^1/2 est décomposé en deux états Zeeman que l’on notera m = 漣 1/2 et m = + 1/2. L’intervalle d’énergie qui les sépare est trois fois plus petit que celui correspondant à l’état fondamental. L’autre état excité P^3/2 est décomposé par le champ magnétique en quatre états Zeeman équidistants.

Pour simplifier, on se bornera à étudier l’action sur la vapeur de sodium de la raie D¹.

Le schéma de la figure 1 indique la structure Zeeman des deux états S^1/2 et P^1/2 et montre que la raie D¹ se décompose en quatre composantes (composantes Zeeman ) qu’on désigne par les lettres a, b, c et d .

Ces quatre composantes ont des fréquences légèrement différentes (dans un champ de 10 000 G, l’écart entre les composantes extrêmes a et d n’est que de 1,3 cm size=1^漣1), mais elles se distinguent également par leur état de polarisation. Les deux composantes internes b et c sont polarisées rectilignement, le vecteur électrique de l’onde électromagnétique étant parallèle au champ magnétique (polarisation 神), tandis que les deux composantes externes a et d sont polarisées circulairement dans un plan perpendiculaire au champ. Leurs sens de circulation sont opposés: on dit que a possède la polarisation 靖 size=1^漣 et que d possède la polarisation 靖⁺. Ce dernier sens de circulation est celui du courant électrique dans les bobines de l’électro-aimant qui produit le champ.

Mécanisme du pompage optique

On peut tirer parti de ces différences de polarisation pour faire du pompage optique sélectif. En polarisant circulairement la lumière incidente de la lampe de sodium, conformément à 靖⁺, on isole dans la lumière excitatrice la composante Zeeman d de la raie D¹, et la figure montre que seuls les atomes qui sont à l’état fondamental dans l’état Zeeman m = 漣 1/2 peuvent absorber cette raie. Ils sont ainsi portés à l’état excité Zeeman correspondant à m = + 1/2. Par ce processus d’excitation, on peuple donc cet état à l’exclusion de l’état m = 漣 1/2. Tous les atomes ainsi excités ont leurs moments magnétiques orientés dans le même sens (dans ce cas, le sens opposé à celui du champ). À partir de l’état excité m = + 1/2, les atomes retombent à l’état fondamental par émission spontanée, la durée moyenne de séjour d’un atome dans l’état excité n’étant que de l’ordre de 10 size=1^漣8 s (durée de vie de l’état excité). Les atomes peuvent emprunter deux voies pour retourner à l’état fondamental, la voie d (la même qu’à la montée) ou la voie b . La première les ramène à l’état de départ m = 漣 1/2, mais la seconde les fait transiter vers l’état m = + 1/2 de l’état fondamental. La théorie indique que le choix de la voie d est deux fois plus probable que celui de la voie b . De trois atomes qui ont subi l’excitation à partir de l’état m = 漣 1/2, deux retournent à cet état, mais le troisième transite vers l’état m = + 1/2. Si, avant illumination, la vapeur de sodium contient 100 atomes à l’état fondamental, 50 dans chacun des deux états Zeeman, et si on illumine ces atomes avec la composante d de la raie D¹ pendant un temps suffisant pour que 30 des atomes à l’état m = 漣 1/2 soient excités, 20 autres n’ayant pas subi l’excitation, on aura 20 + 20 = 40 atomes à l’état m = 漣 1/2 et 50 + 10 = 60 à l’état m = + 1/2, après retour à l’état fondamental.

Degré d’orientation

On peut illuminer une nouvelle fois la vapeur pour exciter de nouveau 30 des 40 atomes qui sont à l’état m = 漣 1/2 (à intensité lumineuse égale, il faudra maintenant, pour obtenir cet effet, une durée d’illumination plus longue, car le nombre d’atomes excitables a diminué). Après cette deuxième étape d’excitation, il y aura 10 + 20 = 30 atomes à l’état m = 漣 1/2 et 60 + 10 = 70 atomes à l’état m = + 1/2, et ainsi de suite.

On a l’habitude de caractériser cette modification de population par le degré d’orientation qui est défini de la façon suivante:

^+1/2 étant le nombre d’atomes à l’état m = + 1/2 et N size=1^漣1/2 le nombre d’atomes à l’état m = 漣 1/2.

Dans l’exemple choisi, le degré d’orientation avant illumination est nul; après les deux étapes d’illumination, il a atteint la valeur:

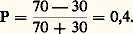
Si l’on poursuit l’illumination, P continue à grandir. Sa valeur maximale (P = 1) correspond à l’orientation complète: N^+1/2 = 100 et N 漣1/2 = 0.

En réalité, même avec une illumination intense et permanente, on n’atteint pas la limite P = 1, car le processus de pompage par la lumière est contrarié par le processus appelé «processus de relaxation», qui tend à ramener les populations des deux états Zeeman à leurs valeurs d’équilibre thermique, processus qui, selon les conditions expérimentales, est plus ou moins rapide.

Conditions optimales de pompage

Lorsque l’illumination qui produit le pompage optique est maintenue en permanence, un état d’équilibre dynamique s’établit au cours duquel le processus de pompage est compensé par le processus de relaxation. Le degré d’orientation qui correspond à cet état stationnaire est d’autant plus élevé que la vitesse de pompage est plus grande et que la vitesse de relaxation est plus faible.

De nombreuses études expérimentales ont été faites pour agir sur ces deux facteurs afin d’obtenir les conditions optimales de pompage.

La vitesse de pompage optique dépend de l’intensité lumineuse de la lampe spectrale qui éclaire les atomes, mais cette vitesse ne croît pas proportionnellement à l’intensité de cette lampe lorsqu’on augmente la puissance d’alimentation de celle-ci. La raie d’absorption de la vapeur est très fine et seule la lumière de la lampe à l’intérieur d’une bande spectrale très étroite est efficace. Lorsqu’on élève la puissance d’alimentation d’une lampe à décharge, l’intensité totale des raies augmente, mais en même temps ces raies s’élargissent.

Les meilleures sources lumineuses, au point de vue du rendement de pompage optique, sont des lampes sans électrodes contenant un peu de métal pur, sous une pression d’argon de quelques millimètres de mercure, excité en haute fréquence par le rayonnement d’un magnétron dont l’antenne rayonnante doit être convenablement adaptée.

Le deuxième facteur sur lequel il faut agir pour atteindre les conditions optimales est la vitesse de relaxation . Lorsqu’on supprime brusquement le faisceau lumineux, on constate que le degré P décroît suivant une loi exponentielle P = P⁰e ^{t /} size=1^精. Au bout du temps t = 精, la polarisation est réduite à 1/e de sa valeur. Cette durée caractéristique 精 s’appelle le temps de relaxation .

Temps de relaxation

Dans une vapeur orientée optiquement, la relaxation est due aux chocs que subissent les atomes. Aux très faibles densités de vapeur auxquelles on opère en utilisant les vapeurs alcalines, le libre parcours moyen des atomes est grand; et, en l’absence de gaz étrangers, les chocs entre atomes sont négligeables. Seuls entrent en ligne de compte les chocs des atomes contre les parois du récipient (cf. théorie CINÉTIQUE DES FLUIDES). La vapeur de sodium devant être soumise au pompage optique, la paroi doit être transparente; on choisit donc une paroi en verre. L’expérience montre que, pour une cellule sphérique dont les dimensions sont de quelques centimètres, le temps de relaxation 精 est de l’ordre de 10⁴ s, ce qui correspond pratiquement au temps de déplacement des atomes entre les parois. La brièveté de ce temps de relaxation limite sévèrement le degré d’orientation qu’on peut atteindre en régime permanent d’illumination, et l’on a cherché des moyens pour allonger 精. Deux procédés permettent d’obtenir un tel résultat: l’addition d’un gaz noble et l’enduit des parois de la cellule.

L’addition d’un gaz étranger, et en particulier celle d’un gaz noble (hélium, argon, etc.), un tel gaz jouant le rôle de gaz tampon (les auteurs anglo-saxons disent buffer-gas ), protège les atomes alcalins contre les chocs sur les parois. Or, un gaz étranger ne peut jouer le rôle de gaz protecteur que si les chocs entre une molécule étrangère et un atome alcalin ne sont pas relaxants. En réalité, ces chocs produisent aussi une relaxation, mais celle-ci est extrêmement lente, en particulier dans l’hélium: sous une pression de plusieurs centimètres de mercure, on a mesuré des temps de relaxation 精 qui atteignent l’ordre de grandeur de la seconde.

La deuxième méthode qui permet d’allonger le temps de relaxation 精 consiste à recouvrir les parois de la cellule d’un enduit mince de paraffine ou de silicone. Dans le cas de vapeur de rubidium, une étude systématique de ces enduits a été faite au laboratoire de physique de l’École normale supérieure à Paris par J. Brossel et M. A. Bouchiat, qui ont montré que les enduits de paraffine deutérée sont particulièrement efficaces.

Mesure des degrés d’orientation

Il ne suffit pas de pouvoir atteindre par pompage optique des degrés d’orientation élevés, il faut encore savoir mesurer ces degrés. L’examen du schéma de la figure 1 montre que seuls les atomes à l’état Zeeman m = 漣 1/2 sont susceptibles d’absorber la composante d polarisée en 靖⁺ de la radiation pompante D¹.

Au fur et à mesure que le pompage optique progresse, le nombre d’atomes à l’état m = 漣 1/2 diminue au bénéfice de l’état m = + 1/2. Le coefficient d’absorption de la vapeur pour la raie D¹ polarisée circulairement en 靖⁺ va donc diminuer: pendant le processus de pompage, la vapeur devient plus transparente. Il suffit donc de disposer, à la suite de la cellule à vapeur alcaline, un détecteur photoélectrique qui mesure l’intensité de la lumière ayant traversé la vapeur. Le signal augmente au cours du processus de pompage.

La figure 2 donne l’intensité lumineuse I du faisceau pompant qui traverse la cellule de résonance, en fonction de temps t , pour de la vapeur de rubidium. Elle montre qu’au cours du pompage optique la transparence de la vapeur augmente.

4. Applications

La méthode de pompage optique qui permet de changer les répartitions de population entre les états Zeeman ou entre les états de structure hyperfine d’un atome en phase vapeur fait l’objet de nombreuses applications.

Toute cause qui produit une modification du degré d’orientation est susceptible d’être étudiée. Il devient ainsi possible de faire, dans les différents cas, une étude détaillée des processus de relaxation.

Un procédé efficace pour changer les répartitions de population des états atomiques est la résonance magnétique . Elle consiste à appliquer aux atomes un champ magnétique de haute fréquence. Lorsque la fréquence 益 de ce champ est accordée à un intervalle d’énergie E entre deux états atomiques (deux états Zeeman ou deux états hyperfins), c’est-à-dire lorsque cette fréquence satisfait à la condition de Bohr:

où h est la constante de Planck, le champ de haute fréquence induit des transitions qui ont pour effet d’égaliser les populations des deux états Eⁱ et E^j en question.

Cette modification de population affecte la transparence de la vapeur, ce qui permet de détecter la résonance lorsqu’on fait varier la fréquence du champ alternatif. On peut ainsi mesurer avec précision les fréquences de résonance des atomes et en déduire les intervalles E entre deux niveaux d’énergie.

On a vu que les techniques de pompage optique permettent d’orienter les moments magnétiques des électrons de valence des atomes alcalins. On peut les utiliser aussi pour orienter de façon analogue les moments magnétiques des noyaux atomiques et s’en servir pour mesurer des temps de relaxation nucléaire et pour déterminer les fréquences de résonance magnétique nucléaire. C’est ce qui a été fait au laboratoire de physique de l’École normale supérieure à Paris par B. Cagnac pour les noyaux des deux isotopes impairs de la vapeur de mercure ¹⁹⁹Hg et ²⁰¹Hg.

La figure 3 montre des courbes de résonance magnétique nucléaire obtenues par B. Cagnac sur le mercure 199. Chaque courbe correspond à une amplitude constante du champ de radiofréquence appliqué dont on fait varier la fréquence, le champ magnétique appliqué, de l’ordre de 253 G, étant maintenu constant. Grâce à l’extension de cette méthode, de nombreux moments magnétiques nucléaires ont été déterminés avec une grande précision. Ainsi la valeur pour le ¹⁹⁹Hg a été trouvée égale à 0,497 865 magnéton nucléaire.

Une application importante des techniques de pompage optique en physique atomique fondamentale est la mise en évidence d’interactions fines entre le rayonnement et les atomes, interactions prévues par J. P. Barrat et C. Cohen-Tannoudji et expérimentalement étudiées par ce dernier et ses collaborateurs. Des radiations électromagnétiques soit du domaine des radiofréquences, soit du domaine optique, dont les fréquences ne sont pas des fréquences de résonance de l’atome, provoquent des transitions, appelées «transitions virtuelles», qui sont susceptibles de modifier profondément les propriétés des atomes, de déplacer leurs niveaux d’énergie et d’altérer le moment magnétique atomique. Il est ainsi possible de produire un dédoublement Zeeman grâce à un faisceau lumineux en absence de tout champ magnétique, ou au contraire de supprimer l’effet Zeeman malgré la présence d’un champ magnétique constant. Ces recherches ont conduit Cohen-Tannoudji à introduire le concept d’atome habillé (cf. Bibliographie ).

Certains des intervalles entre états Zeeman sont sensiblement proportionnels au champ magnétique constant qui agit sur les atomes. Une mesure de fréquence constitue donc une mesure de champ. On utilise ainsi le pompage optique pour la construction de magnétomètres qui permettent notamment l’exploration du champ magnétique terrestre. D’autres fréquences de résonance, en particulier celles qui correspondent aux intervalles hyperfins, sont des caractéristiques de l’atome étudié. Comme ces fréquences sont susceptibles d’être mesurées avec une précision relative de l’ordre de 10¹¹ à 10¹², on peut les utiliser comme fréquences étalons et leur comparer d’autres fréquences de mouvements périodiques, celles des horloges à quartz, des pendules de gravitation, de la Terre en rotation. On est ainsi amené à définir l’unité de temps par des horloges atomiques telle celle qui est fondée sur la mesure de fréquence de l’intervalle hyperfin de l’atome de ¹³³Cs ou de celui de ⁸⁷Rb.

De telles horloges sont actuellement construites à l’échelle industrielle.

Signalons aussi l’application étudiée par C. Cohen-Tannoudji, S. Haroche et J. Dupont-Roc, qui met en évidence et permet de mesurer des champs magnétiques extrêmement faibles, de l’ordre de 10⁹ à 10¹⁰ G.

Les techniques de pompage optique, qui ont été développées tout d’abord sur les vapeurs monoatomiques diluées, ont été appliquées avec succès par J. Margerie à des ions paramagnétiques et à des centres F dans les cristaux.

Enfin, c’est par un procédé de pompage optique qu’on réalise entre les niveaux d’énergie des ions dans les cristaux l’inversion de population qui permet le fonctionnement des lasers ^{[cf. LASERS]}. À l’équilibre thermique, conformément à la formule de Boltzmann, un niveau quantique supérieur est toujours moins peuplé qu’un niveau inférieur dans l’échelle d’énergie d’un atome ou d’un ion. Grâce à un pompage optique avec un faisceau lumineux intense, on peut peupler davantage un niveau supérieur qu’un niveau inférieur. On dit alors qu’il existe entre les deux niveaux une «inversion de population». Une telle inversion est nécessaire pour que le processus d’émission induite prévu par Einstein l’emporte sur le processus d’absorption et pour déclencher ainsi l’effet laser.

Il existe d’autres procédés que le pompage optique pour obtenir des inversions de population et pour déclencher l’effet laser. Le procédé de pompage optique est utilisé dans le laser à rubis (mis au point par T. H. Maiman en 1960) fondé sur les niveaux d’énergie de l’ion trivalent de chrome dans un cristal de rubis (corindon Al²³, coloré en rose par la présence de ces ions).