CINÉTIQUE
La cinétique, théorie partielle de la mécanique, fait appel aux notions de longueur, de temps et de masse. Elle est le prolongement de la cinématique, puisque son élaboration ne demande que l’introduction d’une nouvelle notion: celle de masse.
On pose comme postulat qu’en chaque point M du domaine de l’espace euclidien où se trouve un ensemble matériel il existe une densité scalaire de masse par unité de volume et l’on définit la masse d’un ensemble mécanique comme étant la somme des masses de ses constituants.
En mécanique classique, on admet par principe que, pour tout ensemble matériel que l’on suit dans son mouvement, la masse est invariante dans le temps. Pour certains ensembles mobiles assez complexes, tels que fusées, câbles de puits d’extraction, etc., il arrive qu’on utilise de manière impropre le terme «systèmes à masses variables»; cela ne signifie nullement que pour de tels ensembles le principe de conservation de la masse soit en défaut, mais cette appellation provient du fait qu’à deux instants on ne met pas en jeu exactement le même système, c’est-à-dire qu’on ne suit pas le système dans son mouvement.
Les entités fondamentales en cinétique sont le centre d’inertie , ou centre de masse, et l’opérateur d’inertie en un point, ainsi que le torseur cinétique , le torseur dynamique , et l’énergie cinétique . La cinétique, indépendamment des renseignements qu’elle fournit sur la répartition de la matière dans un ensemble physique, introduit des grandeurs qui sont systématiquement utilisées dans les applications des principes généraux de la dynamique et de la statique des ensembles matériels quelconques.
Notion de masse
Pour construire la cinétique, il faut, aux notions de longueur et de temps, introduites en cinématique, adjoindre la notion de masse, grandeur fondamentale indépendante des deux précédentes.
Les objets qui nous entourent constituent des ensembles matériels dont nous avons la notion intuitive. On posera comme postulat qu’en chaque point M du domaine de l’espace euclidien occupé par un ensemble matériel existe une densité scalaire de masse 福(M). Si D représente le domaine de l’espace occupé par l’ensemble matériel , la masse est définie de façon abstraite comme une mesure complètement additive définie sur D. La masse de l’ensemble matériel que l’on désigne par m ( ) ou plus simplement par m est par définition:

Cette intégrale est, comme beaucoup de celles qui ont été introduites par la suite, une intégrale au sens de Stieltjes: d 靖 est un élément de volume si D est un volume et l’intégrale est triple; d 靖 est un élément d’aire si D est à deux dimensions (plaque dont on néglige l’épaisseur) et l’intégrale est double; enfin d 靖 est un élément de longueur si D n’a qu’une dimension (tige dont on néglige les dimensions transversales) et l’intégrale est simple. La masse du volume élémentaire (au sens large) qui entoure le point M étant représentée par 福(M)d 靖(M) = dm (M), la masse m s’exprime par la relation:

Si le domaine D est vide de matière, on désigne l’ensemble par 0 et m (0) = 0. Si on fait une partition de quelconque en deux sous-ensembles matériels disjoints, 1 et 2, on a alors m ( ) = m ( 1) + m ( 2).
Dans le système international, l’unité de masse est le kilogramme-masse. Les différentes grandeurs introduites en mécanique classique sont des grandeurs dérivées qui s’expriment en fonction des trois grandeurs fondamentales: longueur, temps, masse.
En mécanique classique, on admet que, quel que soit l’ensemble matériel considéré et quel que soit son mouvement, la masse de ce système est invariante au cours du temps (principe de la conservation de la masse), ce qui conduit à des relations du genre:

auxquelles on a souvent recours en mécanique et que nous utiliserons par la suite sans les rappeler.
Centre d’inertie d’un ensemble matériel
Soit un domaine D de l’espace ordinaire sur lequel est défini en tout point M une mesure 猪(M) et un vecteur み(M); considérer み(M) comme étant la densité d’un champ par rapport à la mesure 猪(M), c’est dire qu’au voisinage de M on associe le vecteur み(M) d 猪(M). À un tel champ vectoriel on associe un torseur 淪( み, 猪), dont les éléments de réduction en un point P sont:

On constate immédiatement que le champ ぬP vérifie la relation des champs de moment de torseur.
Si le champ み(M) est égal à g (M) ゎ ( ゎ est un vecteur indépendant de M, le champ de vecteurs み(M) est un champ de vecteurs parallèles), alors, quelle que soit la mesure 猪, le torseur associé est un torseurvecteur, car le produit scalaire de れ et de ぬP est nul.
De plus, si g (M) = 1 (champ み(M) uniforme), il existe un point H tel que, si 咽M 捻D d 猪(M) n’est pas nulle:

Le point H, ainsi défini indépendant de ゎ, est appelé centre de mesure du domaine D, relatif à la mesure 猪 considérée.
Dans le cas où la mesure 猪(M) est la masse m (M), le centre de mesure de l’ensemble matériel prend le nom de centre d’inertie G, qui se trouve défini par:

ou par la relation équivalente:

Si, par rapport au temps, dans un repère quelconque (), l’on dérive l’égalité vectorielle (1), on obtient immédiatement:

puis, en la dérivant une seconde fois:
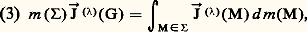
relations dans lesquelles ( size=1凞)(G) et ど( size=1凞)(G) désignent respectivement la vitesse et l’accélération du point G dans son mouvement par rapport au même repère ().
Torseurs cinétique et dynamique
On appelle torseur cinétique (respectivement torseur dynamique ) d’un ensemble matériel , en mouvement par rapport à un repère quelconque (), le torseur associé au champ de vitesse ( size=1凞)(M) (respectivement au champ d’accélération ど( size=1凞)(M)) et à la masse.
Le torseur cinétique notép size=1凞 size=1參 a pour éléments de réduction en un point quelconque H la résultante cinétique et le moment cinétique en H de dans son mouvement par rapport à ().
De même, on définit les éléments de réduction du torseur dynamique: ils sont la résultante dynamique et le moment dynamique en H de dans son mouvement par rapport à () (tabl. 1).
Les relations (2) et (3), en introduisant le centre d’inertie G, permettent d’exprimer les résultantes des torseurs cinétique et dynamique sous la forme:
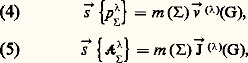
et ces expressions, obtenues à partir de la définition, sont une première mise en évidence de l’importance de la notion de centre d’inertie.
Les égalités (4) et (5) donnent immédiatement la relation entre les résultantes des deux torseurs:

Pour établir la relation entre les moments, on dérive, par rapport au temps, la première relation du tableau 1 dans le repère () et, compte tenu des autres relations, on obtient:

Les relations (6) et (7) sont celles qui existent, dans le cas général, entre résultantes et moments des torseurs cinétique et dynamique en un même point H quelconque.
Lorsque le point H est fixe dans le repère (), ou lorsqu’on prend les éléments de réduction des deux torseurs au centre d’inertie G, la relation (7) se simplifie, le terme m ( )( size=1凞)(H) 廬 ( size=1凞)(G) étant nul.
Si (H) = , ou si H est en G, on a:

Ces deux cas particuliers sont très importants en pratique.
Pour le moment cinétique, on établit la formule:

dans laquelle on désigne par (G) le repère d’origine G, dont les axes sont parallèles à ceux de (). Le mouvement de par rapport au repère (G) est appelé, de manière usuelle, mais impropre, mouvement de autour de son centre d’inertie . La formule correspondante pour le moment dynamique est:

Ces deux relations constituent le théorème de Kœnig qui s’énonce:
Pour un ensemble matériel , en mouvement par rapport à un repère (), le moment cinétique (respectivement dynamique) en un point quelconque H est égal au moment cinétique (respectivement dynamique) en G de , dans son mouvement autour de son centre d’inertie G, augmenté du moment en H de la quantité de mouvement (respectivement quantité d’accélération), par rapport à (), du point G supposé doué de la masse totale m ( ).
Énergie cinétique
On appelle énergie cinétique d’un ensemble matériel , en mouvement par rapport à un repère (), le scalaire E( size=1凞)( ) défini par:

On établit également la formule:

qui constitue le théorème de Kœnig concernant l’énergie cinétique:
L’énergie cinétique d’un ensemble matériel , dans son mouvement par rapport à un repère (), est égale à la somme de l’énergie cinétique de , dans son mouvement autour de son centre d’inertie G, augmentée de l’énergie cinétique dans son mouvement par rapport à () de G qui est supposé doué de la masse totale m ( ).
On remarquera que les définitions, données pour les torseurs cinétique et dynamique et pour l’énergie cinétique, dans le cas d’un ensemble matériel continu, s’étendent immédiatement du cas particulier d’un ensemble matériel formé d’un point matériel unique au cas d’un ensemble discret de points matériels.
Cinétique du solide unique
La notion de solide S a été introduite en cinétique où l’on a établi le résultat fondamental suivant: pour un solide S, le champ de vitesses par rapport à un repère quelconque () est le champ de moments d’un torseur, le torseurS. Autrement dit, quels que soient les deux points M et N marqués sur un même solide S et quel que soit le repère (), on a:

Le centre d’inertie d’un solide S est défini par:

Désignant par (S) un repère lié au solide S, on a, en dérivant cette équation de définition par rapport au temps:

or la vitesse de tout point lié à S étant nulle par rapport à (S), on connaît (S)(G) d’où il résulte que le centre d’inertie G d’un solide S est un point lié au solide.
On introduit alors une quantité qui joue un rôle essentiel en cinétique du solide: par définition, on appelle opérateur d’inertie d’un solide S en un point Q lié à S, l’opérateur linéaire 弄(Q, S) qui, à tout vecteur ゎ, fait correspondre le vecteur 弄(Q,S) ゎ, tel que:

Si l’on désigne par x, y, z les composantes du vecteur QMsur une base liée à S et par u x , u y , u z les composantes du vecteur ゎ sur la même base, la relation précédente s’écrit sous la forme matricielle représentée dans le tableau 2.
Il est à remarquer que l’on aurait une représentation analogue, si la base sur laquelle on projette QMet ゎ n’était pas liée à S; on la choisit toutefois liée à S, parce que, dans ce cas, les intégrales A, B, C, D, E, F sont des constantes par rapport au temps.
A, B, C portent le nom de moments d’inertie par rapport aux axes Qx 轢, Qy 轢, Qzet les quantités D, E, F le nom de produits d’inertie .
L’opérateur 弄(Q, S) étant symétrique, il existe au moins un système de trois vecteurs propres orthogonaux. Le repère d’origine Q et dont les axes sont équipollents à ces trois vecteurs propres est appelé trièdre principal d’inertie en Q pour le solide S. Dans un tel repère orthonormé, la matrice associée à l’opérateur d’inertie est alors diagonale (produits d’inertie nuls).
En tenant compte de la définition du centre d’inertie, on démontre facilement le théorème suivant, dit théorème d’Huygens :
Le moment d’inertie d’un solide S par rapport à une droite est égal au moment d’inertie de S par rapport à la droite G menée par le centre d’inertie G parallèle à , augmenté du produit de la masse m (S) par le carré de la distance d des deux droites:

Le moment cinétique en H d’un solide (S) dans son mouvement par rapport à un repère () s’exprime ainsi:

S est un point lié à (S); cette formule, relativement compliquée, se simplifie dans trois cas particuliers:
H et S confondus en G, alors:

H confondu avec S et S fixe dans (), on obtient:

S choisi en G, ce qui donne:
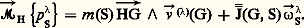
Dans le cas d’un solide, la formule de définition de l’énergie cinétique conduit à l’expression développée:

qui se simplifie dans deux cas particuliers importants; celui pour lequel S est choisi en G, ce qui conduit à:

et celui pour lequel S est fixe dans (), à partir de quoi l’on obtient alors:

On peut désigner par p, q, r les composantes du vecteur ゚ size=1凞S sur les axes liés au solide S; si les composantes de l’opérateur d’inertie en S, dans la même base ( ゑS, をS, んS), sont celles du tableau 2, les quantités cinétiques:
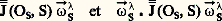
ont pour expressions effectives:

Si S ゑS をS んS est le trièdre principal d’inertie de S en S, ces expressions se simplifient puisque D, E, F sont nuls.
cinétique [ sinetik ] n. f. et adj.
• 1877; gr. kinêtikos « qui se meut; qui met en mouvement »
I ♦ N. f.
1 ♦ Phys. Branche de la mécanique qui étudie la relation entre les forces appliquées et la cinématique des corps et des systèmes.
2 ♦ Chim. Étude de la vitesse des réactions chimiques ou enzymatiques.
II ♦ Adj.
1 ♦ Phys. Qui a le mouvement pour principe. Énergie cinétique : moitié de la force vive d'un point mobile de masse m et de vitesse v (1/2 mv2). Énergie cinétique relativiste, en fonction de c, vitesse de la lumière. — Théorie cinétique des gaz.
2 ♦ (1920) Art cinétique : forme d'art plastique fondé sur le caractère changeant d'une œuvre par effet optique (mouvement réel ou virtuel).
● cinétique adjectif (grec kinêtikos) Relatif au mouvement. ● cinétique (expressions) adjectif (grec kinêtikos) Art cinétique, forme d'art contemporain issue de l'abstraction et fondée sur le caractère changeant de l'œuvre, son mouvement apparent ou réel. Énergie cinétique, pour un point mobile de masse m et de vitesse v, grandeur
 .
Moment cinétique, pour un point mobile de masse m et de vecteur vitesse
.
Moment cinétique, pour un point mobile de masse m et de vecteur vitesse  , moment, en un point donné, de la quantité de mouvement
, moment, en un point donné, de la quantité de mouvement  du point.
Théorie cinétique des gaz, théorie statistique qui rend compte des propriétés macroscopiques d'un fluide à partir des mouvements des particules le constituant.
● cinétique (synonymes)
adjectif
(grec kinêtikos)
Moment cinétique
du point.
Théorie cinétique des gaz, théorie statistique qui rend compte des propriétés macroscopiques d'un fluide à partir des mouvements des particules le constituant.
● cinétique (synonymes)
adjectif
(grec kinêtikos)
Moment cinétique
Synonymes :
● cinétique
nom féminin
Théorie expliquant un ensemble de phénomènes à partir des seuls mouvements des particules matérielles.
Étude des lois qui régissent la vitesse des réactions chimiques.
cinétique
adj. et n. f.
rI./r adj.
d1./d Relatif au mouvement.
d2./d PHYS énergie cinétique: énergie emmagasinée par un corps lors de sa mise en mouvement, égale à 1/2 mV2 si le corps est en translation ou à 1/2 Jomega2 s'il est en rotation (m: masse; V: vitesse; J: moment d'inertie par rapport à l'axe de rotation; omega: vitesse angulaire).
— Moment cinétique par rapport à un point: moment, par rapport à ce point, de la quantité de mouvement.
— Théorie cinétique des gaz, qui déduit les propriétés des gaz de l'étude du mouvement d'agitation de leurs molécules.
d3./d BX-A Art cinétique: courant de l'art plastique contemp. qui fait appel aux effets de mouvement réel ou virtuel.
rII./r n. f.
d1./d PHYS étude descriptive du mouvement d'un système de particules caractérisées par leur masse.
d2./d CHIM Cinétique chimique: étude de la modification de la composition d'un système chimique en fonction du temps.
⇒CINÉTIQUE, adj. et subst. fém.
I.— Adjectif
A.— Qui se rapporte ou qui est dû au mouvement. La nature cinétique ou vibratoire des rayons (M. DE BROGLIE, Les Rayons X, 1922, p. 23) :
• Le mésencéphale et le cortex se répartissent les deux grands aspects de la motricité, l'activité tonique ou posturale et l'activité cinétique ou de relation.
MOUNIER, Traité du caractère, 1946, p. 192.
B.— Spécialement
1. MÉCAN. Énergie cinétique. Énergie liée au mouvement d'un corps, qui s'annule quand le corps s'immobilise (cf. F. PERRIN, La Dynamique relativiste et l'inertie de l'énergie, 1932, p. 10). Moment cinétique. Moment du vecteur « quantité de mouvement » (cf. R. DAUDEL, Les Fondements de la chim. théorique, 1956, p. 25).
2. PHYS. Théorie cinétique de la matière, des fluides (gaz, liquides, plasmas). Théorie qui détermine les propriétés des corps par l'analyse des mouvements de leurs molécules. La théorie cinétique des gaz avait permis à Loschmidt de déterminer une valeur approximative du nombre de molécules contenues dans une molécule-gramme (ou mole), ou nombre d'Avogadro (Hist. gén. des sc., t. 3, vol. 2, 1964, p. 229).
3. Art cinétique. Forme d'art plastique comprenant des œuvres en mouvement (machines, mobiles), ou combinant la lumière et le mouvement (œuvres lumino-cinétiques), ou donnant l'illusion du mouvement (œuvres en mouvement virtuel) (cf. Encyclop. univ., 1972, p. 534, 535).
II.— Subst. fém.
A.— PHYS. Étude du mouvement des corps, faisant appel aux notions de longueur, de temps et de masse.
B.— CHIM. Cinétique chimique. Étude du mécanisme et de la vitesse des réactions chimiques (cf. M. CURIE, Luminescence des corps solides, 1934, p. 6). Synon. cinétique des réactions.
Prononc. et Orth. :[sinetik]. Ds Ac. 1932. Adj. kinétique ds RICŒUR, Philos. de la volonté, 1949, p. 225. Étymol. et Hist. 1877 adj. et subst. (LITTRÉ Suppl.). Empr. au gr. « qui met en mouvement ». Fréq. abs. littér. :36.
« qui met en mouvement ». Fréq. abs. littér. :36.
 « qui met en mouvement ». Fréq. abs. littér. :36.
« qui met en mouvement ». Fréq. abs. littér. :36.
cinétique [sinetik] adj. et n. f.
ÉTYM. 1877; grec kinêtikos « qui met en mouvement; qui se meut », de kinêtos « mobile », de kinein « mouvoir » (→ -cinésie).
❖
♦ Didactique.
1 Adj. Qui a le mouvement pour principe. || Théorie cinétique des gaz, de la matière. || Énergie cinétique : moitié de la force vive d'un point matériel en mouvement (1/2 m v2).
♦ (1920). || Art cinétique : forme d'art plastique fondée sur le caractère changeant d'une œuvre par effet optique (mouvement réel ou virtuel).
2 N. f. || Cinétique chimique : étude de la vitesse et du mécanisme des réactions chimiques.
♦ Théorie expliquant un ensemble de phénomènes par le mouvement de la matière.
3 Sémiol. ⇒ Kinésique.
❖
COMP. Autocinétique, électrocinétique, hétérocinétique, homocinétique, monocinétique, pharmacocinétique.
Encyclopédie Universelle. 2012.