Akademik

PLASMAS

PLASMAS

Le terme «plasma» a été introduit en physique en 1923 par les physiciens américains Irving Langmuir et Levi Tonks pour désigner, dans les tubes à décharge (cf. état GAZEUX), certaines régions équipotentielles contenant un gaz ionisé électriquement neutre. Par la suite, ce mot a été utilisé, surtout en astrophysique, pour désigner un état dilué de la matière, analogue à un gaz, mais constitué de particules chargées, électrons et ions positifs, en proportions telles que le milieu soit globalement neutre. Le plus simple des plasmas est celui d’hydrogène, formé d’électrons et de protons libres en concentrations égales. Ainsi définis, les plasmas se confondent donc avec les gaz complètement ionisés. Ils constituent un quatrième état de la matière, faisant suite, dans l’échelle des températures, aux trois états classiques, solide, liquide et gaz. Les propriétés spéciales des plasmas sont dues au long rayon d’action de la force entre particules (force coulombienne): un électron ou un ion du plasma interagit ainsi à chaque instant avec beaucoup d’autres. On peut même décrire de nombreuses propriétés des plasmas (effets collectifs) en considérant ceux-ci comme des mélanges de deux fluides continus d’électricité positive et négative. Par suite de leur faible densité, les plasmas conservent cependant certaines propriétés des gaz (grande compressibilité, énergie interne et pression proportionnelles à la température absolue, etc.).

La transition entre les gaz neutres et les plasmas complètement ionisés est assurée par les gaz partiellement ionisés. Par abus de langage, on donne également souvent à ceux-ci le nom de plasmas dans la mesure où ils sont électriquement neutres. En fait, les propriétés mécaniques (écoulements, ondes acoustiques, etc.) des gaz faiblement ionisés sont analogues à celles des gaz neutres, tandis que leurs propriétés électromagnétiques (conductivité électrique, indice de réfraction, par exemple) en diffèrent par suite de la présence d’électrons libres en leur sein.

Bien que l’analyse théorique des plasmas soit relativement simple (forces entre particules connues exactement, description par la mécanique classique possible en général), leur étude ne s’est développée que depuis 1950. Des techniques sont apparues (hyperfréquences, puis lasers) qui permettent de mesurer avec précision les paramètres fondamentaux des plasmas: densité et température électroniques, fréquence de collision des électrons. Grâce au développement de la radioastronomie puis de la recherche spatiale, on a pu explorer les plasmas de l’environnement terrestre: ionosphère, magnétosphère, vent et couronne solaires. De façon plus générale, la physique des plasmas joue un rôle très important dans toute l’astrophysique et la cosmologie: on pense que plus de 99 p. 100 de l’Univers est constitué par de la matière à l’état de plasma. Des problèmes de plasmas sont apparus dans de nombreuses techniques nouvelles où l’on produit de hautes températures: explosions nucléaires, conversions magnétohydrodynamique et thermoïonique de l’énergie, rentrée des objets spatiaux dans l’atmosphère, propulsion électrique des satellites, lasers à gaz, découpage des métaux par chalumeau à plasma, par exemple.

Enfin, une application des plasmas, qui paraît encore futuriste mais qui peut être capitale pour l’avenir de l’humanité, a fait l’objet, surtout depuis 1955, de vastes programmes de recherches: il s’agit de la domestication des réactions nucléaires que l’on produit dans les bombes H, à savoir les réactions de fusion des noyaux légers (deutérium, tritium) en noyaux d’hélium. Le fonctionnement d’un tel réacteur à fusion nécessite la production et le confinement pendant un temps suffisant d’un plasma de deutérium et de tritium de densité assez élevée et de température dans la gamme dite thermonucléaire (face=F0019 礪黎 10⁷ K). La plupart des méthodes proposées utilisent des champs magnétiques pour effectuer le confinement, et le but visé se révèle très difficile à atteindre, du fait des nombreuses oscillations et instabilités qui tendent à se produire dans les plasmas se trouvant placés dans un champ magnétique.

1. Gaz ionisés et plasmas

Degré d’ionisation

Dans leur état normal, les gaz sont des isolants électriques. Cela tient au fait qu’ils ne contiennent pas de particules chargées libres, mais seulement des molécules neutres. Cependant, si on leur applique des champs électriques assez intenses, ils deviennent conducteurs; les phénomènes complexes qui se produisent alors portent le nom de décharges dans les gaz et sont dus à l’apparition d’électrons et d’ions libres.

Le résultat d’une décharge dans un gaz est donc la production d’un gaz ionisé contenant par exemple n^e électrons, nⁱ ions positifs, et n^o molécules neutres par centimètre cube. La haute atmosphère terrestre, les atmosphères stellaires et les nébuleuses sont également constituées de gaz ionisés; en général, le gaz est macroscopiquement neutre. On a alors:

Cette neutralité est la conséquence des forces électrostatiques très intenses qui apparaissent dès que l’on a n^e nⁱ .

Le degré d’ionisation d’un gaz est défini par le rapport:

où n^o est la densité (nombre de particules par unité de volume) des molécules neutres et n celle des molécules ionisées.

La valeur du degré d’ionisation dans les divers types de gaz ionisés varie en pratique depuis des valeurs très faibles, de l’ordre de 10 size=1^漣¹⁰, par exemple, jusqu’à 1; nous classerons d’une façon provisoire, qui sera justifiée ultérieurement, les gaz ionisés en deux familles:

– gaz faiblement ionisés: 見麗 10 size=1^漣⁴,

– gaz fortement ionisés: 見礪 10 size=1^漣⁴.

Quand le degré d’ionisation est égal à l’unité, la densité des molécules neutres est nulle; on dit que le gaz est totalement ionisé, ou encore qu’il constitue un plasma . L’origine de ce nom tient au fait que le milieu peut alors être le support d’oscillations de charge d’espace qu’on décrira plus loin et qu’on appelle «oscillations de plasma», car elles ressemblent à des vibrations d’un milieu gélatineux. En fait, on désigne maintenant souvent sous le nom de plasma n’importe quel gaz ionisé.

Ionisation thermique d’un gaz

Lorsqu’on chauffe un gaz à une température T suffisamment élevée (de l’ordre de 10⁴ K), l’énergie moyenne (3/2) k T de translation de ses molécules (cf. état GAZEUX) peut devenir du même ordre que leur énergie d’ionisation Eⁱ ; dans ces conditions, lorsque deux molécules entrent en collision, il peut y avoir ionisation de l’une d’entre elles.

Si le gaz est en équilibre thermodynamique , l’ionisation par collisions est contrebalancée par des processus de recombinaison entre électrons et ions et il en résulte que les trois variables 見, n et T ne sont pas indépendantes. L’ionisation est déterminée par la densité et la température; on dit alors que le gaz est en état d’équilibre d’ionisation thermique. Les propriétés de cet équilibre sont décrites dans le cas simple d’un gaz monoatomique par une formule établie en 1920 par l’astrophysicien M. N. Saha:

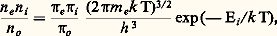
où m^e est la masse de l’électron, k la constante de Boltzmann, h la constante de Planck, 神^e , 神ⁱ et 神^o , les poids statistiques respectifs de l’électron, de l’ion et de l’atome neutre; on a, en outre, 神^e = 2.

À des températures plus élevées, les atomes du gaz peuvent d’ailleurs s’ioniser plusieurs fois. À titre d’exemple, la figure 1 montre en fonction de T les concentrations X^A, X^A+ X^A2+, ... des diverses espèces d’ions dans l’argon en équilibre à la pression atmosphérique. On voit que le gaz est ionisé à 90 p. 100 vers 16 000 K et doublement ionisé vers 28 000 K.

Plasmas hors d’équilibre thermique

Dans de nombreux cas, l’ionisation est produite par un champ électrique extérieur, et le gaz n’est pas en équilibre thermodynamique. Il atteindra souvent un état stationnaire qu’on pourra caractériser par les paramètres 見, n , T^e (température des électrons), Tⁱ (température des ions) et T^o (température des molécules).

Les trois températures ainsi introduites sont définies par la condition que (3/2)k T^a représente l’énergie cinétique moyenne des particules d’espèce a .

L’écart entre T^e , Tⁱ et T^o peut être important: par exemple, dans un tube à décharge typique, on pourra avoir: T^o 力 Tⁱ 力 300 K et T^e 力 3 憐10⁴ K. La forte valeur de T^e est due à l’action du champ électrique sur les électrons, et l’ionisation est alors produite par les collisions de ces électrons chauds sur les molécules neutres du gaz.

Densité et température des plasmas usuels

Les valeurs de n et de T que l’on a à considérer dans les divers plasmas variant énormément, il est commode de représenter les plasmas sur un diagramme dont les coordonnées sont:

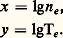
Si le gaz est en équilibre thermodynamique, T^e = T, et le diagramme permet de définir, comme on vient de le dire, tous les états du gaz; si celui-ci est simplement dans un régime stationnaire hors d’équilibre, il ne le permettra que si on suppose fixés les paramètres 見, Tⁱ et T^o . À titre d’exemple, le tableau 1 fournit des valeurs typiques de x et y pour les plasmas rencontrés dans divers domaines de la physique.

Pour exprimer les températures dans les plasmas chauds, on utilise souvent l’électron-volt (valeur de k T dans cette unité) au lieu du degré K. La règle de conversion est:

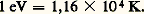
Familles de gaz ionisés

Dans l’ensemble des gaz ionisés, on peut donc distinguer trois familles:

a ) Les gaz faiblement ionisés ( 見麗 10 size=1^漣⁴) dans lesquels quelques ions et électrons se déplacent au milieu d’une mer de molécules neutres; ce sont alors les collisions binaires entre un électron (ou un ion) et une molécule qui déterminent la dynamique des particules chargées.

b ) Les gaz fortement ionisés sans interactions entre particules; ce sont des plasmas suffisamment dilués (par exemple, le vent solaire) dans lesquels les particules chargées suivent sans aucune collision une trajectoire essentiellement déterminée par les champs électromagnétiques d’origine extérieure.

c ) Les gaz fortement ionisés avec interactions entre particules. On démontre alors que, souvent, un électron particulier peut être considéré comme en interaction avec un grand nombre d’autres particules chargées. Ce sont ces interactions coulombiennes dites collectives qui déterminent essentiellement la dynamique du plasma.

Écarts à la neutralité: longueurs de Debye, oscillations de plasma

Si, dans un plasma initialement neutre, on produit une perturbation locale sous la forme d’un excès de charge électrique positive ou négative, celui-ci va tendre à revenir vers l’état d’équilibre de neutralité. Cependant, on peut voir facilement que la perturbation initiale engendre en général une oscillation pendulaire non amortie du plasma autour de son état d’équilibre. Considérons, par exemple, la situation représentée sur la figure 2: à l’instant initial, la région grisée contient un excès d’électrons qui produit un champ électrique tendant à créer un mouvement des électrons dans le sens des flèches. Dans ce mouvement, ceux-ci acquerront une certaine énergie cinétique, et ils pourront, au bout d’un certain temps, dépasser la position d’équilibre. Un trop grand nombre d’électrons ayant quitté la région grisée, il y aura un défaut d’électrons dans cette région, et un champ électrique tendant à les ramener vers elle. Au bout d’un certain temps, la situation initiale est reconstituée et le cycle recommence. Les vibrations ainsi produites sont appelées oscillations de plasma électroniques.

Dans ces oscillations, les ions beaucoup plus lourds que les électrons restent pratiquement immobiles. L’agitation thermique et les collisions jouent en général un rôle négligeable, et un calcul simple permet alors d’obtenir la pulsation 諸^p des oscillations de plasma par la formule:

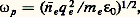
où q^e est la charge de l’électron et 讀^e la densité électronique du plasma non perturbé.

On peut également perturber la neutralité d’un plasma en y introduisant une électrode métallique. On constate alors que le plasma, s’il est assez dense, fait écran à la perturbation électrique apportée par l’électrode: la masse du plasma reste électriquement neutre et équipotentielle; le champ électrique et les écarts à la neutralité sont limités à une gaine entourant l’électrode; l’épaisseur de cette gaine est donnée en ordre de grandeur par la longueur de Debye :

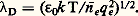
Les mêmes effets d’écran se manifestent au niveau microscopique; la neutralité électrique, qui s’exprime par la condition:

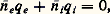
où q^e est la charge de l’électron et qⁱ la charge des ions du plasma, n’est qu’une propriété des valeurs moyennes 讀^e et 讀ⁱ des densités électronique et ionique. Une analyse plus fine fait apparaître des corrélations de position entre les électrons et les ions: autour de chaque ion, il y a un certain excès d’électrons. Il en résulte que le potentiel électrostatique autour de chaque ion du plasma est donné par la formule:

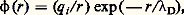
où le facteur qⁱ /r est le potentiel de Coulomb de l’ion tout seul; l’exponentielle représente l’effet d’écran dû aux électrons corrélés à cet ion.

2. Gaz faiblement ionisés

Théorie cinétique des gaz faiblement ionisés

Lorsque le degré d’ionisation d’un gaz ionisé est assez bas, les électrons et les ions interagissent seulement avec les molécules neutres. On dira qu’on est en présence d’un gaz faiblement ionisé; le critère qui définit cette famille est donc:

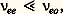
où 益^ee et 益^eo sont les fréquences de collisions électron-électron et électron-neutre. L’image qu’on peut se faire d’un tel gaz est celle d’une «mer» de molécules neutres dans laquelle se déplacent quelques électrons et ions; chacun de ceux-ci évolue indépendamment de ses pairs en effectuant des collisions binaires aléatoires sur les neutres (fig. 3).

La dynamique de la «mer» de molécules n’est pas influencée par le mouvement des particules chargées: les conditions aux limites permettent de déterminer son état et plus précisément la fonction de distribution f^o (w^o ) des vitesses w^o des molécules. Dans le cas simple où le gaz est en équilibre avec un thermostat, f^o est une fonction maxwellienne avec une température T^o égale à celle du thermostat (cf. théorie CINÉTIQUE DES FLUIDES).

La dynamique des particules chargées s’étudie au moyen de deux équations de Boltzmann indépendantes déterminant les fonctions de distribution f^e (w^e ) des électrons et fⁱ (wⁱ ) des ions; f^o (w^o ) y joue le rôle d’un paramètre. L’étude du mouvement des électrons est plus facile car on peut y considérer que les molécules sont des centres de forces fixes de masse infinie: elles agissent comme des diffuseurs aléatoires qui s’opposent à tout mouvement ordonné des électrons; d’autre part, l’échange d’énergie entre les électrons et les molécules lors des collisions élastiques est très faible par suite de la très petite valeur du rapport m^e/m^o des masses des deux espèces de particules. La théorie cinétique que l’on bâtit sur ces idées est connue sous le nom de modèle de Lorentz . Elle conduit à définir deux temps de relaxation entre électrons et molécules, soit respectivement le temps de relaxation des anisotropies et le temps de relaxation de l’énergie:

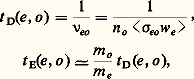
où 靖^eo est la section efficace de transfert de quantité de mouvement par collision électron-molécule. La comparaison de ces deux temps de relaxation avec le temps t^ee de collision électron-électron permet de distinguer deux familles dans l’ensemble des gaz faiblement ionisés, celle des gaz très faiblement ionisés, qui correspond aux relations:

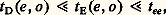
et celle des plasmas intermédiaires, définie par:

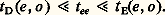
Dans la première, les collisions e-e ne jouent aucun rôle; dans la deuxième, elles sont suffisantes pour que les électrons constituent un sous-système thermodynamique avec une distribution maxwellienne et une température T^e , le bilan des échanges d’énergie (faibles) avec les molécules neutres déterminant la valeur de T^e . La figure 4 montre, dans le cas de l’hélium, le domaine d’existence de ces familles de plasmas.

Si l’on crée un champ électrique E dans un gaz faiblement ionisé, il en résulte un courant électrique; les collisions e-o limitent la valeur de ce courant et transforment l’énergie fournie par le champ E en énergie désordonnée des électrons; il y a donc échauffement des électrons: c’est l’effet Joule. Après un intervalle de temps de l’ordre de t ^E(e , o ), les électrons du gaz tendent vers un état stationnaire où l’échauffement par effet Joule est compensé par un refroidissement dû aux collisions sur les neutres. On montre que, dans cet équilibre, T^e est fonction de T^o et du rapport E/n^o . La figure 5 montre, dans le cas d’un plasma intermédiaire d’hélium, la variation de T^e en fonction de E/n^o pour deux valeurs de T^o ; on y voit que, si E/n^o est assez fort, l’équilibre du gaz s’établit à des valeurs de T^e 拾 T^o .

Équations macroscopiques et coefficients de transport

Partant des équations de Boltzmann relatives aux électrons et aux ions, on obtient, par la méthode «régressive» (cf. théorie CINÉTIQUE DES FLUIDES), les équations macroscopiques correspondantes pour les électrons:

a ) équation de la conservation des électrons:

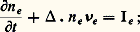
b ) équation de transport de la quantité de mouvement:

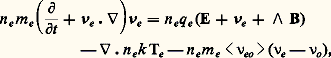
ainsi que deux équations analogues pour les ions; I^e est le terme de production d’électrons (bilan des réactions d’ionisation et de recombinaison) et 麗益^eo 礪 introduit un effet de frottement des électrons sur les neutres. Ces équations macroscopiques sont l’outil essentiel pour l’étude de nombreuses propriétés de gaz faiblement ionisés. Appliquées à certaines situations très simples, elles permettent de définir des coefficients de transport faciles à mesurer et de faire la liaison avec la théorie cinétique; les deux principaux sont la mobilité électrique 猪 et le coefficient de diffusion D définis, dans le cas des électrons, par les formules:

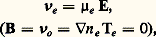
et:

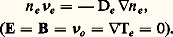
La théorie cinétique permet de calculer 猪^e et D^e , et donne:

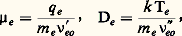
où 益 ^eo et 益 ^eo sont des moyennes pondérées convenablement de la fréquence de collision 益^eo . En général, 猪^e et D^e sont inversement proportionnelles à n^o et fonctions de la température T^e ou, ce qui revient au même, du rapport E/n^o .

La figure 6 montre, par exemple dans le cas des gaz rares, la loi de variation de la mobilité réduite 猪^eo en fonction de E/n^o (la mobilité réduite est le produit 猪^en^o/n ^L, où n ^L est la densité particulaire normale d’un gaz parfait).

Les coefficients de transport 猪ⁱ et Dⁱ des ions s’expriment par des formules analogues à celles donnant 猪^e et D^e ; cependant, du fait de leur plus grande masse, les ions sont beaucoup moins mobiles et l’on a:

Le tableau 2 donne les valeurs expérimentales des mobilités réduites électroniques et ioniques correspondant aux faibles valeurs de E/n^o pour quelques gaz.

La grande disparité entre les coefficients de diffusion D^e et Dⁱ ne peut s’observer que si le plasma considéré est très peu dense et de faibles dimensions; les deux espèces de particules peuvent alors diffuser indépendamment et librement. En fait, il y a en général un couplage électrostatique entre les diffusions des deux espèces de particules; le plasma tendant à rester neutre, les électrons et les ions diffusent solidairement: c’est ce qu’on appelle la diffusion ambipolaire . La condition d’observation de ce phénomène est que la longueur de Debye du plasma soit bien plus petite que les dimensions du récipient contenant le plasma. On a alors:

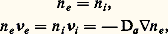
où D^a , coefficient de diffusion ambipolaire, est une combinaison des quatre coefficients de transport élémentaires:

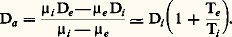
Ce coefficient de diffusion ambipolaire est donc, en général, de l’ordre de grandeur du coefficient de diffusion libre des ions.

3. Plasmas sans interactions

Notion de gaz d’électrons et d’ions libres

Lorsque la densité d’un plasma est assez basse, on peut souvent négliger les interactions entre particules; les mouvements des électrons et des ions sont alors déterminés uniquement par les champs électromagnétiques régnant dans le plasma. On obtient ainsi ce qu’on peut appeler un gaz d’électrons et d’ions libres; bien entendu, ce modèle est un cas limite; tous les gaz réels contiennent les trois types de particules déjà mentionnées, de sorte que les électrons subiront toujours des collisions avec une certaine fréquence 益¹. Cependant, considérons un électron soumis soit à un champ magnétique uniforme B, soit à un champ électrique alternatif de pulsation 諸; dans les deux cas, son mouvement contient une composante périodique. Supposons que l’on ait l’une des deux inégalités:

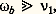
諸^b étant la vitesse angulaire gyromagnétique de l’électron, ou bien:

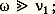
le mouvement de l’électron aura ainsi l’allure représentée sur les figures 7 ou 8. On conçoit alors que les propriétés du gaz seront peu affectées par les collisions; on pourra étudier comme une première approximation un modèle obtenu en négligeant totalement les collisions.

Dérive et conductivité électrique dans un champ magnétique uniforme

Dans les conditions que l’on vient d’évoquer, l’étude des propriétés d’un plasma se ramène à celle des trajectoires des particules chargées dans un champ électromagnétique d’origine extérieure. Les cas les plus simples sont les suivants:

Champ magnétique B uniforme; champ électrique E nul

Les trajectoires des électrons et des ions sont des hélices régulières enroulées autour du champ magnétique et décrites pour chaque espèce de particules avec la vitesse angulaire:

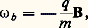
où q et m sont la charge électrique et la masse de la particule.

Les rayons et les pas des hélices ont une distribution statistique déterminée par les fonctions de distribution des vitesses électroniques et ioniques. En général, ces mouvements désordonnés ne donnent lieu à aucun mouvement d’ensemble dans le repère considéré.

Champ magnétique B uniforme; champ électrique E uniforme et indépendant du temps

Si le champ magnétique B est uniforme, le champ électrique E étant aussi uniforme et indépendant du temps, le comportement se déduit de celui que l’on vient d’étudier par un simple changement de repère relativiste (cf. ÉLECTRICITÉ - Électromagnétisme). On peut alors montrer que l’ensemble du plasma, électrons et ions, se déplace dans la direction perpendiculaire à la fois à E et B avec la vitesse:

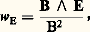
appelée vitesse de dérive électrique. Les trajectoires des particules, projetées sur le plan perpendiculaire à B, sont des courbes cycloïdales. La figure 9 représente, à titre d’exemple, deux trajectoires relatives l’une à un électron, l’autre à un ion, ayant initialement une vitesse nulle. On n’a pas représenté les mouvements parallèles à B qui, sous l’influence de E size=1^瑩, sont accélérés en sens inverse, mais seulement le mouvement de dérive. L’ion part tout d’abord dans la direction électrique E size=1^旅, puis, sous l’effet du champ magnétique, sa trajectoire se courbe, et décrit une série d’arceaux. L’électron part tout d’abord en sens inverse, mais la courbure de sa trajectoire est également en sens inverse. C’est pourquoi son mouvement de dérive s’effectue dans le même sens que celui de l’ion. Du fait que la masse de l’électron est beaucoup plus petite que la masse d’un ion, les arceaux qu’exécute l’électron sont bien plus petits, mais il en effectue un plus grand nombre par seconde, de telle sorte que les deux vitesses de dérive sont finalement égales.

Champ magnétique B uniforme, champ électrique E uniforme alternatif de pulsation size=4諸

Dans un champ magnétique B uniforme et dans un champ électrique E uniforme alternatif de pulsation 諸, électrons et ions sont animés, en plus de leurs mouvements hélicoïdaux désordonnés, d’oscillations d’ensemble ayant une fréquence angulaire 諸; il en résulte une densité de courant électrique j à cette même fréquence dont l’amplitude complexe est liée à celle de E par la formule:

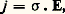
靖 est la conductivité électrique . La présence de B donne au plasma un caractère anisotrope de sorte que j et E ne sont pas colinéaires et 靖 est donc un tenseur. La conductivité est la somme de deux composantes, l’une électronique, l’autre ionique. Si on prend comme axe Oz la direction du champ magnétique, le tenseur de conductivité électronique s’écrit:

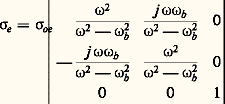
avec:

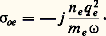
En l’absence de champ magnétique, ce tenseur se réduit à ses composantes diagonales, on a:

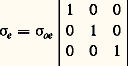
En présence d’un faible champ magnétique ( 諸^b 廉諸), le plasma devient anisotrope: seule la conductivité dans la direction de B est inchangée; les deux premiers termes diagonaux diffèrent du troisième par un terme du deuxième ordre en 諸^b / 諸; cette variation de la conductivité dans les directions perpendiculaires à B porte le nom de magnétorésistance ; enfin, il apparaît des termes non diagonaux qui donnent une composante de courant perpendiculaire à la fois à E et à B; ces termes constituent ce que l’on appelle l’effet Hall ; c’est un effet du premier ordre en 諸^b / 諸.

Si le champ magnétique est assez fort, ou si la fréquence est assez basse pour que l’on ait 諸廉諸^b , la conductivité dans la direction de l’axe Oz est encore inchangée. Par contre, tous les autres termes tendent vers zéro, les termes diagonaux comme 靖^oe ( 諸²/ 諸^2b ) et les termes d’effet Hall comme 靖^oe ( 諸/ 諸^b ) en valeur absolue.

Les propriétés de conductivité électrique que l’on vient d’analyser permettent d’étudier la propagation des ondes de hautes fréquences dans les plasmas; l’application la plus importante de cette théorie concerne la propagation des ondes radio dans l’ionosphère.

Pour les ondes de basses fréquences, l’expression du tenseur de conductivité donnée ci-dessus doit d’ailleurs être modifiée: d’une part, il faut tenir compte des collisions , ce qu’on peut faire en première approximation en remplaçant, dans l’expression de 靖, j 諸 par j 諸 + 益¹; d’autre part, 靖 devient alors fonction non seulement de 諸 (dispersion temporelle ) mais aussi du vecteur d’onde k de l’onde considérée (dispersion spatiale ); ce dernier effet est important dans les ondes lentes de vitesse de phase 益﨏 = 諸/k plus petite que la vitesse moyenne d’agitation thermique des électrons.

Trajectoires adiabatiques dans un champ B non uniforme

Condition d’adiabaticité

Quand le plasma se trouve dans un champ magnétique non uniforme, le calcul des trajectoires des électrons et des ions ne peut plus se faire en général de façon simple. Il y a cependant un cas très important où l’on peut étudier de façon approchée les propriétés générales du mouvement des particules, c’est celui des champs presque uniformes et presque statiques. Plus précisément, on supposera satisfaites les deux hypothèses suivantes:

a ) La variation de B dans l’espace est suffisamment lente, et B suffisamment fort, pour que sa variation relative, sur une distance égale à un rayon de gyration r^b des particules, soit faible.

b ) La variation de B dans le temps est suffisamment lente, et B suffisamment fort, pour que sa variation relative, sur un intervalle de temps égal à une période gyromagnétique 1/ 益^b des particules, soit faible.

Quand les deux hypothèses ci-dessus sont satisfaites, on peut, par une méthode d’approximation dite adiabatique, considérer qu’à un instant donné la trajectoire de chaque particule est une hélice; cependant, à cause des variations du champ magnétique, cette hélice se déforme progressivement.

Mouvement quasi hélicoïdal et dérives

On peut étudier tout d’abord le cas le plus simple où B est constant dans le temps, et le champ électrique nul.

La figure 10 représente alors le mouvement le plus général d’une particule M; ce mouvement peut se décomposer en écrivant:

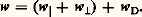
Les deux premiers termes du deuxième membre représentent un mouvement quasi hélicoïdal autour des lignes de force de B; la particule M tourne autour d’un centre instantané C dans un plan perpendiculaire à B avec la vitesse w size=1^旅; le centre instantané C se déplace le long d’une ligne de force, avec la vitesse w size=1^瑩.

Le terme w^D représente un mouvement lent de C perpendiculairement aux lignes de force; on l’appelle une vitesse de dérive .

Le mouvement quasi hélicoïdal ne se fait pas sur une hélice droite régulière, parce que les lignes de force sont en général courbées et convergentes ou divergentes.

On montre que, si les dérives étaient négligeables, l’orbite serait tracée sur un tube de force avec conservation approximative de la quantité:

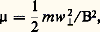
qui représente le moment magnétique associé au mouvement circulaire de la particule.

Lorsque la particule pénètre dans une région de champ magnétique croissant, l’invariance de 猪 montre que w size=1^旅 croît au détriment de w size=1^瑩; la particule a son mouvement longitudinal freiné par l’augmentation de B; l’énergie longitudinale est transformée en énergie transversale.

Si la variation de B est assez importante, le transfert d’énergie peut être complet: il existe une abscisse où w size=1^瑩 s’annule; la particule est réfléchie à cet endroit et repart vers les rayons de plus faible champ magnétique; c’est pourquoi on dit qu’une région où B est croissant constitue un miroir magnétique .

On appelle rapport de miroir la quantité:

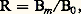
où B⁰ est le champ magnétique dans une section initiale S⁰ où passent toutes les particules et B^m le champ magnétique maximal au niveau du «col» S^m (fig. 11). Soit w⁰ la vitesse initiale d’une certaine particule dans la section S⁰ et ⁰ l’angle de cette vitesse avec B⁰.

On peut définir une valeur critique ^0m de ⁰ telle que:

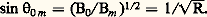
Les particules dont la vitesse initiale w ⁰ est comprise à l’intérieur du cône, appelé cône de perte , pour lequel 麗 ^0m traversent le miroir.

Au contraire, les particules dont la vitesse initiale est en dehors du cône de perte se réfléchissent toutes avant le col, dans une section d’autant plus rapprochée de S⁰ que la vitesse initiale w⁰ est plus écartée de la ligne de force centrale.

En plus des effets de freinage et de miroir magnétique, la non uniformité de B produit une légère vitesse de dérive w^D qui se superpose au mouvement quasi hélicoïdal. On démontre que cette vitesse de dérive se décompose en deux termes:

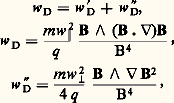
w ^D peut être appelée la dérive de courbure des lignes de force. On peut en effet l’écrire:

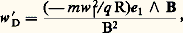
e ¹ étant le vecteur unitaire porté par la normale principale à la ligne de force centrale, et R le rayon de courbure de cette ligne de force (fig. 10); cette écriture permet

de considérer w ^D comme due à la force centrifuge agissant sur C dans son mouvement longitudinal et produisant un effet analogue à celui que nous avons décrit pour un champ électrique.

La composante w ^D peut être appelée la dérive de gradient . C’est un effet proportionnel à w ² size=1^旅 et indépendant de w size=1^瑩. On peut la justifier qualitativement en considérant les particules se déplaçant dans un plan perpendiculaire à B, pour lequel w size=1^瑩 = 0; en présence d’un gradient, le rayon de courbure de la trajectoire varie périodiquement; il est plus petit quand la particule est du côté où B croît et plus grand quand elle est de l’autre côté. Il en résulte une trajectoire ayant l’allure représentée sur la figure 12 et une dérive perpendiculaire à la fois à B et 暴B².

Les propriétés des orbites adiabatiques que l’on vient de décrire trouvent une illustration complète dans la magnétosphère terrrestre ^{[cf. MAGNÉTOSPHÈRES]}. Dans cette région, située approximativement au-dessus de 1 000 km d’altitude, se trouvent des particules chargées (essentiellement des électrons et des protons) qui sont guidées par le champ magnétique terrestre: elles oscillent (fig. 13) entre deux miroirs magnétiques et font lentement le tour de la Terre en dérivant vers l’est ou vers l’ouest.

Compression magnétique

L’exemple le plus simple de mouvements adiabatiques d’un plasma dans un champ B non statique est fourni par le schéma de la figure 14: on suppose que B est à tout instant uniforme mais croissant lentement avec le temps. Cela peut se réaliser au moyen d’une bobine entourant le plasma; la figure 14 représente une section droite de la bobine et du plasma. Entre les instants t et t 礪 t , un tube de force du champ s’est contracté de T en T . Au champ magnétique variable B est associé, d’après les équations de Maxwell, un champ électrique azimuthal E. Celui-ci produit sur les particules une dérive électrique radiale w^E; l’analyse quantitative de cette dérive montre qu’à l’instant t les particules qui étaient initialement sur le tube T se retrouvent sur T . Autrement dit, la matière et le champ magnétique se déplacent solidairement: cette propriété essentielle est une des bases de la magnétohydrodynamique, discipline qui décrit les mouvements d’un fluide conducteur dans un champ magnétique ^{[cf. MAGNÉTOHYDRODYNAMIQUE]}. L’analyse qui précède montre que son application aux plasmas est limitée aux phénomènes de basse fréquence tels que la condition d’adiabaticité temporelle soit satisfaite pour les ions du plasma ( 諸麗諸^bi ).

Du point de vue pratique, l’expérience de la figure 14 est utilisée pour produire des plasmas denses et chauds: la densité et la température transversale, définie comme la valeur moyenne de (1/2)mw ² size=1^旅, des particules du plasma croissent en effet comme B lors d’une telle «compression magnétique».

4. Plasmas coulombiens

Longueurs fondamentales et classification des plasmas

Pour étudier les interactions entre particules dans un plasma complètement ionisé, on peut introduire les longueurs fondamentales suivantes: ^D, longueur de Debye; d^e , distance moyenne entre électrons; r ⁰, longueur de Landau; l^e , libre parcours moyen des électrons vis-à-vis des «chocs proches».

La signification de^D a déjà été discutée et celle de d^e est évidente. La longueur de Landau, définie par la formule:

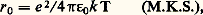
où e est la charge de l’électron, donne l’ordre de grandeur de la distance à laquelle il faut approcher deux électrons pour que leur énergie d’interaction coulombienne soit égale à l’énergie d’agitation thermique. En d’autres termes, c’est l’ordre de grandeur de la distance à laquelle doivent passer deux particules du plasma pour effectuer une collision dite proche, c’est-à-dire à forte déviation, l^e enfin est le libre parcours moyen des électrons entre deux tels «chocs proches».

En comparant les valeurs de ces longueurs fondamentales, et en étudiant les limites de la théorie classique sur laquelle est fondée cette analyse, on peut établir le diagramme de la figure 15 qui permet de classer les plasmas proches de l’équilibre thermodynamique en familles, en fonction de leur densité électronique n^e et de leur température T.

La grande région centrale de ce diagramme correspond à la famille des plasmas cinétiques parfaits , ainsi dénommés parce que leur énergie interne est essentiellement constituée par l’énergie cinétique des particules qu’ils contiennent, ce qui les apparente aux gaz parfaits. Dans cette famille qui comprend la plupart des plasmas usuels, on a entre les longueurs fondamentales les inégalités fortes:

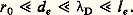
Ces inégalités seraient renversées dans la région des plasmas corrélés caractérisés par une énergie de liaison entre électrons et ions plus forte que leurs énergies cinétiques. En fait, ces plasmas, plus ou moins apparentés aux gaz denses et aux liquides, sont encore mal connus parce qu’ils sont difficiles à produire.

Propriétés générales des plasmas cinétiques

Dans les plasmas cinétiques, ce sont les interactions lointaines entre particules qui dominent la dynamique du milieu. Cela tient au fait que le potentiel de Coulomb qui décrit les interactions binaires entre particules ne décroît que lentement avec la distance. La trajectoire d’un électron dans le plasma a donc l’allure représentée grossièrement sur la figure 16: les collisions proches (A, B) sont des phénomènes binaires relativement rares qui se produisent lorsque l’électron s’approche accidentellement d’une autre particule à une distance r ⁰ 廉 d^e ; elles jouent un rôle moins important que la somme des interactions lointaines et multiples dont l’action sur la trajectoire est représentée par des petites déviations aléatoires. En faisant la statistique de ces petites déviations on peut définir un temps de relaxation moyen t ¹ pour l’échange de quantité de mouvement entre les électrons thermiques et les ions. La quantité 益¹ = 1/t ¹ est la fréquence de collision pour l’échange de quantité de mouvement. On peut essayer de calculer 益¹ en décomposant le phénomène en une suite de collisions binaires lointaines aléatoires; le calcul se ramène à une intégrale sur le paramètre d’impact p de ces collisions (cf. théorie CINÉTIQUE DES FLUIDES); mais on trouve alors que cette intégrale diverge si on laisse tendre le paramètre d’impact maximum vers l’infini. Cette difficulté disparaît si l’on effectue une coupure sur p à une valeur:

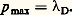
Ce procédé se justifie intuitivement en remarquant que^D est la longueur d’écran au-delà de laquelle les corrélations atténuent exponentiellement le potentiel de Coulomb. On obtient ainsi pour 益¹ (dans un plasma une fois ionisé) les expressions:

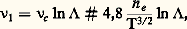
avec:

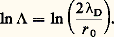
Dans ces formules, 益^c représente la fréquence de collision que l’on aurait avec les seules collisions proches; le facteur ln 炙 est appelé logarithme coulombien . Il précise l’importance des collisions lointaines et est en général beaucoup plus grand que l’unité.

Un plasma cinétique possède donc deux fréquences caractéristiques fondamentales:

– la fréquence d’oscillation de plasma 諸^p ,

– la fréquence de collision 益¹.

En les comparant, on obtient:

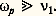
Cette inégalité permet de négliger les collisions dans la description des oscillations de plasma. Le rapport 諸^p / 益¹ est le facteur de qualité (surtension des radioélectriciens) de ces oscillations.

De façon plus générale, un plasma possède deux comportements assez différents selon les échelles de temps considérées.

Aux échelles de temps de l’ordre de 諸^p size=1^漣¹ (perturbations de fréquences caractéristiques voisines de 諸^p ), la dynamique du plasma est dominée par les phénomènes collectifs de charge d’espace. L’équation cinétique qui décrit l’évolution de la fonction de distribution f^e des électrons est alors l’:

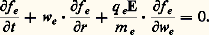
Cette équation est formellement analogue à une équation de Boltzmann sans second membre qui permettrait d’étudier les plasmas sans interactions. Cependant le champ E qui y figure n’est pas un champ d’origine extérieure, mais le champ self-consistant produit par les déséquilibres macroscopiques de charge électrique dans le plasma. L’étude mathématique de l’équation de Vlasov montre que certaines ondes susceptibles de se propager dans le plasma subissent un amortissement spécial non collisionnel connu sous le nom d’amortissement de Landau . L’origine physique de cet amortissement est dans un échange d’énergie «résonant» entre l’onde et les électrons du plasma qui se meuvent en synchronisme avec elle. L’équation de Vlasov permet également d’étudier de nombreux processus d’instabilités, d’interactions non linéaires entre ondes; ces divers mécanismes jouent un rôle très important dans les plasmas «turbulents».

Aux échelles de temps de l’ordre de 益¹ size=1^漣¹ (perturbations de fréquences caractéristiques voisines de 益¹), la dynamique du plasma est dominée par les phénomènes de collisions . L’équation qui décrit l’évolution du plasma est alors plus difficile à établir. Elle a été obtenue sous diverses formes connues sous le nom d’équations de Landau, Fokker-Planck, Rosenbluth, Klimontovitch, Balescu-Lenard-Guernesey. Ces diverses équations montrent que, après un intervalle de temps assez long, un plasma abandonné à lui-même «relaxe» vers l’équilibre thermodynamique. Elles permettent, d’autre part, de calculer les coefficients de transport des plasmas en basse fréquence (coefficients de diffusion, de viscosité, de conductivité électrique et thermique). En particulier, la conductivité électrique 靖 en courant continu est donnée par la formule de Spitzer:

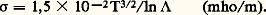
On voit que 靖 devient très grande à haute température: la conductivité des plasmas peut alors atteindre et dépasser celle du cuivre.

5. Propagation d’ondes dans les plasmas

Ondes planes dans un plasma

Les ondes qui se propagent dans les plasmas peuvent être de plusieurs types: des ondes transversales analogues aux ondes électromagnétiques usuelles, des ondes longitudinales analogues aux ondes acoustiques, mais aussi des ondes hybrides. La classification de ces ondes est plus complexe dans les plasmas que dans les autres milieux matériels pour les raisons suivantes:

– un plasma contient deux espèces de particules (électrons et ions) de masses très différentes; selon le type d’onde et le domaine de fréquence considérés, ce peut être l’une, l’autre ou les deux espèces de particules qui participent à l’onde;

– en général, les plasmas sont associés à des champs magnétiques et la présence de ceux-ci leur donne un caractère anisotrope qui leur confère des propriétés de biréfringence plus ou moins analogues à celles des cristaux uniaxes.

Bien entendu, les formes des ondes peuvent être très variées (planes, cylindriques, sphériques, etc.), mais on se limitera aux ondes planes, c’est-à-dire à celles qui se traduisent par des oscillations de toutes les grandeurs physiques de la forme:

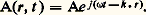
La fréquence angulaire 諸 et le vecteur d’onde k ne sont pas des variables indépendantes; 諸 et k sont reliées par la relation:

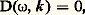
appelée équation de dispersion . Si dans celle-ci on se fixe 諸, on obtient plusieurs solutions pour k; à chacune de ces solutions correspond un mode de propagation.

Plasma sans champ magnétique; fréquence de coupure

Si le champ magnétique est nul, les propriétés de propagation sont les mêmes dans toutes les directions. L’équation de dispersion ne dépend que du module de k et non de son orientation. On trouve d’autre part que D se factorise et peut s’écrire:

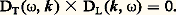
Au facteur D^T sont associées des ondes transversales, et à D^L des ondes longitudinales. Les propriétés de ces ondes se représentent commodément sur des diagrammes de dispersion où l’on porte en abscisse 諸^2p / 諸² et en ordonnée l’indice de propagation:

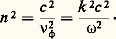
Les figures 17 et 18 représentent les diagrammes de dispersion des ondes transversales et longitudinales. Sur ces diagrammes, les hautes fréquences sont à gauche et les basses à droite.

Les ondes transversales (fig. 17) sont à polarisation rectiligne: toutes les directions de polarisation perpendiculaire à k sont autorisées et correspondent à un même mode de propagation. Ce mode se confond avec les ondes électromagnétiques usuelles à ceci près que, dans les plasmas, la vitesse de phase 益 size=1^﨏 de ces ondes est supérieure à c ; 益 size=1^﨏 tend vers l’infini lorsqu’on se rapproche du point P, c’est-à-dire de la fréquence 諸^p ; au-delà de ce point, k devient imaginaire. Les ondes électromagnétiques qui peuvent se propager dans le plasma sont donc limitées à la bande 諸礪諸^p . Pour les fréquences 諸麗諸^p , on ne peut avoir que des ondes évanescentes rapidement atténuées. On dit que 諸^p est une fréquence de coupure pour les ondes électromagnétiques. Si une onde de fréquence inférieure à la fréquence de coupure arrive sur la frontière d’un plasma en venant de l’extérieur, elle se réfléchit sur cette frontière. Ce phénomène se manifeste dans la propagation des ondes radio autour de la Terre: l’ionosphère y joue, pour les fréquences inférieures à quelques MHz, le rôle de réflecteur .

Les ondes longitudinales correspondent à deux modes, les oscillations de plasma et les ondes pseudosonores.

Les oscillations de plasma se situent dans la gamme de fréquences qui est légèrement supérieure à 諸^p (segment MP sur la figure 18). Dans ce mode, les ions sont pratiquement immobiles et les électrons seuls participent à l’onde. La vitesse de phase peut être supérieure ou inférieure à c , mais en tout cas supérieure à la vitesse d’agitation thermique V^e des électrons; lorsque 益 size=1^﨏 se rapproche de V^e (arc LM), les ondes sont fortement atténuées par l’amortissement de Landau.

Les ondes pseudo-sonores se situent dans la gamme des basses fréquences. Dans ce mode, les électrons et les ions oscillent solidairement. Pour que ce mode puisse se propager sans amortissement de Landau excessif, il faut que la température électronique T^e soit nettement supérieure à Tⁱ . Dans le domaine des fréquences assez basses, la vitesse de phase de ces ondes devient indépendante de la fréquence (asymptote S) et prend la valeur:

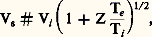
appelée vitesse du son (où Vⁱ est la vitesse d’agitation thermique, Ze étant la charge des ions).

Propagation parallèle à un champ magnétique

Lorsque le plasma est placé dans un champ magnétique, les phénomènes de propagation dépendent de la direction du vecteur k.

En propagation parallèle (k 瑩B), les ondes longitudinales ne sont que très peu affectées par la présence de B. Par contre, les ondes transversales sont profondément modifiées et le plasma devient biréfringent. Les deux modes de propagation permis sont à polarisations circulaires; l’un, mode gauche (souvent appelé «extraordinaire», mais cette dénomination est ambiguë), a son champ électrique tournant dans le sens de la rotation gyromagnétique des électrons; l’autre, mode droit (ou ordinaire), tourne dans le même sens que les ions. Le diagramme de dispersion a alors l’allure représentée sur la figure 19. On y voit apparaître:

– deux coupures (points Q et R);

– deux résonances cyclotron , lorsque la fréquence de l’onde est égale à la fréquence gyromagnétique d’une des espèces de particules ( 諸^be pour le mode gauche, 諸^bi pour le mode droit);

– la limite basse fréquence des ondes d’ Alfvèn ; on montre en magnétohydrodynamique que ces ondes peuvent être assimilées à des vibrations des tubes de force considérés comme des cordes tendues par la tension magnétique; la vitesse de phase correspondante (vitesse d’Alfvèn) est:

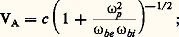
– le domaine dit des siffleurs , ainsi dénommé parce que la propagation de ce mode dans la magnétosphère terrestre permet d’expliquer certains parasites radioélectriques sifflants observés au sol.

Propagation perpendiculaire à un champ magnétique

Enfin, lorsque k est perpendiculaire à B, on a le diagramme de dispersion de la figure 20, où l’on aperçoit:

– le mode dit ordinaire (dénomination ambiguë mais consacrée) dont la polarisation est rectiligne et parallèle à B. Ce mode se propage comme si B était nul (arc IP);

– le mode hybride (arcs IQ, H¹R, H²A) qui présente deux résonances; dans le cas d’un plasma assez dense, les fréquences hybrides haute et basse sont respectivement:

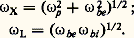
6. Interactions matière-rayonnement

Émission de rayonnement par les plasmas

Les plasmas émettent, comme tous les corps chauds, du rayonnement. Cette émission peut se situer dans n’importe quelle gamme du spectre des ondes électromagnétiques, depuis les ondes radioélectriques jusqu’aux rayons X. La répartition spectrale de ce rayonnement dépend de la densité, du degré d’ionisation et de la température du gaz: lorsque la densité est assez élevée, l’émission devient globalement celle d’un corps noir et il n’est pas nécessaire d’en analyser les mécanismes dans le détail. Mais, en général, les plasmas sont plus ou moins transparents (optiquement minces) au rayonnement qu’ils émettent et l’émission possède des propriétés très différentes de celles d’un corps noir: dans les gaz faiblement ionisés, on observe des spectres de raies dus aux transitions des électrons liés aux atomes; dans les plasmas complètement ionisés, le rayonnement est dû aux transitions entre deux états libres (transitions free-free ) et sa croissance avec la température est moins rapide que celle du corps noir.

Le rayonnement des électrons libres d’un plasma peut s’analyser à partir de la théorie classique de l’électromagnétisme relativiste. On y montre qu’un électron rayonne de l’énergie toutes les fois qu’il est accéléré, et que, si sa vitesse est nettement inférieure à c , la puissance P(t ) émise à l’instant t est donnée par la formule de Larmor:

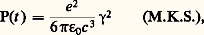
où 塚 est l’accélération de l’électron.

Dans les plasmas, les accélérations subies par les électrons peuvent être de deux natures, magnétique et collisionnelle.

L’accélération magnétique est liée à la présence d’un champ d’induction magnétique B et est produite par la force de Lorentz associée e w 廬 B. Le rayonnement correspondant est le rayonnement cyclotron (ou gyromagnétique). Si la vitesse des électrons du plasma est nettement inférieure à c , c’est-à-dire, en pratique, si k T^e /m^ec ² 廉 1 (plasmas non relativistes), ce rayonnement se déduit de la formule de Larmor. Il se produit à la fréquence gyromagnétique 諸^be et, en l’absence d’autoabsorption (plasma assez mince), la puissance P^c rayonnée par unité de volume du plasma est:

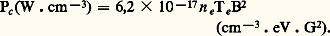
Dans les plasmas relativistes qui existent dans certaines régions de l’Univers, les propriétés de ce rayonnement changent notablement: le principal effet est une émission sur des harmoniques parfois d’ordre très élevé de la fréquence 諸^be ; c’est ce qu’on appelle alors le rayonnement synchrotron , par référence aux accélérateurs d’électrons qui permettent de l’observer en laboratoire.

L’accélération collisionnelle se produit lorsqu’un électron effectue une collision avec une autre particule du plasma. Le rayonnement correspondant est le Bremsstrahlung (rayonnement de freinage): son spectre est toujours continu. Dans les gaz faiblement ionisés, c’est un petit effet dû aux collisions élastiques électron-neutre. Dans les plasmas complètement ionisés, il est produit par les interactions électron-ion; c’est alors très souvent le mécanisme dominant de rayonnement et il conduit, pour un plasma optiquement mince, à la puissance d’émission suivante par unité de volume:

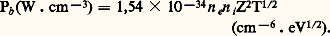
On voit que la puissance émise par Bremsstrahlung est proportionnelle au carré de la charge Ze des ions et peut donc devenir particulièrement importante dans les plasmas d’éléments lourds multiplement ionisés.

Interactions entre photons et matière

Dans les plasmas assez denses, les mécanismes d’émission spontanée sont compliqués par les phénomènes de diffusion, d’absorption et d’émission stimulée. Il est alors souvent utile de considérer le rayonnement comme un gaz de photons constituant une nouvelle espèce de particules en interaction avec les particules matérielles (électrons, ions, atomes).

Les principales interactions à considérer sont celles des photons avec les électrons, à savoir: la diffusion Compton (phénomène de collision élastique entre un photon et un électron) et l’absorption par Bremsstrahlung «inverse». C’est une collision inélastique entre un photon et un électron dans le champ d’un ion; dans cette interaction, le photon disparaît, et son énergie est transférée essentiellement à l’électron bien que la présence de l’ion soit nécessaire pour satisfaire les théorèmes de conservation de la mécanique.

Dans les plasmas proches de l’équilibre thermodynamique, les fonctions de distribution f^e des vitesses électroniques et f size=1^益 des quantités de mouvement photoniques sont approximativement connues (distributions de Maxwell et de Planck); on peut alors définir, pour les interactions entre photon et électron et en s’inspirant du modèle de Lorentz – le photon joue ici le rôle de la particule légère –, les trois longueurs d’interaction suivantes entre photons et électrons:

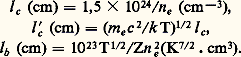
Les deux premières sont deux longueurs moyennes d’interaction Compton, l^c relative aux échanges de quantité de mouvement, et l ^c 拾 l^c aux échanges d’énergie; l^b est la longueur moyenne d’interaction par Bremsstrahlung inverse. En comparant les valeurs de ces longueurs, on peut compléter la classification des plasmas dans le diagramme (n^e T^e ). On obtient ainsi la figure 21, tracée pour l’hydrogène, où l’on voit apparaître dans la famille des plasmas cinétiques assez denses les zones B, BC et C.

Dans la zone B, relative aux plasmas matériels à interaction par Bremsstrahlung (assez forte densité, pas trop haute température), le libre parcours moyen des photons est la longueur l^b d’interaction par Bremsstrahlung . On montre d’ailleurs que l’énergie interne du plasma est essentiellement l’énergie cinétique des particules matérielles.

Dans la zone BC (plasmas radiatifs à électrons couplés aux ions), le libre parcours moyen des photons est maintenant la longueur l^c d’interaction Compton. L’énergie interne du milieu est essentiellement radiative. Cependant, la densité d’énergie radiative n’étant pas très élevée (gamme moyenne de températures), les électrons sont plus fortement liés aux ions qu’au rayonnement.

Dans la zone C (plasmas radiatifs à électrons couplés au rayonnement), le libre parcours moyen des photons est toujours déterminé par l’effet Compton, mais la densité d’énergie radiative, qui croît comme ⁴, est maintenant si élevée que les électrons sont plus fortement couplés au rayonnement qu’aux ions.

On peut d’ailleurs vérifier que, dans tous les cas, les longueurs d’interaction l^ee 力 l^ei des électrons entre eux ou avec les ions sont plus courtes que les longueurs d’interaction des photons avec la matière. Si donc les dimensions caractéristiques d’un plasma sont supérieures à l^ee , mais inférieures à la plus petite des longueurs l^b et l ^c , il y a équilibre thermique local de la matière, mais aucun équilibre entre matière et rayonnement. La classification établie selon les zones B, CB, C n’a donc de sens que si les dimensions du plasma sont supérieures à la longueur d’interaction des photons. Les trajets M N P et MNP étant les lieux où cette longueur l size=1^﨏 sur la figure 21 est égale à 1 mm ou à 10 m, on peut dire que MNP marque la limite des plasmas que l’on peut observer en équilibre thermodynamique à l’échelle terrestre.

7. Réactions nucléaires dans les plasmas de haute température

Réactions de fusion des noyaux légers

Dans un plasma de température très élevée (face=F0019 礪 10⁶ K), les atomes sont ionisés de multiples fois. À la limite, on tend vers un milieu composé d’électrons libres et de noyaux débarrassés de tout leur cortège électronique. Dans ces conditions, les noyaux interagissent, d’une part, grâce à la force répulsive coulombienne, mais d’autre part, grâce aux forces à courte portée dites nucléaires. Si donc deux noyaux s’approchent assez près l’un de l’autre, ils peuvent produire une réaction nucléaire. Pour cela, il faut que leur vitesse relative initiale soit assez grande pour permettre de surmonter la «barrière» de potentiel coulombienne. On vérifie, de ce fait, que les diverses réactions entre deux noyaux ont des sections efficaces qui deviennent très faibles aux basses énergies. En pratique, on trouve que les réactions nucléaires ne se produisent de façon notable dans les plasmas que si leur température est supérieure à 1 keV (c’est-à-dire environ 10⁷ K; dans la gamme considérée, on a l’habitude de mesurer les températures par la valeur de k T mesurée en eV). Si la température reste dans la gamme 1 keV-1 MeV, les seules réactions susceptibles de se produire sont les réactions exothermiques qui conduisent à des noyaux plus stables que les noyaux initiaux. Les plus importantes sont les réactions de «fusion» des noyaux légers qui conduisent finalement au noyau très stable He⁴, soit:

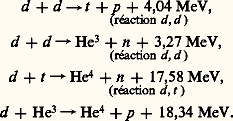
La figure 22 montre comment varient en fonction de l’énergie (dans le système du centre de masse) les sections efficaces des réactions (d , d ) et (d , t ). En partant de ces courbes, on peut calculer les puissances nucléaires P^N produites par centimètre cube dans les plasmas de deutérium pur ou mélangé à du tritium. Dans le deutérium pur, on trouve:

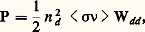
où n ^d est la densité numérique du deutérium, W^dd = 4,04 MeV et 麗靖益礪 varie avec la température comme indiqué sur la figure 23. Pour T voisin de 40 keV et un plasma de densité 2,6 憐10¹⁹ (densité normale d’un gaz parfait), P^N serait de l’ordre de 10⁹ W/cm³.

Réacteurs nucléaires à «fusion contrôlée»

Les réactions de fusion des noyaux légers dans un plasma très chaud peuvent donc être une source d’énergie très importante. Cette source est effectivement utilisée dans les

bombes H (cf. énergie THERMONUCLÉAIRE). Il est très intéressant de pouvoir l’employer à la production d’énergie électrique dans des réacteurs fonctionnant de façon «contrôlée», c’est-à-dire non explosive. On dispose alors de ressources en énergie quasiment illimitées à l’échelle humaine, puisque la matière première est le deutérium contenu dans l’eau des océans, à raison de 1,6 g/l.

La réalisation d’un réacteur à fusion contrôlée fait l’objet de recherches entreprises dans les grands pays depuis les années 1950. Dans la première génération de réacteurs de fusion, le combustible sera un mélange deutérium-tritium (le tritium étant un isotope radioactif de l’hydrogène). Le deutérium pur serait plus intéressant parce que naturellement abondant, mais il conduit à des conditions de fonctionnement plus difficiles à réaliser que celles du mélange D-T: température nécessaire de l’ordre de 100 à 200 millions de degrés. Le tritium n’existant pas à l’état naturel, il faut le synthétiser. Dans un réacteur de fusion, ce processus a lieu dans un bouclier extérieur contenant du lithium 6 selon la réaction:

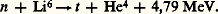
Si l’on veut amorcer dans le plasma une réaction en chaîne, il faut à première vue se placer dans des conditions où la puissance nucléaire P^N est supérieure à la puissance P^B rayonnée par Bremsstrahlung , ce qui conduit à une condition T 礪 T^c sur la température (T^c est la température critique de Post), respectivement pour d , d et d , t :

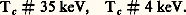
En fait, le problème doit être posé en considérant le bilan d’énergie d’un réacteur dans lequel le plasma de densité n et de température T séjourne pendant un temps 精, et l’on obtient alors un critère établi par Lawson qui définit, en fonction de T, la valeur du produit n 精 à réaliser. La figure 24 montre les résultats d’un tel calcul; 兀 est un rendement pratique de transformation de l’énergie. Si l’on prend pour ce paramètre la valeur 1/3 plutôt optimiste proposée par Lawson, on obtient comme conditions minimales de fonctionnement d’un réacteur, respectivement pour d , d et d , t :

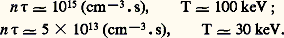
Pour réaliser ces conditions, on a donc à résoudre deux problèmes plus ou moins liés: chauffage d’une certaine quantité de matière à des températures très élevées; «confinement» destiné à maintenir dans un certain volume le plasma ainsi formé avec une densité n et une durée de vie 精 aussi élevées que possible.

Le chauffage peut s’effectuer par effet Joule (passage d’un courant très intense), irradiation laser (focalisation d’un laser de très grande puissance sur un grain de matière solide) ou par des méthodes propres aux plasmas (compression magnétique, résonances d’ondes par exemple).

En ce qui concerne le confinement inertiel , certains auteurs cherchent à réaliser le produit n 精 nécessaire avec une force valeur de n et une durée de vie 精 assez courte (face=F0019 麗 10 size=1^漣⁶ s). C’est la solution dite fusion rapide qui est associée au chauffage par des lasers intenses ou des faisceaux de particules. Le confinement du plasma (mélange deutérium-tritium) très dense peut être assuré par la matière lancée à grande vitesse; cette expérience peut avoir lieu plusieurs fois par seconde.

Confinement magnétique d’un plasma

Cependant, la plupart des physiciens de la fusion contrôlée ont concentré leurs efforts de recherche dans le domaine de la fusion par confinement magnétique ; dans ce cas, le produit n 精 nécessaire avec des valeurs de n relativement faibles (de 2 à 3 憐 10²⁰ m size=1^漣³) et des valeurs du temps de confinement 精 aussi grandes que possibles (par exemple, n 力 10¹⁴ cm³, 精力 1 s).

Compte tenu de la température extrêmement élevée du plasma, celui-ci doit donc être isolé de toute paroi matérielle. La seule solution qui semble possible est alors le confinement magnétique qui utilise des champs magnétiques de structure appropriée. L’idée de départ (fig. 8) est que, dans un champ magnétique B suffisamment intense, les particules se déplacent en spirales autour des lignes de forces de B et ne peuvent donc pas diffuser dans les directions perpendiculaires à B. Le champ magnétique semble donc fournir un parfait moyen de confinement transversal : une analyse détaillée montre cependant que le confinement transverse est limité par un effet de diamagnétisme du plasma. L’ensemble des mouvements giratoires des particules produit (fig. 25), à la périphérie d’un volume de plasma confiné magnétiquement, un courant macroscopique qui crée un champ magnétique B^p opposé au champ B d’origine extérieure. L’importance de ce diamagnétisme est mesurée par le rapport:

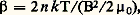
qu’on peut considérer ^{[cf. MAGNÉTOHYDRODYNAMIQUE]} comme le rapport entre la pression matérielle 2 nk T du plasma et la pression magnétique B²/2 猪⁰.

Lorsque ce rapport 廓 tend vers l’unité, le plasma ne peut plus être confiné.

Il est évident, d’autre part, qu’un champ B uniforme n’assure aucun confinement longitudinal. Pour tourner cette difficulté, on peut utiliser l’effet de miroir magnétique produit par des tubes de forces convergents (champ croissant vers les extrémités du dispositif) ou simplement refermer le système sur lui-même dans une configuration à topologie torique .

Cependant, de nombreuses études expérimentales ou théoriques ont montré que l’équilibre d’un plasma confiné magnétiquement est généralement instable. Certaines instabilités , dites macroscopiques, se décrivent par les équations hydrodynamiques et se traduisent par des déformations de la surface extérieure du plasma. D’autres, dites microscopiques, dépendent de la forme détaillée des fonctions de distribution et se traduisent par l’apparition d’oscillations dans le plasma et d’une turbulence qui permet une diffusion transverse du plasma.

Pour vaincre ces instabilités, les spécialistes de la fusion ont imaginé des formes complexes de champ magnétique qui conduisent à divers types de machines à plasma (Stellarators; pinch toroïdaux, Tokamak, etc.). Au cours de ces études longues et difficiles, les valeurs de T et n 精 réalisées n’ont cessé de progresser; cependant (fig. 26) on est encore, assez loin du but poursuivi (cf. énergie THERMONUCLÉAIRE).

Encyclopédie Universelle. 2012.