Akademik

отделимое топологическое векторное пространство над полем действительных или комплексных чисел, в к-ром любая окрестность нулевого элемента содержит выпуклую окрестность нулевого элемента; иначе говоря, топологическое векторное пространство Етогда и только тогда есть Л. в. п., когда топология в Еесть отделимая локально выпуклая топология. Примерами Л. в. п. (и одновременно важными в теории и приложениях классами Л. в. п.) являются нормированные пространства, счетно нормированные пространства, Фреше пространства.

Ряд общих свойств Л. в. п. непосредственно следует из соответствующих свойств локально выпуклых топологий; в частности, подпространства и отделимые факторпространства Л. в. п., а также произведения семейств Л. в. п. суть Л. в. п. Пусть А- направленное вверх множество индексов, - семейство Л. в. п. (над одним и тем же полем) с топологиями 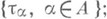пусть для любой пары определено непрерывное линейное отображение g_ab: и пусть Е - подпространство произведения элементы к-рого х= (х _a). удовлетворяют соотношениям 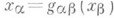для всех пространство Еназ. проективным пределом семейства {Е_a} относительно отображений {g_ab} и обозначается lim g_abE_b;. топология в Еесть проективная топология относительно семейства где f_a - ограничение на подпространство Епроекции С другой стороны, пусть для любой пары определено непрерывное линейное отображение пусть - канонич. вложение пространства Е _a. в прямую сумму и Н - подпространство в порожденное образами всех пространств Е _a. при отображениях где (а, Р) пробегает все пары в для к-рых Если Нзамкнуто в то Л. в. п. наз. индуктивным пределом семейства Л. в. п. {Е_a} относительно отображений {h_ab} и обозначается lim h_abE_a. Если {Е_a} есть семейство подпространств векторного пространства Е, упорядоченное по включению, и топология t_b индуцирует t_a на Еа при то индуктивный предел семейства {Е_a} наз. строгим. Л. в. п. метризуемо в том и только в том случае, когда его топология порождена последовательностью полунорм; Л. в. п. нормируемо тогда и только тогда, когда в нем существует ограниченное открытое множество (теорема Колмогорова). Всякое конечномерное подпространство в Л. в. п. имеет дополнительное замкнутое подпространство. Пополнение Л. в. п. есть Л. в. п., и всякое полное Л. в. п. изоморфно проективному пределу некоторого семейства банаховых пространств. Пространство L(F, E).непрерывных линейных отображений топологического векторного пространства Fв Л. в. п. Еестественно снабжается структурой Л. в. п. (см. также Операторная топология).по данному семейству ограниченных подмножеств пространства F, линейная оболочка объединения к-рых плотна в F:базис окрестностей нуля соответствующей топологии есть семейство множеств где s пробегает семейство а Vпробегает базу окрестностей нуля в Е.

Центральное место и основное содержание теории не только Л. в. п., но и топологических векторных пространств составляет изучение Л. в. п. в терминах его сопряженного пространства. Фундаментом этой теории двойственности для Л. в. п. является Хана-Банаха теорема, из к-рой, в частности, следует, что если Е - Л. в. п., то его сопряженное пространство Е' разделяет точки пространства Е.

Существенной частью теории Л. в. п. является теория компактных выпуклых множеств в Л. в. п. Выпуклая оболочка со Ки выпуклая закругленная оболочка предкомпактного множества Кв Л. в. п. Епредкомпактны; если Е, кроме того, квазиполно, то замкнутая выпуклая оболочка Кмножества Ки его замкнутая выпуклая закругленная оболочка компактны. Если А, К непересекающиеся непустые выпуклые подмножества в Л. в. п. Е, причем Азамкнуто, а Ккомпактно, то существует такой непрерывный действительный линейный функционал f на Е, что для нек-рого действительного а неравенства выполняются для всех соответственно; в частности, любое непустое замкнутое выпуклое множество А в Л. в. п. есть пересечение всех содержащих его замкнутых полупространств. Непустое замкнутое выпуклое подмножество Взамкнутого выпуклого множества Апаз. гранью множества А, если любой замкнутый отрезок в Л, внутренняя точка к-рого содержится в В, целиком лежит в В;точка наз. крайней точкой множества А, если множество {х} является гранью в А. Если К - компактное выпуклое множество в Л. в. п. E и дК - множество его крайних точек, то для множества следующие условия эквивалентны: 1) 3)sup f(X)=sup f(K).для любого непрерывного действительного линейного функционала f на Е. В частности, дК= К (теорема К р е й н а - М и л ь м а н а). Множество дК является бэровским пространством в индуцированной топологии (т. е. пересечение любой последовательности плотных в дК открытых подмножеств дК плотно в дК), и для любого существует такая вероятностная мера m на К, что

и мера р, обращается в нуль на всех бэровских подмножествах не пересекаюгцихся с дК (а если Кметризуемо, то m( дК) = 1). Всякое непрерывное отображение компактного выпуклого множества Кв Л. в. п. в себя имеет неподвижную точку (теорема Шаудера - Тихонова); коммутативное семейство непрерывных аффинных преобразований множества Кв себя (и равностепенная непрерывная группа непрерывных аффинных преобразований Кв себя) имеет неподвижную точку. "

Еще один важный раздел теории Л. в. п.- теория линейных операторов в Л. в. п.; в частности - теория компактных (наз. также вполне непрерывными), ядерных и фредгольмовых операторов. Теоремы о замкнутом графике и открытом отображении имеют в теории Л. в. п. далеко идущие обобщения. Л. в. п. Еназ. обладающим свойством аппроксимации, если тождественное отображение пространства Ев себя может быть равномерно аппроксимировано на предкомпактных множествах в Еконечномерными непрерывными линейными отображениями пространства Е в себя; если Л. в. п. обладает свойством аппроксимации, то оно обладает рядом других замечательных свойств и, в частности, в таком пространстве любой ядерный оператор имеет однозначно определенный след. Существуют сепарабельные банаховы пространства, не обладающие свойством аппроксимации, но банаховы пространства с базисом Шаудера и подпространства проективных пределов гильбертовых пространств обладают свойством аппроксимации. Некоторые варианты этого свойства представляют интерес в теории вполне непрерывных операторов и теории операторов Фредгольма.

Заметную роль в теории Л. в. п. играют методы гомологич. алгебры, связанные с изучением категории Л. в. п. и их непрерывных отображений, а также нек-рых подкатегорий этой категории. В частности, гомо-логич. методы позволили решить ряд задач, связанных с продолжением линейных отображений, с существованием линейного отображения в данное пространство, накрывающего отображение в факторпространство этого пространства, а также изучить свойства пополнений факторпространств E/F в связи с пополнением пространств Еи F.

Другими существенными вопросами теории Л. в. п. являются: теория интегрирования вектор-функций со значениями в Л. в. п. (как правило, бочечном пространстве); теория дифференцирования нелинейных отображений Л. в. п.; теория топологических тензорных произведений Л. в. п. и связанная с ними теория операторов Фредгольма, ядерных операторов н ядерных пространств. Существует содержательная теория ряда специальных классов Л. в. п. таких, как бочечные пространства, борнологич. пространства (на к-рых любая полунорма, ограниченная на ограниченных множествах, непрерывна), рефлексивные и полурефлексивные пространства (канонич. отображение к-рых в сильное второе сопряженное пространство является соответственно топологическим или линейным изоморфизмом), ядерные пространства и т. д.

Лит.:[1] Колмогоров А. Н., "Studia math.", 1934, t. 5, p. 29-33; [2] Б у р б а к и Н., Топологические векторные пространства, пер. с франц., М., 1959; [3] его ж е, Интегрирование, пер. с франц., М., 1970, гл. 6-8; то же, 1977, гл. 3-5, 9; [4] Ш е ф е р X., Топологические векторные пространства, пер. с англ., М., 1971; [5] Дэй М. М., Нормированные линейные пространства, пер. с англ., М., 1961; [6] Д а н ф о р д Н., Шварц Д ж., Линейные операторы. Общая теория, пер. с англ., М., 1962; [7] Пич А., Ядерные локально выпуклые пространства, пер. с нем., М., 1967; [8] Робертсон А.-П., Робертсон В.-Дж., Топологические векторные пространства, пер. с англ., М., 1967; [9] Ф е л п с Р., Лекции о теоремах Шоке, пер. с англ., М., 1968; [10] Э н ф л о П., "Математика", 1974, т. 18, № 1, с. 146-55; [11] Фрёлихер А., Бухер В., Дифференциальное исчисление в векторных пространствах без нормы, пер. с англ., М., 1970; [12] Паламодов В. П., "Успехи матем. наук", 1971, т. 2G, в. 1, с. 3-65.

А. II. Штерн.