- ФОРМФАКТОР
-
злектромагнитный, ф-ция, характеризующая пространств. распределение заряда (электрич. Ф.) или магн. момента (магн. Ф.) внутри атома, ат. ядра или элем. ч-цы. Хар-р этого распределения (его размеры и плотность) определяется типом ч-ц, образующих данную систему, и их вз-ствием. Так, Ф. атома определяется распределением ат. эл-нов, а ср. радиус этого распределения порядка 10-8 см. Ф. ат. ядра определяется в основном распределением нуклонов в ядре, ср. радиус к-рого =10-12 см. Ф. адронов, согласно совр. представлениям, определяется распределением «цветных» кварков внутри адрона и характеризуется размером порядка т. н. радиуса удержания «цвета», величина к-рого равна прибл. 10-13 см.В отличие от этого, ср. радиус Ф. эл-наопределяется облаком виртуальных электрон-позитронных пар. Несмотря на довольно большую протяжённость облака ( »?0a, где?0= 10-11 см — комптоновская длина волны эл-на, а a»1/137 — постоянная тонкой структуры), в нём заключено всего лишь ок. 1% заряда эл-на, т. к. вероятность рождения виртуальной пары пропорц. a. По этой причине эл-ны (а также мюоны) можно с хорошей точностью рассматривать как бесструктурные (точечные) ч-цы. Экспериментально Ф. измеряется с помощью упругого рассеяния эл-нов (или мюонов) на соответствующих объектах. При этом за величину Ф. принимается множитель, отличающий величину амплитуды рассеяния при данной передаче импульса от амплитуды рассеяния на точечном объекте. Согласно неопределённостей соотношению, чем больше передача импульса, тем меньше расстояние, на к-ром измеряется Ф.Измерение Ф. адронов при большой передаче импульса (q->1 ГэВ/с) позволяет установить число точечных кварков, составляющих адрон: чем больше этих составляющих (n), тем труднее передать им всем примерно одинаковый импульс, не развалив всей системы, тем быстрее падает Ф. F с увеличением импульса, F=q-2(n-1) (т. н. правила кваркового счёта). Таким путём было получено подтверждение, что протон состоит из трёх кварков (Fр=q-4), а p-мезон — из кварка и антикварка (Fp=q-2). Изучение Ф. дейтрона даёт основание считать, что неск. процентов времени дейтрон проводит не в виде нейтрона и протона, а в виде шестикварковой ч-цы.Аналогично Ф. в упругом рассеянии можно определить Ф. в глубоко неупругих процессах. Их называют обычно структурными функциями. В общем случае структурные ф-ции должны зависеть от двух переменных: квадрата переданного импульса (q2) и энергии, переданной адронам (?адр). Однако, как показывает опыт, эти переменные входят в безразмерной комбинации (см. МАСШТАБНАЯ ИНВАРИАНТНОСТЬ СКЕЙЛИНГ БЬЁРКЕНА). Такое поведение структурных ф-ций можно объяснить, считая, что внутри адронов находятся точечные заряж. ч-цы, названные Р. Фейнманом партонами. Эксперим. данные указывают на то, что в кач-ве партонов выступают кварки. Наличие внутри адронов точечных объектов приводит к слабой зависимости сечения глубоко неупругих процессов от переданного импульса при фиксированном отношении q2/?адр (впервые на возможность такого поведения сечения указал М. А. Марков в 1956).По аналогии с эл.-магн. Ф. определяют слабые Ф., характеризующие слабое вз-ствие лептонов с адронами, напр. распад К+®e++ne+p0 и процесс nm+n®m-+p («упругий» Ф.) или nm+n®m-+адроны (неупругий Ф.). Поскольку в слабом вз-ствии, в отличие от электромагнитного, участвуют не только векторные, но и аксиальные токи, в слабых процессах возникают соответственно векторные и аксиальные слабые Ф. (а также члены, отвечающие их интерференции). Поведение слабых векторных Ф. подобно поведению электромагнитных Ф. (см. ВЕКТОРНОГО ТОКА СОХРАНЕНИЕ).
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ФОРМФАКТОР
-
в т е о р и и э л е м е н т а р н ы х ч а с т и ц - ф-ция, описывающая влияние протяжённости частицы на её взаимодействие с др. частицами и полями. Термин "Ф." заимствован из теории рассеяния рентг. лучей (см. Атомный фактор), а его применение основано на наглядном представлении о том, что, напр., протон проводит часть времени в виртуальном состоянии "нейтрон +p+ -мезон". Поэтому его заряд оказывается "размазанным" с нек-рой плотностью еr(r). Тогда, напр., амплитуда рассеяния электрона на таком размазанном протоне отличается от амплитуды рассеяния на точечном протоне множителем, называемом Ф. протона:
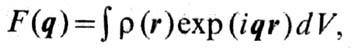
где q- передаваемый при рассеянии импульс.
В последоват. релятивистской локальной теории реальное размазывание невозможно, а строгий смысл термина Ф. в ней определяется следующим образом. Плотность энергии взаимодействия эл.-магн. поля, описываемого 4-потенциалом Am(x) , со свободным фермионом, волновая ф-ция к-рого Y(x), имеет вид
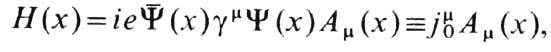
где gm- Дирака матрицы, черта означает дираковское сопряжение, а j0m наз. электромагнитным током свободных фермионов. Но само взаимодействие меняет оператор тока j0m. Матричный элемент эл.-магн. тока взаимодействующего протона, взятый между состояниями реального протона с 4-импульсами р и р', с учётом релятивистской инвариантности, Дирака уравнения и сохранения заряда, в общем случае можно записать в виде
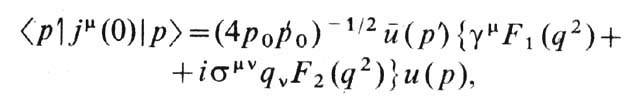
где q=p-p', smv=(i/2)(gmgv-gvgm). Входящие сюда ф-ции F1(q2 )и F2(q2 )наз. электрич. и магн. Ф. протона; о них заранее можно утверждать лишь то, что в пределе q->0, для длинных волн или малых передаваемых импульсов, F1 (0) = е, где е - наблюдаемый заряд, а
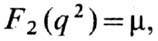где m -полный магн. момент протона. Для свободной частицы 
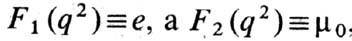, где m0-"нормальный" магн. момент дираковской частицы с зарядом 
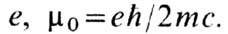В системе координат, где q0 = 0, выражения 
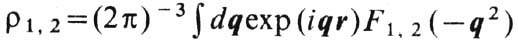можно считать пространств. распределениями соответственно заряда и магн. момента взаимодействующей частицы. Благодаря Ф. F1 и F2. взаимодействующий протон выглядит протяжённым; однако нельзя говорить о реальном физ. размазывании протона, поскольку взаимодействующий ток остаётся локальным оператором и условие микропричинности не нарушается. Аналогично эл.-магн. Ф. F1 и F2 можно ввести мезонные Ф. нуклона, описывающие соответствующий эффект при взаимодействии реального нуклона с мезон-ным полем, и др. Ф.
В нелокальной квантовой теории поля Ф. описывает реальное размазывание частицы. В этом случае плотность энергии взаимодействия фермиона с эл.-магн. полем записывается в виде
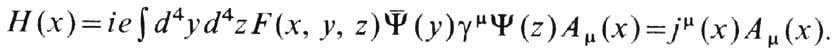
Релятивистски инвариантная ф-ция F(x, y, z)=f[(x-y),(x-z)] наз. Ф. в x -представлении, а её фурье-образ
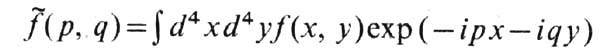
наз. Ф. в p -представлении, или обрезающим множителем. Благодаря Ф. взаимодействие размазано по всей области, где
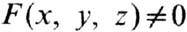. С одной стороны, это приводит к нарушению микропричинности, с другой - подходящий выбор убывания 
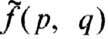при больших значениях её аргументов позволяет устранить ультрафиолетовые расходимости, присущие локальной теории. Для точечного взаимодействия
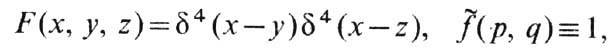
а ток jm(x) превращается в j0m(x )-ток свободных частиц в локальной теории. В. П. Павлов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.