Akademik

СПЕКТР ЭЛЕКТРОМАГНИТНЫХ ВОЛН

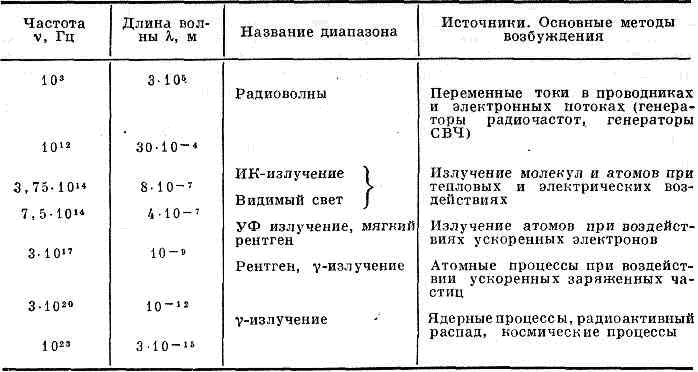Теория Максвелла позволила установить, что радиоволны, свет, рентгеновское и гамма-излучения представляют собой Э. в. с различной длиной волны l (см. табл.), причём между соседними диапазонами шкалы Э. в. нет резких границ (рис.). Частота w колебаний связанных электрич. Е и магнитного Н полей связана с l соотношением: l=c/w.

Особенности Э. в., законы их возбуждения и распространения описываются Максвелла уравнениями. Если в какой-то области пр-ва существуют электрич. заряды е и токи I, то изменение их. со временем t приводит к излучению Э. в. На характер распространения Э. в. существенно влияет среда, в к-рой они распространяются.

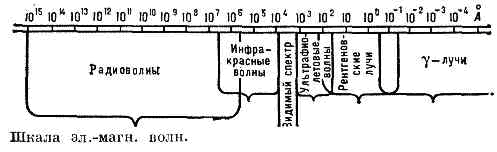Э. в. могут испытывать преломление, в реальных средах имеет место дисперсия волн, вблизи неоднородностей наблюдаются дифракция волн, интерференция волн, полное внутреннее отражение и др. явления, свойственные волнам любой природы. Пространств. распределение эл.-магн. полей, временные зависимости E(t) и H(t), определяющие тип волн (плоские, сферические и др.), вид поляризации и др. особенности Э. в. задаются, с одной стороны, хар-ром источника излучения, с другой -св-вами среды, в к-рой они распространяются. В случае однородной и изотропной среды вдали от зарядов и токов, создающих эл.-магн. поле, ур-ния Максвелла приводят к волновым уравнениям

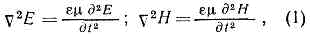описывающим, в частности, распространение плоских монохроматич. Э. в.:

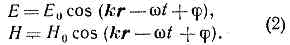Здесь e — диэлектрическая, m — магн. проницаемости среды, Е0 и H0 — амплитуды колебаний электрич. и магнит. полей, w=2pn — круговая частота этих колебаний, j — произвольный сдвиг фазы, k — волновой вектор, r — радиус-вектор точки; N — оператор Лапласа

(E^H^ k, H0 =O(e/m)E0).

Если среда неоднородна или содержит поверхности, на к-рых изменяются её электрич. либо магн. св-ва, или если в пр-ве имеются проводники, то тип возбуждаемых и распространяющихся Э. в. может существенно отличаться от плоской линейно поляризованной волны. Э. в. могут распространяться вдоль направляющих поверхностей (поверхностные волны), в передающих линиях, в полостях, образованных хорошо проводящими стенками (см. РАДИОВОЛНОВОДЫ, СВЕТОВОД), в квазиоптич. линиях (см. КВАЗИОПТИКА).

Хар-р изменения во времени Е и Н определяется законами изменения тока I(t) и зарядов e(t), возбуждающих Э. в. Однако форма волны в общем случае не следует I (t) или e(t). Она в точности повторяет форму тока только в случае линейной среды, если I=I0sinwt. Т. к. волны любой формы можно представить в виде суммы гармонических составляющих, то для линейных сред, для которых справедлив суперпозиции принцип, все задачи излучения, распространения и поглощения Э. в. произвольной формы сводятся к решению задач для гармонич. Э. в. В изотропном пр-ве скорость распространения гармонич. Э. в., т. е. фазовая скорость v=cO(me). При наличии дисперсии скорость переноса энергии vгр (групповая скорость) может отличаться от v. Плотность потока энергии, переносимой Э. в., определяется Пойнтинга вектором

S= (c/4p)(EH).

Т. к. в изотропной среде векторы Е, Н и k образуют правовинтовую систему, то S совпадает с направлением распространения Э. в. В анизотропной среде (в т. ч. вблизи проводящих поверхностей) S может не совпадать с направлением распространения Э. в.

Простейшим излучателем Э. в. явл. электрич. диполь — отрезок проводника длиной 1-l по к-рому протекает ток i=i0 sinwt. На расстоянии от диполя r->l образуется волновая зона (зона излучения), где распространяются сферич. волны (см. АНТЕННА).

Создание мощных источников радиоволн во всех диапазонах, а также появление квантовых генераторов, в частности лазеров, позволило достичь напряжённости электрич. поля в Э. в., существенно изменяющих св-ва сред, в к-рых происходит их распространение. Это привело к развитию нелинейной теории Э. в. При распространении Э. в. в нелинейной среде (e и m зависят от Е и Н) её форма изменяется. Если дисперсия мала, то по мере распространения Э. в. они обогащаются высшими гармониками и их форма постепенно искажается (см. НЕЛИНЕЙНАЯ ОПТИКА). Напр., после прохождения синусоидальной Э. в. характерного пути (величина к-рого определяется степенью нелинейности среды) может сформироваться ударная волна, характеризующаяся резкими изменениями Е и Н (разрывами) с их послед. плавным возвращением к первонач. величинам. Большинство нелинейных сред, в к-рых Э. в. распространяются без сильного поглощения, обладает значит. дисперсией, препятствующей образованию ударных Э. в. Поэтому образование ударных волн возможно лишь в диапазоне X от неск. см до длинных волн. При наличии дисперсии в нелинейной среде возникающие высшие гармоники распространяются с разл. скоростью, и существ. искажения формы исходной волны не происходит. Образование интенсивных гармоник и вз-ствие их с исходной волной может иметь место лишь при специально подобранных законах дисперсии (см. ПАРАМЕТРИЧЕСКИЙ ГЕНЕРАТОР СВЕТА).

Э. в. разл. диапазонов l характеризуются разл. способами возбуждения и регистрации. Они по-разному взаимодействуют с в-вом. Процессы излучения и поглощения Э. в. от самых длинных волн до инфракрасного излучения достаточно полно описываются соотношениями электродинамики. На более высоких частотах доминируют процессы, имеющие существенно квантовую природу, а в оптич. диапазоне и тем более в диапазонах рентгеновских и g-лучей излучение и поглощение Э. в. могут быть описаны только на основе представлений о дискретности этих процессов. Во многих случаях эл.-магн. излучение ведёт себя не как набор монохроматич. Э. в. с частотой w и волн. вектором k, а как поток квазичастиц — фотонов с энергией ћw и импульсом p=ћw/c. Волн. св-ва проявляются, напр., в явлениях дифракции и интерференции, корпускулярные — в фотоэффекте и Комптона эффекте..