GAMME
Il est difficile de donner du mot «gamme» une définition qui soit à la fois exacte et complète, tant sont diverses les notions que ce vocable recouvre et variés, au cours des époques, les objets qu’il désigne. D’une manière générale, on peut dire qu’une gamme serait l’ensemble des intervalles, égaux ou non, qui divisent une octave. Si l’on veut adopter une terminologie rigoureuse, on devrait donc distinguer les gammes , dans lesquelles sont définies les grandeurs des intervalles indépendamment de leur ordre, les modes , dans lesquels on tient compte essentiellement de l’ordre des mêmes intervalles, et les échelles , dans lesquelles les intervalles sont égaux. C’est donc par abus de langage que le seul mot «gamme» est souvent employé pour désigner indifféremment ces divers types de répartitions d’intervalles. Ainsi, dans la musique occidentale, on parle de la gamme naturelle majeure, de la gamme naturelle mineure et de la gamme chromatique. La première est celle qui existe sur les instruments à clavier lorsqu’on se sert des seules touches blanches à partir de la note ut (ou do ): ut , ré , mi , fa , sol , la , si . La deuxième possède deux formes: une forme montante, la , si , ut , ré , mi , fa dièse, sol dièse, et une forme descendante, la , sol bécarre, fa bécarre, mi , ré , ut , si . Enfin, la troisième est tout simplement la suite des demi-tons théoriquement égaux: ut , ut dièse, ré , ré dièse, mi , fa , fa dièse, sol , sol dièse, la , si bémol, si bécarre. Les deux premières sont dites gammes diatoniques ; elles sont constituées par une alternance de tons et de demi-tons. On voit qu’il serait plus logique de parler à propos des «gammes» que nous venons de citer de gamme d’ut dans le mode majeur, de gamme de la dans le mode mineur et d’échelle chromatique. À condition de garder la même répartition des intervalles, toute gamme peut être transposée sans perdre aucune de ses caractéristiques, ce qui veut dire qu’elle peut commencer sur n’importe quelle note. C’est alors la première note qui lui donne son nom. Ainsi, avec les mêmes intervalles que ceux de la gamme d’ut majeur, on peut avoir, par exemple, une gamme dite de ré majeur: ré , mi , fa dièse, sol , la , si , ut dièse. Là encore, pour la rigueur terminologique, il serait préférable de parler du mode d’ut majeur transposé sur ré . Dans leur grande majorité, les gammes, qu’elles soient européennes ou non, sont constituées de sept notes (gammes heptatoniques), mais on rencontre aussi des gammes de cinq sons (pentatoniques) et, bien entendu, la gamme de douze sons (chromatique).
L’idée de la gamme chromatique, formée d’intervalles égaux, est le résultat d’un effort de généralisation provoqué par les nécessités de la polyphonie occidentale et qui se trouve véritablement concrétisé vers la fin du XVIIe siècle. Parmi les préoccupations qui orientèrent la construction des gammes, il y en eut de théoriques (caractérisation de mélodies d’un type donné) et aussi de pratiques, ces dernières étant provoquées par l’existence d’instruments ne pouvant émettre que des sons dont la hauteur était fixée a priori (il s’agit, notamment, des instruments à clavier).
Dans les musiques archaïques ou extra-européennes, essentiellement fondées sur la mélodie, les diverses gammes utilisées peuvent être d’un très grand raffinement, variant parfois de très petits intervalles avec une grande subtilité. Un tel raffinement devient difficile dans le cas de la polyphonie européenne, les rapports régissant la succession des intervalles devant être conciliés avec ceux qui régissent leur superposition. Il est impossible de procéder à un inventaire complet des différentes gammes (européennes, grecques anciennes, indiennes, chinoises, arabes...). On peut dire que chaque gamme correspond à une structure bien définie de la mentalité musicale. Chacune se justifie donc, a posteriori, à partir de la musique qu’elle a permise, de la même manière qu’une langue acquiert ses lettres de noblesse à partir de la littérature qu’elle a suscitée.
La gamme et les modes
Il est vraisemblable que les premières suites de hauteurs de sons (nommées actuellement fréquences ) qui ont été employées par les hommes pour faire de la musique furent suggérées par les harmoniques «naturels». Ces sons harmoniques peuvent être obtenus soit à partir de la vibration en un ou plusieurs fuseaux d’une corde unique, soit à partir de la vibration de l’air dans un tuyau non percé de trous. Les instruments les plus primitifs seraient donc un arc utilisé comme instrument à corde et une flûte formée d’un simple tube. De tels instruments existent encore dans certaines régions d’Afrique, d’Australie ou d’Amérique. Avec eux, les harmoniques naturels sont effectivement privilégiés. Mais on trouve aussi des instruments à sons fixes comme les balafons (xylophones) et même les lithophones. Les enregistrements recueillis permettent d’imaginer une musique qui serait celle des premiers âges de l’humanité. Les gammes qu’on y remarque semblent être le résultat de coutumes autant que de contingences physiques.
Il est toujours vraisemblable (mais seulement vraisemblable) que, à partir de ces données purement physiques, une première divergence se soit produite dans l’évolution. Ou bien on aurait admis la diversité des intervalles résultant des harmoniques naturels, quitte à les expliquer et à les codifier par des méthodes diverses, qui n’excluaient pas le symbolisme et les mythes religieux ou politiques; ou bien, on aurait tenté un effort de rationalisation, au terme duquel on espérait découvrir une génération des intervalles les plus complexes par une combinaison des plus simples. De la première tendance seraient issus les innombrables modes mélodiques (parfois liés à des successions de durées, ou «modes rythmiques») des musiques archaïques ou non européennes. De la seconde on aurait vu naître le «diatonique vulgaire» des Grecs, consolidé par les théories de Pythagore ou d’Aristoxène de Tarente. Mais, comme il est normal, à ce diatonique vulgaire, formé d’une suite de ce que l’on appelle aujourd’hui des tons et des demi-tons, serait venue s’ajouter une multitude de raffinements obtenus par des déplacements subtils (de l’ordre du quart de ton) des différents degrés de ces gammes. Maurice Emmanuel, dans ses ouvrages sur la musique grecque, oppose ainsi une technique qui aurait été celle des philosophes et du peuple à une technique des «professionnels» de la musique. Platon manifeste, d’ailleurs, son mépris pour les subtilités exagérées de ces derniers en les appelant, dans La République , des «tirailleurs de cordes».
À considérer l’ensemble des gammes utilisées, on remarque la présence de deux caractères communs à toutes: un intervalle de base est choisi, qui est l’octave, c’est-à-dire le rapport le plus simple des longueurs de tuyaux ou de cordes vibrantes (1 à 2), et cette octave est divisée en intervalles plus petits d’inégale grandeur. En allant du plus simple au plus compliqué, on trouve donc un très grand nombre de divisions de l’octave, dont la plus élémentaire est formée de deux quartes et d’une seconde majeure (ut-fa-sol-ut ) et dont les plus complexes sont des suites de tons, de demi-tons et de tierces mineures (ou secondes augmentées). La gamme pentatonique, par exemple, que l’imagerie musicale donne comme étant représentative de la musique chinoise, contient des tons et des tierces mineures (ut , ré , mi , sol , la , ut ), et on peut découvrir de multiples modes orientaux possédant les trois intervalles cités plus haut, comme ce mode indien qui, traduit dans notre notation, donnerait approximativement: ut , ré bémol, mi , fa , sol , la bémol, si , ut. Enfin, la plus usuelle des gammes de la musique européenne occidentale à l’époque classique (environ du XVIIe à la fin du XIXe siècle) est une suite de tons et de demi-tons (ut , ré , mi , fa , sol , la , si , ut ).
Cette description des gammes est extrêmement rudimentaire, car on est obligé de se servir d’une notation fondée sur la division de l’octave en douze parties (douze demi-tons), alors que les intervalles constitutifs de l’ensemble des gammes sont infiniment variables et ne peuvent être véritablement représentés qu’à l’aide d’une division de l’échelle sonore en écarts plus petits que le demi-ton. Le choix de cet intervalle, qui serait le plus grand commun diviseur de tous ceux qui ont été utilisés, a donné lieu à des études et à des querelles multiples. Fort heureusement, l’oreille humaine paraît moins exigeante, en général, que l’esprit de rigueur des théoriciens.
Guy d’Arezzo et la gamme
C’est au début du XIe siècle, en recherchant à la fois un système de notation (qui est à l’origine de la portée) et un système de codification des intervalles musicaux, que Guy d’Arezzo aurait imaginé ce qu’on désigne aujourd’hui par le mot «gamme». Partant des «tétracordes» des Grecs, qui s’en servaient pour diviser l’octave en deux parties (par exemple, dans le mode dorien: mi , ré , ut , si /la , sol , fa , mi ) et constatant que, dans certains modes, les tétracordes se chevauchaient (par exemple, dans le mode hypophrygien ou ionien: sol , fa , mi , ré /ré , do , si , la ), Guy d’Arezzo ajouta une note supplémentaire, plus basse que la dernière, et qu’il désigne par la lettre grecque gamma , d’où vint le mot «gamme». Alors que les notes étaient, jusqu’à Guy d’Arezzo, choisies dans les premières lettres de l’alphabet, c’est à lui qu’on attribue le procédé mnémotechnique par lequel on les nomme maintenant dans les pays latins à partir des syllabes initiales d’un hymne à saint Jean-Baptiste:
DIR
\
UT queant laxis
REsonare fibris
MIra gestorum
FAmuli tuorum
SOLve polluti
LAbii reatum
Sancte Ioannes./DIR
Dans les pays anglo-saxons ayant conservé la notation des notes de la gamme par des lettres, la correspondance, de nos jours, s’établit comme suit:
DIR
\
La gamme dite de Pythagore
Les conceptions pythagoriciennes sont, essentiellement, de nature arithmétique. La perfection des rapports de consonance des sons entre eux serait liée à la simplicité des rapports numériques des longueurs de corde vibrante. Une corde de longueur l donnant une note dont la hauteur est prise comme référence, les rapports les plus simples sont donnés par la corde de longueur 2 l (octave inférieure) et 3 l (douzième inférieure). Le rapport 2 est considéré comme «infécond», puisque n’étant capable que de reproduire toujours la même note à des octaves différentes. Il n’est donc utilisé que pour ramener les notes à l’intérieur d’une même octave, en divisant par deux les longueurs de corde. En revanche, le rapport 3, étant à l’origine de ce qu’on appelle maintenant le cycle des quintes, permet d’obtenir toutes les notes de la gamme soit, par quintes successives: si , mi , la , ré , sol , ut , fa. Ce qui, converti dans une même octave (c’est-à-dire entre les longueurs de corde l et 2 l ), donne les longueurs de corde suivantes, représentatives du mode dorien:
DIR
\
1 9/8 81/64 4/3 3/2 27/16 243/128 2
On remarque que les intervalles de ce mode, pris en descendant, sont les mêmes que ceux de la gamme diatonique majeure pris en montant, d’où cette forme moderne, connue aussi sous le nom de gamme de Pythagore, dans laquelle les nombres désignent, cette fois-ci, des rapports de fréquence:
DIR
\
1 9/8 81/64 4/3 3/2 27/16 243/128 2
Cette inversion du sens des intervalles, suivant que l’on considère des fréquences ou des longueurs de corde, est sans doute à l’origine de la légende selon laquelle les modes grecs étaient énoncés sous la forme descendante.
Si l’on mesure les intervalles séparant deux notes voisines, on constate qu’il n’en existe que deux: le ton (rapport 9/8) et le demi-ton (rapport 256/243).
Les systèmes d’Aristoxène et de Zarlino
Opposés aux pythagoriciens en ce qu’ils n’attribuaient aucune valeur souveraine à la perfection des nombres, les disciples d’Aristoxène de Tarente (IVe siècle av. J.-C.) étaient cependant attachés à la théorie des divisions de la corde vibrante dans des rapports «harmoniques»; ils attribuaient à cette théorie une valeur à la fois physique et esthétique. Il semble que deux divisions différentes des longueurs de corde aient été connues d’eux. La première correspond à ce que, aujourd’hui, l’on sait être la suite des «harmoniques naturels». C’est la série:
DIR
\
1 1/2 1/3 1/4 1/5 1/6 1/7 1/8 etc.
correspondant aux fréquences f , 2 f , 3 f , 4 f , 5 f , 6 f , 7 f , 8 f , etc., et dont les cinq premières constituent l’accord parfait majeur (ut-mi-sol ). La seconde utilisait une division arbitraire en six parties égales:
DIR
\
1(6/6) 5/6 4/6 3/6 2/6 1/6 0
correspondant aux fréquences f , 6 f /5, 3 f /2, 2 f , 3 f , 6 f , et dont est tiré l’accord parfait mineur (ut-mi bémol-sol ).
La première division est dite division harmonique , la seconde division arithmétique. Elles sont apparemment inconciliables. C’est pourtant en essayant de les concilier que Gioseffo Zarlino, au XVIe siècle, inventa la théorie du «dualisme harmonique», d’où découle à la fois une gamme diatonique majeure et une gamme diatonique mineure. Ces gammes reçurent au XVIIIe siècle une justification théorique due à Joseph Sauveur, puis à Rameau et à d’Alembert.
La gamme des physiciens, dite aussi de Zarlino
Si l’on recherche un compromis heureux entre la gamme de Pythagore, la suite des harmoniques naturels et la division arithmétique des cordes vibrantes (cette dernière donnant la tierce mineure de rapport 6/5), on trouve la gamme des physiciens, appelée aussi gamme de Zarlino. Elle est fondée sur la superposition de trois accords parfaits majeurs: fa-la-ut , ut-mi-sol et sol-si-ré. Elle se réfère donc à la fois au rapport 3/2 (quinte pythagoricienne), au rapport 5/4 (tierce harmonique) et au rapport 2 (octave). On y remarque la série de fréquences suivante:
DIR
\
1 9/8 5/4 4/3 3/2 5/3 15/8 2
et les intervalles la-ut et mi-sol sont dans le rapport 6/5, soit celui de la tierce mineure de la division arithmétique. Malheureusement, cette gamme possède les trois inconvénients suivants:
– Si l’on compare les intervalles des diverses notes voisines, on constate qu’il en existe trois (alors que la gamme de Pythagore n’en avait que deux): un demi-ton égal au rapport 16/15 entre mi-fa et si-ut et deux tons inégaux valant respectivement 9/8 (ut-ré ) et 10/9 (ré-mi ). La différence entre ces deux sortes de tons est égale à 9/8: 10/9 = 81/80; on l’appelle comma. Cette différence, quoique très petite, est perceptible à l’oreille.
– L’intervalle ré-la , qui devrait être égal à une quinte pythagoricienne, c’est-à-dire à 3/2, est plus petit puisqu’il équivaut à 40/27; c’est une quinte diminuée d’un comma.
– Ce même intervalle ré-la reste difficile à transposer, étant donné l’existence du comma. La gamme qui serait construite à partir de ré , par exemple (gamme de ré majeur), aurait une quinte fausse si le la n’était pas relevé d’un comma. Ce comma étant approximativement égal à un neuvième de ton, il en résulte que, dans les transpositions, les notes altérées sont placées à une distance inégale de celles qui les précèdent et de celles qui les suivent. Ainsi, le fa dièse doit être plus près du sol que du fa.
En revanche, l’un des grands avantages de la gamme des physiciens est que chacun de ses sons peut être considéré comme obtenu par génération d’harmoniques naturels. Helmholtz a émis, dans les années 1850, la théorie selon laquelle cette circonstance rendrait compte de l’agrément particulier de cette gamme.
Werckmeister et la gamme tempérée
Les divers inconvénients que présentent les gammes de Pythagore et de Zarlino ont pour origine le problème suivant: comment faire coexister, dans un même système, des quintes justes et des octaves justes? Or, un raisonnement élémentaire permet de voir que ce problème n’a pas de solution. En effet, les quintes sont le résultat d’une itération du rapport 3 et les octaves celui d’une itération du rapport 2. Il faudrait donc découvrir une puissance de 3 qui soit égale à une puissance de 2. Comme les puissances de 3 sont toujours des nombres impairs (se terminant par 1, 3, 7 ou 9) et que les puissances de 2 sont toujours des nombres pairs, il n’existe pas de solution. Cependant, à la fin du XVIIe siècle, Andreas Werckmeister (1645-1706) parvint à trouver un compromis qui, une fois de plus, résultait d’un effort de généralisation et que, depuis lors, on utilise sous le nom de gamme tempérée.
Dans le système pythagoricien de génération des intervalles par quintes, on s’aperçoit que, à partir de la douzième quinte, on retrouve, à peu près, la septième octave de la note de départ:
DIR
\
1 3/2 9/4 27/8 81/16 243/32 729/64
2 187/128 6 561/256 19 683/512
ut 戀凉 sol 戀凉 ré 戀凉
59 049/1 024 177 147/2 048 531 441/4 096
la 戀凉 mi 戀凉 si 戀凉 (ou ut )/DIR
étant la suite des quintes, et la suite des puissances de 2:
DIR
\
1 2 4 8 16 32 64 128
étant celle des octaves. On voit que le rapport 531 441/4 096 = 129,746 est légèrement plus grand que le rapport 128. C’est donc par une approximation exigée par la pratique que l’on identifie le si dièse à l’ut ; la différence qui les sépare est appelée comma pythagoricien. L’idée de Werckmeister est alors d’une géniale simplicité: il décide de répartir cette petite différence de telle sorte que, chaque quinte étant raccourcie de 1/12 de comma pythagoricien, la note engendrée par la douzième quinte corresponde à celle que donne la septième octave. Autrement dit, il pose l’équation: douze quintes = sept octaves. Il résulte de cette égalité que, une fois ramenées à l’intérieur d’une même octave par un nombre convenable de divisions par 2, les douze notes de la série des quintes divisent cette octave en douze parties égales ou douze demi-tons tempérés. Un autre mérite de Werckmeister est d’avoir aussi établi une méthode pour accorder les instruments selon ce «tempérament». L’inconvénient de la gamme tempérée est de donner des intervalles qui, à l’exclusion de l’octave, sont tous «faux» par rapport aux résonances naturelles (les quintes étant trop petites). Mais l’avantage énorme du système est de permettre toutes les transpositions et d’ouvrir aux musiciens la possibilité d’écrire dans toutes les tonalités en utilisant les instruments à clavier à douze touches par octave.
Divisions de l’octave en parties égales
Ni tous les musiciens ni tous les théoriciens ne se montrèrent et ne se montrent encore satisfaits d’un système dans lequel toutes les divisions de l’octave sont égales. Jusqu’à la fin du XVIIIe siècle, divers tempéraments furent employés (on appelait tempérament tout système dans lequel on sauvegardait la justesse d’un certain nombre de quintes et de tierces tout en en sacrifiant quelques-unes). En revenant à la règle générale par laquelle on s’efforce d’obtenir simultanément des octaves et des quintes justes, on cherchera donc quelles sont les puissances de 3/2 qui sont les plus voisines d’une puissance de 2. Werckmeister avait déjà remarqué que (3/2)12 est voisin de 27; mais d’autres divisions de l’octave sont possibles; on peut notamment citer les suivantes: 31, puisque (3/2)31 est voisin de 218; 41, puisque (3/2)41 est voisin de 224; et 53, puisque (3/2)53 est très proche de 231. Dans les années 1950, Adriaan Fokker construisit à Haarlem un orgue à trente et un degrés par octave. Dans la seconde moitié du XIXe siècle, Pál Janko, à Prague, réalisa des pianos à quarante et un degrés par octave dont le clavier se composait de six rangées de touches superposées! Mais, sans qu’on ait jamais essayé de construire un instrument à cinquante-trois touches par octave (nous n’avons que dix doigts...), il semble que ce soit la division de l’octave en cinquante-trois parties égales qui se soit montrée la plus intéressante. C’est elle, en effet, qui génère un tempérament dans lequel on trouve deux demi-tons, l’un dit chromatique et l’autre diatonique , qui valent respectivement 5 et 4 cinquante-troisièmes d’octave. Par abus de langage, le cinquante-troisième d’octave est ici appelé aussi comma . On a alors la gamme suivante (l’intervalle entre deux notes étant donné en cinquante-troisièmes d’octave):
DIR
\
Cette gamme présente deux avantages; le premier est qu’elle permet aux instruments à clavier de jouer dans toutes les tonalités, chacune d’elles gardant une couleur particulière; le second est que l’intervalle de quinte y est pratiquement juste: 1,499 94 au lieu de 1,5. Il est vraisemblable que ce tempérament ait été celui de Jean-Sébastien Bach pour le Wohltemperierte Klavier plutôt que le tempérament rigoureusement égal.
Parmi les gammes non européennes, il faut citer les modes indiens, dans lesquels existe une division de l’octave en vingt-deux parties, dites çrutis . Mais s’il y a bien vingt-deux çrutis par octave, il y a trois çrutis différents; l’octave n’est donc pas divisée en vingt-deux parties égales. Toutefois, les mesures effectuées à partir d’enregistrements montrent que, dans la pratique, les musiciens indiens exécutent les différents çrutis d’une manière assez approximative.
Il est remarquable de constater que, pour obtenir une division de l’octave en parties égales, il suffit de posséder un nombre tel que sa multiplication par lui-même autant de fois qu’il y a de parties de l’octave considérée soit égale à 2. La fréquence de chaque note, multipliée par ce nombre, donne la fréquence de la note immédiatement supérieure. Ce nombre représente donc l’intervalle de base. Il est égal à 12 連2 dans le système tempéré occidental, à 31 連2 dans celui de Fokker, à 41 連2 dans celui de Janko et à 53 連2 dans le système au cinquante-troisième d’octave, dont la théorie avait été exposée au XVIIe siècle par William Holder et Nicolaus Mercator.
Le fait que, pour passer d’une note à une autre, il soit nécessaire de multiplier sa fréquence par un nombre donné et l’habitude qu’ont les musiciens d’additionner les intervalles ont conduit le mathématicien Euler (1707-1783) à proposer les logarithmes comme une méthode de mesure commode des intervalles musicaux. D’après Euler, le système tempéré serait donc celui dont les intervalles (mesurés en demi-tons) sont désignés par la suite des nombres entiers dans les logarithmes à base 12 連2. Mais le nombre 12 連2 n’est pas facilement maniable. C’est pourquoi l’acousticien Félix Savart proposa, au début du XIXe siècle, un intervalle pouvant représenter le plus petit qui soit perceptible par l’oreille humaine dans les conditions habituelles d’écoute (soit ce fameux «plus grand commun diviseur» de tous les intervalles utilisables); cet intervalle se référait à l’octave, c’est-à-dire au rapport 2, et Savart utilisait des logarithmes de base «pratique», soit la base 10. En prenant comme intervalle de référence log10 2 = 0,301 03, on avait un intervalle trop grand. Savart proposa donc le millième de cet intervalle, soit 1 000 log10 2 = 301,03. Il y a donc 301 savarts (puisque cet intervalle porte le nom de son inventeur) dans une octave, et l’intervalle qui sépare deux notes se mesure, à partir de leurs fréquences respectives f 1 et f 2 (f 2 supérieur à f 1), par la formule:

Vers la plus grande généralisation possible
Il ressort de tout ce qui précède que l’évolution des modes et des gammes se traduit par un effort constant pour donner à l’ensemble des fréquences audibles une sorte de statut qui permette de choisir, l’une étant prise comme fréquence de base, celles qui serviront ensuite à faire véritablement de la musique. De ce point de vue, le système tempéré occidental est un immense succès puisqu’on lui doit, depuis Bach, une grande quantité de chefs-d’œuvre. Il est possible, toutefois, que ce système ne dure pas plus que ceux qui l’ont précédé. Les moyens électroniques, notamment, permettent d’imaginer d’autres divisions de l’espace sonore. Ainsi, suivant en cela l’exemple d’Euler, on pourrait choisir pour logarithmes, non plus la base 12 連2, mais une base qui serait la plus «générale» possible, soit n 連p . De cette façon, p représenterait l’intervalle destiné à être divisé en n parties égales. Cette proposition n’est pas une vue de l’esprit. Dans son Étude I de musique électronique, Karlheinz Stockhausen a choisi la base 28 連5, étendant par là le tempérament à la division en vingt-huit parties égales de l’intervalle existant entre un son fondamental et son cinquième harmonique.
Partant de la notion de mode , c’est-à-dire de la division de l’octave en parties inégales, la gamme tend, de nos jours, à rejoindre la notion d’échelle (dont la gamme chromatique est la forme la plus usuelle), qui serait une division en parties égales de l’espace sonore.
Quoique employée sans discussion par presque tous les musiciens, la gamme tempérée n’est pas encore, pour autant, admise par tous les théoriciens. On peut encore discuter longtemps des mérites respectifs des différentes gammes qui ont été présentées ici, et si certains esprits éminents prônent ceux de la gamme de Pythagore, d’autres recherchent de nouveaux compromis (comme la gamme à trente et un degrés). On a cru constater, par exemple, qu’un violoniste non accompagné par le piano (le piano étant l’instrument tempéré par excellence) joue dans la gamme de Pythagore. Il y aurait alors deux explications à ce phénomène: ou bien la gamme de Pythagore serait une gamme «instinctive» et, par conséquent, la meilleure de toutes, ou bien, le violon étant un instrument accordé par quintes, il serait tout à fait normal que les violonistes jouent naturellement dans une gamme qui est obtenue par une juxtaposition de quintes. On est, en réalité, dans un domaine où, plus qu’en tout autre, le mouvement se prouve en marchant. La gamme de Pythagore est la meilleure des gammes puisque Bach a composé les Suites pour violon seul , mais la gamme tempérée est aussi la meilleure puisque le Clavier bien tempéré existe également.
Depuis le début du XXe siècle, de nombreux compositeurs utilisent des intervalles plus petits que le demi-ton. Les pionniers en la matière furent Julián Carillo, Aloys Haba et Ivan Vychnegradsky. Avec les musiques dites concrètes, électroniques ou électro-acoustiques, les diverses théories sur la constitution des gammes se trouvent naturellement négligées.
En revanche, les historiens et musicologues se livrent encore parfois quelques combats au sujet de ce que l’on doit penser des théories anciennes et, surtout, de la manière dont elles étaient mises en pratique. De même, après plusieurs siècles de considérations parfois hasardeuses, l’ethnomusicologie s’étant enrichie de cet instrument de travail efficace qu’est la technique de l’enregistrement sonore, fit des progrès considérables et nous avons de nouvelles lumières sur les diverses gammes folkloriques ou non européennes.
En ce qui concerne le tempérament égal, toujours sujet à discussion, une thèse séduisante de Serge Cordier propose, pour l’accord des instruments à clavier, une division de la quinte en sept parties égales plutôt que celle de l’octave en douze parties égales. Il semble que l’acoustique physiologique lui donne raison, l’oreille étant plus sensible à la justesse de la quinte et acceptant volontiers des octaves légèrement trop grandes.
gamme [ gam ] n. f.
1 ♦ Mus. Échelle de sons établie selon une répartition conventionnelle. Gamme diatonique naturelle, tempérée. Gamme chromatique. Note de la gamme. ⇒ degré.
♢ Cour. Suite des sept notes comprises dans l'intervalle d'une octave. Gamme ascendante, descendante. Monter, descendre la gamme. La gamme de do majeur, de la mineur. — Faire ses (des) gammes au piano. Fig. Faire ses gammes : s'exercer.
2 ♦ Série, succession (de teintes, de couleurs) en gradation naturelle. Une gamme de nuances. « une gamme qui va du blanc au brun en passant par les ocres » (Malraux).
3 ♦ (1840) Fig. Série continue où tous les degrés, toutes les espèces sont représentés. Toute la gamme des sentiments, des sensations. Proposer une gamme de prix. ⇒ éventail. « La charité, l'indulgence, la mansuétude, voilà toute une gamme de vertus » (Duhamel). — Série de produits comparables, appartenant à une même catégorie, classés selon leur utilisation, leur prix, etc. Une gamme assez large de services. Un nouveau produit qui vient enrichir une gamme.
♢ Loc. HAUT DE GAMME; BAS DE GAMME : l'ensemble des produits les plus chers, les moins chers dans une telle série. Choisir un produit de qualité dans le bas de gamme. Appos. Téléviseurs haut de gamme, bas de gamme. — Par ext. Une émission bas de gamme. — REM. On trouve aussi milieu de gamme.
♢ Catégorie de produits alimentaires classés selon leur mode de conservation (frais, surgelés ou conservés). Quatrième gamme : produits frais, crus, prêts à l'emploi. Cinquième gamme : produits précuits ou cuits conservés sous vide.
● gamme nom féminin (latin médiéval gamma, du grec gamma) Fragment de l'échelle musicale qui se caractérise par sa structure. Série de choses de même nature, mais présentant divers aspects, divers degrés, diverses nuances : Une gamme de beiges, du plus clair au plus foncé. Série d'objets de même fonction allant du moins cher au plus cher, de la qualité la plus médiocre à la meilleure qualité, du moins perfectionné au plus perfectionné, etc. : Une gamme de téléviseurs. Imprimerie Ensemble des épreuves de contrôle d'une sélection pour l'impression en quadrichromie. Télécommunications Bande de fréquences à l'intérieur de laquelle les ondes électromagnétiques ont des propriétés peu différentes, ou à l'intérieur de laquelle un appareil peut fonctionner ou être réglé. ● gamme (expressions) nom féminin (latin médiéval gamma, du grec gamma) Faire des gammes, exécuter sur un instrument ou avec la voix des exercices musicaux en forme de gammes ; s'initier à une nouvelle technique par des exercices suivis. Le haut, le bas de (la) gamme, les articles qui se situent au niveau supérieur, ou inférieur, du point de vue du prix, de la qualité, du perfectionnement (peut s'employer en apposition : Un four électrique haut de gamme). Gamme de gris, bande constituée de plages gris neutre de différentes intensités, que l'on place avec le document pour le contrôle de l'équilibre des valeurs en photogravure. Gamme d'opérations, document donnant le détail des opérations d'un travail à effectuer avec, pour chacune, le personnel, les machines, les dessins et l'outillage nécessaires, éventuellement le temps alloué. Gamme d'ordinateurs, famille d'ordinateurs d'un même constructeur présentant des caractéristiques similaires de jeux d'instructions et de systèmes d'exploitation. ● gamme (synonymes) nom féminin (latin médiéval gamma, du grec gamma) Série de choses de même nature, mais présentant divers aspects...
Synonymes :
- éventail
- panoplie
Série d'objets de même fonction allant du moins cher au...
Synonymes :
- ligne
gamme
n. f.
d1./d MUS Suite ascendante ou descendante de notes conjointes, disposées selon les lois de la tonalité sur l'étendue d'une octave. (La musique occidentale connaît les gammes diatoniques et chromatiques. Les gammes diatoniques se divisent en deux séries: majeures et mineures, dont le septième degré est augmenté d'un demi-ton.)
d2./d Fig. Ensemble de couleurs, d'états, d'objets, etc., qui s'ordonnent comme une gradation. La gamme des bleus. La gamme complète des voitures produites par une firme.
d3./d Toute la gamme des: l'ensemble complet des. Utiliser toute la gamme des antibiotiques. Passer par toute la gamme des sentiments.
⇒GAMME, subst. fém.
A. — MUS. Suite des notes d'un système musical donné (mode), comprises dans les limites d'une octave, séparées par des intervalles déterminés et disposées dans l'ordre des fréquences croissantes ou décroissantes. Gamme ascendante, montante, descendante; les notes de la gamme; chanter une gamme; monter la gamme; égrener des gammes; faire des gammes et des exercices. Ut, ré, mi, fa, sol. Ces cinq tons sont la gamme naturelle de la voix, et donnent une phrase musicale pleine et agréable (CHATEAUBR., Génie, t. 2, 1803, p. 4). Mlle Aglaé fut priée de chanter, elle se mit au piano, enfila des gammes, hennit, piaffa, pompa et brossa le clavier (FLAUB., Éduc. sent., 1845, p. 42). D'une croisée ouverte au premier étage, une gamme en mineur, qui trébuche sur les touches d'un clavier poussif, égrène jusqu'à la rue ses notes hésitantes (MARTIN DU G., Vieille Fr., 1933, p. 1072) :
• 1. ... toute gamme, tempérée ou non, de Zarlin, de Pythagore ou de Bach, est fondée, à une approximation près, sur la quinte et l'octave, c'est-à-dire les rapports les plus simples 2 sur 1 et 3 sur 2...
SCHAEFFER, Rech. mus. concr., 1952, p. 126.
♦ Gamme chromatique. Gamme qui procède par demi-tons successifs, soit en montant, soit en descendant. Il précipite d'un bout à l'autre du clavier poussif une vertigineuse gamme chromatique; la voix lointaine, sonnaillante du vieux piano s'essouffle à suivre les doigts (MARTIN DU G., Devenir, 1909, p. 31).
♦ Gamme diatonique. Gamme composée d'une suite de sept notes dont tous les intervalles sont des tons ou des demi-tons d'égale grandeur. Gamme diatonique majeure, gamme diatonique mineure. La gamme diatonique et les bons vieux accords classiques, avec certains développements modernes bien entendu, ne seraient-ils pas la base de l'écriture chorale? (POTIRON, Mus. église, 1945, p. 40).
♦ Gamme défective. Gamme ayant moins de sept notes (d'apr. Mus. 1976). Le rythme est souverain dans la musique de Bartok, et l'emploi d'une gamme défective pentatonique assez fréquent (DUMESNIL, Hist. théâtre lyr., 1953, p. 215).
♦ Gammes relatives. Gammes de même armature, mais dont l'une est majeure, l'autre mineure. Nous sommes donc autorisés à considérer cette gamme descendante du mi au mi, comme la véritable relative de celle d'Ut majeur (D'INDY, Compos. mus., t. 1, 1897-1900, p. 102). Les sons primes de deux gammes relatives de mode différent (...) sont placés symétriquement (D'INDY, Compos. mus., t. 1, 1897-1900p. 105).
— Loc. fig., fam.
♦ Changer de gamme. Changer de ton, de manière d'être ou de faire. Elle a toujours l'air de me mépriser, et, pourtant, si elle a manqué à la vertu, elle devrait bien changer de gamme (DURANTY, Malh. H. Gérard, 1860, p. 221). Quand il verra le succès de ton livre et les journaux tout remplis de toi, il changera joliment de gamme (A. DAUDET, Pt chose, 1868, p. 252).
♦ Chanter une (sa) gamme (à qqn) (vx). Énumérer tous les griefs que l'on a contre quelqu'un, faire des reproches à quelqu'un. Il [le Secrétaire général] me chanterait une gamme d'enfer s'il savait qu'elle [une lettre] n'est pas à son adresse (BALZAC, Employés, 1837, p. 223).
Rem. 1. Emploi de gamme dans le sens de « série de reproches, de griefs » (avec l'idée de quelque chose d'habituel, de répétitif). Il vous semble mal. Vous n'êtes qu'un être insupportable; je ne puis pas vous souffrir. J'étais fait à cette gamme; je ne m'en émus pas (REYBAUD, J. Paturot, 1842, p. 23). 2. Pop. Faire chanter sa gamme (à qqn), faire monter la gamme. Donner une correction (en faisant crier). Tu rentres en retard, tu vas voir si le père va te faire chanter; il te fera monter la gamme (BRUANT 1901, p. 10).
♦ Être au bout de sa gamme. N'avoir plus rien à dire. J'allais le prendre [le Chouan] pour un imbécile. Lui et moi nous aurions fait la paire. J'étais au bout de ma gamme (BALZAC, Chouans, 1829, p. 31).
♦ Faire des (ses) gammes. Faire des exercices pour acquérir une technique, une faculté. J'admire la mémoire du mathématicien, et même je l'envie; mais c'est que je n'ai point fait mes gammes comme il a fait (ALAIN, Propos, 1921, p. 205).
B. — P. anal. Série de couleurs, de tons gradués. Gamme de couleurs, de nuances; gamme de gris, de verts; gamme de tons orangés. Corot (...) sait être coloriste avec une gamme de tons peu variée (BAUDEL., Salon, 1845, p. 61). À mesure que la journée avance, elle [la mer] change de couleur, et monte la gamme des bleus... Vers midi, elle est saphiréenne, mais s'arrête au vert (BARB. D'AUREV., Memor. 4, 1858, p. 97) :
• 2. Une exposition de soies, de satins et de velours, y épanouissait [derrière la vitrine], dans une gamme souple et vibrante, les tons les plus délicats des fleurs : au sommet, les velours, d'un noir profond, d'un blanc de lait caillé; plus bas, les satins, les roses, les bleus, aux cassures vives, se décolorant en pâleurs d'une tendresse infinie; plus bas encore, les soies, toute l'écharpe de l'arc-en-ciel...
ZOLA, Bonh. dames, 1883, p. 391.
C. — P. ext. Série quelconque dont tous les éléments constituent une gradation continue.
1. [Éléments concr.] Une gamme de produits. V. impedimenta ex. Une gamme de formats d'une grande variété de dimensions et de présentation (Civilis. écr., 1939, p. 6-8). On voyait sur la scène un homme attaché et bâillonné sur qui un fou armé d'aiguilles et d'un scalpel allait essayer toute une gamme de tortures savantes (GREEN, Journal, 1941, p. 51). La réalisation d'une gamme d'engins de puissance comprise entre le vingtième et vingt fois celle de l'arme utilisée en 1945 (GOLDSCHMIDT, Avent. atom., 1962, p. 93).
Rem. Emploi très vivant actuellement dans le domaine du commerce et des services. Gamme de spots publicitaires; gamme de services; gamme de voitures; gamme hôtelière (d'apr. GILB. 1971). V. haut de gamme.
2. [Éléments abstr. : affects, idées, etc.] Gamme des passions, des sentiments. Mademoiselle Mars donne au rôle un développement immense. Elle y parcourt en quelques instans toute la gamme de son talent, du gracieux au sublime, du sublime au pathétique le plus déchirant (HUGO, Hernani, 1830, p. 154). La charité, l'indulgence, la mansuétude, voilà toute une gamme de vertus qu'il me faut acquérir (DUHAMEL, Journ. Salav., 1927, p. 17) :
• 3. ... de proche en proche, mais encore, dans une même région de l'organisme, elle [la mort] se produit par degrés, par nuances; entre la disparition des premières et des dernières propriétés vitales, il y a toute une gamme d'intermédiaires. Tant que la matière organisée n'a pas subi la putréfaction définitive, on hésitera à affirmer qu'il n'y subsiste pas un ultime reliquat de vie.
J. ROSTAND, La Vie et ses probl., 1939, p. 108.
D. — Emplois spéc.
1. MÉCAN. INDUSTR. Suite logique, s'échelonnant dans un temps donné, d'opérations à effectuer sur une pièce pour obtenir un produit fini. Gamme d'usinage, de montage ou de démontage (d'apr. BOISSIER 1975).
2. TÉLÉCOMM. Ensemble des longueurs d'ondes comprises entre deux fréquences données. [La] gamme dite « marine » [...] comprend toutes les fréquences situées entre 1600 et 3260 kHz, soit environ de 92 à 185 m. Elle est donc située entre la fin de la gamme ondes courtes et le début de la gamme ondes moyennes (L'Autojournal, 17 juill. 69 ds GILB. 1971).
Prononc. et Orth. [gam]. Ds Ac. 1718-1932. Étymol. et Hist. Ca 1155 mus. (Thèbes, éd. G. Raynaud de Lage, 4994 : par la gamme Chante Musique); p. anal. 1830 la gamme de son talent (HUGO, loc. cit.); 1837 la gamme des sensations joyeuses (BALZAC, C. Birotteau, p. 326); en partic. 1845 peint. une gamme de tons très grise (BAUDEL., Salon, p. 43). Empr. au lat. médiév. gamma (< gr. 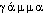 , nom de la 3e lettre de l'alphabet gr.) utilisé par Gui d'Arezzo († 1050) pour désigner la 1re note de la gamme, puis la gamme elle-même : cf. 1033, Chron. Turon. ap. Marten, t. 5, Ampl. Collect. col. 999 ds DU CANGE, s.v. Gama : Clarebat in Italia Guido Aretinus mirabilis musicus, qui Gammam et regulas cantus composuit, et sex vocibus, quas solas musica recipit, nomina imposuit; d'Arezzo désigna les six notes de ut à la d'apr. les six syllabes de la 1re strophe de l'hymne à St-Jean-Baptiste de Jean Diacre; cette première note ut, était aussi appelée gamm(a)ut : 1223-27 (G. DE COINCI, De Ste Leocade, 784 ds T.-L.), encore ds Trév. 1771; G. DE COINCI, op. cit., notes p. 111; Z. rom. Philol. t. 26, pp. 720-722. Fréq. abs. littér. : 382. Fréq. rel. littér. : XIXe s. : a) 214, b) 563; XXe s. : a) 664, b) 740.
, nom de la 3e lettre de l'alphabet gr.) utilisé par Gui d'Arezzo († 1050) pour désigner la 1re note de la gamme, puis la gamme elle-même : cf. 1033, Chron. Turon. ap. Marten, t. 5, Ampl. Collect. col. 999 ds DU CANGE, s.v. Gama : Clarebat in Italia Guido Aretinus mirabilis musicus, qui Gammam et regulas cantus composuit, et sex vocibus, quas solas musica recipit, nomina imposuit; d'Arezzo désigna les six notes de ut à la d'apr. les six syllabes de la 1re strophe de l'hymne à St-Jean-Baptiste de Jean Diacre; cette première note ut, était aussi appelée gamm(a)ut : 1223-27 (G. DE COINCI, De Ste Leocade, 784 ds T.-L.), encore ds Trév. 1771; G. DE COINCI, op. cit., notes p. 111; Z. rom. Philol. t. 26, pp. 720-722. Fréq. abs. littér. : 382. Fréq. rel. littér. : XIXe s. : a) 214, b) 563; XXe s. : a) 664, b) 740.
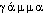 , nom de la 3e lettre de l'alphabet gr.) utilisé par Gui d'Arezzo († 1050) pour désigner la 1re note de la gamme, puis la gamme elle-même : cf. 1033, Chron. Turon. ap. Marten, t. 5, Ampl. Collect. col. 999 ds DU CANGE, s.v. Gama : Clarebat in Italia Guido Aretinus mirabilis musicus, qui Gammam et regulas cantus composuit, et sex vocibus, quas solas musica recipit, nomina imposuit; d'Arezzo désigna les six notes de ut à la d'apr. les six syllabes de la 1re strophe de l'hymne à St-Jean-Baptiste de Jean Diacre; cette première note ut, était aussi appelée gamm(a)ut : 1223-27 (G. DE COINCI, De Ste Leocade, 784 ds T.-L.), encore ds Trév. 1771; G. DE COINCI, op. cit., notes p. 111; Z. rom. Philol. t. 26, pp. 720-722. Fréq. abs. littér. : 382. Fréq. rel. littér. : XIXe s. : a) 214, b) 563; XXe s. : a) 664, b) 740.
, nom de la 3e lettre de l'alphabet gr.) utilisé par Gui d'Arezzo († 1050) pour désigner la 1re note de la gamme, puis la gamme elle-même : cf. 1033, Chron. Turon. ap. Marten, t. 5, Ampl. Collect. col. 999 ds DU CANGE, s.v. Gama : Clarebat in Italia Guido Aretinus mirabilis musicus, qui Gammam et regulas cantus composuit, et sex vocibus, quas solas musica recipit, nomina imposuit; d'Arezzo désigna les six notes de ut à la d'apr. les six syllabes de la 1re strophe de l'hymne à St-Jean-Baptiste de Jean Diacre; cette première note ut, était aussi appelée gamm(a)ut : 1223-27 (G. DE COINCI, De Ste Leocade, 784 ds T.-L.), encore ds Trév. 1771; G. DE COINCI, op. cit., notes p. 111; Z. rom. Philol. t. 26, pp. 720-722. Fréq. abs. littér. : 382. Fréq. rel. littér. : XIXe s. : a) 214, b) 563; XXe s. : a) 664, b) 740.
gamme [gam] n. f.
ÉTYM. Mil. XIIe, game; de la lettre grecque gamma, employée par Gui d'Arezzo pour désigner, concurremment avec ut, la première note de la gamme, puis la gamme elle-même, appelée longtemps aussi gamma-ut et gamm'ut (encore au XVIIIe dans le Dictionnaire de Trévoux).
❖
1 (Mil. XVIe). Cour. Dans un système musical donné (⇒ Mode), Suite des hauteurs par mouvement conjoint (ascendant ou descendant), comprises dans l'intervalle d'une octave. ⇒ Échelle (cit. 15; et → aussi Chant, cit. 10). || Gamme ascendante, descendante. || Gamme de cinq sons (pentatonique), de six, de sept sons. || Gammes de Pythagore, d'Euler, basées sur des rapports numériques. || Gamme naturelle ou diatonique majeure, de Zarlin, « construite sur le principe de l'affinité des sons » (R. Husson). — Gammes utilisées dans l'Occident actuel : gamme tempérée, où l'octave est divisée en douze demi-tons égaux. ⇒ Chromatique (cit. 1 et supra). || Gamme diatonique, formée de tons et de demi-tons. || Gamme majeure, mineure, caractéristiques des modes majeur et mineur. ⇒ Mode. || Gammes relatives : gamme majeure et sa relative mineure. ⇒ Ton, tonalité. || Gammes enharmoniques.
1 On appelle gamme un mode de division de l'échelle continue des sons en degrés discontinus, exigé par les besoins pratiques de l'art musical. L'extrême parenté des octaves conduit à ne se préoccuper que de la subdivision de l'intervalle d'octave.
R. Husson, in Encycl. franç. (De Monzie), XVI, 34-8.
2 Ce n'est plus qu'une masse de vibrations sonores qui se dégage sans cesse des innombrables clochers (…) Cependant cette mer d'harmonie n'est pas un chaos (…) Vous y voyez serpenter à part chaque groupe de notes qui s'échappe des sonneries (…) vous y voyez sauter les octaves d'un clocher à l'autre (…) vous admirez au milieu d'elles la riche gamme qui descend et remonte sans cesse les sept cloches de Saint-Eustache (…)
Hugo, Notre-Dame de Paris, III, II.
2.1 Lorsque Passepartout apprit ce que coûterait cette dernière traversée, il poussa un de ces « oh ! » prolongés, qui parcourent tous les intervalles de la gamme chromatique descendante !
J. Verne, le Tour du Monde en 80 jours, p. 294 (1873).
3 La voix de Me Pelletot monta en prononçant la dernière phrase, comme monte la gamme des dernières gouttes d'eau qui remplissent un vase.
A. Maurois, Bernard Quesnay, I.
♦ (Fin XIXe, au propre et au figuré). || Faire, ânonner (cit. 4) ses gammes au piano (→ Claustral, cit.). || Chanter la gamme pour exercer sa voix.
4 (…) sûr de n'être entendu de personne, il faisait sur des « O », des « A », des « I », roulés, des gammes lentes, passant de l'aigu au plus grave et du flûté en voix de tête au râle funèbre.
H. Bosco, Antonin, p. 74.
♦ Par métaphore. Exercice. || Ces premiers poèmes n'étaient que des gammes.
5 Mais ce ne sont là qu'essais et gammes, et la nouvelle belle Hélène avait été déjà deux ou trois fois fiancée (…)
Émile Henriot, Portraits de femmes, p. 421.
♦ ☑ Loc. (1648). Vx. Chanter à qqn sa gamme, énumérer les reproches qu'on lui fait. — ☑ (1665). Changer de gamme : changer de ton, modifier sa manière de parler ou d'agir.
6 Allez, votre douceur entretient sa folie. S'il vous eût vu tantôt lui parler vertement, Il craindrait vos transports et mon ressentiment (…) Ne t'afflige point tant; va, ma petite femme, Je m'en vais le trouver, et lui chanter sa gamme.
Molière, l'École des maris, II, 7.
2 (1837). Par anal. Succession, série (de couleurs, de teintes…) en gradation naturelle. || Gamme des couleurs (cit. 21). || Une gamme de nuances, de tons (→ Dégradation, cit. 4; étinceler, cit. 11, Gautier). || Couturier, peintre utilisant toute la gamme des gris, du bleu.
7 (…) la nature ne peut pas commettre de fautes dans l'arrangement de ses tons (…) Le vrai coloriste ne peut pas en commettre non plus; et tout lui est permis, parce qu'il connaît de naissance la gamme des tons, la force du ton (…)
Baudelaire, Curiosités esthétiques, Salon de 1846, III.
8 Voyez ces gris fins, ces verts tendres, ces terrains neutres, toute cette gamme éteinte et douce qui est celle de nos climats.
Th. Gautier, Souvenirs de théâtre, De Ziem.
9 (…) le goût d'une matière liée souvent à une gamme qui va du blanc au brun en passant par les ocres, et qu'a retrouvée parfois Derain.
Malraux, les Voix du silence, p. 194.
♦ (1973). Techn. || Gamme de fréquences : ensemble continu de fréquences pour lesquelles les oscillations ou les ondes ont des propriétés comparables. Intervalle de fréquences dans lequel un appareil peut être réglé.
3 (1840, Gautier). Série continue où tous les degrés, toutes les espèces sont représentés. || Psychologue qui prétend analyser toute la gamme des sentiments. || La gamme des nuances de la jalousie dans l'œuvre de Proust. || Joueur de tennis exécutant toute la gamme des coups difficiles. || Cave de connaisseur où figure la gamme entière des vins de Bourgogne. || Étonnante gamme d'expressions sur le visage d'un mime. — ☑ Fam. Toute la gamme ! : du premier jusqu'au dernier.
10 Nous suivîmes toute la gamme, depuis le jérès de quatre-vingts ans (…) jusqu'au jérès sec (…) Entre ces deux notes extrêmes, il y a tout un registre de vins intermédiaires.
Gautier, Voyage en Espagne, p. 270.
11 Et n'est-ce pas bien cela qu'exprime leur bizarre poésie de sons qui, tout en ayant l'air inintelligible, essaye de chanter en effet la gamme entière des sensations et de noter par les voisinages des mots, bien plus que par leur accord rationnel et leur signification connue, d'intraduisibles sens, qui sont obscurs pour nous, et clairs pour eux ?
Maupassant, la Vie errante, La nuit.
12 La charité, l'indulgence, la mansuétude, voilà toute une gamme de vertus qu'il me faut acquérir.
G. Duhamel, Salavin, IV, 27 janv.
♦ Comm., publ. Série (de produits commercialisés) considérée comme cohérente et classée selon les utilisations, les prix, etc. || Produits présentés de manière différente « en gamme industrielle (et) en gamme militaire » (Inter électronique, no 163, 24 févr. 1975, p. 27). — ☑ Loc. Haut de gamme, bas de gamme : produits les plus chers, les moins chers, dans une telle série. || « Les voitures de 6-7 CV, les “bas de gamme” des constructeurs » (l'Express, 13 oct. 1979). — En appos. || Une voiture, un réfrigérateur haut de gamme. || Téléviseurs, récepteurs haut de gamme. — REM. Dans cet usage, et pour des raisons sociologiquement évidentes, bas de gamme est fort peu employé, haut de gamme devenant un synonyme prétentieux de « de qualité ».
Encyclopédie Universelle. 2012.