- ЯДРО АТОМНОЕ
-
центральная массивная часть атома, состоящая из протонов и нейтронов (нуклонов). Масса Я. а. примерно в 4 •103 раз больше массы всех входящих в состав атома эл-нов. Размеры Я. а. составляют = 10-12—10=13 см. Электрич. заряд положителен и по абс. величине равен сумме зарядов ат. эл-нов нейтрального атома. Я. а. было открыто англ. физиком Э. Резерфордом в 1911 в опытах по рассеянию a-частиц при прохождении их через вещество. Обнаружив, что a-частицы чаще, чем ожидалось, рассеиваются на большие углы, Резерфорд предположил, что положит. заряд атома сосредоточен в малом по размерам Я. а. (до этого господствовали представления англ. физика Дж. Дж. Томсона, согласно к-рым положит. заряд атома равномерно распределён по его объёму). Идея Резерфорда была принята его современниками не сразу (гл. препятствием была убеждённость в неизбежном падении ат. эл-нов на ядро из-за потерь энергии на эл.-магн. излучение при движении по орбите вокруг Я. а.). Большую роль в её признании сыграла работа дат. физика Н. Бора (1913), положившая начало квант. теории атома (см. АТОМ). В кон. 1913 ученик Резерфорда англ. физик Г. Мозли показал экспериментально, что электрич. заряд Я. а. (в ед. абс. величины заряда эл-на е) равен порядковому номеру Z элемента в периодич. системе элементов. После Мозли факт существования Я. а. утвердился в физике окончательно.Характеристики ядраСостав ядра. Ко времени открытия Я. а. были известны только две элементарные частицы — протон и электрон. В соответствии с этим считалось вероятным, что Я. а. из них состоит. Однако в кон. 20-х гг. протонно-электронная гипотеза столкнулась с серьёзной трудностью, получившей название азотной катастрофы: по протонно-электронной гипотезе, ядро азота должно было содержать 21 частицу (14 протонов и 7 эл-нов), спин каждой из к-рых равен 1/2. Спин ядра азота должен был быть полуцелым, а, согласно опытным данным (по оптич. молекулярным спектрам), он оказался равным 1. Состав Я. а. был выяснен после открытия англ. физиком Дж. Чедвиком (1932) нейтрона со спином (установлено позже) 1/2. Идея о том, что Я. а. состоит из протонов и нейтронов, была впервые высказана в печати Д. Д. Иваненко (1932) и непосредственно вслед за этим развита нем. физиком В. Гейзенбергом (1932). Предположение о протонно-нейтронном составе ядра получило в дальнейшем полное эксперим. подтверждение.В совр. яд. физике протон (р) и нейтрон (n) объединяются общим названием «нуклон» (N). Общее число нуклонов в Я. а. наз. массовым числом А, число протонов равно заряду ядра Z, число нейтронов N=A-Z. У ядер-изотопов одно и то же Z, но разные А и N, у ядер-и з о б а р одинаковое А и разные Z и N. В связи с открытием ну к лонных изобар (см. РЕЗОНАНСЫ) выяснилось, что внутриядерные нуклоны, взаимодействуя друг с другом, могут превращаться в нуклонные изобары. В простейшем ядре— дейтроне, состоящем из одного протона и одного нейтрона, нуклоны примерно 1% времени должны пребывать в виде нуклонных изобар. Периодически на короткое время (=10-23—10-24 с) в ядрах появляются мезоны, в т. ч. пи-мезоны. Вз-ствие нуклонов сводится к многократным актам испускания p-мезона одним из нуклонов и поглощения его другим. Возникающие обменные мезонные токи сказываются, в частности, на эл.-магн. свойствах ядер.Взаимодействие нуклонов.Силы, удерживающие нуклоны в ядре, наз. ядерными. Они явл. проявлением самых интенсивных из всех известных в физике вз-ствий (см. СИЛЬНОЕ ВЗАИМОДЕЙСТВИЕ). Яд. силы, действующие между двумя протонами в ядре, по порядку величины в сто раз интенсивнее электростатич. вз-ствия между ними. Важным свойством яд. сил явл. их изотопическая инвариантность, т. е. независимость от зарядового состояния нуклонов: яд. вз-ствия двух протонов, двух нейтронов или нейтрона и протона одинаковы, если одинаковы состояния относит. движения этих пар ч-ц и их спиновые состояния. Интенсивность яд. сил зависит от расстояния между нуклонами, от взаимной ориентации их спинов, от ориентации спинов относительно орбитального момента и радиуса-вектора, проведённого от одной ч-цы к другой. В соответствии с этим различают центральные силы, спин-спиновые, спин-орбитальные и тензорные.Яд. силы характеризуются определённым радиусом действия, он определяется комптоновской длиной волны p-мезонов, к-рыми обмениваются нуклоны в процессе яд. вз-ствия: r0=R/mc, где m — масса p-мезона. Наибольший радиус действия имеют силы, обусловленные обменом p-мезонами. Для них r0=1,41 Ф (1Ф=10-13 см). Межнуклонные расстояния в ядрах имеют именно такой порядок величины, однако существенный вклад в яд. силы вносит обмен и более тяжёлыми мезонами. Точная зависимость яд. сил от расстояния между двумя нуклонами и относит. интенсивность яд. сил разного типа с определённостью не установлены. В многонуклонных ядрах возможны силы, к-рые не сводятся к вз-ствию только пар нуклонов. Роль т. н. многочастичных с и л в структуре ядер пока не выяснена.Размеры ядер зависят от числа содержащихся в них нуклонов. Средняя плотность числа нуклонов в ядре (их число в ед. объёма) для всех многонуклонных ядер (А >10) практически одинакова. Это означает, что объём ядра пропорц. числу нуклонов А , а его линейный размер пропорц. A1/3. Эфф. радиус ядра R даётся формулой:R=аА1/3, (1)где константа а близка к радиусу действия яд. сил r0 и зависит от того, в каких физ. явлениях измеряется R. В случае т. н. зарядового радиуса ядра, измеряемого по рассеянию эл-нов на ядрах или по положению уровней энергии m-мезоатомов,— a=1,12 Ф. Эфф. радиус, определённый из процессов вз-ствий адронов с ядрами (нуклонов, мезонов, a-частиц и др.), оказывается неск. больше зарядового: а=1,2—1,4 Ф.Плотность яд. в-ва чрезвычайно велика по сравнению с плотностью обычных в-в и составляет ок. 1014 г/см3. Плотность числа нуклонов в ядре r почти постоянна в центральной части ядра и экспоненциально убывает на периферии. Для приближённого описания эмпирич. данных иногда принимают след. зависимость r от расстояния r до центра ядра:r(r)=r0/(1+exp(r-Rc)/b (2)Эфф. радиус ядра R равен при этом R0+b; величина b характеризует размытость границы ядра и почти одинакова для всех ядер (b»0,5 Ф). Параметр r0— удвоенная плотность на «границе» ядраr0=2r(R0)определяется из условия нормировки (равенства объёмного интеграла от r числу нуклонов А).Из ф-лы (1) следует, что размеры ядер варьируются по порядку величины от 10-13 см (1Ф) до 10-12 см (10 Ф) для тяжёлых ядер. Однако формула (1) описывает рост линейных размеров ядер с увеличением числа нуклонов лишь огрублённо при б. или м. значит. увеличении А. Изменение же размера ядра в случае присоединения к нему одного или двух нуклонов зависит от деталей структуры ядра и может быть иррегулярным. В частности (как показали измерения изотопич. сдвига ат. уровней энергии), иногда радиус ядра при добавлении двух нейтронов даже уменьшается.Энергия связи и масса ядра. Энергия связи ядра ?св — это энергия, к-рую необходимо затратить, чтобы расщепить ядро на отд. нуклоны. Она равна разности суммы масс входящих в него нуклонов и массы ядра, умноженной на с2.?св=(Zmр+Nmn-М)с2.Здесь mр, mn и М — массы протона, нейтрона и ядра.Замечательной особенностью Я. а. явл. тот факт, что ?св приблизительно пропорц. числу нуклонов в ядре, так что удельная энергия связи ?св/А слабо меняется при изменении А (для большинства ядер ?св/А»6—8 МэВ). Это свойство, наз. насыщением ядерных сил, означает, что каждый нуклон эффективно связывается не со всеми нуклонами ядра (в этом случае энергия связи была бы пропорц. A2 при A->1), а лишь с нек-рыми из них. Теоретически это возможно, если силы при изменении расстояния изменяют знак (притяжение на одних расстояниях сменяется отталкиванием на других).Зависимость ?св от А и Z для всех известных ядер приближённо описывается полуэмпирич. массовой ф-лой (впервые предложенной нем. физиком К. Ф. Вейцзеккером в 1935):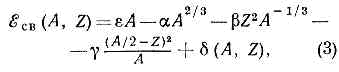 . где a, b и g — постоянные, имеющие размерность энергии. Первое, и наибольшее, слагаемое определяет линейную зависимость энергии связи от А ', второй член, уменьшающий энергию связи, обусловлен тем, что часть нуклонов находится на поверхности ядра; третье слагаемое — энергия электростатич. кулоновского отталкивания протонов (обратно пропорц. радиусу ядра и пропорц. квадрату его заряда); четвёртое слагаемое учитывает влияние на энергию связи неравенства числа протонов и нейтронов в ядре и, наконец, пятое слагаемое зависит от чётности чисел А и Z:
. где a, b и g — постоянные, имеющие размерность энергии. Первое, и наибольшее, слагаемое определяет линейную зависимость энергии связи от А ', второй член, уменьшающий энергию связи, обусловлен тем, что часть нуклонов находится на поверхности ядра; третье слагаемое — энергия электростатич. кулоновского отталкивания протонов (обратно пропорц. радиусу ядра и пропорц. квадрату его заряда); четвёртое слагаемое учитывает влияние на энергию связи неравенства числа протонов и нейтронов в ядре и, наконец, пятое слагаемое зависит от чётности чисел А и Z: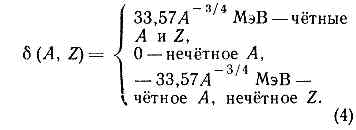 . Эта сравнительно небольшая поправка оказывается, однако, весьма существенной для ряда явлений, и в частности для деления тяжёлых ядер. Именно она определяет делимость ядер нечётных по А изотопов урана под действием медленных нейтронов (см. ДЕЛЕНИЕ АТОМНОГО ЯДРА), что и обусловливает выделенную роль этих изотопов в яд. энергетике (см. ЯДЕРНОЕ ТОПЛИВО). Оптим. согласие с опытом достигается при e=14,03 МэВ, a=13,03 МэВ, b=0,5835 МэВ, g=77,25 МэВ. Формулы (3) и (4) могут быть использованы для оценки энергий связи ядер, не слишком удалённых от полосы стабильности. Последняя определяется положением максимума ?св как ф-ции Z при фиксированном А. Это условие определяет связь между Z и А для стабильных ядер:Z=A (1,98+0,15A2/3)-1. (5)Ф-ла (3) не учитывает квант. эффектов, связанных с деталями структуры ядер, к-рые могут приводить к скачкообразным изменениям ?св вблизи нек-рых значений А и Z (см. ниже). Структурные особенности в зависимости ?св от А и Z существенны в вопросе о предельно возможном значении Z, т. е. о границе периодической системы элементов. Эта граница обусловлена неустойчивостью тяжёлых ядер относительно процесса деления. Теор. оценки вероятности спонтанного деления ядер не исключают возможности существования «островов стабильности» сверхтяжёлых ядер вблизи Z=114 и Z=126 (см. ТРАНСУРАНОВЫЕ ЭЛЕМЕНТЫ).Квантовые характеристики ядерных уровней.Я. а. может находиться лишь в определённых дискр. квант. состояниях, отличающихся друг от друга энергией и др. сохраняющимися во времени физ. величинами. Важнейшие квант. хар-ки яд. состояния — спин I и чётность Р. Спин I (в ед. ћ)— целое число у ядер с чётным А и полуцелое при нечётном А (спин Я. а. равен сумме спинов составляющих его нуклонов). Чётность состояния Р=±1 указывает на изменение знака волновой функции ядра при зеркальном отражении пространства (см. ПРОСТРАНСТВЕННАЯ ИНВЕРСИЯ). Эти две хар-ки часто объединяют единым символом IР или I± Имеет место след. эмпирич. правило: для осн. состояний ядер (с наименьшей энергией) с чётными А и Z Ip=0+ . Квант. состояние системы имеет определённую чётность Р, если система зеркально симметрична (т. е. переходит сама в себя при зеркальном отражении). В ядрах зеркальная симметрия неск. нарушена наличием слабого взаимодействия между нуклонами, не сохраняющего чётность (его интенсивность по порядку величины =10-5% от осн. сил, связывающих нуклоны в ядрах). Однако обусловленное слабым вз-ствием смешивание состояний с разной чётностью мало и практически не сказывается на структуре ядер.Помимо I и Р, яд. состояния характеризуются также квант. числами, возникающими вследствие динамич. симметрии яд. вз-ствий. Важнейшая из них — изотопическая инвариантность яд. сил. Она приводит к появлению у лёгких ядер (Z?20) квант. числа Т, назв. изотопическим спином; Т — целое число при чётном А и полуцелое при нечётном (т. к. изотопич. спин нуклона равен 1/2). Разл. состояния ядра могут иметь разный изоспин:T>=(A-2Z)/2. (6)Опыт показывает, что изоспины осн. состояний ядер минимальны и равны (A-2Z)/2. Изоспин характеризует свойства симметрии волновой ф-ции состояния ядра относительно замены p«n. С изоспином связано существование изотопич. яд. мультиплетов, или аналоговых состояний, у ядер с одним и тем же А. Аналоговые состояния, хотя и относятся к разным ядрам (разные Z), но имеют одинаковую структуру и, следовательно, одинаковые IР и Т. Число таких состояний равно 2T+1. Легчайшее после протона ядро — дейтрон—имеет изоспин Т=0 и поэтому не имеет аналогов. Ядра 31Н и 32Не образуют изотопич. дублет с T=1/2. Для более тяжёлых ядер членами одного изотопич, мультиплета явл. как основные, так и возбуждённые состояния ядер. Это связано с тем, что при увеличении Z растёт кулоновская энергия ядра (она растёт с числом протонов) и, кроме того, при замене р«n на полной энергии ядра сказывается разность масс протона и нейтрона. Примером изотопич. мультиплета, содержащего как основные, так и возбуждённые состояния, явл. триплет с Т=1: 146С (осн) — 147N* (энергия возбуждения 2,31 МэВ) — 148О (осн). Полуразность числа нейтронов и протонов T3 наз. проекцией изоспина. Для членов изотопического мультиплета T3 принимает (2T+1) значений, отличающихся друг от друга на единицу и лежащих в интервале -T?T3?+T. Величина Т3 для ядер определена так, что для протона T3=-1/2, а для нейтрона T3=+1/2. В физике же элементарных частиц протону приписывается положит. значение Т3, а нейтрону — отрицательное. Это чисто условное различие в определениях вызвано соображениями удобства (при избранном в яд. физике определении T3 эта величина положительна для подавляющего числа ядер). Для тяжёлых ядер изоспин не явл. хорошим квантовым числом (состояния с разным изоспином смешиваются гл. обр. электростатич. вз-ствием протонов). Тем не менее ощутимые следы изотопич. симметрии остаются и в этом случае. Она проявляется, в частности, в наличии т. н. аналоговых резонансов (аналоговых состояний, нестабильных относительно распада с испусканием нуклонов).Кроме I, Р и Т, яд. состояния могут характеризоваться также квант. числами, связанными с конкретной динамич. моделью, привлекаемой для приближённого описания ядра (см. ниже).Электрические и магнитные моменты ядер.В разл. состояниях ядро может иметь разные по величине магн. дипольные и электрич. квадрупольные моменты. Квадрупольные моменты ядер могут быть отличны от нуля только в том случае, когда спин I>1/2. Яд. состояние с определённой чётностью Р не может обладать отличным от нуля электрич. дипольным моментом. Более того, даже при несохранении чётности для возникновения электрич. дипольного момента необходимо, чтобы вз-ствие нуклонов было необратимо по времени (Т — неинвариантно). Поскольку по опытным данным T-неинвариантные межнуклонные силы (если они вообще есть) по меньшей мере в тысячу раз слабее осн. яд. сил, а эффекты несохранения чётности также очень малы, то электрич. дипольные моменты либо равны нулю, либо столь малы, что их обнаружение находится вне пределов возможностей совр. яд. эксперимента. Яд. магн. дипольные моменты имеют порядок величины яд. магнетона. Электрич. квадрупольные моменты eQ изменяются в очень широких пределах: от величины порядка е•10-27 см2 (лёгкие ядра) до е•10-23 см2 (тяжёлые ядра); обычно для них указываются просто значения Q, измеренные в см2 (см. КВАДРУПОЛЬНЫЙ МОМЕНТ ЯДРА). В большинстве случаев известны лишь статич. моменты осн. состояний, поскольку они могут быть измерены оптич. и радиоспектроскопич. методами (см. ЯДЕРНЫЙ МАГНИТНЫЙ РЕЗОНАНС). Значения статич. электрич. и магн. моментов существенно зависят от структуры ядра, распределения в нём зарядов и токов. Объяснение наблюдаемых величин магн. дипольных и электрич. квадрупольных моментов явл. пробным камнем для любой физ. модели ядра.Структура и модели ядерМногочастичная квант. система с сильным вз-ствием, каковой явл. ядро, с теор. точки зрения—объект исключительно сложный. Трудности связаны не только с вычислениями физ. величин, характеризующих ядро, но и с качеств. пониманием свойств яд. состояний, спектра энергетич. уровней, механизма ядерных реакций. Тяжёлые ядра содержат много нуклонов, но всё же их число не столь велико, чтобы можно было с уверенностью воспользоваться методами статистич. физики, как в теории конденсированных сред (жидкости, твёрдые тела). К матем. трудностям теории добавляется недостаточная определённость данных о яд. силах. Поскольку межнуклонное вз-ствие сводится к обмену p-мезонами, объяснение свойств ядра в конечном счёте должно опираться на релятив. квант. теорию элементарных ч-ц, к-рая сама по себе в совр. её состоянии несвободна от внутр. противоречий и не может считаться завершённой. Хотя сравнительно небольшие в среднем скорости нуклонов в ядре (=0,1 с) неск. упрощают теорию, позволяя строить её в первом приближении на основе нерелятив. кьантоеой механики, яд. задача мн. тел остаётся пока одной из фундаментальных проблем совр. физики. По всем этим причинам до сих пор, исходя из «первых принципов», рассматривалась только структура простейших ядер — дейтрона, 3Н и 3Не. Структуру более сложных ядер исследуют с помощью моделей.Оболочечная модель.Каждый нуклон находится в ядре в определённом квант. состоянии, характеризуемом энергией, спином j, его проекцией т на одну из координатных осей и орбитальным моментом l=j±1/2; чётность состояния нуклона р=(-1)l. Энергия уровня не зависит от проекции орбитального момента на выделенное направление. Поэтому в соответствии с Паули принципом на каждом уровне энергии с моментами j, l может находиться (2j + 1) тождеств. нуклонов, образующих «оболочку» (j, l). Полный орбитальный момент заполненной оболочки равен нулю. Поэтому если ядро составлено только из заполненных протонных и нейтронных оболочек, то его спин будет также равен нулю. Всякий раз, когда количество протонов или нейтронов в ядре достигает числа, отвечающего заполнению очередной оболочки, происходит скачкообразное изменение нек-рых характеризующих ядро величин (в частности, энергии связи). Это создаёт подобие периодичности в свойствах ядер в зависимости от А и Z, аналогичной периодич. закону для атомов. В обоих случаях физ. причиной периодичности явл. принцип Паули, согласно к-рому два тождественных фермиона не могут находиться в одном и том же состоянии. Однако оболочечная структура ядер проявляется значительно слабее, чем в атомах. В ядрах индивидуальные квант. состояния ч-ц («орбиты») возмущаются вз-ствием («столкновениями») их друг с другом гораздо сильнее, чем в атомах. Более того, известно, что большое число яд. состояний совсем не похоже на совокупность движущихся в ядре независимо друг от друга нуклонов, т. е. не может быть объяснено в рамках оболочечной модели. Наличие таких коллективных состояний указывает на то, что представления об индивидуальных нуклонных состояниях — скорее, методич. базис, удобный для описания нек-рых состояний ядра, чем физ. реальность. В этой связи в оболочечную модель вводится понятие квазичастиц. Ядро уподобляется «конечной» ферми-жидкости (см. КВАНТОВАЯ ЖИДКОСТЬ), а ядро в осн. состоянии рассматривается как вырожденный ферми-газ квазичастиц, к-рые эффективно не взаимодействуют друг с другом, поскольку всякий акт столкновения, изменяющий индивидуальные состояния квазичастиц, запрещён принципом Паули. В возбуждённом состоянии ядра, когда 1 или 2 квазичастицы находятся на более высоких уровнях энергии, они, освободив орбиты внутри ферми-сферы (см. ФЕРМИ ПОВЕРХНОСТЬ), могут взаимодействовать как друг с другом, так и с образовавшейся дыркой в нижней оболочке. В результате этого вз-ствия может происходить переход квазичастиц из заполненных состояний в незаполненные, вследствие чего старая дырка исчезает, а новая появляется, что эквивалентно перемещению дырки по спектру состояний. Т. о., согласно оболочечной модели, основывающейся на теории ферми-жидкости, спектр нижних возбуждённых состояний ядер определяется движением 1 — 2 квазичастиц вне ферми-сферы и вз-ствием их друг с другом и с дырками внутри ферми-сферы. Этим самым объяснение структуры многонуклонного ядра при небольших энергиях возбуждения фактически сводится к квант. проблеме 2—4 взаимодействующих тел (квазичастица — дырка или 2 квазичастицы — 2 дырки). Применение теории ферми-жидкости , к Я. а. было развито А. Б. Мигдалом (1965). Трудность теории состоит, однако, в том, что вз-ствие квазичастиц и дырок не мало, и потому нет уверенности в невозможности появления низкоэнергетич. возбуждённого состояния, обусловленного большим числом квазичастиц вне ферми-сферы.В др. вариантах оболочечной модели движение квазичастиц по независимым «орбитам» даже в осн. состоянии ядра рассматривается лишь как первое приближение к действительности. Для уточнения вводится эфф. вз-ствие между квазичастицами в каждой оболочке, приводящее к перемешиванию первонач. конфигураций индивидуальных состояний. Это вз-ствие учитывается по методу теории возмущений (справедливой при малости возмущения). Однако при этом эфф. вз-ствие, необходимое для описания опытных фактов, оказывается не слабым. Кроме того, в разных оболочках приходится вводить разные эфф. вз-ствия, что увеличивает число эмпирически подбираемых параметров модели. Упомянутые осн. варианты модели оболочек модифицируются иногда введением дополнит. вз-ствий (напр., вз-ствия квазичастиц с колебаниями поверхности ядра) для достижения лучшего согласия теории и опыта.Т. о., совр. оболочечная модель ядра фактически явл. полуэмпирич. схемой, позволяющей понять нек-рые закономерности в структуре ядер, но не способной последовательно количественно описать свойства ядер. В частности, не просто выяснить чисто теоретически порядок заполнения оболочек, а следовательно и магич. числа, к-рые служили бы аналогами периодов таблицы Менделеева для атомов. Порядок заполнения оболочек зависит, во-первых, от хар-ра того силового поля, к-рое определяет индивидуальные состояния квазичастиц, и, во-вторых, от смешивания конфигураций. Последнее обычно принимается во внимание лишь для незаполненных оболочек. Наблюдаемые на опыте магич. числа нейтронов (2, 8, 20, 28, 40, 50, 82, 126) и протонов (2, 8, 20, 28, 50, 82) отвечают квант. состояниям квазичастиц, движущихся в прямоугольной или осцилляторной потенц. яме со спин-орбитальным взаимодействием (именно благодаря ему возникают числа 28, 40, 82 и 126).
. Эта сравнительно небольшая поправка оказывается, однако, весьма существенной для ряда явлений, и в частности для деления тяжёлых ядер. Именно она определяет делимость ядер нечётных по А изотопов урана под действием медленных нейтронов (см. ДЕЛЕНИЕ АТОМНОГО ЯДРА), что и обусловливает выделенную роль этих изотопов в яд. энергетике (см. ЯДЕРНОЕ ТОПЛИВО). Оптим. согласие с опытом достигается при e=14,03 МэВ, a=13,03 МэВ, b=0,5835 МэВ, g=77,25 МэВ. Формулы (3) и (4) могут быть использованы для оценки энергий связи ядер, не слишком удалённых от полосы стабильности. Последняя определяется положением максимума ?св как ф-ции Z при фиксированном А. Это условие определяет связь между Z и А для стабильных ядер:Z=A (1,98+0,15A2/3)-1. (5)Ф-ла (3) не учитывает квант. эффектов, связанных с деталями структуры ядер, к-рые могут приводить к скачкообразным изменениям ?св вблизи нек-рых значений А и Z (см. ниже). Структурные особенности в зависимости ?св от А и Z существенны в вопросе о предельно возможном значении Z, т. е. о границе периодической системы элементов. Эта граница обусловлена неустойчивостью тяжёлых ядер относительно процесса деления. Теор. оценки вероятности спонтанного деления ядер не исключают возможности существования «островов стабильности» сверхтяжёлых ядер вблизи Z=114 и Z=126 (см. ТРАНСУРАНОВЫЕ ЭЛЕМЕНТЫ).Квантовые характеристики ядерных уровней.Я. а. может находиться лишь в определённых дискр. квант. состояниях, отличающихся друг от друга энергией и др. сохраняющимися во времени физ. величинами. Важнейшие квант. хар-ки яд. состояния — спин I и чётность Р. Спин I (в ед. ћ)— целое число у ядер с чётным А и полуцелое при нечётном А (спин Я. а. равен сумме спинов составляющих его нуклонов). Чётность состояния Р=±1 указывает на изменение знака волновой функции ядра при зеркальном отражении пространства (см. ПРОСТРАНСТВЕННАЯ ИНВЕРСИЯ). Эти две хар-ки часто объединяют единым символом IР или I± Имеет место след. эмпирич. правило: для осн. состояний ядер (с наименьшей энергией) с чётными А и Z Ip=0+ . Квант. состояние системы имеет определённую чётность Р, если система зеркально симметрична (т. е. переходит сама в себя при зеркальном отражении). В ядрах зеркальная симметрия неск. нарушена наличием слабого взаимодействия между нуклонами, не сохраняющего чётность (его интенсивность по порядку величины =10-5% от осн. сил, связывающих нуклоны в ядрах). Однако обусловленное слабым вз-ствием смешивание состояний с разной чётностью мало и практически не сказывается на структуре ядер.Помимо I и Р, яд. состояния характеризуются также квант. числами, возникающими вследствие динамич. симметрии яд. вз-ствий. Важнейшая из них — изотопическая инвариантность яд. сил. Она приводит к появлению у лёгких ядер (Z?20) квант. числа Т, назв. изотопическим спином; Т — целое число при чётном А и полуцелое при нечётном (т. к. изотопич. спин нуклона равен 1/2). Разл. состояния ядра могут иметь разный изоспин:T>=(A-2Z)/2. (6)Опыт показывает, что изоспины осн. состояний ядер минимальны и равны (A-2Z)/2. Изоспин характеризует свойства симметрии волновой ф-ции состояния ядра относительно замены p«n. С изоспином связано существование изотопич. яд. мультиплетов, или аналоговых состояний, у ядер с одним и тем же А. Аналоговые состояния, хотя и относятся к разным ядрам (разные Z), но имеют одинаковую структуру и, следовательно, одинаковые IР и Т. Число таких состояний равно 2T+1. Легчайшее после протона ядро — дейтрон—имеет изоспин Т=0 и поэтому не имеет аналогов. Ядра 31Н и 32Не образуют изотопич. дублет с T=1/2. Для более тяжёлых ядер членами одного изотопич, мультиплета явл. как основные, так и возбуждённые состояния ядер. Это связано с тем, что при увеличении Z растёт кулоновская энергия ядра (она растёт с числом протонов) и, кроме того, при замене р«n на полной энергии ядра сказывается разность масс протона и нейтрона. Примером изотопич. мультиплета, содержащего как основные, так и возбуждённые состояния, явл. триплет с Т=1: 146С (осн) — 147N* (энергия возбуждения 2,31 МэВ) — 148О (осн). Полуразность числа нейтронов и протонов T3 наз. проекцией изоспина. Для членов изотопического мультиплета T3 принимает (2T+1) значений, отличающихся друг от друга на единицу и лежащих в интервале -T?T3?+T. Величина Т3 для ядер определена так, что для протона T3=-1/2, а для нейтрона T3=+1/2. В физике же элементарных частиц протону приписывается положит. значение Т3, а нейтрону — отрицательное. Это чисто условное различие в определениях вызвано соображениями удобства (при избранном в яд. физике определении T3 эта величина положительна для подавляющего числа ядер). Для тяжёлых ядер изоспин не явл. хорошим квантовым числом (состояния с разным изоспином смешиваются гл. обр. электростатич. вз-ствием протонов). Тем не менее ощутимые следы изотопич. симметрии остаются и в этом случае. Она проявляется, в частности, в наличии т. н. аналоговых резонансов (аналоговых состояний, нестабильных относительно распада с испусканием нуклонов).Кроме I, Р и Т, яд. состояния могут характеризоваться также квант. числами, связанными с конкретной динамич. моделью, привлекаемой для приближённого описания ядра (см. ниже).Электрические и магнитные моменты ядер.В разл. состояниях ядро может иметь разные по величине магн. дипольные и электрич. квадрупольные моменты. Квадрупольные моменты ядер могут быть отличны от нуля только в том случае, когда спин I>1/2. Яд. состояние с определённой чётностью Р не может обладать отличным от нуля электрич. дипольным моментом. Более того, даже при несохранении чётности для возникновения электрич. дипольного момента необходимо, чтобы вз-ствие нуклонов было необратимо по времени (Т — неинвариантно). Поскольку по опытным данным T-неинвариантные межнуклонные силы (если они вообще есть) по меньшей мере в тысячу раз слабее осн. яд. сил, а эффекты несохранения чётности также очень малы, то электрич. дипольные моменты либо равны нулю, либо столь малы, что их обнаружение находится вне пределов возможностей совр. яд. эксперимента. Яд. магн. дипольные моменты имеют порядок величины яд. магнетона. Электрич. квадрупольные моменты eQ изменяются в очень широких пределах: от величины порядка е•10-27 см2 (лёгкие ядра) до е•10-23 см2 (тяжёлые ядра); обычно для них указываются просто значения Q, измеренные в см2 (см. КВАДРУПОЛЬНЫЙ МОМЕНТ ЯДРА). В большинстве случаев известны лишь статич. моменты осн. состояний, поскольку они могут быть измерены оптич. и радиоспектроскопич. методами (см. ЯДЕРНЫЙ МАГНИТНЫЙ РЕЗОНАНС). Значения статич. электрич. и магн. моментов существенно зависят от структуры ядра, распределения в нём зарядов и токов. Объяснение наблюдаемых величин магн. дипольных и электрич. квадрупольных моментов явл. пробным камнем для любой физ. модели ядра.Структура и модели ядерМногочастичная квант. система с сильным вз-ствием, каковой явл. ядро, с теор. точки зрения—объект исключительно сложный. Трудности связаны не только с вычислениями физ. величин, характеризующих ядро, но и с качеств. пониманием свойств яд. состояний, спектра энергетич. уровней, механизма ядерных реакций. Тяжёлые ядра содержат много нуклонов, но всё же их число не столь велико, чтобы можно было с уверенностью воспользоваться методами статистич. физики, как в теории конденсированных сред (жидкости, твёрдые тела). К матем. трудностям теории добавляется недостаточная определённость данных о яд. силах. Поскольку межнуклонное вз-ствие сводится к обмену p-мезонами, объяснение свойств ядра в конечном счёте должно опираться на релятив. квант. теорию элементарных ч-ц, к-рая сама по себе в совр. её состоянии несвободна от внутр. противоречий и не может считаться завершённой. Хотя сравнительно небольшие в среднем скорости нуклонов в ядре (=0,1 с) неск. упрощают теорию, позволяя строить её в первом приближении на основе нерелятив. кьантоеой механики, яд. задача мн. тел остаётся пока одной из фундаментальных проблем совр. физики. По всем этим причинам до сих пор, исходя из «первых принципов», рассматривалась только структура простейших ядер — дейтрона, 3Н и 3Не. Структуру более сложных ядер исследуют с помощью моделей.Оболочечная модель.Каждый нуклон находится в ядре в определённом квант. состоянии, характеризуемом энергией, спином j, его проекцией т на одну из координатных осей и орбитальным моментом l=j±1/2; чётность состояния нуклона р=(-1)l. Энергия уровня не зависит от проекции орбитального момента на выделенное направление. Поэтому в соответствии с Паули принципом на каждом уровне энергии с моментами j, l может находиться (2j + 1) тождеств. нуклонов, образующих «оболочку» (j, l). Полный орбитальный момент заполненной оболочки равен нулю. Поэтому если ядро составлено только из заполненных протонных и нейтронных оболочек, то его спин будет также равен нулю. Всякий раз, когда количество протонов или нейтронов в ядре достигает числа, отвечающего заполнению очередной оболочки, происходит скачкообразное изменение нек-рых характеризующих ядро величин (в частности, энергии связи). Это создаёт подобие периодичности в свойствах ядер в зависимости от А и Z, аналогичной периодич. закону для атомов. В обоих случаях физ. причиной периодичности явл. принцип Паули, согласно к-рому два тождественных фермиона не могут находиться в одном и том же состоянии. Однако оболочечная структура ядер проявляется значительно слабее, чем в атомах. В ядрах индивидуальные квант. состояния ч-ц («орбиты») возмущаются вз-ствием («столкновениями») их друг с другом гораздо сильнее, чем в атомах. Более того, известно, что большое число яд. состояний совсем не похоже на совокупность движущихся в ядре независимо друг от друга нуклонов, т. е. не может быть объяснено в рамках оболочечной модели. Наличие таких коллективных состояний указывает на то, что представления об индивидуальных нуклонных состояниях — скорее, методич. базис, удобный для описания нек-рых состояний ядра, чем физ. реальность. В этой связи в оболочечную модель вводится понятие квазичастиц. Ядро уподобляется «конечной» ферми-жидкости (см. КВАНТОВАЯ ЖИДКОСТЬ), а ядро в осн. состоянии рассматривается как вырожденный ферми-газ квазичастиц, к-рые эффективно не взаимодействуют друг с другом, поскольку всякий акт столкновения, изменяющий индивидуальные состояния квазичастиц, запрещён принципом Паули. В возбуждённом состоянии ядра, когда 1 или 2 квазичастицы находятся на более высоких уровнях энергии, они, освободив орбиты внутри ферми-сферы (см. ФЕРМИ ПОВЕРХНОСТЬ), могут взаимодействовать как друг с другом, так и с образовавшейся дыркой в нижней оболочке. В результате этого вз-ствия может происходить переход квазичастиц из заполненных состояний в незаполненные, вследствие чего старая дырка исчезает, а новая появляется, что эквивалентно перемещению дырки по спектру состояний. Т. о., согласно оболочечной модели, основывающейся на теории ферми-жидкости, спектр нижних возбуждённых состояний ядер определяется движением 1 — 2 квазичастиц вне ферми-сферы и вз-ствием их друг с другом и с дырками внутри ферми-сферы. Этим самым объяснение структуры многонуклонного ядра при небольших энергиях возбуждения фактически сводится к квант. проблеме 2—4 взаимодействующих тел (квазичастица — дырка или 2 квазичастицы — 2 дырки). Применение теории ферми-жидкости , к Я. а. было развито А. Б. Мигдалом (1965). Трудность теории состоит, однако, в том, что вз-ствие квазичастиц и дырок не мало, и потому нет уверенности в невозможности появления низкоэнергетич. возбуждённого состояния, обусловленного большим числом квазичастиц вне ферми-сферы.В др. вариантах оболочечной модели движение квазичастиц по независимым «орбитам» даже в осн. состоянии ядра рассматривается лишь как первое приближение к действительности. Для уточнения вводится эфф. вз-ствие между квазичастицами в каждой оболочке, приводящее к перемешиванию первонач. конфигураций индивидуальных состояний. Это вз-ствие учитывается по методу теории возмущений (справедливой при малости возмущения). Однако при этом эфф. вз-ствие, необходимое для описания опытных фактов, оказывается не слабым. Кроме того, в разных оболочках приходится вводить разные эфф. вз-ствия, что увеличивает число эмпирически подбираемых параметров модели. Упомянутые осн. варианты модели оболочек модифицируются иногда введением дополнит. вз-ствий (напр., вз-ствия квазичастиц с колебаниями поверхности ядра) для достижения лучшего согласия теории и опыта.Т. о., совр. оболочечная модель ядра фактически явл. полуэмпирич. схемой, позволяющей понять нек-рые закономерности в структуре ядер, но не способной последовательно количественно описать свойства ядер. В частности, не просто выяснить чисто теоретически порядок заполнения оболочек, а следовательно и магич. числа, к-рые служили бы аналогами периодов таблицы Менделеева для атомов. Порядок заполнения оболочек зависит, во-первых, от хар-ра того силового поля, к-рое определяет индивидуальные состояния квазичастиц, и, во-вторых, от смешивания конфигураций. Последнее обычно принимается во внимание лишь для незаполненных оболочек. Наблюдаемые на опыте магич. числа нейтронов (2, 8, 20, 28, 40, 50, 82, 126) и протонов (2, 8, 20, 28, 50, 82) отвечают квант. состояниям квазичастиц, движущихся в прямоугольной или осцилляторной потенц. яме со спин-орбитальным взаимодействием (именно благодаря ему возникают числа 28, 40, 82 и 126).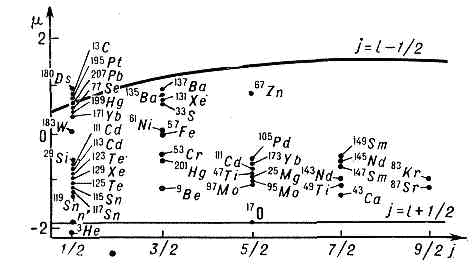 .
. 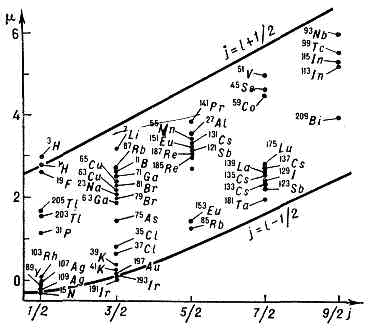 . Рис. 1 (слева). Линии Шмидта для ядер с нечётным числом нейтронов (точки — эксперим. данные).Рис. 2 (справа). Линии Шмидта для ядер с нечётным числом протонов.Объяснение самого факта существования магич. чисел было крупным успехом модели оболочек, впервые предложенной амер. физиком М. Гёпперт-Майер и нем. физиком Й. X. Д. Йенсеном в 1949—50. Др. важный результат модели оболочек даже в простейшей форме (без учёта вз-ствия квазичастиц) — получение квант. чисел IР осн. состояний нечётных ядер и приближённое описание данных о магн. дипольных моментах таких ядер. Согласно оболочечной модели, эти величины для нечётных ядер определяются состоянием (j, l) последнего «неспаренного» нуклона. В этом случае I=j, Р=(-1)l. Магн. дипольный момент 1 (в яд. магнетона х), если неспаренным нуклоном явл. нейтрон, равен:
. Рис. 1 (слева). Линии Шмидта для ядер с нечётным числом нейтронов (точки — эксперим. данные).Рис. 2 (справа). Линии Шмидта для ядер с нечётным числом протонов.Объяснение самого факта существования магич. чисел было крупным успехом модели оболочек, впервые предложенной амер. физиком М. Гёпперт-Майер и нем. физиком Й. X. Д. Йенсеном в 1949—50. Др. важный результат модели оболочек даже в простейшей форме (без учёта вз-ствия квазичастиц) — получение квант. чисел IР осн. состояний нечётных ядер и приближённое описание данных о магн. дипольных моментах таких ядер. Согласно оболочечной модели, эти величины для нечётных ядер определяются состоянием (j, l) последнего «неспаренного» нуклона. В этом случае I=j, Р=(-1)l. Магн. дипольный момент 1 (в яд. магнетона х), если неспаренным нуклоном явл. нейтрон, равен: . В случае неспаренного протона:
. В случае неспаренного протона: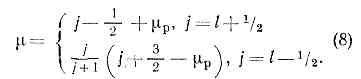 . Здесь mn=-1,913 и mр=2,793 — магн. моменты нейтрона и протона. Зависимости m от j при данном l=j±1/2 наз. линиями Шмидта. Магн. дипольные моменты практически всех нечётных ядер, согласно опытным данным, лежат между линиями Шмидта (рис. 1, 2), но не на них, как это требуется простейшей оболочечной моделью. Тем не менее близость эксперим. значений магн. дипольных моментов ядер к линиям Шмидта такова, что, зная j=I и m, можно в большинстве случаев однозначно определить I. Данные о квадрупольных электрич. моментах Q ядер значительно хуже описываются оболочечной моделью. Существенно, однако, что в зависимости Q от А и Z наблюдается периодичность, отвечающая магич. числам.Все эти сведения о Я. а. (значения I, Р, электрич. и магн. моменты осн. состояний, магич. числа, данные о возбуждённых состояниях) позволяют принять схему заполнения яд. оболочек, приведённую на рис. 3.Несферичность ядер. Ротационная модель.?=ћ2I(I+1)/2J, (9)где J — величина, практически не зависящая от I и имеющая размерность момента инерции. Спины возбуждённых состояний в (9) принимают, как показывает опыт, только чётные значения (2, 4, 6. . ., нулевое значение отвечает осн. состоянию).
. Здесь mn=-1,913 и mр=2,793 — магн. моменты нейтрона и протона. Зависимости m от j при данном l=j±1/2 наз. линиями Шмидта. Магн. дипольные моменты практически всех нечётных ядер, согласно опытным данным, лежат между линиями Шмидта (рис. 1, 2), но не на них, как это требуется простейшей оболочечной моделью. Тем не менее близость эксперим. значений магн. дипольных моментов ядер к линиям Шмидта такова, что, зная j=I и m, можно в большинстве случаев однозначно определить I. Данные о квадрупольных электрич. моментах Q ядер значительно хуже описываются оболочечной моделью. Существенно, однако, что в зависимости Q от А и Z наблюдается периодичность, отвечающая магич. числам.Все эти сведения о Я. а. (значения I, Р, электрич. и магн. моменты осн. состояний, магич. числа, данные о возбуждённых состояниях) позволяют принять схему заполнения яд. оболочек, приведённую на рис. 3.Несферичность ядер. Ротационная модель.?=ћ2I(I+1)/2J, (9)где J — величина, практически не зависящая от I и имеющая размерность момента инерции. Спины возбуждённых состояний в (9) принимают, как показывает опыт, только чётные значения (2, 4, 6. . ., нулевое значение отвечает осн. состоянию).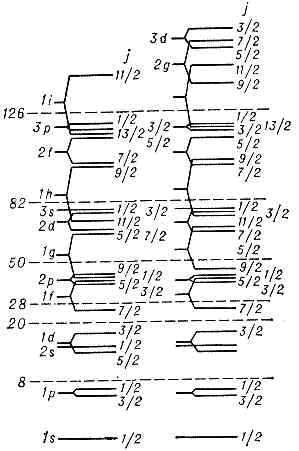 . Рис. 3. Эмпирич. последовательность уровней протонов и нейтронов в модели яд. оболочек. Справа от уровней указаны J, слева — спектроскопич. символ (буква отвечает определённому значению l, число — номер уровня с данным l; s, p, d, f, g, h, i соответственно означают l=0, 1, 2, 3, 4, 5, 6). Пунктиром отделены состояния, заполнение к-рых даёт магич. числа.Эти факты послужили основанием для построения ротационной модели несферич. ядра, впервые предложенной амер. физиком Дж. Рейнуотером (1950) и развитой в работах дат. физика О. Бора и амер. физика Б. Моттельсона. Согласно этой модели, ядро представляет собой эллипсоид вращения. Его большая (a1) и малая (а2) полуоси выражаются через параметр деформации b ядра след. образом:
. Рис. 3. Эмпирич. последовательность уровней протонов и нейтронов в модели яд. оболочек. Справа от уровней указаны J, слева — спектроскопич. символ (буква отвечает определённому значению l, число — номер уровня с данным l; s, p, d, f, g, h, i соответственно означают l=0, 1, 2, 3, 4, 5, 6). Пунктиром отделены состояния, заполнение к-рых даёт магич. числа.Эти факты послужили основанием для построения ротационной модели несферич. ядра, впервые предложенной амер. физиком Дж. Рейнуотером (1950) и развитой в работах дат. физика О. Бора и амер. физика Б. Моттельсона. Согласно этой модели, ядро представляет собой эллипсоид вращения. Его большая (a1) и малая (а2) полуоси выражаются через параметр деформации b ядра след. образом: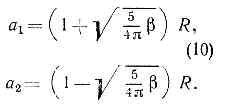 . Электрич. квадрупольный момент несферич. ядра также выражается через b. Параметры b, определённые из данных по квадрупольным моментам (не только статическим, но и динамическим, т. е. по вероятности испускания возбуждённым ядром электрич. квадрупольного g-излучения), оказываются =0,1, но варьируются в широких пределах (у нек-рых ядер редкоземельных элементов b=0,5). От b зависит также момент инерции J ядра. Эксперим. значения J значительно меньше моментов инерции тв. эллипсоида вращения относительно оси, перпендикулярной оси симметрии. Нет также уровней, соответствующих вращению эллипсоида вокруг оси симметрии. Эти обстоятельства исключают возможность буквально отождествить вращение несферич. ядра с квант. вращением симметрич. твердотельного волчка. Принимается схема, аналогичная квантованию движения двухатомной молекулы с идентичными бесспиновыми ядрами: вращат. момент ядер такой молекулы относительно её центра инерции всегда перпендикулярен линии, соединяющей ядра. Из-за свойств симметрии волновой функции относительно перестановки ядер, допустимы только чётные значения момента вращения (0, 2, 4 и т. д.), что соответствует значениям J для ротац. состояний несферич. ядер с чётными А и Z. Для ядер с небольшими b наблюдаемые значения J близки к моменту инерции той части эллипсоида вращения, к-рая находится вне вписанного шара. Такой момент инерции могли бы иметь идеальный газ, помещённый в сосуд в форме эллипсоида вращения, или (что то же самое) ч-цы, движущиеся независимо друг от друга в несферич. эллипсоидальной потенц. яме. С ростом b момент инерции ядра в такой модели растёт, быстро достигая значения тв. эллипсоида. Это противоречит опытным данным, согласно к-рым рост J с увеличением b происходит значительно медленнее, так что для реальных ядер значения J лежат между моментами инерции части эллипсоида, находящегося вне вписанного в него шара и тв. эллипсоида вращения. Противоречие устраняется учётом вз-ствия между ч-цами, движущимися в потенц. яме. При этом, как оказывается, гл. роль играют парные корреляции «сверхтекучего типа» (см. ниже).Описанная картина структуры несферич. ядра соответствует обобщению оболочечной модели на случай движения квазичастиц в сферически-несимметричном потенциальном поле (обобщённая модель). При этом несколько изменяется и схема энергетич. состояний и квант. числа, характеризующие индивидуальные «орбиты» ч-ц. В связи с появлением выделенного направления — оси симметрии эллипсоида, сохраняется проекция момента вращения каждой из ч-ц на эту ось. Момент вращения ч-цы j при этом перестаёт быть определённым квант. числом. Практически, однако, для всех ядер смешивание орбит с разными j мало, так что несферичность ядра в движении ч-ц сказывается гл. обр. на появлении дополнит. квант. числа. Для нечётных ядер спин ядра I получается векторным сложением ротац. момента всего ядра как целого и момента вращения «последнего» нечётного нуклона. При этом энергия ротац. уровня зависит не только от I, но и от проекции полного момента вращения К нечётного нуклона на ось симметрии ядра. Разным А" отвечают разные «ротац. полосы». Общая ф-ла, определяющая энергию ?K ротац. уровня нечётного ядра, имеет вид:
. Электрич. квадрупольный момент несферич. ядра также выражается через b. Параметры b, определённые из данных по квадрупольным моментам (не только статическим, но и динамическим, т. е. по вероятности испускания возбуждённым ядром электрич. квадрупольного g-излучения), оказываются =0,1, но варьируются в широких пределах (у нек-рых ядер редкоземельных элементов b=0,5). От b зависит также момент инерции J ядра. Эксперим. значения J значительно меньше моментов инерции тв. эллипсоида вращения относительно оси, перпендикулярной оси симметрии. Нет также уровней, соответствующих вращению эллипсоида вокруг оси симметрии. Эти обстоятельства исключают возможность буквально отождествить вращение несферич. ядра с квант. вращением симметрич. твердотельного волчка. Принимается схема, аналогичная квантованию движения двухатомной молекулы с идентичными бесспиновыми ядрами: вращат. момент ядер такой молекулы относительно её центра инерции всегда перпендикулярен линии, соединяющей ядра. Из-за свойств симметрии волновой функции относительно перестановки ядер, допустимы только чётные значения момента вращения (0, 2, 4 и т. д.), что соответствует значениям J для ротац. состояний несферич. ядер с чётными А и Z. Для ядер с небольшими b наблюдаемые значения J близки к моменту инерции той части эллипсоида вращения, к-рая находится вне вписанного шара. Такой момент инерции могли бы иметь идеальный газ, помещённый в сосуд в форме эллипсоида вращения, или (что то же самое) ч-цы, движущиеся независимо друг от друга в несферич. эллипсоидальной потенц. яме. С ростом b момент инерции ядра в такой модели растёт, быстро достигая значения тв. эллипсоида. Это противоречит опытным данным, согласно к-рым рост J с увеличением b происходит значительно медленнее, так что для реальных ядер значения J лежат между моментами инерции части эллипсоида, находящегося вне вписанного в него шара и тв. эллипсоида вращения. Противоречие устраняется учётом вз-ствия между ч-цами, движущимися в потенц. яме. При этом, как оказывается, гл. роль играют парные корреляции «сверхтекучего типа» (см. ниже).Описанная картина структуры несферич. ядра соответствует обобщению оболочечной модели на случай движения квазичастиц в сферически-несимметричном потенциальном поле (обобщённая модель). При этом несколько изменяется и схема энергетич. состояний и квант. числа, характеризующие индивидуальные «орбиты» ч-ц. В связи с появлением выделенного направления — оси симметрии эллипсоида, сохраняется проекция момента вращения каждой из ч-ц на эту ось. Момент вращения ч-цы j при этом перестаёт быть определённым квант. числом. Практически, однако, для всех ядер смешивание орбит с разными j мало, так что несферичность ядра в движении ч-ц сказывается гл. обр. на появлении дополнит. квант. числа. Для нечётных ядер спин ядра I получается векторным сложением ротац. момента всего ядра как целого и момента вращения «последнего» нечётного нуклона. При этом энергия ротац. уровня зависит не только от I, но и от проекции полного момента вращения К нечётного нуклона на ось симметрии ядра. Разным А" отвечают разные «ротац. полосы». Общая ф-ла, определяющая энергию ?K ротац. уровня нечётного ядра, имеет вид: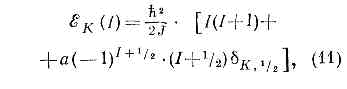 . где dK =0, если К?1/2 и dK,1/2=1 при K=1/2; а — эмпирически подбираемая константа, характеризующая «связь» момента вращения ч-цы и ротац. момента ядра.Моменты инерции для чётных и нечётных по А несферич. ядер одного порядка и таковы, что энергия возбуждения первого ротац. уровня у ядер редкоземельных элементов =100 кэВ (J—10-47 г•см2). Существ. черта ротац. модели несферич. ядер — сочетание медленного вращения всего ядра как целого с быстрым движением отд. нуклонов в несферич. потенц. поле. При этом предполагается, что вращение всего ядра (т. е. несферич. потенц. ямы) происходит достаточно медленно по сравнению со скоростью движения нуклонов. Более точно это означает, что расстояние между соседними ротац. уровнями должно быть мало по сравнению с расстояниями между уровнями энергии нуклонов в потенц. яме. Т. к. адиабатич. приближение для описания энергетич. спектра нек-рых несферич. ядер оказывается недостаточным, то вводятся неадиабатич. поправки (напр., на кориолисовы силы и др.), что приводит к увеличению числа параметров, определяемых из сравнения теории с опытом.Данные о ротац. спектрах несферич. ядер многочисленны. У нек-рых ядер известно неск. ротац. полос (напр., у ядра 235U 9 полос, причём отд. ротац. полосы «прослежены» вплоть до I=25/2 и более). Есть попытки интерпретировать нек-рые лёгкие ядра как несферические (напр., 24Mg). Моменты инерции таких ядер оказываются примерно в 10 раз меньше, чем у тяжёлых. Ротац. модель несферич. ядер позволяет описать ряд существ. свойств большой группы ядер. Вместе с тем эта модель не явл. последоват. теорией, выведенной из «первых принципов». Её исходные положения постулированы в соответствии с эмпирич. данными о ядрах. В рамках этой модели не объяснён и сам факт возникновения ротац. спектра (вращения ядра как целого).Сверхтекучесть ядерного вещества- следствие «спаривания» нуклонов аналогично спариванию эл-нов в сверхпроводниках (см. СВЕРХПРОВОДИМОСТЬ). В безграничном ядре (ядерной материи) в единую «ч-цу» (куперовскую пару) объединялись бы нуклоны с равными, но противоположными по знаку импульсами и проекциями спина. В реальных ядрах предполагается спаривание нуклонов с одними и теми же значениями квант. чисел (j, l) и с противоположными проекциями т полного момента вращения нуклона. Физ. причина спаривания — притягательное вз-ствие ч-ц, движущихся по индивидуальным «орбитам» оболочечной модели. Впервые на возможность сверхтекучести яд. материи указал Н. Н. Боголюбов (1958). Одним из проявлений сверхтекучести яд. материи должно быть наличие энергетич. щели между сверхтекучим и нормальным состояниями в-ва. Величина этой щели определяется энергией связи куперовской пары (энергией спаривания), к-рая для яд. материи (насколько можно судить по разности энергий связи чётных и нечётных ядер) должна составлять примерно 1—2 МэВ. В реальных ядрах наличие энергетич. щели с определённостью установить трудно, т. к. спектр яд. уровней дискретен и расстояние между оболочечными уровнями сравнимо с величиной щели.Наиболее яркое указание на сверхтекучесть яд. в-ва — отличие моментов инерции сильно несферич. ядер от момента тв. эллипсоида. Теория сверхтекучести яд. в-ва удовлетворительно объясняет как величины моментов инерции, так и их зависимость от параметра деформации (5. Теория предсказывает также скачкообразное возрастание J в данной вращат. полосе при нек-ром критическом (достаточно большом) спине ядра I. Это явление, аналогичное разрушению сверхпроводимости достаточно сильным магн. полем, пока отчётливо не наблюдалось. Сверхтекучесть яд. в-ва заметно сказывается на ряде др. свойств ядра: на вероятностях эл.-магн. переходов, на положениях оболочечных уровней и т. п. В целом сверхтекучесть яд. в-ва выражена в реальных ядрах не так ярко, как сверхпроводимость металлов или сверхтекучесть жидкого гелия при низких темп-рах. Причина этого — ограниченность размеров ядер, сравнимых с размером куперовской пары. Менее надёжны и выводы теории сверхтекучести ядер. Гл. препятствием теории и здесь явл. то обстоятельство, что вз-ствие между яд. ч-цами не может считаться слабым (в отличие, напр., от спаривательного вз-ствия эл-нов в металле). Поэтому наряду с парными корреляциями следовало бы учитывать и корреляции большого числа ч-ц (напр., четырёх). Описанные яд. модели явл. основными, охватывающими гл. свойства большинства ядер. Они, однако, не достаточны для описания всех наблюдаемых свойств осн. и возбуждённых состояний ядер. Так, в частности, для объяснения спектра коллективных возбуждений сферич. ядер привлекается модель поверхностных и квадрупольных колебаний жидкой капли, с к-рой отождествляется ядро (вибрационная модель). Для объяснения свойств нек-рых ядер используются представления о «кластерной» структуре ядра. Напр., предполагается, что ядро Li значит. часть времени проводит в виде дейтрона и a-частицы, вращающихся относительно центра масс ядра. Все яд. модели играют роль б. или м. вероятных рабочих гипотез. Последовательное же объяснение наиболее важных свойств ядер на прочной основе общих физ. принципов и данных о вз-ствии нуклонов остаётся пока одной из нерешённых фундаментальных проблем современной яд. физики.
. где dK =0, если К?1/2 и dK,1/2=1 при K=1/2; а — эмпирически подбираемая константа, характеризующая «связь» момента вращения ч-цы и ротац. момента ядра.Моменты инерции для чётных и нечётных по А несферич. ядер одного порядка и таковы, что энергия возбуждения первого ротац. уровня у ядер редкоземельных элементов =100 кэВ (J—10-47 г•см2). Существ. черта ротац. модели несферич. ядер — сочетание медленного вращения всего ядра как целого с быстрым движением отд. нуклонов в несферич. потенц. поле. При этом предполагается, что вращение всего ядра (т. е. несферич. потенц. ямы) происходит достаточно медленно по сравнению со скоростью движения нуклонов. Более точно это означает, что расстояние между соседними ротац. уровнями должно быть мало по сравнению с расстояниями между уровнями энергии нуклонов в потенц. яме. Т. к. адиабатич. приближение для описания энергетич. спектра нек-рых несферич. ядер оказывается недостаточным, то вводятся неадиабатич. поправки (напр., на кориолисовы силы и др.), что приводит к увеличению числа параметров, определяемых из сравнения теории с опытом.Данные о ротац. спектрах несферич. ядер многочисленны. У нек-рых ядер известно неск. ротац. полос (напр., у ядра 235U 9 полос, причём отд. ротац. полосы «прослежены» вплоть до I=25/2 и более). Есть попытки интерпретировать нек-рые лёгкие ядра как несферические (напр., 24Mg). Моменты инерции таких ядер оказываются примерно в 10 раз меньше, чем у тяжёлых. Ротац. модель несферич. ядер позволяет описать ряд существ. свойств большой группы ядер. Вместе с тем эта модель не явл. последоват. теорией, выведенной из «первых принципов». Её исходные положения постулированы в соответствии с эмпирич. данными о ядрах. В рамках этой модели не объяснён и сам факт возникновения ротац. спектра (вращения ядра как целого).Сверхтекучесть ядерного вещества- следствие «спаривания» нуклонов аналогично спариванию эл-нов в сверхпроводниках (см. СВЕРХПРОВОДИМОСТЬ). В безграничном ядре (ядерной материи) в единую «ч-цу» (куперовскую пару) объединялись бы нуклоны с равными, но противоположными по знаку импульсами и проекциями спина. В реальных ядрах предполагается спаривание нуклонов с одними и теми же значениями квант. чисел (j, l) и с противоположными проекциями т полного момента вращения нуклона. Физ. причина спаривания — притягательное вз-ствие ч-ц, движущихся по индивидуальным «орбитам» оболочечной модели. Впервые на возможность сверхтекучести яд. материи указал Н. Н. Боголюбов (1958). Одним из проявлений сверхтекучести яд. материи должно быть наличие энергетич. щели между сверхтекучим и нормальным состояниями в-ва. Величина этой щели определяется энергией связи куперовской пары (энергией спаривания), к-рая для яд. материи (насколько можно судить по разности энергий связи чётных и нечётных ядер) должна составлять примерно 1—2 МэВ. В реальных ядрах наличие энергетич. щели с определённостью установить трудно, т. к. спектр яд. уровней дискретен и расстояние между оболочечными уровнями сравнимо с величиной щели.Наиболее яркое указание на сверхтекучесть яд. в-ва — отличие моментов инерции сильно несферич. ядер от момента тв. эллипсоида. Теория сверхтекучести яд. в-ва удовлетворительно объясняет как величины моментов инерции, так и их зависимость от параметра деформации (5. Теория предсказывает также скачкообразное возрастание J в данной вращат. полосе при нек-ром критическом (достаточно большом) спине ядра I. Это явление, аналогичное разрушению сверхпроводимости достаточно сильным магн. полем, пока отчётливо не наблюдалось. Сверхтекучесть яд. в-ва заметно сказывается на ряде др. свойств ядра: на вероятностях эл.-магн. переходов, на положениях оболочечных уровней и т. п. В целом сверхтекучесть яд. в-ва выражена в реальных ядрах не так ярко, как сверхпроводимость металлов или сверхтекучесть жидкого гелия при низких темп-рах. Причина этого — ограниченность размеров ядер, сравнимых с размером куперовской пары. Менее надёжны и выводы теории сверхтекучести ядер. Гл. препятствием теории и здесь явл. то обстоятельство, что вз-ствие между яд. ч-цами не может считаться слабым (в отличие, напр., от спаривательного вз-ствия эл-нов в металле). Поэтому наряду с парными корреляциями следовало бы учитывать и корреляции большого числа ч-ц (напр., четырёх). Описанные яд. модели явл. основными, охватывающими гл. свойства большинства ядер. Они, однако, не достаточны для описания всех наблюдаемых свойств осн. и возбуждённых состояний ядер. Так, в частности, для объяснения спектра коллективных возбуждений сферич. ядер привлекается модель поверхностных и квадрупольных колебаний жидкой капли, с к-рой отождествляется ядро (вибрационная модель). Для объяснения свойств нек-рых ядер используются представления о «кластерной» структуре ядра. Напр., предполагается, что ядро Li значит. часть времени проводит в виде дейтрона и a-частицы, вращающихся относительно центра масс ядра. Все яд. модели играют роль б. или м. вероятных рабочих гипотез. Последовательное же объяснение наиболее важных свойств ядер на прочной основе общих физ. принципов и данных о вз-ствии нуклонов остаётся пока одной из нерешённых фундаментальных проблем современной яд. физики.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ЯДРО АТОМНОЕ
-
- центральная массивная часть атома, состоящая из протонов и нейтронов (нуклонов). В Я. а. сосредоточена почти вся масса атома (более 99,95%). Размеры ядер порядка 10-13 -10-12 см. Ядра имеют положит. электрич. заряд, кратный абс. величине заряда электрона е: Q = Ze. Целое число Z совпадает с порядковым номером элемента в периодической системе элементов. Я. а. было открыто Э. Резерфордом (Е. Rutherford) в 1911 в опытах по рассеянию a-частиц при прохождении их через вещество.
Состав ядра. Вскоре после открытия нейтрона Дж. Чед-виком (J. Chadwick, 1932), Д. Д. Иваненко и В. Гёйзенбер-гом (W. Heisenberg) независимо было высказано фундам. предположение о том, что Я. а. состоит из протонов (р) и нейтронов (n). Общее число нуклонов в Я. а. наз. м а сс о в ы м ч и с л о м A, число протонов в ядре равно заряду ядра Z, число нейтронов N = A - Z. Ядра с одинаковыми зарядами Z и разным числом нейтронов наз. и з о т о п ам и, ядра с разными Z и одинаковыми N- и з о т о н а м и, ядра с одинаковыми А и разными Z и N- и з о б а р а м и. По совр. представлениям, протон и нейтрон состоят из кварков и глюонов и Я. а.- сложная система из большого кол-ва кварков, глюонных и мезонных полей, взаимодействующих друг с другом. Последовательное описание Я. а. должно достигаться в рамках квантовой хромодинамики. Однако в силу своей сложности эта задача ещё не решена.
Составная природа нуклонов проявляется лишь в столкновениях с большой передачей импульса и энергии. При небольших энергиях возбуждения такие столкновения в ядре редки. Поэтому при описании Я. а. и ядерных реакций, происходящих при не слишком больших энергиях (<= 1 ГэВ на нуклон), в первом приближении можно считать, что ядра состоят из вполне определённого числа нуклонов, движущихся с нерелятивистскими скоростями (u2/c2~0,l). Кварки "заперты" каждый в своём нуклоне. Нуклоны не теряют своей индивидуальности и обладают примерно такими же свойствами, как и в свободном состоянии (за нек-рыми исключениями, см. ниже). Протонно-нейтронная картина строения Я. а. является приближённой и нарушается при высоких энергиях возбуждения и в процессах с большой передачей импульса и энергии.
В обычных условиях отклонения от протонно-нейтрон-ной модели, связанные с составной природой нуклонов и кварк-глюонной структурой Я. а., невелики и заключаются в следующем. 1) В результате взаимодействия между нуклонами последние могут существовать в Я. а. не только в основном, но и в возбуждённых состояниях, наз. н у к л о н н ы м и и з о б а р а м и. Низшим из них по энергии является т. н. D-изобара (см. Резонансы). Часть времени (~ 1%) нуклоны в ядре могут пребывать в виде нуклонных изобар. 2) Запирание кварков в нуклонах не является абсолютным, в ядре могут на короткое время образовываться сгустки кварк-глюонной материи ( флуктоны), состоящие из 6, 9 и т. д. кварков (см. Кварк-глюонная плазма).3) Свойства нуклонов, связанных в ядре, могут отличаться от свойств свободных нуклонов. Как показывают эксперименты по глубоко неупругому рассеянию (см. Глубоко неупругие процессы) лептонов на ядрах, структурные ф-ции нуклонов в ядре, характеризующие распределение кварков по импульсам в нуклоне, отличаются от структурных ф-ций свободных нуклонов (эффект ЕМС - Европейской Мюонной Коллаборации, ЦЕРН, 1982). Одно из возможных объяснений эффекта ЕМС основано на гипотезе об увеличении радиуса нуклона в ядре по сравнению со свободным нуклоном. 4) В ядрах периодически на время 10-23-10-24 с появляются (виртуальные) мезоны, в т. ч. пи-мезоны. Исследование ненуклонных степеней свободы ядра - осн. предмет совр. исследований в релятивистской ядерной физике.
Ядерные силы. Нуклоны являются адронами, т. е. принадлежат к числу частиц, испытывающих сильное взаимодействие. Взаимодействие между нуклонами, удерживающее их в ядре, т. е. ядерные силы, возникает в результате взаимодействия между составными частями (кварки, глю-оны), к-рые образуют нуклоны. Теория ядерных сил на основе кварковых представлений находится в стадии становления и пока не завершена.
Традиционная мезонная теория ядерных сил основана на идее, предложенной в 1935 X. Юкавой (Н. Yukawa). Согласно мезонной теории, взаимодействие между нуклонами осуществляется путём обмена мезонами. Ядерные силы характеризуются радиусом действия; он определяется ком-птоновской длиной волны мезонов, к-рыми обмениваются нуклоны,
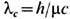 , где m - масса мезона. Наиб. радиус действия имеют силы притяжения, обусловленные обменом я-мезонами. Для них l с=1,41 Фм (1 Фм=10-13 см). Это соответствует расстоянию между нуклонами в ядрах. Обмен более тяжёлыми мезонами (r, w и др.) оказывает влияние на взаимодействие между нуклонами на меньших расстояниях, вызывая, в частности, отталкивание между ними на расстояниях <=0,4 Фм.
, где m - масса мезона. Наиб. радиус действия имеют силы притяжения, обусловленные обменом я-мезонами. Для них l с=1,41 Фм (1 Фм=10-13 см). Это соответствует расстоянию между нуклонами в ядрах. Обмен более тяжёлыми мезонами (r, w и др.) оказывает влияние на взаимодействие между нуклонами на меньших расстояниях, вызывая, в частности, отталкивание между ними на расстояниях <=0,4 Фм.
Размеры ядер зависят от числа нуклонов в ядре и изменяются в пределах от 10-13 до 10-12 см. Эксперим. данные показывают, что ср. плотность нуклонов (число нуклонов в единице объёма) почти одинакова во всех ядрах с А>=20. Это означает, что объём ядра пропорционален А, а его радиус R пропорционален А1/3:

где постоянная а близка к радиусу действия ядерных сил. Различают зарядовый радиус ядра, т. е. ср. радиус распределения протонов в ядре, и радиус распределения ядерного вещества (радиус распределения нуклонов независимо от их сорта). Первый измеряется в экспериментах с электромагнитным взаимодействием (рассеяние электронов высоких энергий на ядрах, исследование уровней мюонных атомов), что даёт значение а =1,12 Фм; второй - в ядерных реакциях с участием адронов (рассеяние нуклонов, a-частиц, взаимодействие p- и К-мезонов с ядрами и др.). При этом получают несколько большее значение а =1,2-1,4 Фм. Ср. плотность ядерного вещества очень велика и составляет ~ 1014 г/см 3.
Эксперименты по рассеянию быстрых электронов на ядрах позволили не только определить ср. размеры ядра, но и детально исследовать распределение заряда r(r )в ядре. Эксперим. результаты лучше согласуются не с однородным распределением заряда в ядре, а с т. н. фермиев-ским распределением:
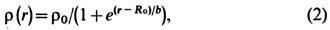
где R0 = 1,1 А1/3 Фм. Это распределение показывает, что плотность заряда почти постоянна во внутр. области (r<R0 )тяжёлого или ср. ядра и экспоненциально спадает за её пределами. Параметр b = 0,5 Фм характеризует "размытость" поверхности ядра; он почти одинаков для всех ядер и означает, что "толщина" ядерной поверхности (интервал, на к-ром плотность заряда убывает от 90% до 10% значения r0 = 0,17 нуклон/Фм 3) составляет 2,2 Фм. Ф-лы (1,2) описывают зависимость радиуса ядра R и плотности заряда r(r )от А в среднем и не учитывают индивидуальных особенностей строения ядер. Последние могут привести к нерегулярностям в изменении R. В частности, из измерений изотопических сдвигов энергий атомных уровней следует, что иногда радиус ядра может даже уменьшаться при добавлении двух нейтронов (напр., радиус ядра 48 Са меньше радиуса 46 Са). Измерение изотопич. сдвигов уровней атомов и мезоатомов дало возможность оценить изменение радиуса ядра в возбуждённом состоянии. Как правило, по мере возбуждения ядра его радиус увеличивается, но незначительно (доли %). Имеющиеся данные свидетельствуют о том, что распределения протонов и нейтронов в ядре практически одинаковы. Но в тяжёлых ядрах из-за больших кулоновских сил и связанного с ними избытка нейтронов радиус распределения нейтронов может немного превышать радиус распределения заряда (н е й т р о н н о е г а л о). Подобное гало может возникать также в лёгких ядрах, перегруженных нейтронами (11Li).
Энергия связи и масса ядра. Энергией связи ядра
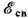 наз. энергия, к-рую необходимо затратить, чтобы расщепить ядро на отд. нуклоны. Она равна умноженной на с2 разности суммарной массы всех нуклонов, входящих в состав ядра, и массы М самого ядра:
наз. энергия, к-рую необходимо затратить, чтобы расщепить ядро на отд. нуклоны. Она равна умноженной на с2 разности суммарной массы всех нуклонов, входящих в состав ядра, и массы М самого ядра:
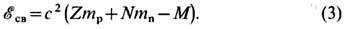
Здесь т р, тn - массы протона и нейтрона. Энергия связи ядра примерно пропорц. числу нуклонов в ядре, а уд. энергия связи
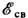 /А почти постоянна (для большинства ядер
/А почти постоянна (для большинства ядер 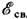 /A~6-8 МэВ). Это свойство, называемое н а с ыщ е н и е м я д е р н ы х с и л, означает, что нуклон в ядре эффективно взаимодействует не со всеми нуклонами ядра, а только с нек-рым ограниченным их числом (в противном случае уд. энергия связи была бы пропорц. А).
/A~6-8 МэВ). Это свойство, называемое н а с ыщ е н и е м я д е р н ы х с и л, означает, что нуклон в ядре эффективно взаимодействует не со всеми нуклонами ядра, а только с нек-рым ограниченным их числом (в противном случае уд. энергия связи была бы пропорц. А).
Постоянство плотности и уд. энергии связи ядра сближает свойства ядра со свойствами жидкости. Это сходство легло в основу модели ядра как жидкой капли ( капельная модель ядра), исходя из к-рой К. Ф. фон Вайцзеккер (С. F. von Weizsacker) в 1935 предложил полуэмпирич. ф-лу ( Вайцзеккера формула )для энергии связи ядра:
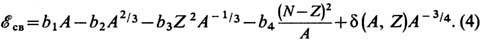
Здесь первый член описывает объёмную энергию "капли", второй - характеризует ослабление связи для нуклонов, находящихся на поверхности ядра, третий член описывает вклад кулоновской энергии капли радиусом R~A1/3 и с зарядом Z. Четвёртый член (т. н. э н е р г и я с и м м е т р и и) не имеет классич. аналога и отражает тот факт, что притяжение между нуклонами разного сорта в ср. сильнее, чем для одинаковых нуклонов. Это вместе с Паули принципом делает энергетически невыгодным значит. отклонение N от Z. Пятый член наз. э н е р г и е й с п а р и в а н и я:

Он воспроизводит опытный факт, что четно-чётные ядра (Z и N чётные) связаны сильнее, чем соседние четно-нечётные, а последние, в свою очередь, более устойчивы, чем нечётно-нечётные ядра.
Совр. значения параметров ф-лы Вайцзеккера: b1 =15,75 МэВ, b2 = 17,8 МэВ, b3 = 0,71 МэВ, b4 = 23,7 МэВ. Ф-ла (4) в ср. хорошо описывает энергии связи ядер, ограничивает значением Z2/A ~46 область существования ядер, устойчивых по отношению к делению. Однако она не учитывает индивидуальных особенностей оболочечной структуры ядра. Эти эффекты можно учесть методом оболочечной поправки Струтинского, предсказывающим возможность существования т. н. о с т р о в о в с т а б и л ьн о с т и сверхтяжёлых ядер при Z~114 (см. Трансурановые элементы).
Квантовые характеристики ядерных уровней. Я. а. при энергиях ниже порога распада (с испусканием нуклона, a-частицы и т. п.) может находиться только в дискретных состояниях с определ. энергией, характеризующихся набором квантовых чисел, задающих значения сохраняющихся величин (интегралов движения) в этих состояниях. Выше порога распада ядра дискретные состояния становятся нестационарными и проявляются в ядерных реакциях как резонансы конечной ширины.
Наиб. важными характеристиками ядерных состояний являются спин ядра (или момент кол-ва движения, называемый также у г л о в ы м м о м е н т о м я д р а) I и чётность p = + 1. Спин / измеряется в единицах
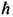 и принимает полуцелые значения (I= 1/2,3/2, ...) У нечётных ядер и целочисленные значения (I=0, 1, 2, ....) у чётных ядер. Чётность pуказывает на симметрию волновой ф-ции y ядерного состояния относительно зеркального отражения пространства Р (см. Пространственная инверсия): Рy = py. В связи с этим для ядерных состояний указывают объединённую характеристику Ip. Эмпирически установлено, что осн. состояния четно-чётных ядер имеют характеристику 0+ . Спины и чётности нечётных ядер, как правило, объясняются моделью оболочек (см. ниже). Строго говоря, чётность не является точным квантовым числом, поскольку она не сохраняется при слабом взаимодействии. За счёт сил электрослабого взаимодействия между нуклонами происходит смешивание состояний с одним и тем же спином I и противоположными чётностями. Однако вследствие малости сил, нарушающих чётность, указанное смешивание мало и им можно пренебречь при рассмотрении спектров ядерных уровней, разнообразных ядерных реакций и переходов, за исключением процессов, направленных специально на изучение явления несохранения чётности в ядрах.
и принимает полуцелые значения (I= 1/2,3/2, ...) У нечётных ядер и целочисленные значения (I=0, 1, 2, ....) у чётных ядер. Чётность pуказывает на симметрию волновой ф-ции y ядерного состояния относительно зеркального отражения пространства Р (см. Пространственная инверсия): Рy = py. В связи с этим для ядерных состояний указывают объединённую характеристику Ip. Эмпирически установлено, что осн. состояния четно-чётных ядер имеют характеристику 0+ . Спины и чётности нечётных ядер, как правило, объясняются моделью оболочек (см. ниже). Строго говоря, чётность не является точным квантовым числом, поскольку она не сохраняется при слабом взаимодействии. За счёт сил электрослабого взаимодействия между нуклонами происходит смешивание состояний с одним и тем же спином I и противоположными чётностями. Однако вследствие малости сил, нарушающих чётность, указанное смешивание мало и им можно пренебречь при рассмотрении спектров ядерных уровней, разнообразных ядерных реакций и переходов, за исключением процессов, направленных специально на изучение явления несохранения чётности в ядрах.
Ещё одной важной, хотя и приближённой ядерной характеристикой является изотопический спин (или изобарический спин) Т, к-рый складывается из изоспинов отд. нуклонов по тем же правилам, что и обычный спин. Сохранение этой величины связано с изотопической инвариантностью ядерных сил, к-рая состоит в том, что ядерные взаимодействия между двумя нуклонами в одинаковых пространств. и спиновых состояниях не зависят от сорта нуклонов, т. е. одинаковы в парах рр, рп и пп. Изотопич. спин (изоспин) может принимать значения T>=(N-Z)/2, целые для чётных ядер и полуцелые для нечётных. Подобно обычному спину, он имеет также фиксированную проекцию на одну из осей формального изоспинов. пространства TZ = (A -2Z)/2. Она связана с зарядом ядра и поэтому является строго сохраняющейся величиной во всех ядерных состояниях. В отличие от этого, изоспин Т является приближённым квантовым числом. Нарушение изоспина (т. е. смешивание компонент с разл. значениями Т в волновой ф-ции ядерного состояния) обусловлено различием масс протона и нейтрона, а также кулоновским взаимодействием между протонами. В лёгких ядрах с Z<=20 эти эффекты малы и изоспин Т является достаточно точным квантовым числом. В результате ядерные состояния можно характеризовать квантовыми числами Т и TZ, a состояния с одинаковыми значениями Ip, Т в соседних ядрах-изобарах объединить в и з о т о п и ч. м у л ь т и п л е т ы. Поскольку проекция изоепина принимает значения TZ=T, Т-1,...., - T, то в изотопич. мульти-плет входит 2 Т+1 уровней.
Опытным путём установлено, что энергия возбуждения ядерного состояния тем выше, чем больше изоспин. Поэтому в осн. состоянии ядра Т= TZ и у четно-чётных ядер с Z=N T=0. Ядра с T=1/2 и TZ = b1/2 образуют изодуб-лет (напр., 3 Н - 3 Не). Примером изотриплета могут служить осн. состояние 0+ ( Т=1, Т Z=1) ядра 6 Не, возбуждённое состояние 0+ ( Т=1, TZ =0)ядра 6Li. (энергия возбуждения 3,56 МэВ) и осн. состояние ядра 6 Ве ( Т=1, TZ=-1). В ядерной физике принято приписывать нуклону изоспин Т=1/2 и значения Т Z=1/2. нейтрону, TZ=-1/2 протону, в отличие от физики элементарных частиц, где используются противоположные знаки проекций изоcпина нуклона. Это сделано из соображений удобства, чтобы значения TZ были положительны для стабильных ядер, у к-рых N> Z.
Состояния ядер, входящих в состав одного изотопич. мультиплета, наз. аналоговыми состояниями. Вследствие изотопич, инвариантности ядерных сил структура (чисто ядерная) этих состояний одинакова, а все отличия в их свойствах обусловлены эл.-магн. взаимодействием. Напр., энергии связи аналоговых состояний одинаковы с точностью до различия кулоновских энергий в ядрах данного мультиплета. С увеличением Z возрастает роль кулонов-ского взаимодействия. Поэтому в тяжёлых ядрах точность изоепина как квантового числа уменьшается. Тем не менее следы изоспиновой симметрии проявляются в том, что в разл. ядерных реакциях наблюдаются открытые в 1961 состояния, нестабильные по отношению к испусканию нуклона, к-рые являются аналогами основного или низших стабильных возбуждённых состояний соседнего ядра с меньшим Z (а н а л о г о в ы е р е з о н а н с ы). Напр., при рассеянии протонов на стабильном ядре А счислами нейтронов и протонов N и Z (T0 = TZ = (N-Z)/2)наблюдаются резонансы, отвечающие образованию составного ядра А+1(Z+l, N )ввозбуждённом состоянии с квантовыми числами T=T0 +1/2, TZ=T0 -1/2, входящем в тот же изотопич. мультиплет, что и осн. состояние соседнего ядра А +1(N+1, Z), T=TZ=T0 +1/2. Однако эксперименты показали, что аналоговые резонансы имеют тонкую структуру, к-рая свидетельствует о том, что имеет место смешивание аналогового состояния, характеризуемого изоспином T0 +1/2 c др. возбуждёнными состояниями составного ядра, отвечающими изоспину Т=Т0 -1/2.
Электрические и магнитные моменты ядер. В каждом из возможных состояний Я. а. имеет определ. значения магн. дипольного момента и квадрупольного электрического момента (см. Квадрупольный момент ядра). Статич. магн. момент может быть отличен от 0 только в том случае, когда спин ядерного состояния I
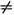 0, а статич. квадруполь-ный момент может иметь ненулевое значение лишь при I> 1/2. Ядерное состояние с определ. чётностью не может иметь отличного от нуля электрич. дипольного момента ( Е1), а также др. электрич. моментов Elнечётной муль-типольности l и статич. магн. моментов Ml чётной муль-типольности l. Существование ненулевого электрич. дипольного момента E1 запрещено также инвариантностью относительно обращения времени (T -инвариантность). Поскольку эффекты несохранения чётности и нарушения T -инвариантности очень малы, то дипольные электрич. моменты ядер или равны 0, или очень малы и пока недоступны для измерения.
0, а статич. квадруполь-ный момент может иметь ненулевое значение лишь при I> 1/2. Ядерное состояние с определ. чётностью не может иметь отличного от нуля электрич. дипольного момента ( Е1), а также др. электрич. моментов Elнечётной муль-типольности l и статич. магн. моментов Ml чётной муль-типольности l. Существование ненулевого электрич. дипольного момента E1 запрещено также инвариантностью относительно обращения времени (T -инвариантность). Поскольку эффекты несохранения чётности и нарушения T -инвариантности очень малы, то дипольные электрич. моменты ядер или равны 0, или очень малы и пока недоступны для измерения.
Магн. моменты ядер (M1) имеют порядок величины ядерного магнетона. Электрич. квадрупольные моменты eQ изменяются от е•10-27 см 2 в нек-рых лёгких ядрах до е•10-24 см 2 в тяжёлых деформированных ядрах. Систематическая информация о магн. и квадрупольных моментах имеется только для осн. состояний ядер. Они могут быть измерены радиоспектроскопич. методами (см. Ядерный магнитный резонанс). Спец. методами (м е т о д в о з м ущ ё н н ы х у г л о в ы х к о р р е л я ц и й) можно измерять также статич. магн. и квадрупольные моменты возбуждённых состояний ядер. Данные по магн. и квадруполь-ным моментам ядер содержат важную информацию о структуре и форме ядер и используются для построения и проверки ядерных моделей. Есть нек-рые данные о высших мультипольных моментах ядер (напр., гексадека-польных - Е4).
Структура и модели ядер
Я. а. представляет собою квантовую систему мн. тел, сильно взаимодействующих друг с другом. Теоретич. описание свойств такой системы (спектров энергетич. уровней, распадов, ядерных реакций и квантовых переходов) является трудной задачей. Число нуклонов А в ядре не столь велико, чтобы можно было без оговорок использовать методы статистич. механики (см. Гиббса распределения), успешно применяемой в физике конденсир. сред (жидкости, твёрдые тела). В то же время точное решение в квантовой механике возможно лишь для задачи двух тел (дейтрон). Успехи, достигнутые в решении задачи 3-4 тел гл. обр. с помощью ур-ний Фаддеева и Фаддеева-Якубовского, позволяют получать строгие количеств. результаты лишь для самых лёгких ядер 3 Н, 3 Не, 4 Не. Ситуация осложняется недостаточной определённостью наших знаний о ядерных силах. Наконец, установление составной природы нуклонов превращает систему А нуклонов в систему, по крайней мере, 3 А кварков, что ещё более усложняет задачу описания структуры и свойств ядер. Последовательное решение этой задачи может быть достигнуто только в рамках (непертурбативной) квантовой хромодинамики, но она ещё далека от разрешения.
Понимание структуры ядра основано на использовании разл. ядерных моделей, каждая из к-рых имеет целью описание определ. совокупности ядерных свойств и характеристик. Нек-рые модели, на первый взгляд, являются взаимоисключающими. Поэтому важными являются микро-скопич. подходы в теории ядра, позволяющие установить пределы применимости разл. моделей, степень их совместимости друг с другом, а также оценить или вычислить, исходя из первых принципов, значения параметров, к-рые используются в моделях как феноменологические и извлекаются из данных эксперимента.
Оболочечная модель ядра предполагает, что в результате взаимодействия нуклонов друг с другом в ядре формируется общее среднее (самосогласованное) поле, описываемое оболочечным потенциалом Vo6(r), в к-ром нуклоны движутся как независимые (в первом приближении) частицы. Каждый из нуклонов заполняет одну из орбит, характеризуемую орбитальным моментом l (в случае сферически симметричного ср. поля), полным угл. моментом j=l+ 1/2 и чётностью p = (- 1)l. Энергия нуклона на орбите lj не зависит от проекции т полного момента нуклона j (-j<=m<=j). Поэтому в соответствии с принципом Паули на каждом уровне с энергией
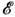 (nlj )может находиться 2j+1 нуклонов одного сорта, образующих протонную (или нейтронную) подоболочку (nlj), где п=1,2,...- гл. квантовое число (радиальное).
(nlj )может находиться 2j+1 нуклонов одного сорта, образующих протонную (или нейтронную) подоболочку (nlj), где п=1,2,...- гл. квантовое число (радиальное).
Неск. близких по энергии подоболочек группируются в оболочки, отделённые друг от друга большими энерге-тич. интервалами. Полный момент I для k нуклонов в оболочке получается путём сложения моментов j отд. нуклонов. В заполненной оболочке моменты всех нуклонов компенсируют друг друга и допустимо только одно значение полного момента I= 0. Подобно атомам благородных газов, обладающих заполненными электронными оболочками, ядра, состоящие из заполненных нуклонных оболочек, также характеризуются особой устойчивостью (большой уд. энергией связи). В основном и низколежащих возбуждённых состояниях ядер низшие одночастичные орбиты заполнены и образуют "инертный" остов ядра, сверх к-рого есть нек-рое число нуклонов в ближайшей незаполненной оболочке. Подобно тому как валентные электроны определяют хим. свойства атомов, спектры низших уровней и их свойства в большинстве ядер определяются "валентными" нуклонами из незаполненных оболочек.
Простейший вариант модели оболочек (одночастичная модель) представляет нечётное ядро как совокупность четно-чётного остова в состоянии 0+ и нечётного нуклона на орбите nlj. Тогда спин нечётного ядра в осн. состоянии равен j, а чётность p = (- 1)l. Систематика спинов и чёт-ностей нечётных ядер позволяет определить последовательность заполнения орбит в ядрах, а также энергии этих орбит. Это дало возможность установить осн. характеристики и форму оболочечного потенциала Vo6(r). В частности, М. Гёпперт-Майер (М. Goeppert-Mayer, США) и И. X. Йенсеном (J. H. Jensen, ФРГ) в 1949-50 была установлена необходимость включения в оболочечный потенциал спин-орбитального взаимодействия Vco(r) (ls). Только при учёте сильного спин-орбитального расщепления одночастичных состояний удаётся объяснить систематику спинов ядер и последовательность заполнения орбит, а также магич. числа протонов или нейтронов, отвечающие заполненным оболочкам (см. Магические ядра). Магич. числа (2, 8, 20, 28, 50, 82, 126) соответствуют после-доват. заполнению нуклонами одного сорта оболочек:
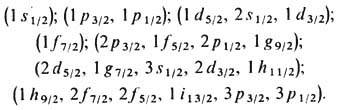
В скобках указана совокупность близких по энергии одно-частичных состояний, образующих одну оболочку. Оболочки отделены друг от друга энергетич. щелью, значительно превышающей расстояние между уровнями в пределах одной оболочки (рис. 1).
Центр. часть оболочечного потенциала представляет собою потенц. яму конечной глубины, форма к-рой повторяет распределение ядерной плотности. Чаще всего в качестве оболочечного потенциала используют т. н. потенциал Саксона - Вудса:
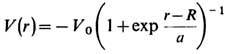
с V0
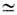 50 МэВ. При описании связанных состояний нуклонов его можно приближённо заменить потенциалом гар-монич. осциллятора или прямоуг. ямой и использовать при описании свойств ядерных состояний волновые ф-ции нуклонов для этих простых оболочечных потенциалов.
50 МэВ. При описании связанных состояний нуклонов его можно приближённо заменить потенциалом гар-монич. осциллятора или прямоуг. ямой и использовать при описании свойств ядерных состояний волновые ф-ции нуклонов для этих простых оболочечных потенциалов.
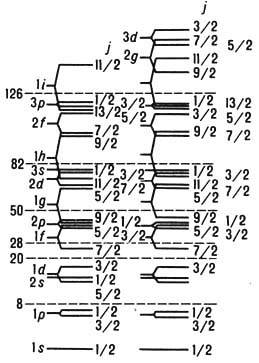
Рис. 1. Схема заполнения ядерных оболочек протонами (слева) и нейтронами (справа). Справа от уровней указаны полные угловые моменты ядра; слева - спектроскопические символы: буква отвечает определённому значению l [l=0 (s),1(p),2(d), 3(f), 4(g), 5(h), 6(i)]; цифра-главное квантовое число. Пунктиром отмечены магические числа заполнения оболочек.
Модель оболочек удовлетворительно описывает магн. моменты нечётных ядер, к-рые, согласно опытным данным, лежат между т. н. линиями Шмидта. Линиями Шмидта наз. зависимости магн. дипольных моментов нуклонов М от угл. момента j при данном l=jb 1/2 (рис. 2). Несколько хуже описываются электрич. квадрупольные моменты ядерных состояний. Последнее связано с тем, что потенциал Vo6(r) предполагался первоначально сферически симметричным.
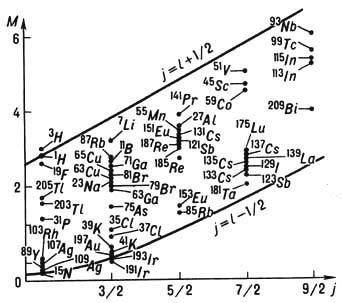
Рис. 2. Линии Шмидта для ядер с нечётным числом протонов Z.
Несферичность ядер. Ротационная модель. Особенно велики квадрупольные моменты Q ядер с I>1/2 в области редких земель (150<A<190) и актинидов ( А>200). Они превышают значения, предсказываемые моделью оболочек со сферич. потенциалом V об, в 10-100 раз. Энергии низших уровней этих ядер удовлетворяют "вращательному закону":

к-рый описывает спектр вращат. уровней жёсткого симметричного волчка с моментом инерции J (см. Вращательное движение ядра). Состояния такого волчка с угл. моментами I=K, K+1, К+2, ... образуют вращат. полосу, характеризуемую определ. значением проекции угл. момента на ось симметрии волчка I3 = К. Исключение составляют полосы с К=0, для к-рых допустимы только чётные или только нечётные значения угл. момента I. В частности, на осн. состояниях четно-чётных ядер базируются вращат. полосы с К=0. и значениями Ip = 0+ , 2+ , 4+, ... Между соседними уровнями вращат. полос имеют местo сильные электрич. квадрупольные ( Е2)g-переходы.
Эти факты послужили основой для построения коллективной модели ядра, предложенной в 50-х гг. Дж. Рейнуотером, О. Бором и Б. Моттельсоном (J. Rainwater, A. Bohr, В. R. Mottelson). Согласно этой модели, ядра в указанных выше областях имеют форму эллипсоида вращения с полуосями
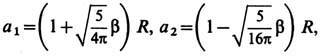
где параметр деформации Р характеризует степень несферичности ядра. Он определяет значения статических ква-друпольных моментов ядер, вероятности эл.-магн. E2-пе-реходов между вращат. уровнями и значения момента инерции ядра (см. Деформированные ядра). Согласно данным эксперимента, величина b у большинства деформированных ядер находится в пределах 0,1-0,3 (нормальная деформация). С помощью ядерных реакций с тяжёлыми ионами обнаружены возбуждённые вращат. состояния у нек-рых ядер (152Dy) с большими угл. моментами I~40-60 ( высокоспиновые состояния ядер), к-рые характеризуются чрезвычайно большой деформацией, когда отношение полуосей ядра а1: а2= 2:1 или 3:2 (супердефор-мир. полосы). Нек-рые деформир. ядра (изотопы Os, Pt) не имеют осевой симметрии. Их низшие уровни представляют собою вращат. состояния асимметричного волчка (модель неаксиального ротатора Давыдова-Филиппова). Масштаб вращат. энергий (
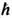 2/2J~= 100 кэВ) в тяжёлых деформир. ядрах таков, что момент инерции ядра в состояниях с нормальной деформацией J~10-27 г . см 2. Он в 2- 3 раза меньше момента инерции твёрдого эллипсоида соответствующей формы. Это означает, что не вся масса ядра участвует во вращат. движении. В супердеформир. полосах момент инерции близок к твердотельному.
2/2J~= 100 кэВ) в тяжёлых деформир. ядрах таков, что момент инерции ядра в состояниях с нормальной деформацией J~10-27 г . см 2. Он в 2- 3 раза меньше момента инерции твёрдого эллипсоида соответствующей формы. Это означает, что не вся масса ядра участвует во вращат. движении. В супердеформир. полосах момент инерции близок к твердотельному.
Внутр. структура деформир. ядер описывается моделью оболочек с деформир. потенциалом Voб (r )(модель Нильс-сона). Изучение зависимости энергии одночастичных орбит нуклонов от деформации в этой модели показывает, что в нек-рых областях периодич. системы элементов ядрам энергетически выгодно быть не сферическими, а деформированными. Величина деформации, предсказываемая теорией, в целом согласуется с экспериментом. На базе колебательных возбуждений деформир. ядра (см. Колебательные возбуждения ядер )возникают новые вращат. полосы (b-полоса с К=0и g-полоса с К=2). Перестройка заполнения одночастичных орбит в деформир. потенциале порождает возбуждённые вращат. полосы. В результате в спектрах ряда ядер можно выделить значит. число вращат. полос (до 9 в ядре 235U). Отд. полосы прослежены до весьма высоких значений угл. момента I~25-30. Значит. деформацию, а также вращат. спектры имеют нек-рые относительно лёгкие ядра (напр., 20Ne, 4Mg). При изменении параметра деформации ядра b меняется структура оболочек. При больших b (a1:a2 =2:1)одночастичные орбиты группируются в оболочки иначе, чем при нормальных деформациях, появляются новые магич. числа. Ядра, близкие к магическим (напр., 152Dy), с такой деформацией относительно устойчивы и могут порождать вращат. полосы. Они были обнаружены экспериментально в виде супердеформир. полос.
Структура вращат. спектров реальных ядер отклоняется от идеального вращат. закона (5)за счёт центробежных эффектов (увеличение момента инерции ядра при возрастании вращат. момента), а также за счёт Кориолиса сил и др. неадиабатич. поправок. Связь движения отд. нуклонов с вращением ядра как целого сказывается на структуре вращат. состояний нечётных ядер уже при небольших значениях b и К, приводя к тому, что их энергии вместо (5) описываются ф-лой
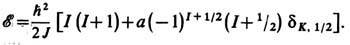
Здесь dK,1/2=0 при К
 1/2 и d К,1/2=1 при К=1/2, константа а -эмпирически подбираемый "параметр развязывания", характеризующий связь угл. момента нуклона и вращат. момента ядра.
1/2 и d К,1/2=1 при К=1/2, константа а -эмпирически подбираемый "параметр развязывания", характеризующий связь угл. момента нуклона и вращат. момента ядра.
Сверхтекучая модель ядра. Парные корреляции сверх-проводящего типа возникают в ядре за счёт т. н. о с т ат о ч н о г о в з а и м о д е й с т в и я между нуклонами, той части реального нуклон-нуклонного взаимодействия, к-рая не включена в самосогласованный потенциал ср. поля V об(r). Эмпирически отмечалась энергетич. выгодность двум нуклонам на орбите nlj образовать пару со скомпен-сир. спинами, т. е. с полным моментом I=0. Такая пара подобна куперовской паре электронов с противоположными импульсами в сверхпроводнике. Притяжение между нуклонами в указанных состояниях вблизи поверхности Ферми обусловливает сверхтекучесть атомных ядер.
Детально сверхтекучая модель ядра разработана независимо С. Т. Беляевым и В. Г. Соловьёвым с помощью методов, аналогичных методам теории сверхпроводимости. Одним из проявлений сверхтекучести ядерного вещества может служить наличие энергетич. щели D между сверхтекучим и нормальным состоянием ядерного вещества. Она определяется энергией разрушения куперовской пары и составляет в тяжёлых ядрах ~ 1 МэВ. Со сверхтекучестью ядерного вещества связано также и отличие моментов инерции ядер от твердотельных значений. Сверхтекучая модель ядра удовлетворительно описывает моменты инерции ядер, изменение параметра деформации ядра b по мере заполнения валентной оболочки нуклонами. Сверхтекучесть ядерного вещества, приводящая к размытию ферми-поверхности, существенным образом сказывается на эл.-магн. переходах, вероятностях реакций однонуклон-ной (срыв, подхват) и двухнуклонной передачи (см. Прямые ядерные реакции).
Сверхтекучая модель предсказывает разрушение парных корреляций в ядре при достаточно больших спинах (I>>1). Это явление, аналогичное разрушению сверхпроводимости сильным магн. полем, проявляется в скачкообразном возрастании момента инерции J в данной вращат. полосе при нек-ром критич. значении спина I кр~60. Отчётливо это пока не обнаружено, однако при изучении высокоспиновых состояний ядер (I<=20-30), возбуждаемых в реакциях с тяжёлыми ионами, наблюдалось немонотонное изменение J при возрастании I (о б р а т н ы й з а г и б). В районе значений спина IB(~12-16) увеличение угл. момента I приводит не к увеличению угл. скорости вращения w, а к её уменьшению вследствие того, что резко увеличивается момент инерции ядра J. Это изменение связано с тем, что вблизи точки IB происходит пересечение основной вращат. полосы ядра ( К=0+ )свозбуждённой полосой, построенной на внутр. состоянии ядра, в к-ром одна из куперовских пар на нейтронной орбите h11/2 разрушается и спины этих двух нуклонов уже не компенсируют друг друга, а оба выстраиваются параллельно вращат. моменту. При этом меняется деформация ядра, увеличивается момент инерции, изменяются магн. характеристики ядра.
Разрушение пары обусловлено силами Кориолиса, эффект к-рых максимален для нуклонов в оболочках с большими моментами нуклонов j. Обнаружено выстраивание протонов на орбите h11/2. и нейтронов на орбите i13/2. Выстраивание двух пар нуклонов приводит ко второму обратному загибу и т. д. Вопрос о характере сверхтекучести ядерного вещества в супердеформир. состояниях находится в стадии исследования.
Другие модели ядра. Наряду с осн. моделями ядра используются более специализир. модели. К л а с т е р н а я м о д е л ь трактует структуру нек-рых ядер как своего рода молекулу, состоящую из a-частиц, дейтронов (d), тритонов(t) и др. Напр., l2C = 3a, 16O = 4a, 6Li = a+d, 7Li = a + t и т. д. (см. Нуклонных ассоциаций модель). Статистическая модель ядра описывает свойства и характеристики высоковозбуждённых состояний ядер, такие, как плотность уровней, темп-ра и т. п.
В м о д е л и в з а и м о д е й с т в у ю щ и х б о з о н о в предполагается, что в низших состояниях четно-чётного ядра нуклоны объединяются в S- и D -пары (с моментами 0 и 2), к-рые приближённо можно трактовать как идеальные s- и d -бозоны. Число этих бозонов равно половине числа валентных нуклонов. В этой модели спектр низших коллективных состояний ядра формируется в результате взаимодействия между бозонами. Более рафинированные варианты данной модели включают в себя s-, d-, g-,.... бозоны, а также сопоставляют разные бозоны протонным и нейтронным парам. Модель взаимодействующих бозонов позволяет описывать наряду с вращат. и колебат. спектрами также спектры более сложной структуры, характерные для ядер, переходных от сферических ядер к деформированным. Обоснование ядерных моделей и более детальные расчёты свойств ядер производятся с помощью т. н. мик-роскопич. методов (Х а р т р и - Ф о к а м е т о д, метод случайной фазы, теория конечных ферми-систем и т. д.).
Лит.: Давыдов А. С., Теория атомного ядра, М., 1958; Му-хин К. Н., Экспериментальная ядерная физика, 5 изд., кн. 1-2, М., 1993; Мигдал А. Б., Теория конечных ферми-систем и свойства атомных ядер, 2 изд., М., 1983; Бор О., Моттельсон Б., Структура атомного ядра, пер. с англ., т. 1-2, М., 1971-77; Ситенко А. Г., Тартаковский В. К., Лекции по теории ядра, М., 1972; Широков Ю. М., Юдин Н. П., Ядерная физика, 2 изд., М., 1980; Айзенберг И., Грайнер В., Модели ядер, коллективные и одночастичные явления, пер. с англ., М., 1975; их же, Микроскопическая теория ядра, пер. с англ., М., 1976; Рейн-уотер Дж., Как возникла модель сфероидальных ядер, пер. с англ., "УФН", 1976, т. 120, в. 4, с. 529; Бор О., Вращательное движение в ядрах, пер. с англ., там же, с. 543; Моттельсон Б., Элементарные виды возбуждения в ядрах, пер. с англ., там же, с. 563; Соловьев В. Г., Теория атомного ядра. Ядерные модели, М., 1981; Михайлов В. М., Крафт О. Е., Ядерная физика, Л., 1988; Немец О. Ф. и др., Нуклонные ассоциации в атомных ядрах и ядерные реакции многонуклонных передач, К., 1988.
Ю. Ф. Смирнов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.