Akademik

SOLIDES (PHYSIQUE DES)

Ce qui différencie à première vue un solide des autres états de la matière (gaz, liquides, plasmas), c’est la résistance qu’il oppose à des forces mécaniques, sa tendance à garder un volume constant. De tout temps on s’est servi de cette propriété pour fabriquer des outils ou des armes. Les propriétés optiques des solides (couleur, transparence du verre, réflexion de la lumière par les métaux) sont également utilisées depuis très longtemps; mais ce n’est qu’assez récemment que les propriétés électriques, thermiques et magnétiques des solides ont pris un réel essor. Parmi les facteurs déterminants, il faut citer l’amélioration des techniques d’observation (diffraction des rayons X, microscopie électronique, technologie des basses températures, synthèse de cristaux), la mise au point de nombreuses applications industrielles et l’excellente compréhension théorique de l’état solide grâce au développement de la mécanique quantique. Celle-ci permet actuellement d’exprimer la plupart des propriétés des solides en fonction de quelques constantes universelles comme la charge électrique et la masse de l’électron et du proton, la constante de Planck 寮, etc. Les phénomènes thermodynamiques qui mettent en jeu la température ont été expliqués par les statistiques quantiques de Bose-Einstein et de Fermi-Dirac, qui s’appliquent respectivement à des particules à spin entier ou nul et à des particules à spin demi-entier.

L’observation des solides au moyen des rayons X permet de montrer qu’ils sont formés d’atomes de dimensions de l’ordre de l’angström (1 Å = 10^-8 cm). L’arrangement géométrique des atomes est dans beaucoup de cas la répétition triplement périodique d’un motif atomique ou moléculaire; il existe par suite trois vecteurs a¹, a², a³ tels qu’une translation T = n ¹a¹ + n ²a² + n ³a³, où n ¹, n ², n ³ sont des entiers, transforme le solide en lui-même; on dit qu’il existe dans ce cas un ordre cristallin à longue distance (cf. CRISTAUX - Cristallographie). D’autres solides (par exemple les verres), dits amorphes, ne présentent pas cet ordre. La plupart des solides s’obtiennent par refroidissement du liquide correspondant, et l’on peut évaluer le degré d’ordre introduit par la solidification en mesurant l’enthalpie H: le passage liquide-solide se produit en général à une température de fusion T^f bien définie, pour laquelle H(T) présente une discontinuité L (fig. 1) appelée chaleur de fusion; la quantité L/k T mesure le degré d’ordre (ou variation d’entropie) lors de la solidification, et l’on constate que, pour une catégorie de substances données, les métaux par exemple, celui-ci est constant; pour les verres, par contre, la transition liquide-solide est élargie, et le solide finalement constitué ressemble plus à un liquide figé désordonné qu’à un cristal.

L’ensemble des propriétés des solides est lié à la fois aux propriétés particulières des atomes, à l’arrangement géométrique de ceux-ci et à la mobilité des électrons dans le solide. Parmi celles qui dépendent plutôt de la nature des atomes et de leur arrangement géométrique, il faut citer les propriétés élastiques et plastiques, la propagation de vibrations sonores, la piézoélectricité, la ferroélectricité et la plupart des propriétés anisotropes des solides. Par contre, les propriétés électriques, thermiques et magnétiques dépendent surtout de la structure électronique du solide.

1. Cohésion des cristaux

Les effets des forces attractives interatomiques deviennent importants et conduisent à la formation de solides quand les atomes sont suffisamment proches et que la température est suffisamment basse. La forme générale du potentiel d’interaction V(r ) entre deux atomes est représentée sur la figure 2: le potentiel est attractif à grande distance, mais répulsif à courte distance. L’antagonisme de ces forces produit un minimum de V(r ), à une distance d’équilibre r ⁰ où les forces attractives et répulsives se compensent. Les forces qui déterminent la forme de V(r ) ont leur origine dans les interactions coulombiennes entre les charges positives des noyaux ou des ions et les charges négatives des électrons. L’apparente simplicité de cette formulation traduit mal la complexité du problème, qui fait intervenir des paramètres tels que la stabilité propre des atomes, les possibilités de transfert de charges entre atomes, la nature localisée ou délocalisée des électrons, l’anisotropie de la distribution des électrons autour des noyaux... Les principaux types de liaison ou de cristaux sont les tuivants.

Cristaux atomiques de Van der Waals

Les cristaux atomiques de Van der Waals sont formés à partir des atomes de gaz rares (hélium, argon) du tableau périodique des éléments. Ces atomes sont formés de couches électroniques très stables tournant autour du noyau. Chaque atome est donc équivalent à un dipôle tournant p (t ) qui est à la base de l’interaction dite de Van der Waals entre deux atomes. En effet, le champ électrique E(r ), d’ordre p (t )/r ³, produit par un premier atome, induit un dipôle 見E (cf. infra, Propriétés des solides ) dans un deuxième atome, ce qui produit une énergie d’interaction attractive:

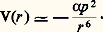
Aux courtes distances, quand les nuages électroniques commencent à se recouvrir, interviennent des forces répulsives qui s’expliquent par le principe de Pauli, selon lequel il est interdit à deux électrons de spin identique de se trouver dans le même état quantique. Les solides atomiques de Van der Waals cristallisent dans des structures cubiques; ce sont de bons isolants électriques, car les électrons sont fermement attachés aux atomes. La faible valeur de leur énergie de cohésion fait que ces substances peuvent être utilisées comme liquides réfrigérants. Indiquons également que la cohésion des cristaux moléculaires est assurée par des forces de Van der Waals.

Cristaux ioniques

Un atome de chlore Cl a une couche électronique externe où il ne manque qu’un électron pour en faire une couche complète. Un atome de sodium Na a, par contre, un seul électron sur sa couche externe. Dans le cristal ClNa, l’atome de sodium cède son électron exerne à l’atome de chlore pour donner deux ions Na⁺ et Cl^-. Ce transfert de charge, qui permet aux ions Na⁺ et Cl^- d’avoir des couches complètes, augmente l’énergie des deux atomes d’une quantité U = I 漣 A, où I est le potentiel d’ionisation de Na et A l’affinité de Cl; mais l’abaissement d’énergie résultant de l’interaction électrostatique attractive entre les deux ions l’emporte finalement. La cohésion des cristaux ioniques est supérieure à celle des cristaux de Van der Waals: ils cristallisent dans différentes structures cubiques dont le détail dépend surtout de la taille des ions positifs et négatifs. À part les sels du type ClNa, beaucoup d’oxydes, comme BeO, Al²³, sont des composés surtout ioniques et sont recherchés pour leur stabilité chimique. Certains composés ioniques sont solubles dans les solvants polaires tels que l’eau.

Cristaux covalents

La liaison covalente, d’origine quantique, est prépondérante dans les cristaux formés avec du carbone, du silicium et du germanium; elle explique également la stabilité de molécules telles que H², Cl² qui forment les cristaux moléculaires. Le cas le plus simple est celui de la molécule H²: chaque atome fournit un électron; et, dans la molécule, ces deux électrons se concentrent entre les deux protons pour profiter au maximum du potentiel attractif de ceux-ci. Le fort recouvrement des fonctions d’onde 祥(r) des deux électrons n’est possible que si les deux spins sont opposés; s’ils sont parallèles, le recouvrement est très faible et le potentiel V(r) ne présente pas de minimum (fig. 3). Cette liaison met une fois de plus en lumière l’importance du principe d’exclusion de Pauli. La contribution au potentiel d’interaction, dépendant de l’orientation des spins S¹ et S², peut s’écrire sous la forme:

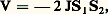
où J est appelée intégrale d’échange. Dans le cas d’atomes plus compliqués tels que ceux de carbone qui possèdent quatre électrons externes à une couche complète, on peut former quatre liaisons du type H² en composant les orbitales disponibles (c’est-à-dire 2s , 2p^x , 2p^y , 2p^z ) d’un atome donné avec des orbitales identiques d’atomes voisins. En effet, pour chaque atome C, quatre nouvelles orbitales dites hybrides du type 2s + 2p^x + 2p^y + 2p^z sont possibles, qui pointent dans les directions des sommets d’un tétraèdre et qui peuvent se recouvrir avec des orbitales d’atomes voisins situés dans ces directions. Ce procédé de recouvrement d’orbitales est répétable à l’infini pour constituer un cristal tridimensionnel, ayant la structure «cubique diamant» et où chaque atome a quatre voisins. C’est le cas du carbone sous la forme diamant, du germanium et du silicium. Une hybridation similaire permet de former le groupe |Si⁴|, responsable des propriétés physico-chimiques des silicates. Suivant le type d’hybridation, on a des cristaux où un atome donné a un seul voisin (par exemple la molécule H²), deux voisins (structures filamentaires de S, Se, Te), trois voisins (structures en couches du graphite et du phosphore).

Les caractéristiques essentielles des structures covalentes sont leur grande cohésion et la nature directionnelle des liaisons mises en jeu.

Liaison métallique

Dans les métaux et aux distances interatomiques concernées, le recouvrement des fonctions d’onde des électrons extérieurs est tellement fort qu’un électron donné n’appartient plus à un atome déterminé, mais est réparti dans tout le cristal. On dit qu’il est délocalisé; la théorie des bandes montre que cette délocalisation se traduit par une diminution de l’énergie cinétique du système qui est à la base de la stabilité des métaux. On peut se représenter un métal comme formé d’ions positifs fixes baignant dans un gaz d’électrons. Une telle liaison n’a pas de propriétés directionnelles bien nettes et elle dépend surtout de quantités globales, telles que les densités d’électrons et d’ions. Cela explique la facilité avec laquelle les métaux constituent les alliages. D’assez nombreux métaux cristallisent dans des structures cubiques compactes, chacun des atomes cherchant à s’entourer d’un nombre maximal de voisins.

Autres liaisons

D’autres types de liaisons existent, mais elles sont souvent des combinaisons des liaisons précédentes. Par exemple, la liaison hydrogène qui joue un grand rôle dans les substances organiques et biologiques est en grande partie ionique.

2. Structure électronique

Les électrons assurent non seulement la cohésion du cristal grâce à leur interaction avec les noyaux, mais ils interviennent de façon déterminante dans les propriétés de transport, les propriétés optiques, magnétiques... Il est donc important de bien connaître leur spectre d’énergie dans le cristal. C’est ce que se propose de faire la théorie des bandes, qui suit l’évolution des fonctions d’ondes électroniques quand on rapproche les atomes pour former le solide. Ces fonctions d’ondes, initialement localisées sur chaque atome, finissent par se recouvrir pour des distances suffisamment petites, ce qui permet aux électrons de sauter d’un atome à l’autre. Chaque électron se trouve ainsi délocalisé, et doit être décrit par une fonction d’onde 祥(r) s’étendant dans tout le volume du cristal. Une telle approximation s’applique bien en principe aux métaux et aux cristaux covalents, moins bien aux cristaux ioniques et de Van der Waals, mais elle fournit cependant un cadre général qui permet de comprendre l’ensemble des propriétés des solides. L’électron se déplace dans un potentiel V^c (r) qui a la symétrie du réseau cristallin et qui est dû à la fois aux ions fixés dans la structure cristalline et aux autres électrons. Le potentiel V^c (r) a alors la périodicité du réseau:

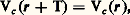
où:

Les niveaux d’énergie 﨎 que peut prendre l’électron sont solution de l’équation de Schrödinger:

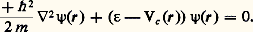
On remarque que, si 祥(r) est une solution du problème correspondant à une énergie 﨎, 祥(r + a) en est une aussi. En étendant ce raisonnement à un vecteur quelconque R du réseau, on montre que 祥(r) a nécessairement la forme:

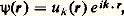
où:

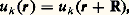
et:

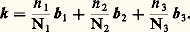
Les valeurs permises de k sont déterminées par la taille du solide: par exemple, L¹ = ¹a¹ est la longueur du cristal dans la direction a¹.

Les vecteurs bⁱ sont les vecteurs de base du réseau réciproque:

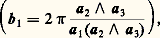
les nⁱ sont des nombres entiers ^{[cf. CRISTAUX]}.

De telles fonctions d’onde sont appelées fonctions de Bloch. On démontre de même que l’énergie 﨎 est une fonction périodique de k, c’est-à-dire:

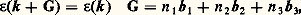
G étant un vecteur du réseau réciproque.

Approximation des liaisons fortes

Lorsque le recouvrement des fonctions d’ondes atomiques n’est pas trop fort, ce qui est le cas des couches 3d et 4d des éléments de transition (Fe, Pd), on peut prendre pour fonction d’onde 祥(r) une combinaison linéaire de fonctions d’ondes atomiques 祥ⁿ (r 漣 R^j ), solutions de l’équation de Schrödinger pour l’atome isolé:

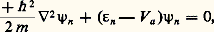
où V^a est le potentiel atomique et R^j représente la position des atomes. Si le recouvrement est suffisamment petit, on admet que 祥(r) est de la forme:

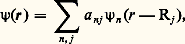
où il suffit de retenir, quand on étudie l’évolution d’un niveau atomique donné, 﨎¹ par exemple, les coefficients a^1j correspondants. Une telle fonction d’onde est une fonction de Bloch si les coefficients a^1j vérifient la relation a^1j = b ¹ exp (i k 練 R^j ).

L’énergie correspondante se met sous la forme (pour les cristaux cubiques):

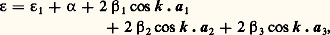
avec:

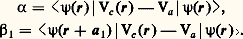
Les grandeurs 見 et 廓 sont des éléments de matrice faisant intervenir la différence entre le potentiel périodique V(r) et le potentiel atomique V^a . On voit donc que le niveau atomique 﨎¹ est élargi en une bande de largeur 2( 廓¹ + 廓² + 廓³).

Si l’on a plusieurs niveaux atomiques au départ, on obtient un ensemble de bandes d’énergies permises séparées par des bandes d’énergies interdites (fig. 4). On montre que si on a un solide formé de N atomes, chaque bande peut contenir (2 l + 1)N niveaux, donc 2 (2 l + 1)N électrons (2 l + 1 est la dégénérescence orbitale du niveau atomique, alors que le facteur 2 provient de la statistique de Fermi-Dirac qui autorise au maximum deux électrons de spin opposé par niveau). La figure 5 montre que l’énergie de cohésion des métaux de transition 5 d passe par un maximum quand on remplit progressivement cette bande: cela est en accord avec l’énergie d’ordre 廓 gagnée en délocalisant les électrons.

Approximation des électrons libres et presque libres

Pour les électrons provenant d’états atomiques excités, 4s par exemple, le recouvrement des fonctions d’onde est tellement important qu’il vaut mieux décrire les électrons à l’aide d’ondes planes 祥(r) = e ^{i k.r} et négliger le potentiel périodique V(r). Cette hypothèse est partiellement justifiée par le fait que l’énergie cinétique de ces électrons est tellement grande qu’ils ne sont pratiquement plus sensibles au potentiel V(r). Les énergies des électrons sont alors de la forme: 﨎 = (face=F0019 寮²/2m )k ².

On obtient ainsi une bande d’énergie, de largeur infinie, avec des états occupés de k = 0 jusqu’à une valeur maximale k = k^F qui dépend du nombre d’électrons présents; la grandeur k^F est appelée le vecteur d’onde de Fermi, l’énergie correspondante est l’énergie de Fermi. Beaucoup de métaux simples (Na, Pb...) obéissent bien au modèle des électrons libres, et 﨎^F est de l’ordre de 5 à 10 eV. Quand on introduit le potentiel périodique V(r), comme une perturbation, celui-ci est particulièrement actif quand le vecteur k est dans une région où la condition de réflexion de Bragg est réalisée, c’est-à-dire lorsqu’on a:

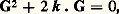
où G est le vecteur du réseau réciproque.

L’allure des solutions 﨎(k ) est représentée sur la figure 6; on notera à nouveau la présence de bandes d’énergie interdites quand la condition de Bragg est réalisée.

Métaux, isolants et semiconducteurs

Prenons le cas d’une bande formée dans un cristal de N atomes et pouvant contenir 2 N électrons: si le nombre d’électrons est juste égal à 2 N, on dit que la bande est pleine. Comme celle-ci est séparée de la bande suivante, vide, par une bande interdite, un faible champ électrique E n’est pas capable d’accélérer de tels électrons, car ils ne peuvent pas changer leur énergie. On dit qu’on a un isolant électrique. Si, par contre, le nombre d’électrons est inférieur à 2 N, on a un métal, car l’intervalle 﨎 entre deux niveaux successifs est infiniment petit. Si la bande interdite entre la dernière bande pleine, dite bande de valence, et la bande suivante vide est petite devant l’énergie thermique k T, des électrons peuvent être excités thermiquement dans cette bande, appelée bande de conduction, où ils pourront être accélérés par un champ électrique: on dit alors qu’on a un semi-conducteur intrinsèque (ex. Ge, Si). Ce schéma introduit la notion importante de trou dans une bande de valence incomplètement remplie: on montre que de tels trous se comportent au point de vue électrique comme des particules de masse et de charge positives.

Surface de Fermi et zones de Brillouin

Pour des électrons libres, les surfaces d’énergie 﨎 = constante dans l’espace des k sont des sphères. Au zéro absolu, tous les états occupés sont à l’intérieur de la sphère de Fermi. Pour des électrons non libres, on peut aussi définir une surface de Fermi contenant tous les états occupés. Celle du cuivre est représentée sur la figure 7. Seuls les électrons au voisinage de cette surface sont capables de réagir à des forces extérieures (les électrons internes ne pouvant pas changer facilement d’énergie), d’où l’importance de cette surface. On sait par ailleurs que 﨎(k ) présente des discontinuités chaque fois que k satisfait à la condition de Bragg: les vecteurs k correspondants sont ceux dont l’extrémité se termine sur un plan bissecteur de G. La figure 8 montre ces plans pour un réseau à deux dimensions. On définit alors ce qu’on appelle des zones de Brillouin: la première zone s’obtient en considérant les vecteurs G équivalents les plus courts; dans l’espace à trois dimensions, les zones de Brillouin sont des polyèdres (fig. 7). À l’intérieur de chaque zone, 﨎(k ) est une fonction continue de k . Suivant le nombre d’électrons présents, la surface de Fermi est contenue dans la première zone ou empiète sur les zones suivantes. Il est possible, dans les métaux purs, de déterminer la forme de la surface de Fermi par des techniques expérimentales (telles que la mesure de la magnétorésistance, du diamagnétisme, de la résonance cyclotron) qui sont sensibles au mouvement des électrons dans un champ magnétique H: le vecteur k évolue suivant l’équation:

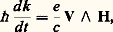
qui montre que l’extrémité de k se déplace sur une surface d’énergie constante et dans un plan perpendiculaire à H. Différents types d’orbites peuvent être observés si on se rappelle que 﨎(k + G) = 﨎(k ) (fig. 6 et 7): elles sont soit fermées, soit ouvertes si les courbes 﨎(k ) rencontrent les zones de Brillouin. Les techniques énoncées ci-dessus sont surtout sensibles aux orbites fermées extrémales et aux orbites ouvertes.

Limites de l’approximation des électrons indépendants

On néglige, dans la théorie des bandes ainsi exposée, l’effet des interactions entre électrons, c’est-à-dire que chaque électron se déplace indépendamment des autres. Cette approximation est à peu près justifiée dans les métaux simples, où l’interaction entre deux électrons est fortement écrantée par la présence des autres. Dans les métaux de transition, par contre, on observe du magnétisme spontané qui ne s’explique qu’à partir de ces interactions. On montre qu’on minimise, du point de vue de l’énergie, l’effet de ces interactions répulsives en localisant les électrons sur les atomes, ce qui veut dire que l’état métallique n’est vraiment possible que si ces interactions ne sont pas trop fortes par rapport à la largeur de bande 廓. On peut expliquer de cette façon le caractère isolant électrique de nombreux oxydes de transition (par exemple NiO) qui ont pourtant des couches atomiques incomplètes. Les transitions isolant-métal (ou transitions de Mott) observées dans certains cas doivent être attribuées à la compétition entre états délocalisés et états localisés.

3. Élasticité et phonons

Élasticité, critère de rupture

Chaque atome se trouve au fond de son puits de potentiel (fig. 2) dans le cristal au repos. L’application de contraintes 靖 provoque des déformations proportionnelles à la contrainte tant que les déplacements atomiques u restent petits. On a alors un comportement élastique, car tous les atomes reviennent à leur position d’équilibre si on supprime 靖. On obtient ainsi une déformation:

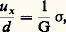
dans le cas d’un cisaillement suivant l’axe x (fig. 9). G est appelé module de rigidité. On peut également estimer la contrainte critique nécessaire pour faire glisser un plan atomique sur un autre, c’est-à-dire pour obtenir la rupture du cristal (déformation non élastique). On trouve une valeur d’ordre Ga /2 神d , d’autant plus faible que les plans sont plus compacts: de tels ordres de grandeur sont effectivement observés dans des cristaux absolument parfaits mais, dans la plupart des cas, on obtient des valeurs beaucoup plus faibles liées à la présence de dislocations.

Vibrations atomiques ou phonons

Le potentiel d’interaction V(r) est également responsable de l’existence de modes de vibrations collectifs, ou phonons, susceptibles de se propager à travers tout le solide. Les déplacements atomiques sont de la forme:

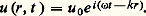
Ce sont donc des ondes progressives caractérisées par une courbe de dispersion 諸 = 諸(k ) qui définit les fréquences de vibrations permises en fonction de la longueur d’onde = 2 神/k . Il est important de remarquer que les fréquences sont bornées supérieurement, c’est-à-dire 諸 諒 諸^D, où 諸^D est ce que l’on appelle la fréquence de Debye. L’énergie et la quantité de mouvement d’un phonon à la fréquence 諸 sont quantifiées en unités de 寮 諸 et 寮k , respectivement ^{[cf. PHONON]}.

4. Thermodynamique et chaleur spécifique des solides

L’énergie totale d’un cristal au repos est égale à U⁰ = N V⁰ (fig. 2). Cela n’est vrai qu’au zéro absolu. À température finie, il nous faut tenir compte de l’excitation thermique des électrons et des phonons qui apportent une contribution positive à l’énergie totale:

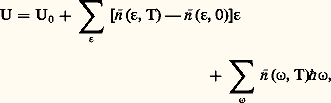
讀 ( 﨎, T) et 讀 ( 諸, T) étant respectivement les populations thermiques des niveaux électroniques d’énergie 﨎 et des niveaux de vibration d’énergie 寮 諸: elles sont données respectivement par la statistique de Fermi-Dirac et celle de Bose-Einstein. À partir de là, on peut définir une chaleur spécifique C^v = d U/d T. On trouve ainsi :

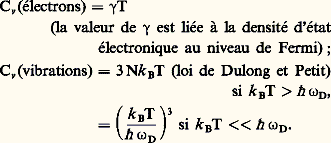
Ondes de densité

Dans un certain nombre d’isolants et de métaux, on observe que la fréquence de vibration de certains modes dépend fortement de la température et s’annule en dessous d’une certaine température T^c (cf. PHONON - Instabilités structurales). Ces modes, dits mous, se figent en dessous de T^c en une onde de densité statique u 黎 u ⁰ e ^{i (k 0r +} size=1^淋). Particulièrement intéressants sont les cas où la périodicité de cette onde est incommensurable avec celle du réseau cristallin: on peut montrer qu’il existe alors, en dessous de T^c , deux nouvelles classes d’excitations 諸(k ⁰ 梁 q ) qui correspondent à des fluctuations temporelles de la phase 淋 – on parle alors de phasons – ou de l’amplitude – les amplitudons (fig. 10). De telles excitations ont été clairement mises en évidence dans le composé ThBr⁴. L’onde de densité est accompagnée dans les métaux d’une modulation similaire de la densité de charge électronique: le phason, dans la limite q0, correspond alors à un glissement de la densité de charge qui ne s’accompagne pas forcément d’effets dissipatifs (supraconductivité de Fröhlich). Les prémices de ce type de conductivité ont été observés dans le métal organique TTF-TCNQ.

5. Propriétés des solides

On vient de voir quels étaient les niveaux d’énergie possible du système ions + électrons et comment ces niveaux sont occupés en fonction de la température. On va maintenant envisager comment le solide répond à des perturbations telles que gradient de température, champ électrique et champ magnétique.

Conductibilité thermique des solides

Si l’on établit un gradient de température d T/d X le long d’un solide de 1 centimètre de long et 1 centimètre carré de section, on peut observer un écoulement de chaleur d Q/dt = K(d T/d X), où K est par définition la conductibilité thermique. Un modèle simple montre que K = 1/3(CVl ), où C est la chaleur spécifique, V la vitesse des particules transportant la chaleur et l leur libre parcours moyen, c’est-à-dire la distance moyenne que parcourt une particule avant de subir un choc. À température ambiante, on constate que les métaux conduisent mieux la chaleur que les isolants électriques: cela tient au fait que, dans les premiers, la chaleur est transportée à la fois par les électrons et les phonons, alors que ces derniers seuls sont efficaces dans les isolants. La figure 11 indique l’allure générale des courbes K(T) déterminées par les variations thermiques de C(T) et l (T). Le libre parcours moyen, aussi bien des électrons que des phonons, est surtout limité par les chocs qu’ils subissent avec d’autres phonons. Aux hautes températures (T 礪 ^D), le nombre de phonons f ( 﨎) qui ont une énergie 﨎 = 寮 諸 est égal à k T/ 寮 諸, d’où un libre parcours moyen l (T) 力 1/T. l (T) tend en général vers une constante à basse température au lieu d’aller vers l’infini, en raison de la présence d’impuretés. Les variations opposées de l (T) et de C(T) expliquent l’allure de la variation de K(T).

Conductibilité électrique des métaux

La vitesse V d’un électron de conduction, sous l’action d’un champ électrique E, évolue suivant l’équation:

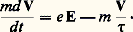
Le deuxième terme du second membre décrit les chocs que subit un électron, par l’intermédiaire d’un temps de relaxation 精 lié au libre parcours moyen l par 精 = l /V^F. Le fait que ce soit la vitesse de Fermi qui intervienne indique que seuls les électrons à la surface de Fermi peuvent participer à des collisions (fig. 12); sous l’action de E, la sphère de Fermi se déplace avec une vitesse 寮(d k/dt ) = e E, et ce déplacement est contrecarré par le transfert d’électrons de A en B, à la suite des collisions qu’ils subissent. Il s’établit finalement une distribution d’équilibre telle que d k/dt = 0. La vitesse des électrons tend alors vers une constante:

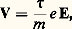
d’où une densité de courant j = 靖E (loi d’Ohm). La conductivité 靖 est égale à ne ² 精/m , où n est le nombre d’électrons par centimètre cube.

A priori, on aurait pu penser que les électrons subissent des collisions sur les atomes, ce qui donnerait un libre parcours de l’ordre d’une distance interatomique. En fait, il n’en est rien, car, pour un cristal parfait, les électrons sont décrits par des ondes de Bloch qui peuvent traverser le réseau sans être diffusées (conductivité parfaite). Mais la périodicité parfaite du réseau est rompue par la présence des phonons produisant un libre parcours moyen inversement proportionnel au nombre de phonons: aux hautes températures, l (T) varie donc comme 1/T. À basse température, l (T) tend à nouveau vers une constante, en raison de la présence d’impuretés (fig. 13).

Pour les semiconducteurs intrinsèques, 靖 est nul à T = 0, mais, dès que T 0, des électrons sont excités dans la bande de conduction pour donner une conductivité finie qui augmente avec T (fig. 14).

Propriétés optiques. Constante diélectrique

Un champ électrique alternatif E( 諸) agit avant tout sur les électrons et crée une polarisation électrique P = np = n 見E, où n est le nombre d’atomes par unité de volume, p le nombre dipolaire par atome et 見 la polarisabilité. 見 est d’autant plus grande que l’électron est moins lié à l’atome; elle dépend donc de la facilité avec laquelle cet électron peut changer d’énergie. Si E( 諸) est un champ électrique à la fréquence 諸/2 神, on montre que:

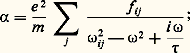
戀

寮 諸^ij est la différence d’énergie entre les états excités j et l’état fondamental i de l’électron considéré, f^ij est la force d’oscillateur de la transition dipolaire électrique correspondante, 精 est un temps de relaxation décrivant les effets dissipatifs auxquels est soumis l’électron.

La constante diélectrique 﨎( 諸) est liée à 見 par la relation de Clausius-Mossoti:

l’indice de réfraction n ( 諸) est à son tour relié à 﨎( 諸) par n ²( 諸) = 﨎( 諸).

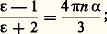
La présence d’effets dissipatifs fait que 﨎( 諸) présente une partie réelle et une partie imaginaire. La partie réelle de n ( 諸) décrit la vitesse de propagation de la lumière V = c /n ( 諸) dans le solide et, si n ( 諸) est anisotrope (par suite d’une anisotropie du réseau cristallin par exemple), elle intervient dans des phénomènes comme la biréfringence et l’activité optique. Au voisinage de 諸 = 諸^ij , les effets dissipatifs deviennent importants, on dit qu’il y a absorption de la lumière: les photons d’énergie 寮 諸^ij transmettent leur énergie à l’électron, qui effectue une transition de l’état i vers l’état j (fig. 14 a). Cette absorption est à l’origine de la couleur des cristaux.

Le comportement diélectrique des métaux et des cristaux ioniques mérite une mention particulière:

– Pour les métaux, on peut prendre 諸^ij 力 0 et distinguer les deux domaines de fréquence 諸 廉 1/ 精 et 諸 拾 1/ 精. Dans le premier cas, 見 est imaginaire, et l’on explique de la sorte des phénomènes tels que l’effet de peau, la réflexion de la lumière par les métaux; dans le second cas, 見 est réel, et l’on explique ainsi la transparence des métaux aux rayons X.

– Les cristaux ioniques, en plus de la polarisabilité électronique 見, présentent une polarisabilité ionique 廓 due au déplacement relatif des ions positifs par rapport aux ions négatifs. Par suite de la différence de masse importante entre les ions et les électrons, les deux types de polarisation ont des comportements différents en fonction de 諸, et l’on démontre la relation de Lyddane-Sachs-Teller:

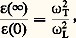
où 﨎(face=F0019 秊) est la constante diélectrique aux hautes fréquences, et où 諸^T et 諸^L sont les fréquences de vibrations optiques transverses et longitudinales dans la limite k = 0. Dans certains cristaux ioniques, 諸^T tend vers 0 en fonction de la température et, dans ce cas, 﨎(0) peut tendre vers l’infini: le cristal devient alors ferroélectrique.

Mentionnons également le fait qu’un isolant peut devenir conducteur de l’électricité quand on l’irradie avec une lumière qui induit des transitions bande à bande (fig. 14 a). Ce phénomène, appelé photoconductivité, est largement utilisé dans les batteries solaires.

Effets d’un champ magnétique. Paramagnétisme

Les électrons ont, associé à leur moment cinétique de spin, un moment magnétique 猪 = g S 猪^B (g = 2, 猪^B = magnéton de Bohr).

Lorsque plusieurs électrons sont localisés sur un atome, il faut ajouter les moments magnétiques de spin et les moments magnétiques orbitaux suivant les règles de Hund pour obtenir un moment résultant 猪. Quand ce moment est placé dans un champ magnétique H, il prend une énergie 漣 猪H qui tend à l’orienter dans la direction de H. Cette orientation est combattue par la température, et l’aimantation totale:

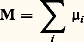
est de la forme M = 﨑H, où 﨑 est la susceptibilité paramagnétique. Pour des moments localisés sur des atomes, on trouve 﨑 = n 猪²/3k T, alors que, pour des électrons libres, seule une fraction ^F (où k ^F = 﨎^F) des électrons à la surface de Fermi peuvent être orientés dans H, d’où une susceptibilité indépendante de T. Les deux types de comportement sont observés respectivement dans les sels magnétiques et les métaux.

Magnétisme spontané et supraconductivité

Parmi les propriétés qui ne peuvent pas être décrites par le seul modèle des bandes, mais pour lesquelles il faut tenir compte de manière précise des interactions entre électrons, on citera plus spécialement les phénomènes magnétiques spontanés et la supraconductivité.

Magnétisme spontané

On a déjà vu (fig. 3) que les interactions entre deux atomes pouvaient dépendre de l’orientation des spins des électrons: si cette interaction est grande devant l’énergie thermique, l’ensemble des moments magnétiques 猪 est susceptible de prendre des configurations simples. Si tous les moments magnétiques s’orientent parallèlement, on dit que le solide est ferromagnétique: dans ce cas, M est différent de 0, même si l’on a H = 0; si les moments pointent alternativement dans un sens et dans l’autre, on a une substance antiferromagnétique. Des structures magnétiques plus compliquées, par exemple hélicoïdales, sont également observées. Dans tous les cas, les phénomènes magnétiques spontanés disparaissent au-dessus d’une température critique T^c quand le désordre thermique l’emporte sur les interactions. On a vu que, pour l’hydrogène, l’intégrale d’échange J était négative, favorisant ainsi l’antiferromagnétisme: on observe, en fait, que la plupart des sels et des oxydes isolants contenant des ions magnétiques sont antiferromagnétiques. L’origine des interactions est cependant plus compliquée que dans le cas de H² et fait intervenir des transferts d’électrons via des atomes intermédiaires non magnétiques. Beaucoup de métaux (Fe, Co, Ni), par contre, sont ferromagnétiques: les électrons responsables sont ceux des bandes 3d . Si deux électrons de cette bande se trouvent sur un même atome, ils n’ont pas la même énergie quand leurs spins sont antiparallèles ou parallèles; dans le premier cas, les deux électrons peuvent entrer dans une même orbitale quantique, alors qu’ils ne le peuvent pas dans le second: l’interaction coulombienne favorise, dans ce cas, un arrangement ferromagnétique. La condition d’apparition du magnétisme spontané s’écrit:

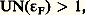
où N( 﨎^F) est la densité d’états au niveau de Fermi. Cette condition exprime que le gain d’énergie U quand on retourne un spin compense l’augmentation d’énergie cinétique qui en résulte. D’autres types d’interactions sont possibles dans les métaux de terres rares, où les ions magnétiques 4f sont trop éloignés les uns des autres pour que leurs fonctions d’onde se recouvrent: l’interaction entre les ions magnétiques se fait alors via les électrons de conduction.

Il y a dans les ferromagnétiques, en plus de l’énergie d’échange responsable du parallélisme des moments, d’autres termes d’énergie tels que l’énergie d’anisotropie et l’énergie magnétostatique qui fixent l’orientation de M par rapport aux axes du cristal; on dit qu’il y a des directions de facile et difficile aimantation: il faut appliquer un couple magnétique minimal pour sortir l’aimantation d’une direction de facile aimantation. Ces mêmes énergies permettent de comprendre pourquoi un composé ferromagnétique préfère se diviser en domaines d’aimantations opposées.

Supraconductivité

Une autre transition de phase est observée à basse température (T 麗 20 K) dans de nombreux métaux ou alliages tels que Pb, Sn, Nb, Nb³Sn...: en dessous d’une température critique T^c , la résistivité électrique 福 s’annule. D’autres phénomènes se produisent en même temps: exclusion de champ magnétique (effet Meissner), apparition d’une bande d’énergie interdite. L’origine de cette transition réside dans des interactions électron-électron via les phonons: un électron se déplaçant dans un cristal attire pour un moment les ions vers des positions déplacées; dans cette région règne momentanément une densité de charge positive capable d’attirer un deuxième électron qui se trouve ainsi indirectement attiré vers le premier. Sous l’action de cette force attractive, les électrons se groupent par paires, de moment cinétique et magnétique nul. Quand on envoie un courant dans un supraconducteur, toutes les paires prennent une même quantité de mouvement et il devient très difficile d’arrêter un tel courant, car il faut soit briser des paires, soit freiner en même temps et de la même manière toutes les paires. On dit que le métal est supraconducteur, il ne présente plus de résistivité électrique. L’application de densités de courant ou de champs magnétiques trop forts détruit l’état supraconducteur et rétablit l’état métallique normal.

Métaux organiques

Des propriétés métalliques ainsi que des transitions métal-isolant et métal-supraconducteur ont été observées (fig. 15) dans des matériaux organiques ne contenant aucun atome ou ion traditionnellement associé à cet état. Ce sont des composés formés de chaînes linéaires légèrement couplées entre elles où la conductivité se fait principalement le long de ces chaînes.

Il est permis de penser que ces matériaux connaîtront un essor un peu analogue à celui des alliages, compte tenu des nombreuses possibilités offertes par la chimie organique de modifier progressivement leurs propriétés en remplaçant, par exemple, certains groupements moléculaires par d’autres. Mentionnons également que des dopages de type n ou p sont capables de produire une conduction métallique dans des semiconducteurs en chaîne du type (CH)^x .

6. Défauts dans les solides

Les propriétés du solide parfait peuvent être fortement altérées par la présence de défauts, et, parfois, des propriétés entièrement nouvelles apparaissent. Il est en réalité très difficile d’en faire une étude complète; on mentionnera simplement les défauts les plus importants. On peut distinguer a priori deux sortes de défauts: les défauts de structure du réseau cristallin et les impuretés (atomes de nature différente; cf. CRISTAUX – Défauts dans les cristaux).

Dislocations

L’expérience montre que les métaux supportent des déformations permanentes sans casser, contrairement aux cristaux ioniques et covalents, qui sont dit fragiles. Les contraintes nécessaires pour produire les déformations sont par ailleurs très inférieures à celles qu’on a estimées au chapitre 3. L’origine de ces comportements est liée à la présence d’un type de défaut particulier, les dislocations. C’est un défaut étendu linéaire qui correspond, dans le cas d’une dislocation coin, à l’introduction d’un plan supplémentaire dans une partie du cristal (fig. 16). Le mouvement de ces dislocations sous l’action de contraintes permet d’obtenir des déformations permanentes sans qu’il soit nécessaire de faire glisser rigidement des plans atomiques les uns sur les autres. La résistance au mouvement des dislocations est faible pour les métaux, mais forte pour les cristaux ioniques et covalents, un fait directement relié au type de liaison.

Lacunes et interstitiels

Lorsqu’on approche du point de fusion d’un solide, plusieurs types de défauts ponctuels se forment, les plus courants étant les lacunes, quand un atome manque à un nœud du réseau (défaut de Schottky), ou des interstitiels, quand un atome occupe une position différente d’un nœud du réseau (défaut de Frenkel). À chaque température T il existe une concentration d’équilibre de tels défauts. Ils jouent un rôle essentiel dans la conductivité électrique des cristaux ioniques et dans tous les phénomènes de diffusion atomique.

Solides amorphes et très désordonnés

Les solides amorphes sont des solides qui ne présentent pas l’arrangement périodique des atomes observés dans des cristaux. Citons les verres, où aucun arrangement périodique ne se forme à cause de la grande viscosité du liquide, et les solides condensés sur des supports froids. Dans les solides amorphes, le libre parcours moyen des électrons et des phonons est très court, de l’ordre de la distance interatomique; ce sont donc en général de mauvais conducteurs de l’électricité et de la chaleur. Plus précisément, on peut montrer que le désordre atomique tend à localiser les fonctions d’ondes électroniques dans les métaux, un effet particulièrement prononcé dans des structures bi- ou unidimensionnelles. Les faibles libres parcours moyens électroniques amplifient également l’importance des interactions électron-électron, ce qui accentue à son tour la tendance à la localisation. Parmi les autres comportements spécifiques de l’état désordonné, signalons l’absence de dislocations, un défaut du cristal, et l’apparition systématique d’une nouvelle classe d’excitations, appelée défauts tunnels, dont l’origine n’était pas encore bien élucidée au début des années 80.

Impuretés dans les métaux

Suivant la concentration d’impuretés C, on parle d’alliages dilués (C 麗 1 p. 100) ou concentrés. La liaison métallique est très favorable à la formation de tels alliages, et le fait que le paramètre essentiel dans les alliages concentrés soit la densité électronique plutôt que l’entourage particulier des atomes a permis de comprendre les changements de phase cristalline qui se produisent dans des alliages tels que Cu-Zn: l’adjonction de Zn augmente le nombre d’électrons et change donc la position relative de la surface de Fermi et de la première zone de Brillouin; les changements de phase se produisent en fait quand la surface de Fermi touche la zone de Brillouin. Dans les alliages dilués, l’impureté isolée diffuse des électrons de conduction et elle est responsable de la résistivité électrique résiduelle (à T = 0) proportionnelle à C, observée dans les alliages. La longue portée des interactions entre impuretés, qui se fait via les électrons de conduction, est un autre caractère de l’état métallique et conduit à des effets intéressants si les impuretés sont magnétiques (magnétisme de verre de spins).

Impuretés dans les semiconducteurs

On peut augmenter la conductivité électrique des semiconducteurs, tels que le silicium et le germanium intrinsèques, de plusieurs ordres de grandeur (fig. 14), par l’addition de faibles quantités d’impuretés; celles-ci peuvent être divisées en deux catégories, les atomes donneurs et les atomes accepteurs d’électrons. Dans la première catégorie, il faut placer les impuretés pentavalentes (As, Sb). Si un atome d’arsenic par exemple occupe un point du réseau, seuls quatre électrons forment des liaisons avec les voisins et le cinquième électron se déplace dans le potentiel coulombien de l’impureté: l’énergie de liaison correspondante est très faible, car elle est réduite d’un facteur 﨎² 黎 100 ( 﨎 = constante diélectrique) par rapport à ce qu’elle serait dans un atome isolé. Cela revient à dire que cet électron se trouve dans un niveau d’énergie situé sous la bande de conduction, à environ 10^-2 eV de celle-ci: un tel électron est excité thermiquement dans la bande de conduction aux températures usuelles; on a alors un semiconducteur n . Les impuretés trivalentes (Al, Ga) forment de même des niveaux accepteurs d’électrons au voisinage de la bande de valence avec formation de trous dans celle-ci. On dit qu’on a un semiconducteur p (fig. 14b). Les semiconducteurs n et p ont été le point de départ de nombreuses applications qui ont révolutionné l’électronique.

Impuretés dans les isolants

Les impuretés dans les isolants affectent en particulier leurs propriétés optiques. La couleur de substances, telles que le diamant, ou d’oxydes, tels que Al²³, est due à de très faibles quantités d’atomes étrangers. La couleur rouge du rubis (Al²³) provient des impuretés de chrome absorbant dans le bleu; un autre centre coloré bien connu est le centre F des cristaux ioniques, qui est constitué par un électron piégé dans une lacune négative. Les rubis sont également utilisés dans les lasers. Quand on irradie un rubis avec de la lumière bleue, des électrons sont excités vers un niveau supérieur d’où ils retombent d’abord dans un niveau intermédiaire, ensuite dans le niveau fondamental. Cette dernière émission, qui se fait dans le rouge, est stimulée par la présence de lumière ayant la fréquence correspondant à cette transition.

Les isolants dopés par des impuretés possèdent une autre propriété importante: ils peuvent être luminescents; irradiés avec une lumière de fréquence 益¹, ils émettent de la lumière à une fréquence 益² 麗 益¹ (l’irradiation lumineuse est remplaçable d’ailleurs par d’autres types d’excitation). Si la réémission à la fréquence 益² suit immédiatement l’excitation, on parle de fluorescence, et, si elle se produit avec un retard pouvant atteindre plusieurs heures, il s’agit de phosphorescence. La figure 14 c indique un mécanisme possible pour ce retard, qui met en jeu la migration de la lacune produite par l’irradiation initiale vers un niveau de défaut.