Akademik

STABILITÉ

Pour un ensemble mécanique (D), dont la situation par rapport à un repère galiléen (g ) est caractérisée par la donnée de n paramètres géométriques indépendants (q ¹, ..., qⁱ , ..., qⁿ ), la connaissance des conditions initiales et des champs de forces à distance ainsi que l’intervention d’hypothèses sur les efforts de liaison (lorsque de tels efforts se manifestent) permettent d’établir des prévisions qⁱ = fⁱ (t ) par intégration des équations régissant les mouvements possibles de (D).

Si l’on modifie un peu les conditions intiales, c’est-à-dire les valeurs: qⁱ (0) et dqⁱdt (0) = q ⁱ (0), ou si l’on modifie les champs de forces à distance, tout en conservant les mêmes hypothèses sur les efforts de liaison, on établit des prévisions:

La question est de savoir si tous les 﨎ⁱ (t ) restent petits dans le déroulement évolutif des phénomènes. S’il en est ainsi, on dira que le mouvement de (D), prévu et caractérisé par qⁱ = fⁱ (t ), avec i = 1, ..., n , est stable . Il y a lieu de préciser les locutions: «modifier un peu» et «rester petit» qui ont une signification intuitive, ce qui ne saurait suffire à élaborer une théorie valable.

Le problème présente de l’intérêt, car les conditions initiales et les champs à distance sont connus et fournis à partir de mesures expérimentales, et une prédiction analytique stricte est donc impossible (en particulier, il y a lieu de distinguer entre les conditions initiales voulues et celles qui sont effectivement réalisées).

Souvent, les mouvements sont simples ou bien les variables choisies pour les décrire s’expriment simplement en fonction du temps. Les deux cas les plus fréquents sont les suivants:

– tous les qⁱ sont prévus comme devant rester constants, c’est-à-dire indépendants du temps:

on dit alors que l’on prévoit un équilibre de (D) dans le repère (g ), la question qui se pose étant celle de la stabilité de cet équilibre ;

– parmi les qⁱ de l’ensemble configuratif (q ), certains sont prévus comme devant rester constants (par exemple les p premiers pour fixer les idées), les autres le sont comme devant être des fonctions du premier degré par rapport au temps:

on dit alors que l’étude concernant (D) conduit à la prévision d’un état stationnaire de (D) dans le repère (g ), et la question qui se pose est liée à la stabilité de cet état stationnaire .

Les définitions des termes doivent être précisées; quelques exemples particuliers doivent être explicités a priori, et quelques théorèmes généraux énoncés et appliqués; mais la question générale reste complexe: elle est la préoccupation d’un grand nombre de chercheurs mathématiciens, physiciens et techniciens. Son domaine d’applications est vaste et comprend, entre autres, l’astronomie classique, la balistique classique et récente, notamment les engins spéciaux, les lanceurs et les satellites (cf. ASTRODYNAMIQUE, MISSILES).

On peut toujours poser:

ou:

ces deux cas étant usuels dans le fonctionnement des appareillages industriels.

Dans des exemples plus difficiles, ce sont des fonctions assez compliquées des qⁱ et des q ⁱ , à savoir:

qui vont garder, dans la prévision, des grandeurs constantes 諸^j (0). Ainsi en sera-t-il de certaines des composantes P, Q et R du taux de rotation galiléen d’un solide. Le problème est donc généralement très complexe et l’exposé suivant ne prétend qu’à une information initiatrice.

1. Exemple issu de la dynamique du solide

Un solide (S) est dit animé d’un mouvement à la Poinsot si l’un de ses points ^S reste immobile dans un repère galiléen et si le moment en ^s du torseur des efforts extérieurs agissant sur (S) est nul.

Lorsque le mouvement à la Poinsot d’un solide (S) se fait spontanément autour d’un axe immobile dans un repère galiléen, cet axe doit être un axe principal d’inertie de (S) au point fixé O = ^s = O^g , et il en résulte que le taux de rotation ^sg est constant dans (S) et dans (g ). Inversement, une rotation est un mouvement à la Poinsot si et seulement si c’est une rotation uniforme autour d’un axe principal d’inertie en O. Ainsi:

– dans le cas où A, B, C (moments d’inertie par rapport aux trois axes principaux en O; cf. CINÉTIQUE) sont tous différents, on trouve les rotations uniformes autour de l’un des trois axes principaux Ox 轢^s, Oy 轢^s, Oz 轢^s;

– dans le cas où A = B C, on trouve les rotations uniformes autour de Oz 轢^s et les rotations uniformes autour d’un axe quelconque perpendiculaire en O à Oz 轢^s;

– dans le cas où A = B = C, on trouve les rotations uniformes autour de n’importe quel axe passant par O.

Supposons donc que (S) soit animé d’une rotation uniforme de vitesse angulaire ゚ autour d’un de ses axes principaux. Désignons cet axe par Ou 轢^s, lié à (S), et soit ゎ^g la position qu’il conserve dans le galiléen au cours de la rotation considérée. On fait l’hypothèse qu’entre deux dates t ⁰ et t ¹ une perturbation (percussion, par exemple) intervient à l’issue de laquelle (S) est de nouveau animé d’un mouvement à la Poinsot. Si la perturbation est assez faible pour qu’à la date t ¹ l’axe Ou 轢^s soit encore voisin de Ou 轢^g et ^sg voisin de 諸 ゎ^s, on doit se demander si le mouvement ultérieur laissera Ou 轢^s voisin de Ou 轢^g et ^sg voisin de 諸 ゎ^s.

Dans le cas où A 礪 B 礪 C, la réponse est affirmative si Ou 轢^s est soit Ox 轢^s, soit Oz 轢^s (c’est-à-dire l’axe principal de plus grand ou de plus petit moment d’inertie); la réponse est négative si Ou 轢^s est Oy 轢^s (c’est-à-dire l’axe principal de moment d’inertie intermédiaire). Ces résultats proviennent de la représentation de Poinsot: si la perturbation s’exerce sur une rotation autour de Ox 轢^s (ou Oz 轢^s), l’axoïde lié au solide (S) est un cône de sommet O s’appuyant sur la polhodie, qui est dans ce cas un petit ovale entourant l’axe Ox 轢^s (ou Oz 轢^s), et par suite ^sg reste voisin de 諸 ゎ^s, et ゎ^s reste voisin de ゎ^g . Il n’en est pas de même si la perturbation s’exerce sur une rotation autour de Oy 轢^s; car, dans ce cas, l’axoïde lié au solide est défini par une polhodie qui longe les ellipses limites, ou se situe sur une demi-ellipse limite (fig. 1).

Dans le cas où A = B C, on voit que la réponse est affirmative si l’axe Ou 轢^s est Oz 轢^s, et qu’elle est négative si Ou 轢^s est perpendiculaire à Oz 轢^s.

Précisons la formulation des énoncés précédents: le fait que les axes Ou 轢^s et Ou 轢^g sont voisins doit être exprimé en majorant leur angle géométrique (c’est-à-dire à valeur dans [0, 神]); le fait que ^sg est voisin de 諸 ゎ^s doit être exprimé en majorant | ^sg 漣 諸 ゎ^s|. Ainsi, soit la propriété suivante: quel que soit 見 礪 0, on peut lui associer 兀 礪 0 tel que les inégalités:

vérifiées à la date t ¹, assurent pour t 閭 t ¹:

On exprime cette propriété en disant que les rotations uniformes correspondantes sont stables. L’instabilité consiste dans la négation de cette propriété.

2. Mouvement stationnaire

Soit encore un solide (S) à point fixé ^s = O^g = O, dont on désigne par Ox 轢^s, Oy 轢^s, Oz 轢^s les axes principaux d’inertie en O (les moments d’inertie respectifs sont: A, A, C) et dont le centre d’inertie G, situé sur Oz 轢^s, est défini par OG漣 l ん ^s. Supposons ce solide soumis uniquement aux efforts de pesanteur et à des efforts de liaison de moment en O négligeable. Dans ces conditions, les trois intégrales premières suivantes peuvent être écrites ( 切, , 﨏 étant les angles d’Euler usuels):

cependant que l’équation du moment par rapport à l’axe nodal:

montre qu’un mouvement à constant ( = ⁰ de sinus non nul, faute de quoi les angles d’Euler ne sont plus adéquats) est possible si l’égalité:

est vérifiée. Il en résulte que 切 reste constant et égal à 切 ⁰ et que 﨏 reste constant et égal à 﨏 ⁰ (utilisation des intégrales premières à constantes et r ⁰). Ainsi, dans cet exemple à trois paramètres de configuration, un paramètre reste constant et les deux autres, 切 et 﨏, sont des fonctions du premier degré par rapport au temps (mouvement stationnaire), et l’on a:

Mais, d’une part, l’égalité stricte écrite ci-dessus et qui relie les constantes de l’appareil (m, l, C, A), l’accélération g due à la pesanteur et les valeurs initiales ⁰, 﨏 ⁰ et 切 ⁰, ainsi que la condition rigoureuse ⁰ = 0, n’ont aucune chance d’être vérifiées exactement; et il existera toujours (quel que soit le soin expérimental apporté) une différence entre la valeur de mgl et celle du second membre; cela impose l’étude de la stabilité de ce mouvement stationnaire. D’autre part, l’expérience (rotation stationnaire possible d’une toupie, étudiée dans l’article GYROSCOPES, rotation impossible d’un crayon autour de sa pointe) nous montre que cette étude n’est pas sans objet et que la stabilité est sûrement conditionnée par une ou plusieurs inégalités entre les constantes de l’appareil et les valeurs initiales; en particulier, 﨏 ⁰ doit être assez grand .

Un tel état de fait amène à distinguer les valeurs initiales (q ⁰, q ⁰) effectivement réalisées des valeurs (q^e , q ^e ) strictement exigées par les conditions d’équilibre (q ^e = 0) ou de mouvement stationnaire. Par exemple, dans ce qui précède:

Citons une importante propriété. Quel que soit 見 礪 0, on peut lui associer 兀 礪 0 tel que les inégalités:

vérifiées à la date t ⁰ assurent pour t 閭 t ⁰:

On exprime cette propriété en disant que le mouvement stationnaire (théorique) défini par ( ^e , 切 ^e , 﨏 ^e ) est stable. L’instabilité consiste dans la négation de cette propriété.

3. Exemple issu de la dynamique des systèmes (équilibre)

Soit un solide (S¹) en mouvement rotoïde d’axe Oz(horizontal) par rapport au galiléen: le centre d’inertie G¹ de ce solide est défini par OG 轢¹ = a ¹ size=1^ゑ1 (fig. 2). Un point A lié à (S¹) est défini par OA= a ゑ ¹, avec a 礪 a ¹; en ce point passe Azqui est l’axe d’un rotoïde entre un deuxième solide (S²) et le solide (S¹). L’axe Ax 轢² est lié à (S²): sur cet axe, un point B lié à (S²) est défini par AB= l ゑ ², et le centre d’inertie G² de (S²) est défini par AG 轢² = 漣 b ゑ ², avec b 礪 0. L’axe Oyest la verticale ascendante de O, le point B est assujetti à rester dans le plan Oyz . Toutes les liaisons mises en jeu développent une puissance négligeable. Étudier la stabilité de l’équilibre dans lequel l’angle = (Ox 轢, OA 轢) prend la valeur 神/2 et dans lequel l’angle ( を, ゑ²) = 廓 prend la valeur nulle est un problème qui a été résolu de manière plus simple (cf. DYNAMIQUE, chap. 9 et le théorème de Lejeune-Dirichlet, infra , chap. 4).

Les angles et 廓 ne sont pas indépendants, mais ils ont entre eux la relation:

De plus, on a:

d’où l’on déduit:

Par suite, la puissance développée par les torseurs de pesanteur est:

d’où la fonction de force:

Pour le voisinage de la position étudiée ( = 神/2, 廓 = 0), on peut écrire:

donc, dans ces conditions,

Pour 﨎 = 0, la fonction U prend la valeur:

et le calcul de la partie principale (U 漣 U⁰) de U 漣 U⁰ en fonction de l’infiniment petit principal 﨎 fournit le résultat suivant:

ce qui signifie que U est extremum pour 﨎 = 0; il y a équilibre. Mais l’extremum peut être respectivement un maximum ou un minimum si:

Le théorème de Lejeune-Dirichlet permet d’affirmer que si U est maximum pour 﨎 = 0 (c’est-à-dire = 神/2), alors l’équilibre de l’ensemble est stable, c’est-à-dire que, quel que soit 見 礪 0, on peut lui associer 兀 礪 0 tel que les inégalités:

vérifiées au temps t ⁰, assurent pour t 閭 t ⁰:

Dans les conditions précédentes, 諸 est une variable d’homogénéité ayant la dimension physique d’une vitesse angulaire de manière que 兀 soit un nombre pur. Cette intervention est toujours possible et, dans la discussion de la stabilité, quand on écrit q et sa dérivée q par rapport au temps, on suppose que, par suite d’intervention implicite de variables d’homogénéité, q et q sont dénués de dimension physique.

4. Définition générale de la stabilité

Moyennant la convention précédente, on allégera l’écriture en traitant comme un tout la configuration (q ) et l’état de vitesse (q ), on notera donc s l’élément (q ¹, ..., qⁿ ; q ¹, ..., q ⁿ ) de R²ⁿ et s^e l’élément [(q ¹)^e , ..., (qⁿ )^e ; 0, ..., 0], et on appelera voisinage de s^e dans R²ⁿ tout ensemble contenant une boule de centre s^e de rayon 福 non nul.

La stabilité de l’équilibre s^e consiste dans la propriété suivante: Quel que soit V, voisinage de s^e , on peut lui associer W, voisinage de s^e , tel que l’hypothèse s ⁰ 捻 W implique:

L’instabilité consiste dans la négation de cette propriété. Si l’ensemble mécanique étudié est à liaisons indépendantes du temps, la stabilité éventuelle de la position d’équilibre définie par la valeur q^e de q est une propriété indépendante du choix des paramètres; la propriété ci-dessus énoncée sert donc également dans le cas du mouvement stationnaire (cf. chap. 2), ainsi que dans l’exemple du chapitre 1 où les 諸^j sont constants.

Compte tenu de cette définition précise de la stabilité, on peut choisir 見 礪 0, arbitrairement petit, mais qui reste fixé dans la discussion de la stabilité de q^e = 0, laquelle requiert seulement l’étude des mouvements sur un intervalle de temps tel que |q (t )| 諒 見.

On exploite souvent cette remarque en choisissant 見 si petit que les fonctions de q à faire intervenir dans l’étude puissent être remplacées par des développements limités. Ainsi, on remplace les équations du mouvement par d’autres qui semblent «voisines» et plus simples, notamment linéaires. Une telle linéarisation ne constitue pas une méthode mathématique rigoureuse pour juger de la stabilité. Le fait de remplacer un système différentiel par un autre, même voisin, peut modifier considérablement le comportement des solutions. On dira tout au plus qu’on a associé des oscillateurs linéaires au mouvement stationnaire étudié. Les techniques de linéarisation sont très employées en pratique; elles sont souvent les seules disponibles et ne faisant pas appel à un développement mathématique considérable. À ce sujet, le chapitre 6 de cet article permettra de comparer les difficultés de l’étude analytique, suivant qu’on suit une méthode de linéarisation ou une méthode mathématique plus rigoureuse qui va maintenant être exposée. Auparavant, dans le cadre des résultats élémentaires, rappelons l’énoncé du théorème (très commode) de Lejeune-Dirichlet :

«Si un ensemble mécanique (D) est à liaisons indépendantes du temps et si ses mouvements sont régis notamment par l’intégrale première de l’énergie (cf. DYNAMIQUE, chap. 7):

en un point q^e pour lequel la fonction U présente un maximum local strict, l’équilibre éventuel dans la configuration correspondante est stable (condition suffisante d’équilibre, mais qui n’est nullement nécessaire).»

Cela nous permet de répondre à la question posée au chapitre précédent. Si:

la configuration définie par = 神/2 est stable.

5. La méthode de Liapounoff

Considérons le système différentiel:

où x décrit un espace vectoriel réel à n dimensions et f est une application à valeurs dans cet espace, t étant une variable réelle. On suppose de plus que f (x , t ) satisfait à la condition de Lipschitz:

avec t 捻 [t ⁰, t ⁰ + T] et où k est une constante dans le domaine 行(a , 精):

et on suppose aussi que f (0, t ) = 0 quel que soit t . On voit ainsi que x = 0 est un point critique; on se propose d’en discuter la stabilité suivant les idées introduites par Liapounoff.

Si V(x , t ) est une fonction à valeurs scalaires, pourvue de dérivées partielles premières continues dans 行(a , 精 ), l’étude de sa variation le long d’une trajectoire ( 臨), définie par x = x (t ) solution du système différentiel, peut aisément se faire en étudiant le signe de:

où dans le second membre les xⁱ devront être remplacés par les composantes xⁱ (t ) de la solution considérée.

On dira que la fonction V(x , t ) a un signe constant si, dans un domaine 行(a , 精) convenable, elle est différentiable, si elle ne prend que des valeurs d’un même signe ou si elle est nulle, et si V(0, t ) = 0. Elle sera dite positive ou négative selon la nature de ce signe.

Si W(x ) est une fonction indépendante du temps, on dira que W est définie positive (ou définie négative) si elle est différentiable et positive (ou négative) dans un 行(a ) convenable et si elle ne s’annule qu’à l’origine.

La fonction V(x , t ) sera dite définie positive (ou définie négative) s’il existe une fonction définie positive W(x ) telle que V 漣 W (ou 漣 [V 漣 W]) est positive dans un 行(a , 精) et si V(0, t ) = 0.

Premier théorème de Liapounoff. Si, pour le système différentiel, il existe une fonction définie V(x , t ) dont la dérivée d V/dt est d’un signe constant opposé à celui de V, alors x = 0 est une solution stable du système.

Deuxième théorème de Liapounoff. Si, pour le système différentiel, et dans un domaine 行(a , 精), les fonctions V(x , t ) et V (x , t ) sont définies et de signes contraires, et si V(x , t ) tend vers 0 quand x0 uniformément par rapport à t , alors x = 0 est une solution asymptotiquement stable de ce système.

Troisième théorème de Liapounoff. Si, pour le système différentiel, on a pu construire une fonction V(x , t ) tendant vers 0 quand x0 uniformément par rapport à t , telle que V (x , t ) est définie (positive ou négative) dans 行(a , 精) et que, pour chaque valeur t 閭 精 et pour chaque valeur de 兀 positif choisi aussi petit qu’on veut, V peut prendre dans 瑩x 瑩 麗 兀 le signe de V , alors l’origine est instable pour le système différentiel.

Théorème de Tchetaev. Considérant le système dx/dt = f (x ), on suppose connue une fonction V(x ) telle que:

1. V(x ) et V (x ) = f (x ) 練 grad V sont positifs dans 行¹, sous-ensemble de la boule 瑩x 瑩 諒 a ;

2. V(x ) = 0 sur 行 漣¹ 惡 行 漣², où 行² désigne le complémentaire de 行¹ dans 瑩x 瑩 諒 a , où 行 漣¹ et 行 漣² sont les fermetures respectives de 行¹ et 行²;

3. x = 0 appartient à 行 漣¹ 惡 行 漣² et f (0) = 0.

En conclusion, x = 0 est une solution instable de dx/dt = f (x ).

6. Exemples de stabilité

Stabilité de la rotation autour d’un axe principal d’un solide mobile autour de son centre d’inertie

Les équations du mouvement, dans les notations classiques, sont:

A, B, et C désignent les moments principaux d’inertie, et p , q et r les composantes sur les axes principaux de la rotation instantanée du solide.

Étudions la stabilité de la solution: p = 0, q = 0 et r = r ⁰ 礪 0.

Introduisons les nouvelles variables 﨡, 兀 et 﨣:

On obtient le système:

Si A 閭 B 礪 C, nous prendrons:

définie positive; on vérifie que V = 0 et, par le premier théorème de Liapounoff, on peut en déduire la stabilité de la solution 﨡 = 兀 = 﨣 = 0.

Si A 諒 B 麗 C, nous prendrons:

définie négative, telle encore que V = 0; il y a donc stabilité en vertu du premier théorème de Liapounoff.

Enfin, si A 麗 C 麗 B, nous prendrons V = 﨡 練 兀 dont la dérivée est:

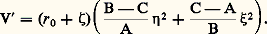
Par le théorème de Tchetaev, on reconnaît qu’il y a instabilité.

Dans la technique de linéarisation, on aurait écrit directement:

C’est-à-dire que, par élimination de 﨡 ou de 兀, on obtient l’équation du second ordre:

(avec 﨎 = 﨡 ou 兀), qui ne s’écrit sous la forme 﨎 + 行² 﨎 = 0 (oscillateur stable) que si (C 漣 A)(C 漣 B) 礪 0, c’est-à-dire si C est le plus petit ou le plus grand des trois moments d’inertie principaux.

Oscillateurs linéaires associés aux mouvements «voisins» du mouvement stationnaire d’un ensemble mécanique

Reprenons l’étude commencée au chapitre 2 et engageons la linéarisation des équations. Si nous calculons 切 et 﨏 à l’aide des deux intégrales premières linéaires en 切 et 﨏 et si nous reportons le résultat dans l’équation du moment nodal, nous trouvons une équation différentielle du second ordre en qui est valable dans tous les cas de mouvement:

Pour un mouvement stationnaire, on doit avoir:

c’est-à-dire que, avec C²r ²⁰ 礪 Amgl cos ^e , il existe deux valeurs de 切 ^e pour lesquelles reste constant. On établit l’équation de l’oscillateur linéaire associé aux mouvements voisins de ce mouvement stationnaire. À cet effet, on pose = ^e + 﨎 et on obtient:

qui est de la forme 﨎 + 行² 﨎 = 0, sous la réserve que:

Cette condition est celle de la stabilité de l’oscillateur associé aux mouvements «voisins» du mouvement stationnaire étudié. La mise en évidence générale des oscillateurs associés à un équilibre ou à un mouvement stationnaire ainsi que l’étude de leur stabilité constituent l’objet de l’article VIBRATIONS MÉCANIQUES.

• XII^e; lat. stabilitas

1 ♦ Caractère de ce qui tend à demeurer dans le même état. ⇒ constance, continuité, fermeté, permanence. La stabilité des institutions anglaises. « la stabilité numérique d'une population animale [...] suggère l'existence de systèmes régulateurs » (J. Hamburger). — Stabilité de la monnaie, des cours. ⇒ fermeté. Compromettre la stabilité : déstabiliser.

2 ♦ (1549) État d'une construction capable de demeurer dans un équilibre permanent, sans ruptures ni tassements, et de résister à des contraintes normales. ⇒ aplomb, équilibre. « ces massifs piliers donnent [...] une ferme assiette et une stabilité extraordinaire au vaisseau de la cathédrale » (Gautier).

3 ♦ (1845) Propriété d'un corps de revenir à sa position d'équilibre et de reprendre son mouvement après une modification passagère. Stabilité d'un avion, d'un véhicule.

4 ♦ Phys. Propriété d'un système qui demeure dans un état d'équilibre ou de régime permanent. Stabilité de fréquence d'un émetteur. « Les mésons joueraient un rôle important dans cette stabilité des noyaux » (Broglie).

♢ Chim. État d'une molécule qui ne subit aucune transformation spontanée.

5 ♦ Automat. Aptitude d'un système bouclé à ne pas osciller. Critère de stabilité. — Aptitude d'un système automatique à atteindre sa position d'équilibre avec un minimum d'oscillations.

Synonymes :

Contraires :

Synonymes :

Contraires :

Contraires :

n. f.

d1./d Qualité de ce qui est stable, solide. Stabilité d'un édifice.

|| Fig. Qualité de ce qui est durable, bien assis. La stabilité des institutions.

d2./d Suite dans les idées, constance. Un esprit qui manque de stabilité.

d3./d PHYS, CHIM Caractéristique d'un système en état d'équilibre stable.

⇒STABILITÉ, subst. fém.

Caractère, qualité de ce qui est stable ou en équilibre stable. Anton. instabilité.

A. — 1. Caractère de ce qui reste en place, sans bouger ni tomber. Pied de grandes dimensions assurant une parfaite stabilité (Catal. instrum. lab. (Prolabo), 1932, p. 128). Avant de s'asseoir (...) M. Élie vérifia la stabilité de sa chaise (MONTHERL., Célibataires, 1934, p. 740).

— [Avec une idée de solidité notamment dans le domaine de l'archit., de la constr., des trav. publ.] ,,État d'une construction qui demeure en bon état d'équilibre, sans rupture ni tassement des matériaux qui la composent`` (VOGÜÉ-NEUFVILLE 1971). Stabilité d'un édifice, d'un mur, d'une chaussée; lois de stabilité et de cohésion des matériaux; augmenter par des contreforts la stabilité d'une paroi. Mais il y a [en architecture] deux genres de solidité, la pesanteur et la cohésion. La solidité par la pesanteur s'appelle stabilité (Ch. BLANC, Gramm. arts dessin, 1876, p. 113):

• 1. Il s'agit là d'utiliser pour la confection de la chaussée — ou tout au moins de sa fondation — le sol naturel lui-même, s'il s'y prête, en améliorant ses propriétés par l'addition des éléments qui lui manquent pour lui conférer une stabilité et une résistance suffisantes: addition de sable à un terrain argileux ou d'argile à un terrain sableux, incorporation de ciment ou de bitume, etc.

J. THOMAS, Route, 1951, p. 317.

a) MÉCAN. ,,Tendance d'un système à demeurer dans un état d'équilibre ou de régime permanent`` (MATHIEU-KASTLER Phys. 1983). Stabilité de l'équilibre; stabilité dynamique; stabilité négative, positive. Les conditions de stabilité s'expriment par des propositions importantes (MATHIEU-KASTLER Phys. 1983).

b) MOYENS DE TRANSP. [À propos d'un navire] Faculté de conserver un cap constant sans qu'il soit nécessaire à l'homme de barre de manœuvrer fréquemment le gouvernail. [Le cuirassé] représentait le type de bâtiment de combat individuellement le plus puissant en raison (...) de sa vitesse (...), de sa flottabilité et de sa stabilité, qui étaient aussi grandes que possible (LE MASSON, Mar., 1951, p. 15). [À propos d'un aéronef] Capacité d'un aéronef à retrouver une assiette de vol normale après une modification inopinée (d'apr. THIES Aéromodélisme 1984). Le pilote fait des embardées et ne gouverne pas régulièrement au cap donné, surtout si la stabilité de route de l'aéronef est mauvaise (A.-B. DUVAL, HÉBRARD, Nav. aér., 1928, p. 49). [À propos d'une automob.] Bonne tenue de route. Par qualité des pneus il faut d'ailleurs entendre aussi bien la résistance à l'usure et aux fatigues de toutes sortes que leur impose la route, l'adhérence au sol, les caractéristiques qui donnent aux véhicules leur stabilité, que le silence et le confort (TINARD, Automob., 1951, p. 344). [À propos de véhicules ferroviaires] ,,Ensemble des phénomènes accompagnant la circulation des véhicules ferroviaires et ne présentant pas de caractère oscillatoire entretenu`` (Lar. encyclop. Suppl. 1975).

B. — [Avec une idée d'absence de variation]

1. [Dans le temps]

a) Capacité à conserver ses caractéristiques initiales, à ne pas subir de transformations plus ou moins spontanées. La conception évolutionniste de Lamarck (...) suppose que celles-ci [les espèces] passent de l'une à l'autre et qu'elles n'ont pas été l'objet de créations individuelles. L'espèce possède une stabilité provisoire en rapport avec la stabilité du milieu (Hist. gén. sc., t. 3, vol. 1, 1961, p. 542).

b) Spécialement

— AGRIC., GÉOL. Stabilité (d'un sol). Capacité de résister à l'action des agents de dégradation. La couverture herbacée accroît la stabilité structurale du sol et freine efficacement l'érosion (BOULAY, Arboric. et prod. fruit., 1961, p. 93).

— CHIM. Propriété d'un corps, d'un composé, qui est dans son domaine d'équilibre et ne peut être le siège d'aucune réaction spontanée (d'apr. DUVAL 1959). Au point de vue chimique, la stabilité de l'arsenic dans le stovarsol [produit pharmaceutique] est grande. On peut chauffer impunément à l'ébullition des solutions neutres légèrement acides ou légèrement alcalines (Ce que la Fr. a apporté à la méd., 1946 [1943], p. 74). Si nous envisageons la série des ions et la stabilité des assemblages qu'ils forment, celle-ci décroît à mesure que le diamètre de l'ion croît et que la valence décroît. Le tétraèdre constitué par l'aluminium et plus encore par le fer ferrique est beaucoup moins stable que celui constitué par le silicium (CAILLÈRE, HÉNIN, Minér. argiles, 1963, p. 32).

Stabilité d'une suspension. Capacité d'une suspension à rester semblable à elle-même sans décantation, sinon lente, des particules. La méthode [des mesures de densités], si elle est d'un emploi commode, fait l'objet d'une critique assez sérieuse: elle est très sensible à la stabilité de la suspension (CAILLÈRE, HÉNIN, Minér. argiles, 1963, p. 81).

— INDUSTR. AGRO-ALIM. Propriété d'une denrée à résister à l'action de facteurs extérieurs qui pourraient la faire évoluer. La stabilité est un des composants essentiels de la qualité des denrées (CLÉM. Alim. 1978).

— PÉTROCHIM. Qualité d'un produit pétrolier qui ne s'altère pas en cours de stockage ou d'utilisation. Éprouvette graduée bouchée émeri (...) pour le contrôle de la stabilité au stockage des émulsions bitumineuses pour routes (Catal. instrum. lab. (Prolabo), 1932, p. 238). La stabilité des essences exige des inhibiteurs contre la formation de gommes; celle des lampants et des huiles de graissage concerne avant tout la couleur, qui ne doit pas devenir plus foncée avec le temps (Lar. encyclop.).

— PYROTECHNIE. Résistance d'une substance explosive à s'altérer spontanément. La stabilité ne peut être précisée que dans des conditions définies (Pyrotechnie 1972). Les épreuves de stabilité (...) « épreuve de résistance à 110 C », ont pour objet d'évaluer le degré de stabilité de ces substances, soit à la fin de leur fabrication, soit au cours de leur conservation (GDEL).

— PHYS. NUCL. Capacité à ne pas se désintégrer spontanément; fait de ne pas présenter de radioactivité mesurable. Les premières connaissances sur la stabilité des atomes ont été obtenues alors que la notion de noyau n'existait pas encore (...) la stabilité nucléaire exige un certain rapport entre la charge et la masse du noyau (JOLIOT, CURIE, Radioact. artif., 1935, p. 3).

2. [Dans l'espace; avec une idée d'immobilité, de sédentarité]

a) [À propos d'une pers.] Fait de ne pas être mobile, de ne pas changer constamment ou fréquemment de lieu de résidence. Le chef d'entreprise (...) devrait bien méditer sur les avantages multiples que peut lui conférer la création d'équipes sportives dans son personnel: rendement accru de la production, esprit de communauté, stabilité de la main-d'œuvre (BECQUET, Organ. loisirs travaill., 1939, p. 69).

— En partic. Fait de garder un même emploi. Stabilité professionnelle. Politique des anciennes compagnies de chemin de fer payant à leur personnel des salaires relativement faibles mais leur assurant en contre partie une parfaite stabilité d'emploi et d'importants avantages complémentaires (MEYNAUD, Groupes pression en Fr., 1958, p. 262). Quand on discute de l'amélioration de la situation des chercheurs dans le sens d'une amélioration de la stabilité, on se heurte toujours à cette crainte que la fécondité du chercheur ne s'épuise rapidement avec l'âge (Encyclop. éduc., 1960, p 267).

b) [À propos d'un inanimé] Caractère de ce qui ne bouge pas, qui se maintient dans la durée. Le magicien est censé pouvoir procurer à ses clients la richesse, la santé. Les rites religieux peuvent aussi avoir cet effet, selon la croyance des fidèles, ou bien ils contribuent à la stabilité du monde, à la prolifération des espèces animales, ils assurent de bonnes récoltes (Jeux et sports, 1967, p. 802).

— MUS., HARM. ,,Propriété qu'à une note ou un accord de créer une impression statique de repos`` (Mus. 1976). [Les] compositeurs modernes (...) se trompent parfois, faute de bien connaître les conditions de stabilité de l'édifice harmonique qu'ils construisent (DURUTTE, Esthét. mus., 1876, p. 353).

1. [À propos d'une pers.] Constance dans la conduite, les idées, les choix. Conférer, donner de la stabilité (à qqn). Maze a raison; ces femmes qui n'ont pas de sens manquent de stabilité, même dans l'intelligence. Elles sont capricieuses et décevantes (CHARDONNE, Épithal., 1921, p. 446).

— P. méton.

♦ [À propos d'un affect, d'un comportement] Synon. de permanence. Les rythmes psychiques: entre le changement pur qui ne ramènerait jamais un être au même état, et l'identité pure qui le maintiendrait absolument égal à lui-même, le rythme assure un certain retour, et par suite, une certaine stabilité dans le changement (MOUNIER, Traité caract., 1946, p. 281):

• 2. En pensant l'univers et en nous pensant nous-mêmes, nous engendrons un ordre de l'être intermédiaire entre l'instantanéité de l'être des corps et la permanence éternelle de Dieu. Pourtant, l'homme passe lui-même sous cette frêle stabilité de sa mémoire, qui va sombrer à son tour dans le néant si Dieu ne la recueille et ne la stabilise.

GILSON, Espr. philos. médiév., 1932, p. 184.

♦ [À propos des faits soc., des instit. soc.] La forme du mariage n'est pas tout; il faut encore se préoccuper de sa stabilité. Il y a à cet égard de grandes différences, entre les diverses sociétés humaines (Tiers Monde, 1956, p. 164). Le plus fréquemment, la religion se présente au sociologue comme une puissance de stabilité, de bon ordre moral et social, comme une norme doublant d'une référence divine les règles terrestres du bien-vivre (Univers écon. et soc., 1960, p. 64-9).

2. [À propos d'un inanimé]

a) Caractère de ce qui ne varie pas, de ce qui demeure au même niveau, à la même valeur. Le mot « dépôt » implique plus de stabilité que l'expression « compte courant », qui évoque l'idée d'un flux et d'un reflux, et admet la possibilité de soldes actifs ou passifs (BAUDHUIN, Crédit et banque, 1945, p. 165).

b) Spécialement

) ÉCON. [Avec une idée d'équilibre] Stabilité d'un marché, des cours (du pétrole, de la Bourse). Cet examen de la problématique des croissances liées aide à préciser liminairement la place qui revient à la théorie néo-classique dans l'interprétation des rapports entre stabilité financière et équilibre de la balance des paiements (PERROUX, Écon. XX^e s., 1964, p. 521).

♦ Stabilité du pouvoir d'achat. Maintien de la quantité de biens ou services que peut procurer une unité monétaire à un moment donné. Dans des périodes de hausse de prix inflationniste, la fonction sociale de l'impôt — celle du « nivellement » des revenus et fortunes — doit être reléguée au second plan pour des raisons relatives à la considération des buts économiques et monétaires (stabilité du pouvoir d'achat de la monnaie, équilibre des balances extérieures) (Univers écon. et soc., 1960, p. 48-1).

♦ Stabilité de la monnaie, stabilité monétaire (par rapport à une autre, à d'autres monnaies). Fait pour une monnaie de ne pas subir de tensions à la hausse ou à la baisse, de ne pas subir de dévaluation ou de réévaluation. Stabilité du dollar, du franc. Alors que les classiques limitaient le rôle de l'État à la protection de la stabilité de la monnaie et à la gestion équilibrée des finances publiques, Keynes accorde à l'État un rôle décisif dans toute l'activité économique (LESOURD, GÉRARD, Hist. écon., 1968, p. 172).

♦ Stabilité des prix. Fait pour les prix de ne pas subir de trop fortes augmentations. Les progrès sont supposés acquis seulement moyennant l'instabilité; la stabilité des quantités et celle des prix, la stabilité des prix et celle des changes sont considérées comme incompatibles entre elles (PERROUX, Écon. XX^e s., 1964, p. 570).

♦ Contrats de stabilité. ,,Accords passés entre les professions et les pouvoirs publics pour maintenir la stabilité des prix`` (GDEL).

) POL. [À propos d'un régime, d'une constitution] Caractère d'équilibre provenant de la pondération des pouvoirs, de ce qu'ils se contiennent mutuellement sans faire courir le risque de crise. La stabilité constitutionnelle, la puissance et la prospérité américaine ont valu à la Constitution américaine de nombreux admirateurs (VEDEL, Dr. constit., 1949, p. 167).

♦ Stabilité gouvernementale. ,,Caractéristique d'un régime parlementaire dans lequel les changements gouvernementaux sont peu fréquents`` (GDEL). Stabilité ministérielle. ,,Continuité dans les titulaires de certains postes ministériels, même en cas d'instabilité gouvernementale`` (GDEL). Quant aux effets de l'existence du cabinet sur la hiérarchie classique et sur les relations entre l'administration centrale et le ministre, ils sont, à l'évidence, différents en période d'instabilité ou de stabilité ministérielle (BELORGEY, Gouvern. et admin. Fr., 1967, p. 91).

— [Dans le cont. des relations internat.] L'arme nucléaire introduit un facteur de stabilité absolument nouveau. Là où son action se fait sentir, les situations se figent, alors que, là où elle est absente, le bouleversement s'accélère (BEAUFRE, Dissuasion et strat., 1964, p. 203).

c) P. anal., MÉTÉOR. Stabilité (hydrostatique). ,,État d'équilibre hydrostatique de l'atmosphère dans lequel une particule d'air écartée légèrement de son niveau initial est soumise à une force hydrostatique tendant à l'y ramener`` (VILLEN. 1974). Stabilité de l'atmosphère; zone de stabilité; stabilité absolue. Les régions d'entropie croissante sont des régions de stabilité (DELC. 1926). Quand il y a dans l'atmosphère une inversion de température, cette inversion (...) donne une grande stabilité à la couche correspondante (MAURAIN, Météor., 1950, p. 120).

Prononc. et Orth.: [stabilite]. Att. ds Ac. dep. 1694. Étymol. et Hist. 1. a) 1119 stabilitet « qualité de ce qui a une assiette ferme » (PHILIPPE DE THAON, Comput, 983 ds T.-L.); b) 1832 « propriété d'un corps de revenir à son équilibre après de petites oscillations » (RAYMOND); c) 1862 aéron. (Presse sc. des Deux Mondes, II, 118 ds R. Ling. rom. t. 47, p. 202); 2. a) fin XII^e s. « fermeté, constance (de l'esprit, des sentiments) » (Règle de S. Benoit, ms. Sens, p. 162 ds GDF. Compl.); b) 1406 « qualité de ce qui est durable (en parlant de la foi) » (Ord. [4 oct.], IX, 148, ibid.); 3. 1818 chim. (THENARD, Instit. Méd. acad. sc., t. 3, p. 444 ds LITTRÉ). Empr. au lat. stabilitas « solidité, fermeté, constance », dér. de stabilis (stable). A remplacé l'a. fr. estabilité (1^re moit. du XII^e s., estabilited, Psautier Oxford, 103, 6 ds T.-L.; 1121-34, estabilité, PHILIPPE DE THAON, Bestiaire, éd. E. Walberg, 1509 et 2786). Fréq. abs. littér.: 360. Fréq. rel. littér.:XIX^e s.: a) 468, b) 333; XX^e s.: a) 339, b) 748. Bbg. DUB. Pol. 1962, p. 426. — QUEM. DDL t. 11, 21, 28. — VARDAR Soc. pol. 1973 [1970], p. 310.

stabilité [stabilite] n. f.

ÉTYM. V. 1119; lat. stabilitas, de stabilis. → Stable.

❖

1 Caractère de ce qui tend à demeurer dans le même état. ⇒ Stable; assiette, certitude (infra cit. 4), consistance, constance, continuité, équilibre, fermeté, permanence, solidité. || Stabilité des institutions. || La stabilité politique, de la vie politique. || Stabilité gouvernementale, ministérielle. || Des illusions de stabilité, de durée (→ Finir, cit. 16). || La stabilité des convictions, des habitudes (→ Destruction, cit. 3), de l'attention (→ Exorde, cit. 3), des sentiments. ⇒ Calme, équilibre. — Vieilli. || La stabilité d'une personne (→ Inconstance, cit. 11).