- ЖИДКОСТЬ
-
агрегатное состояние в-ва, промежуточное между твёрдым и газообразным. Ж. присущи нек-рые черты твёрдого тела (сохраняет свой объём, образует поверхность, обладает определ. прочностью на разрыв) и газа (принимает форму сосуда, в к-ром находится, может непрерывно переходить в газ); в то же время она обладает рядом только ей присущих особенностей, из к-рых наиб. характерная — текучесть.По хим. составу различают однокомпонентные, или чистые, Ж. и двух- или многокомпонентные жидкие смеси (р-ры). По физ. природе Ж. делятся на нормальные (обычные) Ж., жидкие кристаллы с сильно выраженной анизотропией и квантовые жидкости (жидкие 4Не, 3Не и их р-ры). Нормальные чистые Ж. имеют только одну жидкую фазу, 4Не может находиться в двух жидких фазах — нормальной и сверхтекучей, 3Не — в нормальной и двух сверхтекучих, а жидкокрист. в-ва — в нормальной и одной или даже неск. анизотропных фазах.Норм. Ж. макроскопически однородны и изотропны при отсутствии внеш. воздействий. Эти св-ва сближают Ж. с газами, но резко отличают их от анизотропных крист. тв. тел. Аморфные тв. тела (напр., стёкла) явл. переохлаждёнными Ж. (см. АМОРФНОЕ СОСТОЯНИЕ) и отличаются от обычных Ж. существенно большей вязкостью и числ. значениями кинетич. хар-к.Область существования нормальной жидкой фазы для чистых Ж., жидкого 4Не и жидких кристаллов ограничена со стороны низких темп-р Т фазовыми переходами соотв. в твёрдое (кристаллизацией), сверхтекучее и жидко-анизотропное состояние. При давлениях р ниже критич. давления рк нормальная жидкая фаза ограничена со стороны высоких Т фазовым переходом в газообразное состояние — испарением. При давлениях р>рк фазовый переход отсутствует и по физ. св-вам Ж. в этой области неотличима от плотного газа. Наивысшая темп-ра Тк, при к-рой ещё возможен фазовый переход жидкость — газ, наз. критической. Значения рк и Тк определяют критич. точку чистой Ж., в к-рой св-ва Ж. и газа становятся тождественными. Наличие критич. точки для фазового перехода жидкость — газ позволяет осуществить непрерывный переход из жидкого состояния в газообразное, минуя область, где газ и Ж. сосуществуют (см. КРИТИЧЕСКОЕ СОСТОЯНИЕ).При нагревании или уменьшении плотности св-ва Ж. (теплопроводность, вязкость, самодиффузия и др.), как правило, меняются в сторону сближения со св-вами газов. Вблизи же темп-ры кристаллизации большинство св-в норм. Ж. (плотность, сжимаемость, теплоёмкость, электропроводность и др.) близки к таким же св-вам соответствующих тв. тел. Ниже приведены значения теплоёмкости (в Дж/кг•К) при пост. давлении (ср) нек-рых в-в в твёрдом и жидком состояниях при темп-ре кристаллизации: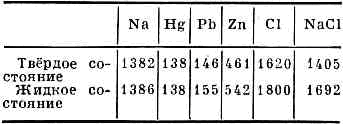 Малое различие этих теплоёмкостей показывает, что тепловое движение в Ж. и тв. телах вблизи темп-ры кристаллизации имеет примерно одинаковый хар-р.Наличие сильного межмолекулярного взаимодействия обусловливает существование поверхностного натяжения на границе Ж. с любой другой средой. Влияние поверхностного натяжения на равновесие и движение свободной поверхности Ж., границ Ж. с тв. телами или границ между несмешивающимися Ж. относится к области капиллярных явлений.Характерная величина, определяющая фазовое состояние в-ва, e(Т, р) — отношение ср. потенц. энергии вз-ствия молекул к их ср. кинетич. энергии, зависящее от Т и р. Для Ж. e(Т, р)=1, это означает, что интенсивности упорядочивающих межмол. вз-ствий и разупорядочивающего теплового движения молекул имеют сравнимые значения, чем и определяется вся специфичность жидкого состояния в-ва (для тв. тел e(T, р)->1, для газов e(T, р)-1). Тепловое движение молекул Ж. состоит из сочетания коллективных колебат. движений того же типа, что и в крист. телах, и происходящих время от времени скачков молекул из одних временных положений равновесия (центров колебаний) в другие. Каждый скачок происходит при сообщении молекуле энергии активации, достаточной для разрыва её связей с окружающими молекулами и перехода в окружение др. молекул. В результате большого числа таких скачков молекулы Ж. более или менее быстро перемешиваются (происходит самодиффузия, к-рую можно наблюдать, напр., методом меченых атомов). Характерные частоты скачков составляют 1011 — 1012 с-1 для низкомол. Ж., много меньше — для высокомолекулярных, а в отд. случаях, напр. для сильновязких Ж. и стёкол, могут оказаться чрезвычайно низкими.Колебат. часть теплового движения ч-ц Ж. может быть описана с помощью набора дебаевских волн, к-рые могут проявляться в спектрах Мандельштама — Бриллюэна рассеяния и рассеяния нейтронов. Неупорядоченная часть движения молекул, связанная гл. обр. с тепловым трансляц. движением, проявляется в спектрах рассеянных жидкостью пучков света или нейтронов в виде дополнительной несмещённой довольно интенсивной компоненты, отсутствующей у кристаллов. Термодинамич. теория рассеяния света объясняет её как результат рассеяния света на флуктуациях энтропии. Изучение спектров рассеянных света и нейтронов явл. мощным инструментом исследования поляризационных и др. коллективных движений в Ж.При наличии внеш. силы, сохраняющей своё направление более длит. время, чем интервалы между скачками, молекулы перемещаются в ср. в направлении этой силы. Т. о., статич. или НЧ механич. воздействия приводят к проявлению текучести Ж. как суммарному эффекту от большого числа мол. переходов между временными положениями равновесия. При частоте воздействий, превышающей характерные частоты мол. скачков, у Ж. наблюдаются упругие эффекты (напр., сдвиговая упругость), типичные для тв. тел.В рамках мол. теории однородность и изотропность нормальных Ж. объясняется отсутствием у них дальнего порядка во взаимных положениях и ориентациях молекул (см. ДАЛЬНИЙ И БЛИЖНИЙ ПОРЯДОК). Положения и ориентации двух или более молекул, расположенных далеко друг от друга, оказываются статистически независимыми. В жидких кристаллах дальний порядок наблюдается лишь в ориентации молекул, но отсутствует в расположении их центров масс.Ж. иногда разделяют на неассоциированные и ассоциированные, в соответствии с простотой или сложностью их термодинамич. св-в. Предполагается, что в ассоциированных Ж. есть сравнительно устойчивые группы молекул — комплексы, проявляющие себя как одно целое. Существование подобных комплексов в нек-рых р-рах доказывается прямыми физ. методами. Наличие устойчивых ассоциаций молекул в однокомпонентных Ж. недостоверно.Основой совр. мол. теорий жидкого состояния послужило эксперим. обнаружение методами рентгеновского структурного анализа и нейтронографии ближнего порядка в Ж.— согласования (корреляции) во взаимных положениях и ориентациях близко расположенных групп, состоящих из двух, трёх и большего числа молекул. Эти статистич. корреляции, определяющие мол. структуру жидкости, простираются на область протяжённостью порядка неск. межат. расстояний и исчезают для далеко расположенных друг от друга ч-ц (отсутствие дальнего порядка).По структуре и способам описания Ж. делят на простые и сложные. К первому классу относят однокомпонентные атомарные жидкости (жидкие чистые металлы, сжиженные инертные газы и, с нек-рыми оговорками, Ж. с малоат. симметричными молекулами, напр. ССl4). Для описания их св-в достаточно указать взаимное расположение атомов. Для простых Ж. результаты рентгеноструктурного или нейтронографич. анализа могут быть выражены с помощью т. н. радиальной функции распределения g(r) (рис.). Эта ф-ция характеризует распределение ч-ц вблизи произвольно выбранной ч-цы, т. к. значения g(r) пропорц. вероятности нахождения двух ч-ц на нек-ром заданном расстоянии r друг от друга.
Малое различие этих теплоёмкостей показывает, что тепловое движение в Ж. и тв. телах вблизи темп-ры кристаллизации имеет примерно одинаковый хар-р.Наличие сильного межмолекулярного взаимодействия обусловливает существование поверхностного натяжения на границе Ж. с любой другой средой. Влияние поверхностного натяжения на равновесие и движение свободной поверхности Ж., границ Ж. с тв. телами или границ между несмешивающимися Ж. относится к области капиллярных явлений.Характерная величина, определяющая фазовое состояние в-ва, e(Т, р) — отношение ср. потенц. энергии вз-ствия молекул к их ср. кинетич. энергии, зависящее от Т и р. Для Ж. e(Т, р)=1, это означает, что интенсивности упорядочивающих межмол. вз-ствий и разупорядочивающего теплового движения молекул имеют сравнимые значения, чем и определяется вся специфичность жидкого состояния в-ва (для тв. тел e(T, р)->1, для газов e(T, р)-1). Тепловое движение молекул Ж. состоит из сочетания коллективных колебат. движений того же типа, что и в крист. телах, и происходящих время от времени скачков молекул из одних временных положений равновесия (центров колебаний) в другие. Каждый скачок происходит при сообщении молекуле энергии активации, достаточной для разрыва её связей с окружающими молекулами и перехода в окружение др. молекул. В результате большого числа таких скачков молекулы Ж. более или менее быстро перемешиваются (происходит самодиффузия, к-рую можно наблюдать, напр., методом меченых атомов). Характерные частоты скачков составляют 1011 — 1012 с-1 для низкомол. Ж., много меньше — для высокомолекулярных, а в отд. случаях, напр. для сильновязких Ж. и стёкол, могут оказаться чрезвычайно низкими.Колебат. часть теплового движения ч-ц Ж. может быть описана с помощью набора дебаевских волн, к-рые могут проявляться в спектрах Мандельштама — Бриллюэна рассеяния и рассеяния нейтронов. Неупорядоченная часть движения молекул, связанная гл. обр. с тепловым трансляц. движением, проявляется в спектрах рассеянных жидкостью пучков света или нейтронов в виде дополнительной несмещённой довольно интенсивной компоненты, отсутствующей у кристаллов. Термодинамич. теория рассеяния света объясняет её как результат рассеяния света на флуктуациях энтропии. Изучение спектров рассеянных света и нейтронов явл. мощным инструментом исследования поляризационных и др. коллективных движений в Ж.При наличии внеш. силы, сохраняющей своё направление более длит. время, чем интервалы между скачками, молекулы перемещаются в ср. в направлении этой силы. Т. о., статич. или НЧ механич. воздействия приводят к проявлению текучести Ж. как суммарному эффекту от большого числа мол. переходов между временными положениями равновесия. При частоте воздействий, превышающей характерные частоты мол. скачков, у Ж. наблюдаются упругие эффекты (напр., сдвиговая упругость), типичные для тв. тел.В рамках мол. теории однородность и изотропность нормальных Ж. объясняется отсутствием у них дальнего порядка во взаимных положениях и ориентациях молекул (см. ДАЛЬНИЙ И БЛИЖНИЙ ПОРЯДОК). Положения и ориентации двух или более молекул, расположенных далеко друг от друга, оказываются статистически независимыми. В жидких кристаллах дальний порядок наблюдается лишь в ориентации молекул, но отсутствует в расположении их центров масс.Ж. иногда разделяют на неассоциированные и ассоциированные, в соответствии с простотой или сложностью их термодинамич. св-в. Предполагается, что в ассоциированных Ж. есть сравнительно устойчивые группы молекул — комплексы, проявляющие себя как одно целое. Существование подобных комплексов в нек-рых р-рах доказывается прямыми физ. методами. Наличие устойчивых ассоциаций молекул в однокомпонентных Ж. недостоверно.Основой совр. мол. теорий жидкого состояния послужило эксперим. обнаружение методами рентгеновского структурного анализа и нейтронографии ближнего порядка в Ж.— согласования (корреляции) во взаимных положениях и ориентациях близко расположенных групп, состоящих из двух, трёх и большего числа молекул. Эти статистич. корреляции, определяющие мол. структуру жидкости, простираются на область протяжённостью порядка неск. межат. расстояний и исчезают для далеко расположенных друг от друга ч-ц (отсутствие дальнего порядка).По структуре и способам описания Ж. делят на простые и сложные. К первому классу относят однокомпонентные атомарные жидкости (жидкие чистые металлы, сжиженные инертные газы и, с нек-рыми оговорками, Ж. с малоат. симметричными молекулами, напр. ССl4). Для описания их св-в достаточно указать взаимное расположение атомов. Для простых Ж. результаты рентгеноструктурного или нейтронографич. анализа могут быть выражены с помощью т. н. радиальной функции распределения g(r) (рис.). Эта ф-ция характеризует распределение ч-ц вблизи произвольно выбранной ч-цы, т. к. значения g(r) пропорц. вероятности нахождения двух ч-ц на нек-ром заданном расстоянии r друг от друга.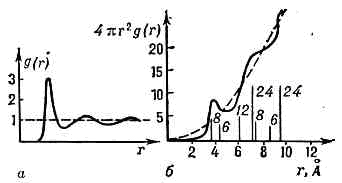 Вид радиальной ф-ции распределения g(r) для жидкого натрия (в условных ед.): а — распределение ч-ц в зависимости от расстояния r; б — число ч-ц в тонком сферич. слое как ф-ции расстояния r (вертикальные отрезки — положения атомов в крист. натрии, числа при них — кол-во атомов в соответствующих координац. сферах, т. н. координац. числа). Пунктиром показано распределение атомов при отсутствии упорядоченности в их расположении (газ).Ход кривой g(r) свидетельствует о существовании определ. упорядоченности в простой Ж.— в ближайшее окружение каждой ч-цы входит в среднем определ. число ч-ц. Для каждой Ж. детали ф-ции g(r) незначительно меняются с изменением Т и р. Расстояние до первого пика определяет ср. межат. расстояние, а по площади под первым пиком можно установить ср. число «соседей» атома в Ж. (ср. координационное число). В большинстве случаев эти хар-ки вблизи линии плавления оказываются близкими к тем же величинам в соответствующем кристалле, однако, в отличие от кристалла, они явл. не постоянными числами, а изменяющимися во времени, и по графику устанавливаются лишь их ср. значения. При сильном нагревании Ж. и приближении её к газовому состоянию ход ф-ции g (r) сглаживается соотв. уменьшению степени ближнего порядка. В разреженном газе g(r)»1. Для сложных Ж. и для жидких смесей расшифровка результатов структурных исследований более трудна и во мн. случаях полностью не может быть осуществлена. Исключение составляют вода и нек-рые другие низкомол. Ж., для к-рых имеются довольно полные исследования и описания их статистич. структуры. Ф-ция g(r) может быть определена методом функций Грина или с помощью разл. приближённых интегр. ур-ний.Теория кинетич. и динамич. св-в Ж. (диффузии, вязкости, динамики флуктуации и т. д.) разработана менее полно, чем теория равновесных св-в (ур-ния состояния, теплоёмкости и др.).В теории Ж. большое развитие получили числ. методы, позволяющие рассчитывать св-ва простых Ж. с помощью быстродействующих ЭВМ — методы Монте-Карло и мол. динамики. Наибольший интерес представляет метод мол. динамики, непосредственно моделирующий на ЭВМ совместное тепловое движение большого числа молекул (при заданном законе их вз-ствия) и по прослеженным траекториям многих отд. ч-п восстанавливающий все необходимые статистич. сведения о системе. Таким путём получены точные теор. результаты относительно структуры и термодинамич. св-в многих простых Ж.Отд. проблему составляет вопрос о структуре и св-вах простых Ж. в непосредств. окрестности критич. точки. Большие успехи здесь достигнуты методами теории подобия (гипотеза масштабной инвариантности).Отд. проблему составляет вопрос о структуре и св-вах жидких металлов, на к-рые значит. влияние оказывают имеющиеся в них коллективизиров. эл-ны. Несмотря на нек-рые успехи, полной электронной теории жидких металлов ещё не существует. Значительные (пока ещё не преодоленные) трудности встретились при объяснении св-в жидких ПП.Основные методы исследований жидкости. Многочисленные макроскопич. св-ва Ж. изучаются методами механики, физики и физ. химии. Равновесные механич. и тепловые св-ва Ж. (сжимаемость, теплоёмкость и др.) изучаются термодинамич. методами. Важнейшей задачей явл. нахождение уравнения состояния для давления и энергии как ф-ции от плотности и темп-ры, а в случае р-ров — и от концентраций компонентов. Знание ур-ния состояния позволяет методами термодинамики установить многочисл. связи между разл. механич. и тепловыми хар-ками Ж. Имеется большое число эмпирич., полуэмпирич. и приближённых теор. ур-ний состояния для разл. индивидуальных жидкостей и их групп.Неравновесные тепловые и механич. процессы в Ж. (напр., диффузия, теплопроводность, электропроводность), особенно в смесях и при наличии хим. реакций, изучаются методами термодинамики необратимых процессов.Механич. движения Ж. как сплошной среды изучаются в гидродинамике. Важнейшее значение имеет Навье — Стокса уравнение, описывающее движение вязкой Ж. У т. н. ньютоновских Ж. (вода, низкомолекулярные органич. Ж., расплавы солей и др.) вязкость не зависит от режима течения (в условиях ламинарного течения, когда Рейнольдса число R
Вид радиальной ф-ции распределения g(r) для жидкого натрия (в условных ед.): а — распределение ч-ц в зависимости от расстояния r; б — число ч-ц в тонком сферич. слое как ф-ции расстояния r (вертикальные отрезки — положения атомов в крист. натрии, числа при них — кол-во атомов в соответствующих координац. сферах, т. н. координац. числа). Пунктиром показано распределение атомов при отсутствии упорядоченности в их расположении (газ).Ход кривой g(r) свидетельствует о существовании определ. упорядоченности в простой Ж.— в ближайшее окружение каждой ч-цы входит в среднем определ. число ч-ц. Для каждой Ж. детали ф-ции g(r) незначительно меняются с изменением Т и р. Расстояние до первого пика определяет ср. межат. расстояние, а по площади под первым пиком можно установить ср. число «соседей» атома в Ж. (ср. координационное число). В большинстве случаев эти хар-ки вблизи линии плавления оказываются близкими к тем же величинам в соответствующем кристалле, однако, в отличие от кристалла, они явл. не постоянными числами, а изменяющимися во времени, и по графику устанавливаются лишь их ср. значения. При сильном нагревании Ж. и приближении её к газовому состоянию ход ф-ции g (r) сглаживается соотв. уменьшению степени ближнего порядка. В разреженном газе g(r)»1. Для сложных Ж. и для жидких смесей расшифровка результатов структурных исследований более трудна и во мн. случаях полностью не может быть осуществлена. Исключение составляют вода и нек-рые другие низкомол. Ж., для к-рых имеются довольно полные исследования и описания их статистич. структуры. Ф-ция g(r) может быть определена методом функций Грина или с помощью разл. приближённых интегр. ур-ний.Теория кинетич. и динамич. св-в Ж. (диффузии, вязкости, динамики флуктуации и т. д.) разработана менее полно, чем теория равновесных св-в (ур-ния состояния, теплоёмкости и др.).В теории Ж. большое развитие получили числ. методы, позволяющие рассчитывать св-ва простых Ж. с помощью быстродействующих ЭВМ — методы Монте-Карло и мол. динамики. Наибольший интерес представляет метод мол. динамики, непосредственно моделирующий на ЭВМ совместное тепловое движение большого числа молекул (при заданном законе их вз-ствия) и по прослеженным траекториям многих отд. ч-п восстанавливающий все необходимые статистич. сведения о системе. Таким путём получены точные теор. результаты относительно структуры и термодинамич. св-в многих простых Ж.Отд. проблему составляет вопрос о структуре и св-вах простых Ж. в непосредств. окрестности критич. точки. Большие успехи здесь достигнуты методами теории подобия (гипотеза масштабной инвариантности).Отд. проблему составляет вопрос о структуре и св-вах жидких металлов, на к-рые значит. влияние оказывают имеющиеся в них коллективизиров. эл-ны. Несмотря на нек-рые успехи, полной электронной теории жидких металлов ещё не существует. Значительные (пока ещё не преодоленные) трудности встретились при объяснении св-в жидких ПП.Основные методы исследований жидкости. Многочисленные макроскопич. св-ва Ж. изучаются методами механики, физики и физ. химии. Равновесные механич. и тепловые св-ва Ж. (сжимаемость, теплоёмкость и др.) изучаются термодинамич. методами. Важнейшей задачей явл. нахождение уравнения состояния для давления и энергии как ф-ции от плотности и темп-ры, а в случае р-ров — и от концентраций компонентов. Знание ур-ния состояния позволяет методами термодинамики установить многочисл. связи между разл. механич. и тепловыми хар-ками Ж. Имеется большое число эмпирич., полуэмпирич. и приближённых теор. ур-ний состояния для разл. индивидуальных жидкостей и их групп.Неравновесные тепловые и механич. процессы в Ж. (напр., диффузия, теплопроводность, электропроводность), особенно в смесях и при наличии хим. реакций, изучаются методами термодинамики необратимых процессов.Механич. движения Ж. как сплошной среды изучаются в гидродинамике. Важнейшее значение имеет Навье — Стокса уравнение, описывающее движение вязкой Ж. У т. н. ньютоновских Ж. (вода, низкомолекулярные органич. Ж., расплавы солей и др.) вязкость не зависит от режима течения (в условиях ламинарного течения, когда Рейнольдса число Rполимеры, стёкла в интервале размягчения, эмульсии и др.}. Св-ва неньютоновских Ж. изучает реология. Специфич. особенности течения жидких металлов, связанные с их электропроводностью и подверженностью влиянию магнитных полей, изучаются в магнитной гидродинамике. Приложения методов гидродинамики к задачам мол. физики жидкостей изучаются в физ.-хим. гидродинамике.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ЖИДКОСТЬ
-
- вещество в конденсир. состоянии, промежуточном между твёрдым и газообразным. Область существования Ж. ограничена со стороны низких темп-р фазовым переходом в твёрдое состояние (кристаллизацией),а со стороны высоких темп-р - в газообразное (испарение). Для каждого вещества характерна критич. темп-pa (при определённом давлении), выше к-рой Ж. не может сосуществовать со своим насыщенным паром. Как правило, вещества имеют одну жидкую модификацию, исключение составляют квантовые Ж. 3 Не и 4 Не, к-рые могут находиться в нормальной и сверхтекучей фазах, а также жидкие кристаллы, у к-рых существуют как нормальная (изотропная) фаза, так и анизотропные фазы. Структура и физ. свойства Ж. зависят от хим. индивидуальности образующих её частиц и от характера и величины сил взаимодействия между ними. Можно выделить неск. групп Ж. (в порядке возрастания сложности). 1) Атомарные Ж. или Ж. из атомов или сферич. молекул (Аr, СH4), связанных центральными ван-дер-ваальсовыми силами. 2) Ж. из двухатомных молекул, содержащих одинаковые атомы (Н 2, N2); в отличие от Ж. первой группы, обладают электрич. квадрупольным моментом. 3) Жидкие непереходные металлы (Na, Hg), в к-рых частицы (ионы) связаны дальнодействующими кулоновскими силами. 4) Ж., состоящие из полярных молекул (НВr), связанных диполь-дипольным взаимодействием. 5) Ассоциированные Ж., пли Ж. с водородными связями (вода, глицерин). 6) Ж., состоящие из больших молекул, для к-рых существенны внутр. степени свободы. Ж. первых двух групп обычно наз. простыми; к ним часто относят и жидкие металлы. Простые Ж. изучены лучше других, из непростых Ж. наиб. хорошо изучена вода. Структура и молекулярное объяснение свойств Ж. из многоатомных молекул со сложными взаимодействиями изучены много хуже. Состояние системы (твердое, жидкое, газообразное) определяется физ. условиями, в к-рых она находится, гл. обр. темп-рой Т и давлением р. Характерным параметром системы является e=e(T, р) - отношение ср. энергии взаимодействия молекул (в расчёте на одну молекулу) к её ср. кинетич. энергии. Для большинства твёрдых тел (при темп-pax, достаточно далёких от темп-ры плавления) e>1; это означает, что в твёрдых телах силы сцепления между молекулами, несмотря на тепловое движение, удерживают их вблизи равновесных положений. В газах e<1 - силы притяжения недостаточны, чтобы удерживать молекулы друг возле друга, вследствие чего частицы газа хаотично движутся с разл. скоростями. В Ж. e@1, что и определяет её особенности и промежуточный характер теплового движения частиц. Структуру жидкостей изучают с помощью методов рентгеновского структурного анализа, электронографии и нейтронографии. Эксперим. исследования показали, что Ж. обладают определённой структурой. Ближайшие соседи каждой молекулы Ж. в среднем располагаются в к.-л. порядке, так что число ближайших соседей и их взаимное расположение в среднем для всех молекул одинаково, это означает, что в Ж. существует ближний порядок. Число частиц dN в сферич. слое толщины dr на расстоянии r от произвольно выбранной частицы равно:
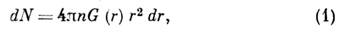
где G(r) - радиальная ф-ция распределения (РФР), п - плотность частиц (ср. число частиц в единице объёма). Для Ж. при темп-pax, не слишком далёких от томп-р плавления, ф-ция G(r )имеет неск. максимумов (обычно не больше трёх), положения к-рых соответствуют ср. расстояниям от данной выбранной молекулы до первых, вторых и т. д. соседей (рис. 1).В кристалле вероятность нахождения атома вне узлов кристаллич. структуры близка к нулю, т. е. атомы в нём в среднем находятся в фиксир. положениях; в Ж. атом с большей или меньшей вероятностью может находиться на разных расстояниях от др. атомов. Вблизи начала координат G(r)@0, а r порядка эфф. диаметра частицы, что свидетельствует о взаимонепроницаемостичастиц. Расстояния r, соответствующие областям максимумов ф-ции G(r), являются наиб. вероятными расстояниями между частицами, ненулевые значения минимумов свидетельствуют о миграции частиц между разл. координац. сферами.
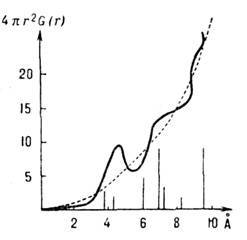
Рис. 1. Вид радиальной функции распределения для жидкого Na (в условных единицах). Пунктир - функция 4pr2G(r), определяющая расположение молекул при отсутствии корреляций (газ). Вертикальные отрезки - положения атомов в кристаллическом Na, числами отмечены координационные числа.
На больших расстояниях G (r)@1,что отражает равновероятность расположения далёких частиц. С повышением темп-ры радиус первой координац. сферы растёт, а число ближайших соседей уменьшается, с понижением темп-ры и увеличением плотности максимумы на кривой G(r )становятся всё более отчётливыми, т. е. степень ближнего порядка увеличивается (рис. 2, 3).
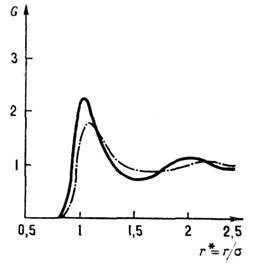
Рис. 2. Влияние плотности на радиальную функцию распределения для системы, взаимодействия частиц в которой описываются потенциалом Леннард-Джонса. Сплошная кривая:Т*= kT/e = 2,89; n*=ns3=0,85(e, s - параметры потенциала). Пунктирная кривая: T*=2,64; n* = 0,55. Кривые построены по результатам молекулярно-динамических расчётов.
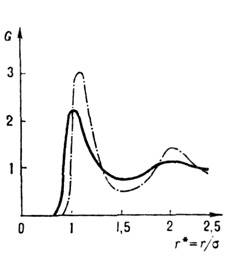
Рис. 3. Влияние температуры на радиальную функцию распределения системы, взаимодействия частиц в которой описываются потенциалом Леннард-Джонса. Сплошная кривая: T* = 2,89; n*=0.85. Пунктирная кривая: Т* = 0,68; n* = 0,85. Кривые построены по результатам молекулярно-динамических расчётов.
Для Т, близких к темп-ре плавления, координац. числа Zi близки к их значениям в соответствующем твёрдом теле (напр., для жидкого Аr, имеющего Т пл=83,4 К, при Т=84,4 К Z1=10,2-10,9, a Z2=5; для твёрдого Аr, имеющего гранецентрир. решётку, Z1=12, a Z2=6). Кроме того, положения максимумов на кривой G(r )очень близки к расстояниям до первых, вторых и т. д. соседей в кристаллич. решётке. Числа Zi в Ж., в отличие от координац. чисел в кристалле, являются лишь ср. характеристиками структуры. Истинные (мгновенные) значения Zi испытывают очень сильные тепловые флуктуации, достигающие даже вблизи темп-ры плавления ~20%. При повышении темп-ры эти флуктуации ещё более возрастают и ср. значения Zi уже не могут служить характеристиками структуры Ж. Вблизи темп-ры плавления различие плотностей и сил сцепления в жидком и твёрдом состояниях невелики и характер теплового движения частиц в Ж. сохраняет нек-рые черты движений частиц в кристалле. Вдали от критич. точки движение частиц представляет собойнерегулярные колебания со ср. частотой 1/t0, близкой к частотам колебаний частиц в кристаллах, и амплитудой, определяемой размерами "свободного объёма", предоставленного данной частице её соседями. Центр колебаний определяется флуктуирующим полем соседних частиц и смещается вместе с ними, поэтому, в отличие от кристалла, положения равновесия в Ж. временны, неустойчивы: частицы в Ж. перемещаются путём более или менее редких скачков с преодолением потенц. барьера, разделяющего два возможных положения частицы. В случае несферич. молекул кроме колебаний и скачков должны учитываться вращения частиц и вращат. колебания вокруг связи (для жёстких молекул) и внутр. движения молекул с внутр. степенями свободы. В том случае, когда тепловая энергия молекул становится сравнимой с энергией активации, необходимой для изменения ориентации молекул, вращат. движение может приобретать характер свободного вращения. Различие между вращат. и поступат. движениями в Ж. состоит в том, что при скачкообразных изменениях равновесной ориентации молекулы (если они достаточно малы) могут поворачиваться на большие углы, тогда как при изменениях равновесных положений центр тяжести молекул всегда перемещается на малые расстояния (~10-8 см). Для больших молекул и комплексов применимы представления о диффузионном характере вращат. движений, при к-ром вращения состоят из множества случайных поворотов на очень малые углы около нек-рого направления в пространстве, к-рое само медленно меняется. Время t свободной жизни молекулы во временном положении равновесия между двумя активир. скачками связано с t0 соотношением:
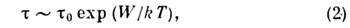
где W - энергия активации. Ср. период колебаний молекул t0~10-12 с, время t>t0 и зависит от природы Ж. и от отношения W/kT. Для Ж. с низкой вязкостью t0~10-11 с и растёт с ростом вязкости, достигая часов и даже суток (у стёкол). Свойства жидкостей. Непрерывно и в большом числе совершающиеся переходы из одного положения равновесия в другое обеспечивают сильно выраженную самодиффузию частиц Ж., а также осн. её свойство - текучесть. Под действием постоянной внеш. силы проявляется преим. направленность скачков частиц Ж. вдоль действия силы, т. е. возникает поток частиц в этом направлении. Если величина приложенной силы мала, то частота скачков 1/t не изменяется. Существенно статистич. механизм этого процесса приводит к пропорциональности потока приложенной силе и, следовательно, конечности величины вязкости (обратной величине текучести).Под действием переменной силы с периодом, намного меньшим t, поведение Ж. резко меняется: механизм текучести не успевает проявиться и проявятся упругие её свойства. При этом возникают не только деформации типа сжатие - растяжение, но и сдвиговые упругие деформации. Действие значит. по величине сил в течение очень короткого промежутка времени может привести к нарушению прочности Ж.: появлению трещин, разломов и т. д. Подобные явления в Ж., связанные с её упругостью и прочностью, экспериментально наблюдаются и сравнительно хорошо изучены. В том случае, когда характерные времена движения Ж. много больше t, она течёт. Обычно упругие деформации в Ж. происходят адиабатически, т. к. теплопроводность их мала (исключение составляют жидкие металлы). Ж. могут выдерживать очень большие растягивающие усилия (порядка сотен атмосфер), не испытывая разрыва, если эти усилия сводятся к всестороннему отрицат. давлению, исключающему возможность течения (напр., при охлаждении сосуда, полностью заполненного жидкостью, если коэф. расширения Ж. больше коэф. расширения вещества сосуда).Механич. свойства Ж. описываются набором сохранения законов (числа частиц, импульса и энергии). Записанные в локальной форме эти законы представляют собой систему ур-ний в частных производных - ур-ний гидродинамики. Феноменологич. описание термодинамич. свойств содержится в ур-нии состояния p=f(n, Т), причём наряду со строгими ур-ниями состояния (см. ниже) существует большое число полуэмпирич. ур-ний (наиб. простое из к-рых - Ван-дер-Ваалъса уравнение). Ур-ние состояния позволяет вычислить термодинамич. характеристики Ж.: теплоёмкость, сжимаемость и т. д. Статистическая теория жидкостей. Равновесные свойства Ж. полностью описываются набором ф-ций распределения FS(r1, ..., rS), описывающих плотность вероятности нахождения частиц в точках r1 ..., rS.[В частном случае s=2, F2(r1, r2)=G(r1-r2).] Физ. свойства Ж. (давление р, плотность энергии E, сжимаемость) в случае парного и центрального взаимодействия между частицами выражаются только через G(r): давление
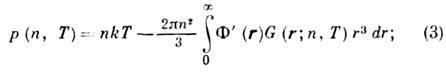
плотность энергии

сжимаемость
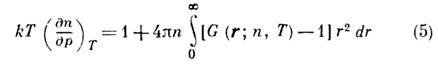
[Ф(r) - потенциал парного взаимодействия]. При наличии в Ж. многочастичного взаимодействия термодинамич. характеристики кроме G(r )будут содержать старшие ф-ции распределения. Формализм ф-ций распределения развит Н. Н. Боголюбовым, М. Борном (М. Born), Дж. Грином (G. Green) и Дж. Г. Кирквудом (J. G. Kirkwood). Парное взаимодействие характерно для гелия жидкого. В жидких металлах непрямое взаимодействие ионов приводит к многочастичным силам, зависящим от плотности. Ф-ции FS удовлетворяют системе ур-ний Боголюбова - Берна - Грина - Кирквуда - Ивона (ББГКИ; см. Боголюбова уравнение). Сложность решения этой системы интегро-дифференциальных ур-ний состоит в том, что в ур-ние для FS входит ф-ция FS+1, т. e. уравнения являются зацепляющимися. Они не имеют точных решений и решаются с помощью разл. приближённых методов. Для газа решение находится разложением в степенной ряд по плотности. Интегрирование этих рядов с использованием (3), (4) и (5) даёт соответствующие вириальные разложения. Для плотных Ж. применяют суперпозиц. приближение, в к-ром нек-рая ф-ция FS представляется в виде произведения или суммы произведений ф-ций с меньшими номерами. При этом система ур-ний ББГКИ становится конечной. Наиб. распространено приближение Кирквуда
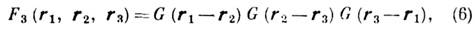
к-рое приводит к замкнутому ур-нию для G(r); решения этого ур-ния для разл. плотностей и темп-р хорошо изучены и качественно правильно описывают поведение G(r). Однако результаты, полученные молекулярной динамики методом и Монте-Карло методом, свидетельствуют о неудовлетворительности суперпозиц. приближения. Наиб. успешно структура и термодинамич. свойства Ж. описываются с помощью Перкуса - Йевика уравнения (ПЙ); если воспользоваться Орнштейна- Цернике уравнением
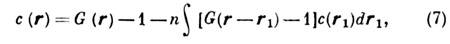
связывающим прямую корреляц. ф-цию с (r) и G(r), то ур-ние ПЙ получается при допущении
c(r) = G(r){1 - ехр[Ф(r)/kТ]}.(8)
Ур-ние ПЙ имеет аналитич. решение для системы твёрдых шаров, к-рое удовлетворительно описывает структуру Ж. при определённом выборе диаметра шаров (рис. 4).
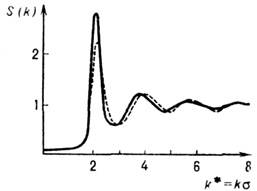
Рис. 4. Структурный фактор
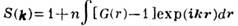 жидкого Nа при 373К. Сплошная кривая получена экспериментально, пунктирная - по уравнению Перкуса - Йевика (h = 0,45).
жидкого Nа при 373К. Сплошная кривая получена экспериментально, пунктирная - по уравнению Перкуса - Йевика (h = 0,45).Ур-ние состояния Ж. из твёрдых шаров, полученное из аналитич. решения ур-ния ПЙ с помощью ур-ния (5), имеет вид:

где h=(1/6)pnd3 - безразмерная плотность, d - диаметр шаров. На рис. 5 результаты, полученные с помощью ур-ний состояния для системы твёрдых шаров, сравниваются с точными результатами, полученными методом молекулярной динамики.
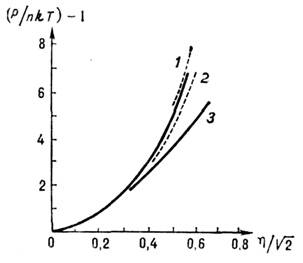
Рис. 5. Уравнение состояния системы твёрдых сфер. Сплошная кривая получена методом молекулярной динамики; кривая 1 - с помощью уравнения Перкуса-Йевика и уравнения (5); 2 - спомощью уравнения Перкуса-Йевика и уравнения (3); 3 - спомощью суперпозиционного приближения (6).
Наиболее успешно описание структуры и свойств жидкости достигается в теории возмущений, в к-рой модель твёрдых шаров принимается в качестве нулевого приближения, а силы притяжения считаются возмущением. Полученные таким путём термодинамич. характеристики хорошо согласуются с экспериментальными данными. Статистич. теория кинетич. процессов в Ж. основана на исследовании неравновесных ф-ций распределения FS( х1, . . ., xS, t )для групп из s=l, 2, ... молекул; xi(ri, pi) - набор координат и импульсов молекул. Если в системе действуют только парные центр. силы, то ф-ции FS удовлетворяют системе зацепляющихся интегро-дифференциальных ур-ний ( Боголюбова уравнений):
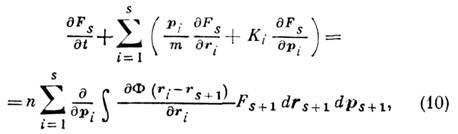
где Ki - сила, действующая на i -ю частицу со стороны остальных выбранных s-1 частиц и внеш. полей. Для построения теории кинетич. процессов в Ж., упростив задачу, можно ограничиться вместо бесконечной цепочки ур-ний (10) только двумя ур-ниями для ф-ций F1 и F2. Ур-ния (10) обратимы во времени, и, чтобы получитьрешения, описывающие необратимые кинетич. процессы, обычно переходят к новым ф-циям
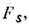 являющимсярезультатом усреднения или "размазывания" ф-ций FS по соответствующим образом подобранным малым интервалам времён; ур-ния для
являющимсярезультатом усреднения или "размазывания" ф-ций FS по соответствующим образом подобранным малым интервалам времён; ур-ния для 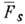 наз. кинетическими. Такие ур-ния получаются, в частности, если пренебречь изменениями ф-ций FS в течение времени порядка времени столкновения частиц (на т. н. стадии разрушения нач. корреляций). Если плотность мала, то для решения системы (10) можно воспользоваться разложением в ряд по степеням плотности. Первое приближение приводит к ур-нию Больцмана (см. Кинетическое уравнение Больцмана )для F1, из к-рого можно получить выражения для коэф. переноса. Исследование следующих приближений показывает, что вириального разложения для коэф. переноса не существует, т. к. они не являются аналитич. ф-циями плотности. Напр., для коэф. теплопроводности (справедливо разложение:
наз. кинетическими. Такие ур-ния получаются, в частности, если пренебречь изменениями ф-ций FS в течение времени порядка времени столкновения частиц (на т. н. стадии разрушения нач. корреляций). Если плотность мала, то для решения системы (10) можно воспользоваться разложением в ряд по степеням плотности. Первое приближение приводит к ур-нию Больцмана (см. Кинетическое уравнение Больцмана )для F1, из к-рого можно получить выражения для коэф. переноса. Исследование следующих приближений показывает, что вириального разложения для коэф. переноса не существует, т. к. они не являются аналитич. ф-циями плотности. Напр., для коэф. теплопроводности (справедливо разложение:(=(0+а1n+a2n2lnn+а3 п2+. . . ,(11)
где (0 - больцмановское выражение для теплопроводности. Для плотных Ж. осн. проблема состоит в оценке правой части (10), наз. интегралом столкновений. Кирквудом предложены кинетич. ур-ния для ф-ций
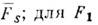 Оно имеет вид:
Оно имеет вид: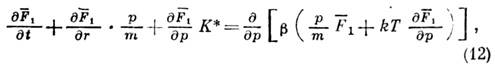
где т - масса молекулы Ж.; сила К* равна сумме внеш. силы и дополнит. члена статистич. природы, связанного с отклонением системы от равновесного состояния (последним слагаемым обычно пренебрегают); b - коэф. трения. Аналогичные ур-ния получаются и для ф-ций
 с большими номерами. Если внеш. силы, градиенты темп-ры, плотности и т. д., ответственные за неравновесность состояния системы, малы, то ур-ния для
с большими номерами. Если внеш. силы, градиенты темп-ры, плотности и т. д., ответственные за неравновесность состояния системы, малы, то ур-ния для 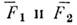 могут быть решены в виде
могут быть решены в виде 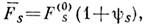 где F(0)S - равновесные ф-циираспределения и yS - малые поправки на неравновесность; при этом координатная часть y2 ф-ции
где F(0)S - равновесные ф-циираспределения и yS - малые поправки на неравновесность; при этом координатная часть y2 ф-ции 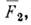 описывающая отклонение радиальной ф-ции распределения частиц от равновесного значения, особенно важна. С помощью ф-ций
описывающая отклонение радиальной ф-ции распределения частиц от равновесного значения, особенно важна. С помощью ф-ций 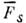 можпо получить для сдвиговой h и объёмной x вязкости выражения:
можпо получить для сдвиговой h и объёмной x вязкости выражения: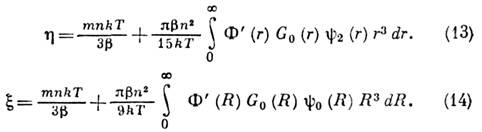
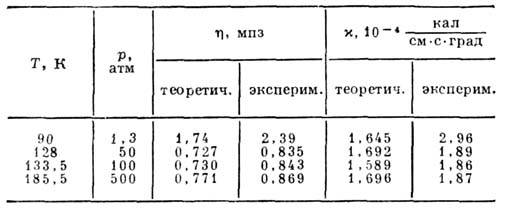
Первые слагаемые в правых частях ур-ний (13) и (14) связаны с переносом импульса при движении молекул, и для Ж. ими можно пренебречь по сравнению со вторыми слагаемыми, связанными с переносом импульса взаимодействием молекул. Рассмотренная статистич. теория (теория Кирквуда) учитывает только одну составляющую теплового движения молекул - броуновское движение во флуктуирующем поле и не учитывает столкновений. Обобщение ур-ния Кирквуда с учётом столкновений, в к-рых молекула ведёт себя как твёрдая сфера, приводит к тому, что в выражениях типа (13), (14) появляются дополнит. члены, обусловленные столкновениями (теория Райса- Олнетта). В табл. приведены полученные экспериментально и рассчитанные с помощью таких ур-ний значения h и ( для жидкого аргона:
Др. способ вычисления коэф. переноса в Ж. связан с нахождением временных корреляц. ф-ций (ВКФ). Идея метода основана на гипотезе Онсагера: эволюция неравновесного состояния системы не зависит от того, оказалась она в этом состоянии под действием внеш. возмущения или в результате флуктуации (по крайней мере для малых возмущений). Это позволяет найти связь между коэф. переноса, характеризующими необратимую эволюцию системы в направлении к равновесному состоянию, и ВКФ. При этом коэф. переноса выражаются через интегралы от ВКФ соответствующих потоков (см. Кубо формулы). Напр., коэф. сдвиговой вязкости равен:
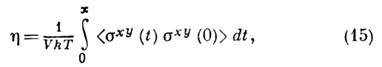
где sxy(t) - микроскопический (в фазовом пространстве) тензор потока импульса, или тензор напряжений. Объёмная вязкость выражается аналогичным образом через диагональные компоненты тензора sik. Коэф. теплопроводности определяется автокорреляц. ф-цией векторов теплового потока. Прямые вычисления по ф-лам типа (15) выполнить сложно, т. к. для нахождения зависимости sik(t )и последующего усреднения необходимо решить задачу N тел. Расчёты ВКФ, выполненные методами молекулярной динамики, привели к обнаружению медленного затухания ВКФ со временем, имеющего степенной, а не экспоненциальный (как, напр., в теории броуновского движения) характер. Для упомянутых коэф. переноса ВКФ затухают по закону t -d/2, где d- размерность пространства. Можно показать аналитически (напр., в случае коэф. самодиффузии), что физ. причина неэкспоненциального "хвоста" корреляц. ф-ции обусловлена тем, что на больших временах эволюция возмущений в Ж. происходит по законам макроскопич. гидродинамики, характерные времена к-рых намного больше быстрых экспоненциальных переходных процессов. Помимо медленного затухания ВКФ эксперименты по молекулярной динамике обнаружили выход ВКФ скорости молекулы в отрицат. область, что ещё раз подтверждает наличие колебат. моды движения молекул в Ж. Лит.: Дебай П., Квазикристаллическая структура жидкостей, пер. с нем., "УФН", 1939, т. 21, с. 120; К i r k w о о d J. G., The statistical mechanical theory of transport processes, 1. General theory, "J. Chem. Phys.", 1946, v. 14, p. 180; Born M., Green H. S., A general kinetic theory of liquids, Camb., 1949; Корнфельд М., Упругость и прочность жидкостей, М.-Л., 1951; Фишер И. 3., Статистическая теория жидкостей, М., 1961; его же, Гидродинамическая асимптотика автокорреляционной функции скорости молекулы в классической жидкости, "ЖЭТФ", 1971, т. 61, с. 1647; Боголюбов Н. Н., Проблемы динамической теории в статистической физике, Избр. труды, т. 2, К., 1970; Физика простых жидкостей, под ред. Г. Темперли, пер. с англ., М., 1971; Weeks J. D., Chandler D., Andersen Н. С., Role of repulsive forces in determining the equilibrium structure of simple liquids, "J. Chem. Phys.", 1971, v. 54, p. 5237; Коваленко Н. П., Фишер И. 3., Метод интегральных уравнений в статистической теории жидкостей, "УФН", 1972, т. 108, с. 209; Бровман Е. Г., Каган Ю. М., Фононы в непереходных металлах, "УФН", 1974, т. 112, с. 369; Френкель Я. И., Кинетическая теория жидкостей, Л., 1975; Б а л е с к у Р., Равновесная и неравновесная статистическая механика, пер. с англ., т. 1-2, М., 1978; Крокстон К., Физика жидкого состояния, пер. с англ., М., 1978; Форстер Д., Гидродинамические флуктуации, нарушенная симметрия и корреляционные функции, пер. с англ., М., 1980;Динамические свойства твёрдых тел и жидкостей, пер. с англ., М., 1980; К о v а 1 е n k о N. Р., К u z m i n a L. M., The influence of many-body interaction of the speed of sound in liquid metals, "Phys. Stat. Sol. (b)", 1984, v. 124, p. 537. Н. П. Коваленко, И. З. Фишер.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.