Akademik

RADIOACTIVITÉ

On appelle radioactivité la transformation spontanée d’un noyau atomique au cours de laquelle ce dernier émet un rayonnement. L’observation des effets de ce rayonnement a conduit à la découverte de la radioactivité et des radio-éléments. On classe ainsi les éléments présents dans la nature en deux catégories: ceux dont les noyaux ne subissent au cours du temps aucune transformation et ceux dont les noyaux émettent un rayonnement à un moment de leur existence; les premiers sont dits éléments stables et les seconds éléments radioactifs ou radioéléments ^{[cf. RADIOÉLÉMENTS ET RAYONNEMENTS IONISANTS]}. Parmi les quatre-vingt-douze éléments naturels dénombrés, une douzaine sont radioactifs (on les appelle quelquefois radioéléments naturels). Certains ont tous leurs isotopes radioactifs, par exemple le technétium (Z = 43) et le prométhéum (Z = 61). D’autres n’en ont qu’un seul: c’est le cas du potassium (Z = 19), dont seul l’isotope de nombre de masse A = 40 se transforme spontanément, les isotopes A = 39 et A = 41 étant stables. En fait, depuis 1934, on sait fabriquer des isotopes radioactifs de chaque élément (appelés fréquemment radioéléments artificiels).

Il existe six modes de transformation spontanée (si l’on tient compte de l’émission 塚) auxquels on peut ajouter la radioactivité par émission de protons observée plus récemment. Ces six modes sont:

– L’émission 見, transformation par laquelle un noyau émet une particule 見, c’est-à-dire un noyau d’atome d’hélium ⁴²He constitué de deux protons et de deux neutrons (ex.: ⁸⁸²²⁶Ra⁸⁶²²²Rn + ²⁴He). Par émission 見, l’élément Z se transforme en élément Z 漣 2. Le nombre de nucléons passe de A à A 漣 4. L’émission 見 s’observe pour les éléments lourds (Z 礪 82), mais on l’a aussi mise en évidence pour ⁶²¹⁴⁷Sm et quelques isotopes produits artificiellement dans cette même région du tableau de Mendeleïev.

– L’émission 廓^-, 廓⁺ et la capture électronique. Ces trois modes de transformation sont caractérisés par le fait que le numéro atomique Z du noyau radioactif change d’une unité sans variation du nombre de masse A. Dans l’émission 廓^- (ex.: ¹⁵³²P size=1^廓-1632S), la transformation s’accompagne de l’émission d’un électron négatif appelé 廓^- en général aisément détectable et d’un antineutrino 益 dont la détection est très difficile; le numéro atomique Z de l’élément initial devient Z + 1 pour l’élément final. Dans l’émission 廓⁺, c’est un électron positif 廓⁺ et un neutrino 益 qui sont émis, et Z devient Z 漣 1 (ex.: ¹¹²²Na size=1^廓+1022Ne). La capture électronique est un processus par lequel le noyau radioactif se saisit d’un électron de son cortège en émettant un neutrino 益 et par suite Z diminue d’une unité (ex.: ¹⁸³⁷A+e ^- 轢¹⁷³⁷Cl+ 益). L’observation de cette transformation est plus délicate, puisque le rayonnement d’origine nucléaire est très difficile à mettre en évidence; elle peut être décelée par l’examen du rayonnement X de réarrangement du cortège de l’atome final, puisqu’un électron du cortège (en général, un électron K ou L) a été absorbé et qu’il existe une place vacante dans la couche K ou L.

– La fission spontanée. Pour les éléments très lourds (Z 礪 90), les noyaux ont une probabilité mesurable de subir spontanément la fission, phénomène par lequel le noyau (Z, A) se scinde en deux fragments sensiblement égaux (Z, A)2(Z/2, A/2).

– L’émission 塚. Elle correspond dans un noyau à la transition d’un état quantique à un autre avec émission d’un photon.

Dans cet article, on utilisera, comme il est préconisé officiellement, le mot « nuclide » pour désigner une espèce nucléaire déterminée, caractérisée par un nombre Z de protons et par un nombre total A de nucléons.

1. Découvertes et lois générales

Historique

La radioactivité a été découverte en 1896 par H. Becquerel qui effectuait des recherches sur le rayonnement X récemment mis en évidence par W. C. Röntgen. Becquerel, suivant une suggestion de H. Poincaré, cherchait si les corps fluorescents émettaient un rayonnement susceptible d’impressionner la plaque photographique à travers un papier noir. Divers auteurs avaient signalé des résultats positifs avec le sulfure de zinc et le sulfure de calcium: malgré de nombreux travaux, on ne put renouveler ces résultats. Becquerel fit ses expériences avec des sels d’uranium qu’il exposait au soleil pour les rendre fluorescents. Les résultats furent positifs: mais, lorsque, par manque de soleil, il laissa au voisinage d’une plaque photographique un sel d’uranium, il constata que la plaque était tout de même impressionnée. Il admit que l’uranium émet des rayonnements particuliers qu’on appela «rayons uraniques». Les expériences de Becquerel étaient surtout qualitatives. Marie Curie, sur les conseils de Pierre Curie, entreprit des mesures quantitatives en se référant à l’ionisation produite dans l’air par ces rayonnements (Pierre Curie utilisait la piézo-électricité du quartz qu’il venait de découvrir avec son frère Jacques pour mesurer les très faibles courants d’ionisation). Marie Curie put ainsi montrer, en même temps que G. Schmidt en Allemagne, que le thorium émettait aussi des rayonnements. Dès juillet 1898, avec Pierre Curie, elle annonçait la présence d’un nouvel élément, le polonium (Z = 84), puis, en décembre 1898, avec P. Curie et G. Bémont, l’existence du radium (Z = 88). Elle proposa le nom de «radioactivité» pour désigner le phénomène. De très nombreuses expériences furent entreprises pour déterminer les lois de la radioactivité et découvrir de nouveaux éléments. On put caractériser très vite les rayonnements 見, 廓^- et 塚 (notamment, travaux de E. Rutherford en 1899); mais il fallut attendre 1934 pour que Irène et Frédéric Joliot-Curie mettent en évidence la radioactivité artificielle en montrant que certains éléments légers, par exemple l’aluminium, après transmutation par des particules 見, sont radioactifs et émettent des électrons positifs; leurs expériences conduisaient simultanément à la découverte de la radioactivité artificielle et à celle d’un nouveau mode de désintégration: l’émission 廓⁺. Ils produisaient du ¹⁵³⁰P par la réaction:

suivie de:

En 1937, Luis Alvarez caractérise la capture électronique sur le ²³⁴⁸V en observant les rayons K size=1^見 du titane (Z = 22), et ce n’est qu’après 1940 qu’on a pu mettre en évidence la fission spontanée. Un même nuclide peut se désintégrer suivant plusieurs modes. Ainsi, le ²⁹⁶⁴Cu est émetteur 廓⁺, 廓^- et donne soit ²⁸⁶⁴Ni, soit ³⁰⁶⁴Zn; il peut aussi se transformer par capture électronique pour donner ²⁸⁶⁴Ni; ⁸³²¹²Bi est émetteur 見 et 廓^- et se transforme soit en ⁸¹²⁰⁸Tl, soit en ⁸⁴²¹²Po.

Un noyau radioactif, après sa transformation, conduit soit à un noyau stable, soit à un autre noyau radioactif qui se transformera à son tour. La substance produite est souvent appelée «substance fille» et l’élément initial «substance mère». On observe ainsi plusieurs éléments radioactifs successifs qui constituent une famille radioactive. Les années qui suivirent la découverte de la radioactivité permirent de mettre en évidence que les radioéléments naturels étaient pour l’essentiel répartis en trois familles dont le nom correspondait au premier élément de chacune d’elles: ⁹²²³⁸U, ⁹⁰²³²Th et ⁹²²³⁵U ou actino-uranium. La figure 1 en montre des filiations successives.

Le nombre de masse A des isotopes des divers éléments d’une même famille ne varie que par quatre unités chaque fois qu’il y a un nuclide émetteur 見, les transformations 廓 étant isobariques. Ainsi, tous les membres de la famille du thorium dont le premier élément est le ⁹⁰²³²Th (A = 232 est un multiple de 4) ont des nombres de masse multiples de 4, et cette famille est caractérisée quelquefois par cette propriété et dénommée A = 4 n ^{[cf. RADIOCHIMIE]}.

À la suite de la radioactivité artificielle et surtout de la fission, des filiations successives peuvent être observées fréquemment, conduisant aussi à de véritables familles; par exemple:

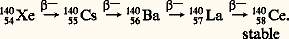
Lois de la radioactivité

La loi de la décroissance radioactive a été explicitée pour la première fois par Rutherford et Soddy en 1902. On peut l’énoncer ainsi: la probabilité pour qu’un atome radioactif se transforme durant un intervalle de temps dt est dt , la quantité, appelée constante radioactive, étant caractéristique du nuclide considéré et pouvant donc servir à l’identifier. ne dépend pas de l’«âge» de l’atome, c’est-à-dire du temps qui le sépare de l’instant de sa formation («les atomes ne vieillissent pas»); caractéristique nucléaire, elle ne dépend pas des combinaisons chimiques ou des conditions physiques de l’élément. (En fait, il ne s’agit là que d’une première approximation, car, d’une part, les interactions noyau-cortège électronique modifient légèrement, dans certains cas, et, d’autre part, les conditions physiques réalisables en laboratoire ne correspondent qu’à un très petit éventail de températures et de pressions.)

Si l’on dispose de N atomes d’un nuclide radioactif à l’instant t , le nombre d N d’atomes qui se désintègrent entre l’instant t et l’instant t + dt est donc:

L’intégration donne N = ⁰ e ^- size=1^凞t , où ⁰ est le nombre d’atomes à l’instant t = 0. La loi de décroissance radioactive est une pure loi statistique. Lorsqu’un nuclide peut se transformer suivant plusieurs modes, la constante est la somme des probabilités des divers modes:

où lesⁱ sont appelées constantes partielles de désintégration.

À partir de, on définit la période et la vie moyenne du nuclide. La période est le temps T au bout duquel, sur un ensemble initial de ⁰ atomes, la moitié de ce nombre est transformée (N⁰ étant très grand devant l’unité); on a donc:

La vie moyenne 精 est la durée de vie moyenne des atomes radioactifs:

Entre période et vie moyenne existe donc la relation:

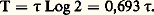
Dans la pratique, c’est la notion de période qui est la plus utilisée. Les périodes varient d’un nuclide à l’autre dans de larges limites, d’une très faible fraction de seconde (10^-6 s ou même 10^-12 s dans le cas de l’émission 塚) à plus de 10¹⁰ ans.

On appelle « activité » d’une substance à l’instant t la quantitéN, où N est le nombre d’atomes présents à cet instant. Pour des substances ayant des poids atomiques peu différents, c’est donc surtout qui détermine cette activité pour un poids de substance donné. D’après d N = 漣N dt , l’activité est le nombre de désintégrations par unité de temps. On a défini l’unité de radioactivité qu’on appelle le becquerel (Bq) qui correspond à une quantité de radioélément donnant une désintégration par seconde. Cette unité remplace le curie (Ci) qui était utilisé jusqu’en février 1982 et qui correspondait à une quantité de radioélément produisant 3,7 練 10¹⁰ désintégrations par seconde (1 curie de radium 226 étant très sensiblement équivalent à 1 gramme); le curie est encore souvent utilisé.

Accumulation des produits en filiation. Équilibre radioactif

Lorsqu’une substance mère A donne naissance à une substance fille B, on a:

Si^A et^B sont les constantes radioactives des nuclides A et B, supposons que, à l’instant initial, on ait A = A⁰ atomes du nuclide A et aucun atome de B, soit B⁰ = 0. À l’instant t , appelons A et B le nombre d’atomes des nuclides A et B; à cet instant, la variation du nombre d’atomes B est donnée par:

où A^A est le nombre d’atomes A qui se transforment en B et où 漣 B^B est le nombre d’atomes B qui disparaissent. L’intégration de cette équation conduit à:

qui fixe l’évolution en fonction du temps du produit B. La quantité B passe par un maximum au temps t ^m lorsqu’on a:

On trouve:

Au temps t ^m , les activités de A et de B sont égales: à cet instant, il y a équilibre radioactif. Si^A 麗^B et si t est suffisamment grand, le rapport des activités de A et de B:

devient constant: c’est l’équilibre de régime (T^A et ^B sont les périodes relatives aux deux substances). Il est possible de généraliser ces considérations à n corps en filiations (équations de Bateman).

2. Émission size=5見

Énergétiquement, un noyau est émetteur 見 par transformation spontanée si sa masse est supérieure à la somme des masses du noyau final et de la particule 見. Pour effectuer ce bilan énergétique, on considère que l’on extrait simultanément deux protons et deux neutrons du noyau qui se condensent en un noyau d’hélium. Lorsque l’énergie de condensation de ces quatre particules est supérieure à l’énergie nécessaire à leur extraction, l’émission 見 est énergétiquement possible. Cette condition est remplie pour un nombre de masse supérieur ou égal à 140. En fait, sauf pour quelques très rares exceptions (par exemple, ⁶²¹⁴⁷Sm, ⁶⁴¹⁵²Gd, ⁷²¹⁷⁴Hf), on n’observe l’émission 見 que pour A 礪 208: ce fait est dû à ce que l’énergie disponible pour A 麗 208 est trop faible et conduit (cf. infra ) à une constante radioactive trop longue pour être observable. Vers A = 208, une discontinuité se produit dans l’énergie des 見; cette brusque augmentation provient de la formation de l’ensemble saturé: quatre-vingt-deux protons et cent vingt-six neutrons ^{[cf. NOYAU ATOMIQUE]}. En toute rigueur, l’énergie disponible E n’est pas strictement l’énergie E size=1^見 emportée par la particule 見; l’émission 見 provoque un recul du noyau (conservation de la quantité de mouvement) et E = E size=1^見 + E^R avec E size=1^見 = EM/(M + m ) et E^R = Em /(M + m ), où M représente la masse du noyau final et m la masse de la particule 見. L’énergie des particules 見 émises se situe pour les divers nuclides entre 5 et 9 MeV approximativement.

Structure fine et longs parcours

Le noyau initial étant supposé dans son état fondamental, si l’émission 見 conduit au noyau final dans son état fondamental, les particules émises doivent toutes avoir la même énergie. L’expérience a confirmé cette manière de voir (c’est le cas du ⁸⁴²¹⁰Po à une très bonne approximation). L’énergie des particules 見 est mesurable avec une précision supérieure au dix-millième à l’aide d’un spectrographe magnétique. Les spectrographes les plus utilisés sont des spectrographes semi-circulaires où les particules de même énergie sont focalisées après avoir parcouru une demi-circonférence, et l’image d’une source apparaît comme une raie sur le plan focal. S. Rosenblum a découvert, en 1929, que certains nuclides, au lieu d’une seule raie, donnaient une série de raies d’énergies voisines. Ce phénomène, appelé «structure fine», s’interprète par le fait que le noyau final peut se trouver dans divers états excités (fig. 2); l’étude de la structure fine est une excellente méthode de détermination directe des états excités. Dans le phénomène de longs parcours, le noyau initial se trouve lui-même dans un état excité et peut se transformer par émission 見 avant d’avoir atteint le niveau fondamental. L’énergie des particules 見 émises est alors plus grande que l’énergie des particules 見 entre états fondamentaux (fig. 3). Ce phénomène est beaucoup plus rare que celui de structure fine, puisque la vie moyenne d’un noyau dans un état excité est en général faible et que la probabilité d’émission de photons est beaucoup plus grande que la probabilité d’émission de particules 見.

Théorie de l’émission size=5見

Un noyau émetteur possède une certaine stabilité (vie moyenne 拾 10^-20 s) en raison de l’existence d’une barrière de potentiel. La figure 4 représente la variation de l’énergie potentielle entre une particule 見 et un noyau de charge Z en fonction de la distance qui les sépare. À grande distance (r 拾 R, rayon du noyau), la particule 見 est soumise au potentiel coulombien répulsif. À la distance R, elle est en contact avec le noyau et l’attraction des forces nucléaires devient plus importante que la répulsion coulombienne. À l’intérieur du noyau, la particule 見 a l’énergie E. La hauteur de la barrière de potentiel (valeur de l’énergie coulombienne répulsive entre le noyau et la particule 見 lorsque cette dernière est à la surface du noyau) est évaluée par l’expression B = 2 Ze ²/4 神﨎⁰R, où Z est le numéro atomique du noyau final. Si l’on suppose que le moment angulaire de la particule 見 par rapport au noyau est nul, B est de l’ordre de 30 MeV pour les noyaux lourds. La mécanique quantique fournit l’explication du fait que la particule 見 possède une certaine probabilité par unité de temps de traverser cette barrière.

Si l’on suppose que la particule 見 est préformée dans le noyau et qu’elle a une vitesse v 見, le temps moyen qui sépare deux impacts successifs est de l’ordre de 精 size=1^見 = 2R/v 見 et la probabilité par l’unité de temps d’émission de la particule 見 est = (1/ 精 size=1^見)⁰, où ⁰ est le coefficient de transmission de la barrière. Le calcul de ⁰, assez complexe, ne présente pas de difficulté de principe:

où B est la hauteur de la barrière, U la valeur du puits de potentiel dans le noyau et Z le numéro atomique du noyau.

Si la barrière n’intervenait pas (T⁰ = 1), la vie moyenne des émetteurs 見 serait de l’ordre 精 size=1^見 = 10^-19 s. On constate que ⁰ dépend essentiellement du rapport E/B. Pour les noyaux lourds, une variation de 1 MeV de l’énergie E produit une variation de la vie moyenne égale à 10⁵ fois environ sa valeur. De même, une augmentation de 10 p. 100 du rayon du noyau, qui conduit à une valeur plus faible de B, multiplie par un facteur d’environ 150. La «transparence» de la barrière de potentiel est l’élément fondamental qui détermine les énormes variations de période d’un nuclide à un autre (tabl. 1).

Alors que les énergies des particules 見 émises varient d’un facteur 4, le facteur 1/ 精見 varie d’un facteur 40 et les périodes d’un facteur 10³⁰. Les expressions ci-dessus permettent d’obtenir les relations correctes entre les divers paramètres: énergie, période, rayon du noyau, etc., et remplacent une relation empirique établie en 1911 par Geiger et Nuttal.

Lorsque le moment angulaire de la particule 見 par rapport au noyau n’est pas nul (l 0), l’expression donnant la hauteur de la barrière de potentiel contient un terme de la forme:

où r est la distance de la particule 見 au noyau, et il faut en tenir compte dans les calculs précis qui interviennent lorsqu’on cherche à comparer l’intensité mesurée des raies de structure fine avec la théorie. Cette théorie est d’autre part fondée sur l’hypothèse que la particule 見 est préformée à l’intérieur du noyau, ce qui est probablement inexact. L’expérience montre en effet que les probabilités sont souvent plus faibles que celles qu’on peut calculer. On rend compte de cela en introduisant un facteur d’interdiction, dont l’explication n’est pas encore bien comprise et qui fait l’objet de recherche.

3. Fission spontanée

On appelle fission spontanée le processus par lequel un noyau de nombre de masse A et de charge Z se scinde en deux fragments approximativement égaux. Énergétiquement, le processus est possible, le bilan énergétique étant de l’ordre de 200 MeV. Pour un noyau de nombre de masse A égal à 240 par exemple, l’énergie moyenne de liaison par nucléon est de 7,6 MeV; s’il se transforme en deux noyaux de masse A¹ = 100 et A² = 140, pour lesquels les énergies moyennes de liaison sont 8,6 et 8,4 MeV respectivement, l’énergie libérée est:

On obtient plus d’informations en utilisant une formule donnant la masse exacte des noyaux ^{[cf. NOYAU ATOMIQUE]}. Dans le cas où le noyau (A, Z) se partage en deux noyaux identiques (A/2, Z/2), l’énergie libérée est donnée par:

où M(A, Z) est la masse du noyau (A, Z), d’où:

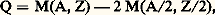
pour A 力 240 et Q 力 170 MeV (a ^s et a ^c sont des paramètres définis dans l’article NOYAU ATOMIQUE). Cette énergie provient de la variation de deux termes: augmentation de l’énergie de surface (face=F0019 力 130 MeV) et diminution de l’énergie coulombienne (face=F0019 力 300 MeV). Comme pour l’émission 見, qui est aussi un mode de partition du noyau en deux fragments très inégaux, c’est un effet de barrière de potentiel qui maintient le noyau (A, Z) en équilibre. La figure 5 représente les variations de l’énergie mutuelle de deux fragments identiques en fonction de leur distance, R étant le rayon d’un fragment. On calcule aisément la hauteur de la barrière coulombienne B à la distance 2 R lorsque les deux fragments sont en contact; en réalité, la barrière effective est moins haute en raison de l’intervention des forces nucléaires et a une valeur E^H. On peut connaître la différence (E^H 漣 Q) en apportant au noyau l’énergie nécessaire pour provoquer la fission: cette énergie est de l’ordre de quelques méga-électrons-volts pour les noyaux très lourds.

Les périodes partielles de fission spontanée sont de l’ordre de 10¹⁶ ans pour les nuclides tels que l’uranium et le thorium (fig. 6). Elles décroissent rapidement en fonction de la valeur de Z²/A, rapport appelé souvent paramètre de fission.

L’extrapolation de la droite de la figure 6 conduit à un ordre de grandeur de la limite de stabilité des noyaux. En effet, pour les noyaux de plus en plus lourds que l’on cherche à produire artificiellement, le paramètre de fission croît, et la différence (Q 漣 B) décroît. Diverses estimations conduisent à penser que, pour Z²/A 閭 44, un noyau est instable vis-à-vis de la fission spontanée (période 力 10^-20 s). En fait, dans cette théorie, on n’a pas tenu compte des effets de structure nucléaire qui peuvent conduire à modifier cette limite.

4. Émission size=5廓

Les noyaux sont capables d’émettre des particules chargées négativement qui ont été identifiées comme des électrons, par leur rapport e /m en particulier. Deux autres types de radioactivité 廓 sont connus: l’émission de positrons et la capture d’un électron orbital. Les transformations sont isobariques et seul le numéro atomique du noyau change d’une unité. L’énergie de l’électron émis n’ayant pas une seule valeur possible, mais un spectre continu de valeurs jusqu’à une valeur maximale, la question d’une non-conservation de l’énergie dans le processus d’émission 廓 s’est posée initialement. L’hypothèse, puis la découverte d’une particule neutre appelée neutrino, émise en même temps que l’électron ^{[cf. NEUTRINOS]}, ont montré que l’énergie est effectivement conservée lors de la désintégration 廓. On peut donc représenter le processus d’émission 廓 par le schéma suivant:

où les symboles 益 et 益 représentent respectivement le neutrino et l’antineutrino. Il y a émission 廓 lorsque la somme des masses des éléments du premier membre est supérieure à celle qui est relative au second membre. Les noyaux sont composés uniquement de protons et de neutrons et les particules 廓 et les neutrinos ne sont créés qu’au moment de l’émission. Cela indique que l’émission 廓 doit être traitée comme un processus radiatif. Fermi a formulé une théorie analogue à celle de l’interaction électromagnétique. Les périodes de radioactivité 廓 sont longues par rapport aux périodes correspondant à l’émission 塚, ce qui signifie que l’interaction 廓 est relativement faible.

Lois de conservation dans l’émission size=5廓

Le neutrino émis en même temps que l’électron a des caractéristiques telles que les lois de conservation de la charge, de l’énergie et du moment cinétique sont vérifiées dans l’émission 廓; en effet, le neutrino n’est pas chargé et emporte l’énergie et le moment angulaire complémentaire de ceux de l’électron. Enfin, particule de spin 1/2, il obéit à la statistique de Fermi-Dirac, en accord avec le principe de conservation de statistique: les deux isobares contenant le même nombre de nucléons (fermions) obéissent à la même sorte de statistique, et, puisque la particule 廓 est un fermion, le neutrino doit en être un aussi (cf. NEUTRINO et PARTICULES ÉLÉMENTAIRES).

Yang et Lee ont suggéré que la parité peut ne pas être conservée dans les interactions faibles, c’est-à-dire que l’image dans un miroir de la situation expérimentale ne correspond pas à une situation expérimentale identique. Cette hypothèse a été vérifiée par plusieurs expériences: en particulier, Wu et ses collaborateurs, en mesurant la distribution angulaire d’électrons provenant de désintégrations 廓 de noyaux de ⁶⁰Co polarisés, ont trouvé une dissymétrie pour les angles et 神 漣 . De plus, on a mis en évidence le fait que les électrons issus d’une source non polarisée possèdent une polarisation longitudinale: les électrons sont en prédominance dans un état de spin antiparallèle à la direction du mouvement, et les positrons sont en prédominance dans un état de spin parallèle à cette direction. Ces résultats montrent que l’invariance demeure, à condition que l’image dans un miroir d’une particule soit son antiparticule.

Divers types de transition size=5廓

La paire électron-neutrino possède un moment angulaire de la forme L + S, où L = l ^e + l ^v est le moment orbital total et où S = S^e + S^v est le moment intrinsèque total. Chaque fois que l ^e ou l ^v 礪 0 est nécessaire pour assurer la conservation du moment angulaire, le processus est retardé par les effets centrifuges.

Une particule de moment angulaire l doit être créée à une distance moyenne r du noyau de l’ordre de l 寮/p = l, relation où p représente la quantité de mouvement et =/2 神 la longueur d’onde associée à la particule.

Il est difficile, pour une source confinée dans une sphère de rayon R, d’exciter une onde avec l 礪 R/.

L’intensité excitée doit ainsi diminuer d’un facteur de l’ordre de (R/)² pour chaque unité de moment angulaire. Expérimentalement, les transitions les plus rapides correspondent en effet à une variation I du moment angulaire du noyau inférieure ou égale à 1 ( I 諒 1), et les transitions avec I 礪 1 sont retardées par rapport aux premières. En effet, I 礪 1 nécessite l ^e ou l ^v 0, mais I = 1 peut correspondre à L = 0 et S = 1. Les transitions sont classées en «permises» et «interdites». Les dernières transitions sont retardées soit par une valeur L 礪 0, soit par un changement de parité des états nucléaires initial et final.

Les règles de sélection pour les transitions permises sont:

Les transitions permises sont enfin classées en composantes singulet et triplet pour lesquelles les spins des leptons sont respectivement antiparallèles (S = 0) et parallèles (S = 1).

L’état singulet permis n’est donc seulement formé que lorsque I = 0, avec I^f = Iⁱ (règle de sélection de Fermi). L’état triplet correspond à I = 0 ou 1, c’est-à-dire I^f = Iⁱ ou I^f = Iⁱ 梁 1 (règle de sélection de Gamov-Teller).

Dans le cas des transitions permises, le spectre de l’énergie de l’électron émis est dit «à forme statistique»; en effet, à part la distorsion coulombienne introduite par un facteur F(Z), la dépendance en énergie provient de la proportionnalité à l’espace des phases disponible:

où p et q représentent les quantités de mouvement de l’électron et du neutrino émis. Pour vérifier cette dépendance, on construit des diagrammes de Kurie qui représentent la quantité [N 梁(W)/p WF]^1/2 en fonction de l’énergie W. Dans cette expression, N 梁 est le nombre d’électrons ou de positrons dont l’énergie se situe dans une bande centrée sur W. La théorie prévoit que c’est une droite coupant l’axe des abscisses à l’énergie maximale W⁰. Expérimentalement, on constate toujours un excès d’électrons pour les basses énergies à cause de la diffusion et de l’absorption des 廓 dans les matériaux entourant la source et dans la source elle-même. En corrigeant le spectre de l’ensemble de détection par des électrons mono-énergétiques de diverses énergies, on obtient effectivement des droites jusqu’à une très basse énergie (fig. 7).

Capture électronique

Au cours du processus de capture électronique, un électron atomique interagit avec un proton pour former un neutron et un neutrino. Le neutrino reçoit toute l’énergie libérée dans la transition, mis à part la petite énergie de recul du noyau. Il est pratiquement impossible de détecter le neutrino, et la capture électronique n’est mise généralement en évidence que par les effets atomiques (émission de rayons X, d’électrons Auger) qui suivent la création d’un trou dans la couche K ou L.

La théorie de la capture électronique est semblable à celle de l’émission 廓.

5. Émission size=5塚 et conversion interne

Description de l’émission size=5塚

Les noyaux ^{[cf. NOYAU ATOMIQUE]} possèdent des états excités caractérisés en particulier par leur énergie, leur moment angulaire et leur parité. Les noyaux dans un état d’excitation élevée perdent leur énergie généralement par l’émission d’une particule lourde (neutron, proton, particule 見, etc.). Au-dessous de l’énergie de séparation de la particule la moins liée, la désexcitation est de type électromagnétique: émission de rayonnement 塚 ou conversion interne.

Dans un processus de désexcitation électromagnétique Kurie, le noyau retombe dans un état moins excité ou dans son état fondamental. Le phénomène est analogue à l’émission de lumière par les atomes excités, mais les énergies des quanta électromagnétiques émis par les noyaux sont 10⁴ à 10⁶ fois plus grandes que celles d’un photon dans le visible.

Une description complète de l’émission d’un rayonnement électromagnétique par un système quantique fait nécessairement appel à la théorie quantique du rayonnement. Les rayonnements sont classés d’après le moment angulaire l transporté par chaque quantum. Pour un l donné, il y a deux types possibles de rayonnement: électrique 2^l polaire (E^l ), et magnétique 2^l polaire (M^l ), suivant que la parité du vecteur champ magnétique est (face=F0019 漣 1)^l ou (face=F0019 漣 1)^l-1 . Classiquement, les rayonnements E^l et M^l sont émis par un multipôle d’ordre l électrique ou magnétique.

La conservation du moment angulaire et de la parité pour le système du noyau et des rayonnements impose des règles de sélection pour les transitions possibles entre deux états (Jⁱ , 神ⁱ ) et (J^f , 神^f ):

respectivement pour un rayonnement E^l et pour un rayonnement M^l .

La détermination des énergies et des multipolarités des rayonnements émis par un noyau dans un état excité permet d’établir le schéma de niveaux du noyau. De plus, les probabilités de transition 塚 dépendent de façon très sensible des fonctions d’onde des états et peuvent ainsi servir à vérifier la validité des modèles nucléaires.

Probabilité de transition pour un proton

La probabilité de transition pour un proton entre un état initial i et un état final f se calcule, en mécanique quantique, par la théorie des perturbations. On obtient la relation:

où H représente l’interaction de perturbation, où 麗 f |H|i 礪 est l’élément de matrice de cette interaction pris entre les fonctions d’onde des états initial et final et où la densité d’états finals par unité d’énergie s’exprime par d Nd E.

Au premier ordre, le hamiltonien d’interaction est:

où 靖 est le vecteur de spin, p l’opérateur de moment de valeur i 寮 grad., A le potentiel vecteur et H le champ magnétique.

Les règles de sélection proviennent des conditions nécessaires pour que les éléments de matrice ne s’annulent pas. Elles sont:

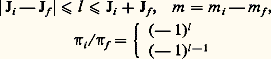
respectivement pour E et pour M.

Une transition entre deux états de moments angulaires donnés peut se faire en principe par émission de tous les rayonnements de multipolarités permises. En réalité, elle se fait essentiellement par le multipôle le plus bas, qui est aussi le plus probable. Des modèles nucléaires plus élaborés prédisent un mélange des multipôles les plus bas (tabl. 2).

La probabilité de transition totale est obtenue en faisant la somme des probabilités pour tous les sous-états m de l’état final f et en prenant la moyenne correspondant à tous les sous-états m de l’état initial i .

Si l’on considère que les protons se déplacent dans un potentiel central, chacune de leurs fonctions d’onde peut s’écrire comme le produit d’une fonction d’onde radiale qui dépend du potentiel et d’une fonction d’onde qui dépend des angles et des spins. En supposant que la fonction d’onde radiale est constante dans le noyau, et nulle à l’extérieur du noyau, on obtient les estimations indiquées dans la figure 8, pour les périodes de désexcitation par transition d’un proton.

Les résultats pour les transitions d’un seul neutron sont différents de ceux qui apparaissent sur la figure 8, et en particulier la probabilité de transition électrique est très réduite, puisque le neutron n’est pas chargé; elle n’est cependant pas nulle à cause du mouvement orbital du reste du noyau autour du centre de gravité de tout le noyau.

Expérimentalement, on ne trouve pas de différence systématique entre transitions de neutron et de proton. D’autre part, les écarts avec la théorie atteignent plusieurs ordres de grandeur. Cela indique que les états excités des noyaux ne peuvent être bien décrits en termes de pures excitations de particules indépendantes.

Conversion interne

La conversion interne est le processus par lequel l’énergie d’excitation du noyau, au lieu d’être émise sous forme de photon, est transférée directement à un électron du cortège des couches K, L, M, etc. Elle est toujours en compétition avec l’émission 塚. L’énergie et le moment angulaire disponibles sont transférés à l’électron qui est émis avec une énergie cinétique E^e = E size=1^塚 漣 B, si l’on désigne par B l’énergie de liaison dans la couche K, L, M, etc.

Le rapport de la probabilité de transition par conversion interne à la probabilité de transition par émission 塚 s’appelle coefficient de conversion interne 見, avec 見 = 見^K + 見^L + 見^M + ..., étant donné que 見^K, 見^L, 見^M, etc. sont les coefficients de conversion dans les couches K, L, M, etc. Les électrons émis sont mono-énergétiques et apparaissent sous forme de raies dans un spectrographe (fig. 9). Ces raies permettent une mesure précise de l’énergie des transitions et constituent l’un des outils essentiels de la spectroscopie nucléaire.

Dans le processus de conversion interne, l’état initial consiste en un noyau ayant une certaine énergie d’excitation et en un électron dans son état fondamental; l’état final comporte un noyau ayant perdu son énergie d’excitation et un électron dans le continuum. Le mécanisme met en jeu deux états intermédiaires pour lesquels une seulement des deux particules a fait sa transition vers l’état final. Des calculs de coefficients de conversion ont été faits par plusieurs auteurs (fig. 10).

Les fonctions d’onde nucléaire qui interviennent dans la conversion interne sont les mêmes que dans l’émission 塚, et les coefficients de conversion ne dépendent que de l’énergie de la transition, du numéro atomique de l’émetteur, de la couche ou sous-couche d’où est éjecté l’électron, de la multipolarité du rayonnement 塚 en compétition et du caractère électrique ou magnétique de la transition nucléaire.

Le fait qu’à une très bonne approximation près les coefficients de conversion ne dépendent pas de la structure nucléaire permet souvent de déterminer la nature et la multipolarité de la transition par une mesure du coefficient de conversion.

Une autre méthode consiste à mesurer la distribution angulaire pour des noyaux alignés ou les corrélations angulaires entre rayonnements successifs.

6. Émission d’un nucléon

Les émissions de particules lourdes (particules 見, protons, neutrons) se produisent lorsque les noyaux sont très lourds, lorsqu’ils sont très riches ou très pauvres en neutrons ou lorsqu’ils sont très excités. L’énergie de liaison du dernier neutron devient négative au-delà d’un certain nombre de neutrons et les noyaux correspondants ne peuvent exister. En revanche, il arrive que l’émission 廓 d’un noyau instable conduise à un état excité du noyau fils tel que l’énergie d’excitation soit supérieure à l’énergie de liaison du dernier neutron qui est alors émis immédiatement. La désintégration a la période de l’émission 廓 et le phénomène apparaît comme l’émission d’un neutron retardé, d’où l’expression de radioactivité par neutron différé.

L’émission d’un proton par un noyau pauvre en neutrons est possible si l’énergie de liaison du dernier proton est négative. Elle présente une certaine analogie avec l’émission 見; en particulier, elle est retardée par la barrière centrifuge et la barrière coulombienne. L’émission d’un proton peut aussi avoir lieu à partir d’un état excité atteint par désintégration 廓, et, si les conditions énergétiques sont satisfaites, elle suit alors la période de l’émission 廓.

Les études sur la radioactivité ont, pour une très grande part, contribué à la connaissance de la structure des noyaux atomiques. Elles servent en particulier à préciser l’organisation et l’interaction des nucléons dans la matière nucléaire. De plus, on sait qu’il existe quatre cent cinquante nuclides stables, auxquels il faut ajouter plus de mille huit cents nuclides radioactifs aujourd’hui connus (en 1982). Les prévisions sur la stabilité permettent d’envisager l’existence de plus de deux mille nuclides encore inconnus.

7. Radioactivité dans la nature

La radioactivité naturelle est essentiellement due à des radionuclides de très longue période, de l’ordre de l’âge de la terre (4,6 milliards d’années), sinon ils auraient déjà disparu, ainsi qu’à leurs descendants radioactifs, qui peuvent exister avec des périodes plus courtes puisqu’ils sont constamment renouvelés.

Il faut citer essentiellement les trois familles (cf. fig. 1) de l’uranium 238 (4,5 憐 10⁹ ans), de l’uranium 235 (7,1 憐 10⁸ ans) et du thorium 232 (1,4 憐 10¹⁰ ans), ainsi que l’isotope 40 du potassium (1,3 憐 10⁹ ans, 0,012 p. 100 du potassium naturel), émetteur 廓 size=1^漣, sans descendant radioactif. Incidemment, la faiblesse relative de la période de l’uranium 235 explique sa faible concentration (0,7 p. 100) dans l’uranium naturel, qui, pour la majorité des réacteurs actuellement en service, nécessite un enrichissement en isotopes 235. Cette concentration était de 3 p. 100 il y a près de deux milliards d’années, analogue à celle de l’uranium enrichi utilisé dans nos centrales électronucléaires, et elle a permis à cette époque le fonctionnement de réacteurs naturels découverts à l’état fossile au Gabon dans la mine d’uranium d’Oklo en 1972.

La concentration massique moyenne de ces radionuclides dans la croûte terrestre est faible et se chiffre en parties par million. Néanmoins, ce sont des sources permanentes d’énergie, et l’énergie qu’ils dégagent est un des facteurs du bilan géothermique du globe terrestre ^{[cf. GÉOTHERMIE]}.

En dehors de ces nuclides naturels de périodes de l’ordre de l’âge de la terre, il en existe de périodes encore plus longues et de ce fait très faiblement actifs. On peut citer parmi d’autres le rubidium 87 (4,7 憐 10¹⁰ ans), le lanthane 138 (1,3 憐 10¹¹ ans), émetteurs 廓 size=1^漣, le samarium 147 (1,1 憐 10¹¹ ans), le platine 190 (6,1 憐 10¹¹ ans), émetteurs 見.

D’autres nuclides sont formés en permanence par l’interaction du rayonnement cosmique avec l’atmosphère et même avec le sol. Ils peuvent donc aussi exister à l’état naturel avec des périodes courtes vis-à-vis de l’âge de la terre. Le principal est le carbone 14, de période 5 700 ans, dont la décroissance est utilisée pour dater les matériaux carbonés anciens.

La présence de radionuclides dans le sol, les matériaux de construction, l’atmosphère (cf. le radon 222, de période 3,8 jours, descendant gazeux de l’uranium 238) créent à la surface de la terre un environnement de rayonnements auquel vient s’ajouter le rayonnement cosmique. Cet environnement varie selon les régions. La variation porte très couramment sur un facteur de quelques unités entre régions voisines; elle atteint un facteur dix ou plus entre les régions les plus et les moins radioactives. Le corps humain contient organiquement du potassium 40 et du carbone 14 qui contribuent environ au quart des doses de rayonnements qu’il reçoit de son environnement dans les régions les moins radioactives.

• 1896; de radioactif

n. f. émission, par certains éléments, de rayonnements divers, résultant de réactions nucléaires.

Encycl. Phys. - Un élément radioactif est caractérisé par sa période (temps pendant lequel la moitié de ses noyaux s'est désintégrée) et par son activité (nombre de désintégrations par unité de temps), laquelle s'exprime en curies (symbole Ci); 1 Ci = 3,7.10 10 désintégrations par seconde; c'est l'activité d'un gramme de radium. La mesure de l'activité d'un corps radioactif permet de déduire le temps depuis lequel ce corps se désintègre et, en partic., de procéder à la datation d'échantillons, à condition que la période du radioélément retenu ne soit pas trop courte par rapport à l'âge à déterminer. Ainsi, le carbone 14, dont la période est de 5 600 ans, permet de mesurer des âges allant jusqu'à 50 000 ans et le potassium 40 jusqu'à 80 millions d'années. Les corps radioactifs agissent sur l'organisme par irradiation (action des rayonnements) ou par contamination (inhalation, ingestion ou contamination externe). Ils provoquent des ionisations entraînant des modifications biochimiques plus ou moins graves. La dose de rayonnements reçus est exprimée en röntgens ou en rems (des lésions apparaissent en général au-delà de 50 rems). L'effet destructeur des irradiations sur les organismes vivants est utilisé pour traiter certaines tumeurs (radiothérapie), pour stériliser les denrées alimentaires (lait, viande, etc.) et pour créer, par mutation, de nouvelles espèces (horticulture, agronomie). tabl. éléments.

⇒RADIOACTIVITÉ, RADIO-ACTIVITÉ, subst. fém.

A. — Propriété que possèdent à des degrés divers, certains corps radioactifs; p. méton., manifestation de cette propriété. Contrôle, mesure de la radioactivité. Mais des substances dépourvues de radioactivité, comme le caesium, produisent le même effet (ROGER ds Nouv. Traité Méd. fasc. 6 1925, p. 47):

• D'après certaines observations, la neige fraîchement tombée est radioactive. Pour ma part, je n'ai pu déceler aucune trace de radioactivité dans les différentes substances que j'ai étudiées dans l'Antarctique: pluie, neige, givre, grésil, verglas.

ROUCH, Régions polaires, 1927, p. 173.

♦ Radioactivité artificielle. Radioactivité obtenue en bombardant des particules (protons, neutrons, etc.). On a admis en principe que la radioactivité artificielle résultant de l'action de l'homme, peut être égale à la radioactivité naturelle (COLAS-CAB. 1968).

♦ Radioactivité naturelle. Radioactivité manifestée par certains noyaux lourds instables, existant à l'état naturel. L'homme est soumis à la radioactivité naturelle à laquelle s'ajoute la radioactivité artificielle (examens radiologiques, retombées radioactives, contamination par déchets nucléaires, etc.) (Hachette 1980).

— P. métaph. « J'essaierai, je vous le jure », dit-elle après un silence, vaincue par l'espèce de radio-activité qui émanait de cet homme supérieur (BOURGET, Geôle, 1923, p. 76). Le grec et le latin nous les raniment [nos racines étymologiques] tout entières dans leur fraîcheur, dans leur vivacité, dans leur lumière, dans leur radioactivité souveraine (L. DAUDET, Ét. et mil. littér., 1927, p. 121).

B. — P. méton. Science qui étudie cette propriété. Certains pensaient que (...) [l'on] en était (...) [arrivé] au stade où seuls des travaux de précision restaient à réaliser. C'est alors qu'on assista à un nouvel essor de la radioactivité et de la physique nucléaire (Hist. gén. sc., t. 3, vol. 2, 1964, p. 343).

Prononc. et Orth.:[]. Att. ds Ac. 1935. Étymol. et Hist. 1898 (C.r. de l'Ac. des sc., t. 127, p. 1216). Comp. de radio-¹ et de activité. Fréq. abs. littér.:59.

radioactivité [ʀadjoaktivite] n. f.