Akademik

ÉLASTICITÉ

La théorie de l’élasticité est la théorie des petites déformations continues et réversibles des milieux isotropes élastiques. Elle donne, en principe et moyennant certaines hypothèses, la solution théorique complète des problèmes posés en résistance des matériaux, dont elle tend de plus en plus à se rapprocher après en être restée tout d’abord indépendante. Les calculs auxquels cette théorie conduit ne peuvent être explicités que dans des cas relativement simples; dans les autres cas, on les simplifie en recherchant une première approximation de la solution mathématique rigoureuse (théorie des liaisons élastiques parfaites entre solides supposés indéformables, par exemple). Enfin, on fait appel à l’expérience soit pour vérifier les résultats des méthodes théoriques précédentes et les préciser lorsque leur approximation est insuffisante, soit pour les suppléer lorsqu’elles sont impuissantes, et, de toute façon, pour déterminer les caractéristiques élastiques intrinsèques des matériaux utilisés.

La théorie de l’élasticité suppose que les matériaux étudiés possèdent les trois propriétés suivantes:

– Tout d’abord, ils sont parfaitement élastiques (si les forces extérieures qui provoquent leur déformation ne dépassent pas une certaine limite, celle-là disparaît en même temps que la force qui lui a donné naissance). Les matériaux possèdent cette propriété à un degré variable en pratique.

– Ensuite, ils sont homogènes et distribués uniformément dans tout le volume qu’ils occupent, de telle sorte que le plus petit élément détaché d’un corps donné possède les mêmes propriétés physiques que le corps tout entier.

– Enfin, ils sont isotropes, c’est-à-dire que leurs propriétés élastiques sont les mêmes dans toutes leurs directions. Les matériaux utilisés dans les constructions ne satisfont pas en général, dans leur ensemble, à cette dernière hypothèse; ils sont en effet constitués souvent de cristaux (acier par exemple) de formes diverses et différemment orientés. Cependant, les théories générales de l’élasticité, quoique fondées sur l’homogénéité et l’isotropie, donnent des résultats tout à fait valables. En effet, tant que les dimensions globales des corps envisagés sont considérables par rapport à celles des cristaux, l’hypothèse de l’homogénéité est parfaitement justifiée. De plus, l’hypothèse de l’isotropie se trouve justifiée, elle aussi, puisque les cristaux se trouvent naturellement distribués au hasard dans la matière. Cependant, lorsque, à la suite de certains traitements industriels, le laminage par exemple, les cristaux s’orientent dans une direction bien déterminée, ils ne sont plus distribués au hasard, et les corps doivent alors être considérés comme anisotropes.

1. Tenseur des contraintes

Dans tout ce qui suit, les corps étudiés seront repérés par rapport à un système d’axes cartésiens orthogonaux (Ox ¹x ²x ³), mais toutes les équations écrites resteront valables dans les autres systèmes de coordonnées. Les correspondances d’un système donné dans un autre figurent dans les ouvrages spécialisés indiqués dans la bibliographie. Dans le système d’axes orthogonaux (Ox ¹x ²x ³), on utilisera, pour alléger l’écriture, la convention de l’indice muet et celle de l’indice franc. Soit, par exemple, A¹, A², A³ les projections sur les axes Ox ¹, Ox ², Ox ³ d’un vecteur だ; la convention de l’indice muet consiste, lorsqu’un indice littéral est répété deux fois dans un monôme, à remplacer ce dernier par la somme de tous les termes obtenus en donnant à cet indice les valeurs 1, 2, 3 dans ce monôme. Ainsi Aⁱ Bⁱ représente la somme

c’est-à-dire le produit scalaire des vecteurs だ et ち. Un indice non muet est dit franc; il ne peut apparaître qu’une seule fois dans un même monôme. Ainsi, dans Aⁱ = L^ij B^j , i est un indice franc et j est muet, et cette formule représente, en fait, les trois égalités classiques

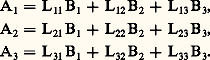
Toujours par souci de concision, on notera par une virgule suivie d’un indice une dérivée partielle. Ainsi, A^2,3 désigne la dérivée partielle 煉A²/ 煉x ³ de A² par rapport à x ³.

Définition des efforts intérieurs de cohésion

Considérons un corps (S) en équilibre sous l’action d’un système de forces extérieures づ¹... づⁿ données (fig. 1) qui sont soit des forces réparties sur tout ou partie de la surface extérieure de (S), soit des forces de volume (pesanteur, champ électromagnétique, etc.). Dans ces conditions, des efforts intérieurs à (S) doivent être pris en considération, comme le montre l’analyse suivante. Coupons le corps (S) en deux parties (S¹) et (S²), par une frontière ( ) passant par M; soit ょ le vecteur unitaire normal à ( ) en M dirigé vers l’extérieur de (S¹), c’est-à-dire vers l’intérieur de (S²). Pour que l’équilibre de (S¹) ne soit pas détruit par la coupure sous l’effet des forces づⁱ⁺¹ ... づⁿ agissant sur lui, des actions réparties sur ( ) doivent être exercées par (S²) sur (S¹), ces actions étant dues aux forces づ¹... づⁱ agissant sur (S²). On admet que ces actions sont des actions de contact et que leur répartition sur ( ) est continue. Elles sont donc représentées par un champ de forces défini sur ( ) ayant, en chaque point de ( ), une densité superficielle de forces notée び. Ce vecteur び ne dépend que de M et de ょ, on l’écrit び (M, ょ) et il est fonction, a priori, de cinq paramètres: les trois coordonnées de M et les paramètres fixant la direction de ょ. Le vecteur び (M, ょ) s’appelle le vecteur contrainte en M pour la direction ょ ou vecteur contrainte en M sur une facette normale à ょ. Le scalaire ょ 練 び (M, ょ) = Tⁿ est la contrainte normale en M pour la direction ょ ou sur une facette normale à ょ. Si Tⁿ est positif, on dit qu’au point M, et pour la direction ょ, le matériau subit une tension ; si Tⁿ est négatif, on dit qu’il subit une compression. Le vecteur

est la contrainte tangentielle en M ou contrainte de glissement ou de cisaillement pour la direction ょ au point M.

Introduction du tenseur des contraintes

On peut écrire la loi fondamentale de la dynamique pour un domaine ( 行) intérieur à (S) limité par une surface ( ) fermée. Soit, à l’instant considéré, ゔ (M) l’accélération d’un point M de (S). Supposons que les forces données extérieures à (S) et s’exerçant sur ( 行) soient définies par une densité volumique み (M); il ne peut pas, en effet, y avoir de telles forces extérieures de surface appliquées sur ( 行), puisque ( 行) est intérieur à (S) et les seules forces de surfaces agissant sur ( 行) sont des contraintes. La loi fondamentale appliquée à ( 行) dans le repère (Ox ¹x ²x ³) absolu ou non (dans ce dernier cas み(M) comprend les forces d’inertie d’entraînement et complémentaires) se traduit par:

où d 靖 est un élément d’aire de ( ) et où d 猪 et dn sont respectivement la masse et le volume élémentaires en un point quelconque M de ( 行) (d 猪 = 福 dv si 福 est la masse volumique). Si, en particulier, on fait ゔ = dans ces deux équations, le corps considéré est en équilibre; l’équation (1) indique que la somme des forces appliquées à ( 行) est nulle, l’équation (2) que la somme des moments de ces forces au point O est nulle.

L’application de l’équation (1) au domaine ( 行) particulier constitué par un tétraèdre ayant pour sommet O et trois des faces dans les plans de coordonnées (fig. 2) permet d’écrire les contraintes en un point M de la face quelconque ABC de ( 行) ayant pour normale ょ; on obtient ainsi び (M, ょ) = Tⁱ や ⁱ avec Tⁱ = 靖^ij n ^j . Les neuf 靖^ij sont des nombres et les やⁱ sont les vecteurs unitaires や¹, や² et や³ du repère (Ox ¹x ²x ³). Les quantités 靖^ij sont les composantes des contraintes en M, mais sur des facettes parallèles aux plans x ²x ³, x ³x ¹, x ¹x ². Connaissant les 靖^ij , les relations び (M, ょ) = びⁱ size=1^やi et Tⁱ = 靖^ij n ^j (où les n ^j sont les cosinus directeurs de ょ) permettent de calculer les composantes de la contrainte agissant sur tout plan quelconque passant par M, quelle que soit son inclinaison (le plan ABC par exemple). Ainsi, les composantes de び (M, ょ) sont des formes linéaires et homogènes des composantes de ょ, et l’opérateur linéaire faisant passer de ょ à び, tenseur du second ordre, est appelé tenseur des contraintes en M et noté 暈. Dans le système d’axes (Ox ¹x ²x ³), ce tenseur est défini par les composantes 靖^ij , qui sont les éléments de la matrice ( 靖^ij ), les indices i et j désignant respectivement les numéros des lignes et des colonnes. Le tenseur 暈 varie avec le point M considéré; on a donc, en fait, un champ de tenseurs défini sur le solide. Si le tenseur est indépendant de M, on dit que le champ des contraintes est homogène.

Les 靖^ij étant les composantes des contraintes en M sur des facettes parallèles aux plans de coordonnées, on peut les représenter graphiquement sur les faces d’un cube élémentaire parallèles à ces plans (fig. 3). Pour les faces du cube élémentaire perpendiculaires à l’axe Ox ², par exemple, la composante normale de la contrainte est désignée par 靖²² et ses deux composantes tangentielles par 靖²³ et 靖²¹. D’une manière générale, la composante 靖^ij est celle agissant sur la face perpendiculaire à l’axe Ox ⁱ et dirigée suivant l’axe Ox ^j . Toutes les composantes pour lesquelles i = j sont donc des contraintes normales.

La matrice ( 靖^ij ) associée au tenseur 暈 est écrite en (3) du tableau 1. Parfois, les contraintes normales sont notées 靖 (comme dans ce texte) mais les contraintes tangentielles sont notées 精 pour éviter les confusions. On n’emploiera pas cette notation ici pour alléger l’écriture. La relation び (M, ょ) = ( 靖^ij n ^j ) やⁱ développée en (4) permet de calculer les composantes de la contrainte び (M, ょ) sur toute facette de normale unitaire ょ, les composantes de ょ étant n ¹, n ² et n ³ sur les axes Ox ¹, Ox ², Ox ³.

Équations de l’équilibre ou du mouvement

En supposant qu’à l’instant considéré ゔ est identiquement nul, on obtient les trois équations d’équilibre f ⁱ + 靖^{ij ,j} = 0 écrites en une seule avec la convention de l’indice muet (i , j = 1, 2, 3). Dans le cas où ゔ n’est pas nul, il y a mouvement et l’on obtient 福塚ⁱ = f ⁱ + 靖^{ij ,j} . Ces relations développées en (5) tiennent compte de la réciprocité des cisaillements 靖^ij = 靖^ji .

Symétrie du tenseur des contraintes

L’équation (2) conduit à 靖^ij = 靖^ji ; c’est la relation fondamentale de la réciprocité des cisaillements: le tenseur 暈 est, dans tous les cas, un tenseur symétrique. Ainsi, les efforts intérieurs sont définis à partir d’un champ de tenseurs symétriques du second ordre, c’est-à-dire à partir de six, et non plus neuf, fonctions inconnues 靖^ij des trois coordonnées du point M et ces six fonctions sont liées par les trois équations d’équilibre ou les trois équations du mouvement précédentes. La deuxième matrice ( 靖^ij ) écrite en (4) tient compte de cette symétrie.

Étude du tenseur des contraintes en un point

Supposons que l’on étudie le tenseur des contraintes en un point O pris comme origine des coordonnées et considérons une facette tournant autour de O. Pour chaque position de cette facette, il existe un vecteur normal unitaire ょ en O défini par la convention précédemment explicitée. Considérons un vecteur OPde même direction que ょ et de longueur OP = r / 連|Tⁿ |, r étant un facteur constant d’homogénéité. Les coordonnées de l’extrémité de OPsont n ¹ 練 OP, n ² 練 OP, n ³ 練 OP et, lorsque ょ varie, on trouve que l’ensemble des points réels P admet pour équation 靖^ij x ⁱ x ^j = size=1^梁 r ², ce qu’on a écrit sous forme développée en (6). Les points P se situent sur la quadrique des contraintes au point O qui est complètement déterminée par les conditions de contrainte au point O. Si l’on modifie la direction des axes de coordonnées (le point O demeurant fixe), la surface en question restera invariable et seules seront modifiées les composantes 靖^ij de la contrainte, c’est-à-dire les coefficients de l’équation (6). Il existe alors un trièdre trirectangle (OX¹X²X³), dit repère principal en O par rapport auquel les termes rectangles de (6) sont nuls, c’est-à-dire tel que 靖²³ = 靖³¹ = 靖¹² = 0; la matrice ( 靖^ij ) donnant les composantes du tenseur 暈 est alors diagonale. Dans ce repère particulier, les seules contraintes qui subsistent sont les contraintes normales (perpendiculaires aux trois plans principaux de contrainte X²X³, X³X¹, X¹X² sur lesquels elles agissent) 靖¹¹, 靖²², 靖³³ qui sont notées, dans ce cas particulier, 靖¹, 靖² et 靖³ et appelées contraintes principales en O. Les directions principales sont telles que ょ et び (O, ょ) soient colinéaires; autrement dit, une direction est principale si, et seulement si, pour cette direction, la contrainte tangentielle est nulle. On a, dans ce cas, ¹ = 靖¹n ¹, ² = 靖²n ² et ³ = 靖³n ³. Si 靖¹, 靖² et 靖³ sont tous différents de zéro et ont des valeurs distinctes, on dit que l’état de contrainte en O est triple : la quadrique des contraintes en O est alors une quadrique de centre O dont les axes sont situés selon les directions principales. Si 靖² = 靖³, la quadrique est de révolution, les directions principales sont l’axe Ox ¹ et toute direction issue de O et normale à Ox ¹. Si enfin 靖¹ = 靖² = 靖³, l’ellipsoïde des contraintes est une sphère et, toute direction issue de O étant principale, toutes les contraintes sont normales.

D’une manière générale, la détermination des contraintes et des directions principales se fait, dans chaque cas particulier, en cherchant les valeurs propres et les vecteurs propres de la matrice ( 靖^ij ) du tenseur 暈.

Cercles de Mohr

Les quadriques de contraintes fournissent déjà une représentation géométrique complète du tenseur des contraintes. Les cercles de Mohr en donnent une image incomplète mais souvent très maniable; ils répondent au problème suivant: si l’on se donne arbitrairement les valeurs de Tⁿ et de T^t (T^t 礪 O), existe-t-il une direction ょ telle que ces valeurs soient respectivement celles de la contrainte normale et du module de la contrainte tangentielle pour cette direction?

Si l’on repère l’espace à l’aide d’un repère principal Ox ⁱ , alors Tⁿ = 靖ⁱ n ^{i 2}, T^{t 2} + T^{n 2} = ( 靖ⁱ n ⁱ )² et n ⁱ n ⁱ = 1. Ces trois équations n’ont de solution en n ⁱ que dans la zone grisée du demi-plan (Tⁿ , T^t 礪 0) limité par les trois demi-cercles de la figure 4, appelés cercles de Mohr , admettant l’axe des Tⁿ pour diamètre et deux à deux tangents (chaque cercle correspond à un plan perpendiculaire à l’un des trois vecteurs propres).

Ainsi, si 靖¹ = 靖² = 靖³ = s , le problème n’admet de solution que si Tⁿ = s , T^t = 0 et, alors ょ est arbitraire. Ces cercles permettent de déterminer la valeur maximale de la contrainte tangentielle (ou du cisaillement) en un point quelconque; en effet, la figure montre que

dans le cas où 靖³ 麗 靖² 麗 靖¹, pour Tⁿ = ( 靖¹ + 靖³)/2 et ces valeurs sont obtenues pour n ¹² = n ³² = 1/2 et n ²² = 0, c’est-à-dire pour les directions des bissectrices de l’angle (Ox ¹, Ox ³) formé par les deux directions principales correspondant aux valeurs propres extrêmes.

Champ plan de contraintes

Un champ de contraintes est dit plan si les contraintes sont toutes parallèles à un plan fixe. Si (Ox ¹x ²) est choisi dans ce plan, les contraintes ne dépendent pas de Ox ³. Dans ce cas, le tenseur des contraintes est tel que 靖¹³ = 靖²³ = 靖³³ = 0 et sa matrice écrite en (7) est à deux lignes et deux colonnes. Les quadriques des contraintes sont alors des cylindres de génératrices parallèles à l’axe des x ³ et l’axe x ³ est un vecteur propre du tenseur (correspondant à la valeur propre nulle).

Sur les faces d’un petit cube d’arêtes parallèles aux axes, les contraintes se répartissent comme il est indiqué sur la figure 5.

2. Tenseur des déformations

Déformation d’un solide élastique

Un solide (S) subissant une déformation se transforme en un solide (S ) et un vecteur infiniment petit ABdu solide (S) se retrouve en A Baprès la transformation (fig. 6). La quantité scalaire 﨎 = (A B 漣 AB)/AB est la dilatation ou extension unitaire du segment AB; si 﨎 est positif, on dit qu’il y a eu traction de AB; s’il est négatif, il y a eu compression. Si les fonctions u ⁱ (i = 1, 2, 3) sont les composantes du déplacement AAdu point A de coordonnées x ⁱ , et si l’on appelle Xⁱ les coordonnées de A , on a Xⁱ 漣 x ⁱ = u ⁱ (x ¹, x ², x ³). Les déplacements correspondants Uⁱ du point voisin B (composantes de BB 轢) sont représentées par les trois équations Uⁱ = u ⁱ + u ^{i ,j} dx ^j et, après déformation, les composantes de A Bsont dx ⁱ + u ^{i ,j} dx^j . Le tenseur du second ordre faisant passer de ABà A B 轢, abstraction faite du déplacement AA 轢, est appelé tenseur des déformations en A et est noté 阮. Dans le repère (Ox ¹x ²x ³), ce tenseur est défini par ses neuf composantes u ^{i ,j} qui sont les éléments de la matrice (u ^{i ,j} ) écrite en (8) du tableau 2, les indices i et j désignant respectivement les numéros des lignes et des colonnes. Pour faire apparaître la déformation abstraction faite de la translation AA 轢, il suffit de mener A ¹B ¹équipollent à A Bpar le point A. Sur ABet A ¹B ¹ 轢, portons respectivement les points ¹ et ² tels que A¹ = A² = 1. Le vecteur ¹²est appelé vecteur déplacement angulaire ou plus simplement déplacement angulaire (fig. 7). Il a même mesure que l’angle (AN¹A²) exprimé en radians.

Considérons la facette (P) et un plan (Q) parallèle à (P) et infiniment voisin de (P); soit R l’intersection avec Q de la normale à la facette en A (fig. 8).

Au cours de la déformation, ce plan (Q) glisse par rapport au plan (P), de sorte que la ligne de points matériels AR cesse d’être normale à la facette. Soit alors A nla normale à la facette déformée (P ); le glissement de (Q) par rapport à (P) est mesuré par l’angle infiniment petit 塚 de A net A R 轢. Mais l’angle 塚 ne précise pas la direction dans laquelle s’est produit le glissement de (Q) par rapport à (P). Il suffit alors de porter sur A net A Rles points n ² et n ¹ tels que A n ² = A n ¹ = 1. Le vecteur n ²n ¹a même mesure que l’angle 塚 exprimé en radians et pour direction celle du glissement de (Q) par rapport à (P). Ce vecteur n ²n ¹est, par définition, le glissement de la facette considérée (fig. 9). Il faut remarquer qu’il n’est pas modifié par un déplacement d’ensemble. Comme la dilatation et contrairement au déplacement angulaire, le glissement a toujours la même valeur, que la déformation soit pure ou non.

Déformation pure et rotation pure

Le tenseur 阮 peut se mettre facilement sous la forme d’une somme de deux tenseurs 杻 et 倫, les matrices correspondantes étant respectivement ( 﨎^ij ) et ( 諸^ij ),

Le tenseur 杻 correspond à une déformation pure sans rotation, et le tenseur 倫 à une rotation pure sans déformation, comme cela se produit dans le cas particulier d’un corps solide indéformable (fig. 10). Le tenseur 杻 est symétrique, 倫 est antisymétrique. Mais, si on considère seulement les déformations continues infiniment petites (d’un grand intérêt pratique), on arrive, en négligeant les infiniment petits du second ordre dans les expressions des 﨎^ij et 諸^ij , à:

expressions qui sont explicitées en (9) et (10).

Dans certains ouvrages, les termes 﨎²³ = 﨎³², 﨎¹³ = 﨎³¹, 﨎¹² = 﨎²¹ sont quelquefois notés g ¹, g ², g ³ ou encore 塚¹/2, 塚²/2, 塚³/2 où les 塚ⁱ sont les glissements définis plus haut. De même 諸²³ = 漣 諸³², 諸¹³ = 漣 諸³¹ et 諸¹² = 漣 諸²¹ sont notés p , q et r par analogie avec les notations classiques des composantes de la rotation instantanée d’un corps solide.

Les six paramètres 﨎^ij caractérisent la déformation pure ou intrinsèque , c’est-à-dire considérée en elle-même, abstraction faite du déplacement (ou translation) AAet de la rotation. Cette déformation intrinsèque est caractérisée par les variations des distances mutuelles des points de l’élément de volume considéré du corps, autrement dit par les dilatations des divers segments infiniment petits de l’élément de volume. Si ces six paramètres sont tous nuls en un point, il n’y a pas de déformation pure dans la petite portion de volume entourant ce point et réciproquement.

La somme = 﨎¹¹ + 﨎²² + 﨎³³ est un invariant, quel que soit le système d’axes considéré, et elle est appelée dilatation cubique unitaire (par unité de volume) due à la déformation en un point. Cette invariance est une propriété mathématique classique; la trace de la matrice ( 﨎^ij ) ne dépend pas de la base.

Étude du tenseur size=5size=5杻 size=5參 en un point

En menant, comme on l’a fait pour le tenseur des contraintes, dans la direction de chaque élément linéaire du solide dont le vecteur unitaire est ゎ, un rayon vecteur AP= 福 ゎ, où 福 = r/ 連 﨎^u |, où 﨎^u = u ⁱ 﨎^ij u ^j , on trouve que l’ensemble des points réels P, lorsque ゎ tourne autour de A, est une surface d’équation 﨎^ij x ⁱ x ^j = size=1^梁 r ² explicitée en (11). Elle est appelée quadrique des déformations en A. Les axes de cette quadrique sont les axes principaux de déformation en A et les trois plans correspondants, les plans principaux de déformation en A. Dans ce système d’axes, la matrice associée à 杻 est diagonale; les déformations transversales 﨎^ij (i j ) sont nulles pour ces directions, et les allongements 﨎¹¹, 﨎²², 﨎³³, notés dans ce cas 﨎¹, 﨎², 﨎³, sont appelés allongements principaux en A. Les axes principaux de déformation demeurent perpendiculaires après déformation, et un parallélépipède, dont les faces sont parallèles aux plans principaux, reste, après déformation, un parallélépipède rectangle.

La connaissance de la quadrique des déformations permet de trouver géométriquement le module de l’allongement unitaire dans n’importe quelle direction.

Déformation homogène, déformation plane

La déformation est dite homogène si les fonctions u ⁱ et Uⁱ précédentes sont linéaires en x ^k . Tous les termes du tenseur 阮 sont alors des constantes. Quelle que soit la direction, la déformation est, dans ce cas, la même pour tous les points du corps déformé.

On dit que la déformation d’un corps est plane lorsqu’en tous les points de chaque perpendiculaire à un plan fixe (P) les déformations sont identiques et toutes parallèles à (P).

Conditions de compatibilité

Étant donné un solide déformé, les six paramètres 﨎^ij sont des fonctions continues des coordonnées x ^k des points du corps. Ces fonctions ne peuvent être entièrement arbitraires; il est, en effet, nécessaire que l’on puisse trouver des fonctions u ⁱ (indépendantes des translations et des rotations subies antérieurement par le corps), telles que les 﨎^ij satisfassent aux définitions (9). En dérivant deux fois ces égalités par rapport à x ¹, x ², x ³ et en éliminant u ¹, u ², u ³, on trouve six relations dites conditions nécessaires de compatibilité. Elles sont écrites en (12). On montre que ces six conditions sont également suffisantes pour les corps simplement connexes, alors que, pour les corps multiplement connexes, on doit ajouter des conditions exprimant qu’il n’y a pas déplacement relatif, au cours de la déformation, des deux lèvres d’une coupure quelconque rendant le corps simplement connexe.

Comme on vient de le voir, un élément quelconque d’un corps peut être amené à sa position, sa forme et son orientation finales par la séquence des trois opérations suivantes appliquées à l’élément avant déformation:

– l’élément est déplacé par translation jusqu’à ce qu’un de ses points (son centre de gravité par exemple) occupe la position finale;

– l’élément subit les déformations 﨎^ij et son orientation reste telle que les directions principales de déformation ne subissent aucune rotation (tenseur 杻);

– l’élément subit une rotation 諸^ij qui l’amène à son orientation finale (tenseur 倫); c’est la rotation des directions principales de déformation qui est indépendante du choix des axes Ox ¹, Ox ², Ox ³.

3. Relations entre les contraintes et les déformations

Forces internes et déformations

Les forces intérieures dans un solide sont des actions s’exerçant de proche en proche; autrement dit, une molécule du corps n’exerce d’actions que sur les molécules immédiatement voisines. Il en résulte que les déformations en un point d’un corps dépendent de l’état de contrainte en ce point et en ce point seulement; il existe donc a priori une relation entre le tenseur des contraintes en un point et le tenseur des déformations en ce même point; et cela en chaque point du solide.

Or, la translation et la rotation pure n’introduisent pas de contraintes dans le solide; il s’ensuit que le tenseur 倫 ne doit pas intervenir dans cette relation qui doit donc lier le tenseur des contraintes 暈 au tenseur de déformation pure 杻 seul.

Pour un corps élastique, il y a donc en un point une relation entre les 靖^ij et les 﨎^ij , c’est-à-dire que la connaissance des six premières entraîne celle des six autres, et réciproquement; il existe donc six relations de la forme 靖^ij = f ^ij ( 﨎^kl ) où f ^ij est la fonction particulière reliant 﨎^kl à 靖^ij . Les déformations étant par hypothèse infiniment petites, chacune de ces fonctions f ^ij peut être remplacée par son développement limité au premier ordre; on a ainsi un système de six relations de la forme:

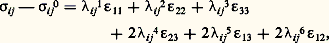
où les 靖^{ij 0} sont les contraintes à l’état initial, nulles si, dans cet état, le corps n’est pas sollicité et s’il est en régime de température uniforme. En résolvant ce système en 﨎^ij , on montrerait de même que les déformations sont des fonctions linéaires des contraintes. Les trente-six coefficients^{ij k} précédents qui relient les déformations aux contraintes sont les coefficients d’élasticité. Ils se réduisent en fait à vingt et un, car on démontre que^ij =^ji . La proportionnalité en un point entre la déformation intrinsèque et les contraintes constitue le principe de linéarité interne. Contrairement au principe de linéarité externe qui est fréquemment en défaut (voir ci-dessous), le principe de linéarité interne est toujours valable pour les matériaux de construction utilisés dans leur domaine élastique, car ces matériaux, du fait de leur rigidité, ne peuvent subir dans ce domaine que de très petites déformations intrinsèques.

Cas des corps homogènes et isotropes

Il est aisé de voir que, dans ces cas, les vingt et un coefficients d’élasticité se réduisent à deux. En effet, soit E et E les quadriques des contraintes et des déformations en un point d’un corps homogène et isotrope. Un plan principal de E constitue un plan de symétrie pour les contraintes; l’isotropie du corps exige alors que ce plan soit également plan de symétrie pour la déformation. Tout plan principal de E est donc aussi plan principal de E . Il en résulte que, en chaque point d’un corps homogène et isotrope, la quadrique des contraintes et celle des déformations ont mêmes directions principales. En prenant ces directions principales comme axes de coordonnées, les dilatations et contraintes principales 﨎¹, 﨎², 﨎³ et 靖¹, 靖², 靖³ restent donc seules différentes de zéro. Les équations précédentes reliant les contraintes et les déformations se réduisent aux trois relations 靖ⁱ =^ij 﨎^j explicitées en (13) du tableau 3 et où, pour simplifier, les contraintes initiales sont supposées nulles.

Du fait de l’isotropie, on a: ^ij =^ji d’où 靖ⁱ = 見﨎ⁱ + 廓 ( 﨎^j + 﨎^k ) avec i , j , ou k = 1, 2, 3 et i , j , k tous différents; ces trois relations, explicitées en (14), ne contiennent plus que deux coefficients d’élasticité 見 et 廓. Elles peuvent encore se mettre sous la forme 靖ⁱ = + 2 猪 﨎ⁱ développée en (15) avec = 廓 et 猪 = 見 漣 廓. Les deux coefficients et 猪 sont les coefficients d’élasticité de Lamé.

Proportionnalité du glissement et du cisaillement

Les quantités 﨎¹¹, 﨎²², 﨎³³ sont les dilatations dans la direction des axes de coordonnées. Le point P situé sur Ox et tel que OP = 1 vient, dans la déformation pure, en P¹, de coordonnées (1 + 﨎¹¹, 﨎¹², 﨎¹³). Les projections sur Oz et Oy du déplacement angulaire de P sont donc 﨎¹³ et 﨎¹² et celles du glissement de la facette perpendiculaire à Ox sont 2 﨎¹³ et 2 﨎¹². L’interprétation est analogue pour les deux autres facettes principales. Les 﨎²³, 﨎¹³, 﨎¹² sont donc les demi-composantes du glissement des plans principaux, ces demi-composantes se combinant comme sur la figure 11. Par définition, les directions principales n’ont pas de déplacement angulaire dans la déformation pure; si donc on prend ces directions comme axes de coordonnées, on a: 﨎²³ = 﨎¹³ = 﨎¹² = 0 et l’on peut poser 﨎¹¹ = 﨎¹, 﨎²² = 﨎², 﨎³³ = 﨎³.

La représentation de Mohr relative aux contraintes montre que, pour une facette d’orientation donnée par rapport aux contraintes principales, le cisaillement est fonction des différences des contraintes principales. La construction du demi-glissement est analogue et ce demi-glissement est fonction des demi-différences des dilatations principales. Or les différences des dilatations principales sont proportionnelles aux différences des contraintes principales, puisque les relations (15) donnent:

Le glissement est donc aussi proportionnel au cisaillement et on a 靖^ij = 2 猪 﨎^ij (i j ), expressions explicitées en (16).

Le coefficient 猪 de Lamé est souvent désigné par G que l’on appelle module de Coulomb , de torsion ou de glissement. Les relations (16) s’expriment aussi en fonction du glissement 塚: 靖^ij = 猪 塚^ij .

Relations générales entre les contraintes et les déformations

Dans le cas général, les axes de coordonnées n’étant pas les axes principaux, pour les corps homogènes et isotropes, on peut écrire simultanément les équations (15) et (16), en remplaçant dans (15) 靖ⁱ par 靖ⁱⁱ et 﨎ⁱ par 﨎ⁱⁱ . Inversement, ces équations peuvent être résolues en 﨎ⁱⁱ et 﨎^ij (i j ) pour obtenir les déformations en fonction des contraintes.

On pose:

ou inversement

Le nombre E est appelé module d’Young ou module élastique du matériau constituant le corps considéré. C’est une caractéristique intrinsèque de ce matériau et il a, comme une contrainte, les dimensions d’une pression. Le nombre 益 est appelé coefficient de Poisson du matériau dont il est également une caractéristique intrinsèque; il est sans dimension.

Compte tenu de ces deux nouvelles quantités, les équations (15) et (16) s’écrivent alors sous la forme générale (17) et (18).

Les coefficients E et 益 ne constituent pas deux nouveaux coefficients d’élasticité puisqu’ils ne sont pas indépendants des coefficients de Lamé et 猪. En effet, il ne peut y avoir, pour une substance homogène et isotrope donnée, que deux coefficients d’élasticité indépendants.

Signification physique du module de Young et du coefficient de Poisson

Sur une tige cylindrique de section droite S, on marque deux traits distants de l ⁰ sur une même génératrice (fig. 12). Aux deux extrémités de la tige, on applique suivant son axe une force F^x au moyen d’une machine de traction. La tige s’allonge et la distance des deux traits devient

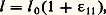
où 﨎¹¹ est la dilatation linéaire suivant Ox .

L’état de contrainte dans cette barre, à une distance suffisante des extrémités, est un état de contrainte simple d’axe Ox ¹. La contrainte principale non nulle, 靖¹¹, est dirigée selon l’axe Ox et a pour valeur F^x /S. En d’autres termes, l’état de contrainte est:

La région centrale de la barre est en état de traction simple. Les dilatations principales sont alors, en vertu des formules qui précèdent,

Ces relations montrent que la force F^X provoque dans la barre:

– un allongement selon Ox ¹, caractérisé par la dilatation 﨎¹;

– une contraction transversale selon un axe quelconque perpendiculaire à Ox ¹, caractérisée par la dilatation 﨎².

On voit aussi que le module d’Young est égal au rapport de la contrainte principale à la dilatation correspondante dans un état de traction simple. C’est également la contrainte qu’il faudrait appliquer à la tige, si le domaine élastique n’était pas limité, pour que son allongement devienne égal à sa longueur initiale – autrement dit, pour doubler la longueur de la barre.

Le coefficient de Poisson est égal au rapport de la contraction transversale et de la dilatation longitudinale.

La dilatation cubique est:

Elle est positive dans l’expérience de traction (sauf pour le caoutchouc) et s’accompagne d’une augmentation de volume.

Il est facile de déterminer expérimentalement les coefficients E et 益. Si l’on augmente lentement et progressivement F^x jusqu’à ¹ dans l’expérience précédente, 靖¹ et 﨎¹, ainsi que 﨎² égal à 﨎³, varient. En portant 﨎¹ en abscisse et 靖¹ en ordonnée, on obtient une courbe OA appelée courbe de charge ou courbe de traction (fig. 13). Puis, en diminuant lentement F^x jusqu’à zéro, 﨎¹ diminue et les nouveaux couples ( 靖¹, 﨎¹) se placent exactement sur la même droite OA que celle suivie pendant l’accroissement de F, ce qui caractérise l’élasticité de la matière: lorsque F^x reprend la valeur zéro, la longueur de la tige est égale exactement à sa longueur initiale l ⁰ et 﨎¹ est nulle. Le domaine élastique est représenté par la droite OL et s’étend jusqu’à L qui correspond à une valeur 靖^e de la contrainte appelée limite élastique. Dans cette zone, la déformation est réversible et il existe une relation linéaire entre la contrainte et la déformation qui constitue la loi de Hooke . Au-delà de la limite élastique L, la courbe de décharge A B ne coïncide plus avec la courbe de charge OA et il reste une déformation permanente OB lorsque la force F^x disparaît. La zone LA est appelée zone de plasticité . Si F^x croît encore au-delà de A , la tige se rompt pour une certaine valeur; des matériaux fragiles (fonte, verre) se rompent en traction sans avoir reçu de déformation permanente appréciable.

La valeur usuelle de 益 pour la plupart des métaux est comprise entre 0,25 et 0,30; elle est de 0,5 pour le caoutchouc. Le coefficient de Poisson est toujours positif; il n’existe pas aujourd’hui de matériaux pour lesquels 益 serait négatif (augmentation de section en traction). Si 益 = 0,30, on déduit G = (5/13) E; par exemple, pour l’acier, E = 2 練 10¹¹ pascals et G 力 8 練 10¹⁰ pascals.

Critères de limite élastique

Dans l’expérience précédente de traction, les deux contraintes 靖² et 靖³ sont nulles. Dans ces conditions, on définit une limite élastique 靖^e à ne pas dépasser pour 靖¹ afin que le matériau ne subisse pas de déformation permanente. Il est utile de savoir quelle est la limite élastique lorsque les trois contraintes principales sont différentes de zéro.

On peut admettre que, dans le cas d’un matériau homogène et isotrope, la limite élastique ne dépend que de la grandeur des contraintes principales et non pas de leurs directions. Le critère généralement utilisé est celui de Tresca, d’après lequel la limite élastique est atteinte lorsque le rayon du plus grand des trois cercles de Mohr atteint la valeur 精^E (c’est la composante tangentielle maximale 精^e de la contrainte qui produit la déformation permanente par glissement des particules matérielles). Si 靖¹ et 靖² sont les deux contraintes principales extrêmes et 靖³ la contrainte moyenne, le critère de Tresca s’écrit:

Un autre critère faisant intervenir 靖³ a été proposé par von Misès:

Pour les matériaux plastiques, ces deux critères donnent d’assez bons résultats. Mais pour les autres matériaux, ils s’éloignent de la réalité. Caquot a perfectionné le critère de Tresca par la théorie de la courbe intrinsèque; pour chaque matériau, il existe une fonction f ( 靖¹ + 靖²) telle que la limite élastique soit définie par:

en supposant toujours que 靖¹ et 靖² sont les contraintes extrêmes. La fonction f ( 靖¹ + 靖²) est à déterminer expérimentalement. On a également proposé un critère encore plus général:

réunissant les avantages que présentent séparément tous les critères précédents. La fonction g qui doit encore être déterminée expérimentalement a l’allure indiquée par la figure 14.

4. Déformations élastiques linéaires

Principe de superposition. État naturel

En restant dans le domaine linéaire élastique, on peut utiliser le principe de superposition: si, à deux états de contraintes, correspondent deux états de déformations, la superposition des contraintes correspondra à celle des déformations. Cela suppose naturellement qu’à une déformation nulle correspondent des efforts intérieurs nuls, c’est-à-dire que le solide soit dans l’état naturel. En réalité, cela n’est jamais réalisé exactement. La trempe des métaux laisse subsister des contraintes intérieures importantes en l’absence de toute force extérieure. C’est pour les diminuer qu’on procède au recuit. De même, en l’absence de force extérieure, le fait de porter un solide à une température non uniforme crée à l’intérieur de celui-ci des contraintes thermiques. Le principe de superposition ne s’applique qu’aux variations des contraintes , à partir de l’état initial qui n’est pas toujours un état naturel. La théorie de l’élasticité ne permet de calculer que les variations de ces contraintes.

Principe de linéarité externe

Appliquons à un corps un chargement (F) composé d’un certain nombre de forces づ¹, づ², ..., づⁿ et soit u , v, w les composantes du déplacement d’un point M du corps. Soit (F) le chargement obtenu en multipliant toutes les forces par un nombre; la direction des forces reste inchangée. On dit qu’il y a linéarité externe si u , v et w sont proportionnels à la grandeur du chargement. Ce principe doit être distingué du principe de linéarité interne qui suppose la proportionnalité des six paramètres de déformation locaux 﨎^ij aux chargements et aux contraintes 靖^ij .

Puisque les déformations sont élastiques, u , v et w sont, par définition, des fonctions bien définies de. On montre que les petites déformations d’un solide élastique obéissent en général au principe de linéarité externe. Cependant, ce principe peut être mis en défaut même pour des corps très rigides pour lesquels les déplacements u , v et w ont des valeurs notables; c’est le cas d’une poutre en acier très élancée pour laquelle les déplacements u , v et w peuvent être grands, même si, localement, le principe de linéarité interne est respecté.

Théorème de Clapeyron et théorème de réciprocité

Le théorème de Clapeyron, valable sous réserve qu’il y ait linéarité externe, s’énonce de la façon suivante: Le travail (ou énergie de déformation) dépensé pour faire passer un système d’un état initial S⁰ non sollicité à un nouvel état S d’équilibre sous l’action d’un chargement (F) est égal à la moitié du travail des forces extérieures produisant la déformation totale.

Le théorème de réciprocité, valable sous la même réserve, s’énonce: Si deux systèmes de forces (F¹) et (F²), appliqués séparément à un ensemble de solides, lui impriment des systèmes de déplacement élastiques respectifs ( ¹) et ( ²), le travail de (F¹) sur ( ²) est égal à celui de (F²) sur ( ¹).

Dans le cas général d’axes Ox ¹, Ox ², Ox ³ quelconques, cette énergie de déformation s’écrit:

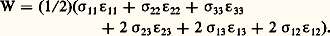
5. Le problème général de l’élasticité

Détermination des déplacements, des déformations et des contraintes

Un corps élastique résiste en se déformant aux actions de surface auxquelles il est soumis, et des contraintes apparaissent dans ce corps; les actions de surface étant données, quelles sont, pour tous les points du corps, les déformations, les déplacements et les contraintes?

Si le champ des déplacements u ⁱ (x ^k ) a été déterminé, les déformations et les contraintes s’en déduisent immédiatement par les formules du tableau 3. Inversement, si les déformations ou les contraintes ont été déterminées, on pourra en déduire les déplacements par les formules (19) et (20) du tableau 4 obtenues en intégrant les équations (9) et en passant par l’intermédiaire des relations (10) du tableau 2. Dans ces relations, les indices zéro sont relatifs à un point origine O quelconque, et les intégrales sont étendues à une ligne quelconque joignant O à M. Ces déplacements ne sont définis qu’à une rotation et une translation près.

Équations aux déplacements

Supposons les déplacements infiniment petits. En chaque point intérieur du corps, il est nécessaire que les fonctions u ¹, u ², u ³ soient telles que les contraintes qui y apparaissent satisfassent aux trois équations d’équilibre (5), et cette condition est suffisante. On obtiendra donc les équations générales portants sur u ¹, u ², u ³ en remplaçant, dans les équations d’équilibre, les valeurs 靖^ij en fonction des u ^k , c’est-à-dire les valeurs (15) et (16), compte tenu des relations (9). On est conduit alors aux trois équations (21) où

est le laplacien, et où les X^1m sont les composantes cartésiennes des forces de volume. L’intégration de ces équations introduit des fonctions arbitraires déterminées par les conditions à la surface qui s’écrivent facilement à partir des égalités (4) du tableau 1.

Équations aux déformations et équations aux contraintes

Les équations devant être satisfaites en tous les points du corps seront au nombre de neuf: les six équations de compatibilité (12) et les trois équations obtenues en remplaçant les 靖^ij par leurs valeurs en fonction des 﨎¹¹, 﨎²², 﨎³³ dans les trois équations de l’équilibre (5). Les trois conditions de surface s’obtiennent immédiatement à partir des équations (4). Ces douze égalités sont nécessaires et suffisantes pour les corps simplement connexes. Pour les corps multiplement connexes il y a lieu d’ajouter les conditions spéciales dont il a été question précédemment.

Les équations aux contraintes sont au nombre de neuf: les trois équations d’équilibre (5) et les six équations obtenues en remplaçant dans les équations de compatibilité (12) les 﨎¹¹, 﨎²², 﨎³³ par leurs valeurs en fonction des 靖^ij . On obtient les équations de Beltrami avec la même réserve que ci-dessus pour les corps multiplement connexes.

6. Cas des corps réels

Dans la théorie de l’élasticité, on admet, comme on l’a vu plus haut, que les actions réciproques des divers éléments de matière sont des actions de proche en proche. Dans un corps réel, quelle que soit la conception physique des actions mécaniques internes considérée, un élément de matière a certainement une action sur des éléments situés à une distance petite mais finie; on peut, cependant, admettre qu’au-delà d’une distance d ¹ qui est très petite, l’action mutuelle de deux particules est négligeable.

Longueur d’homogénéité

La matière réelle n’est en fait ni homogène, ni isotrope; un morceau d’acier, par exemple, est constitué par un agrégat complexe de cristaux d’espèces différentes enchevêtrés entre eux. Les seules propriétés qui soient les mêmes en tous les points et dans toutes les directions sont celles qui sont relatives à une quantité finie de matière composée d’un très grand nombre de cristaux considérés globalement. On ne peut donc imaginer la matière réelle comme homogène et isotrope que si on ne l’examine pas à une trop petite échelle.

Considérons des petits cubes de matière de côtés l ; il existe une longueur l ¹ au-dessous de laquelle ces petits cubes ne peuvent être considérés comme ayant les mêmes propriétés et cela à cause de l’hétérogénéité microscopique de la matière. La longueur l ¹ est la longueur d’homogénéité. Pour l’acier, l ¹ peut être de l’ordre du dixième de millimètre; pour certains alliages, elle peut être beaucoup plus grande.

On peut considérer qu’on a toujours l ¹ 礪 d ¹. Il résulte de ces considérations qu’une théorie supposant les corps homogènes et isotropes ne sera entièrement applicable aux corps réels que si les longueurs qui interviennent dans cette théorie sont supérieures à l ¹ et à d ¹. Tel n’est pas le cas de la théorie de l’élasticité qui fait intervenir des longueurs infiniment petites. Examinons les difficultés qui peuvent en résulter pour la définition de la contrainte.

Contraintes

Soit un élément d 行 de la surface ( ) d’un corps donné et soit れ la somme des forces internes appliquées à d 行. Portons en abscisse d 行 et en ordonnée s /d 行 et faisons tendre d 行 vers zéro. Le rapport s /d 行 est bien défini et varie de manière continue tant que d 行 礪 d 行¹, d 行¹ étant une surface dont les dimensions sont du même ordre de grandeur que la longueur d’homogénéité. Lorsque d 行 麗 d 行¹, s /d 行 a des valeurs incohérentes. Deux cas peuvent alors se produire:

1. Le rapport s /d 行 atteint pratiquement une valeur limite et れ une direction limite avant que d 行 ait atteint la valeur d 行¹; on appelle alors contrainte le vecteur ayant pour grandeur et direction ces valeurs limites. Bien que ce soit physiquement incorrect, on peut dire, d’une manière abrégée, que la contrainte est la limite du rapport s /d 行 lorsque d 行 tend vers zéro (fig. 15 a).

2. Le rapport s /d 行 n’a pas encore atteint de valeur limite lorsque d 行 = d 行¹ (fig. 15 b); on ne peut alors définir la contrainte, et la théorie classique tombe en défaut. Ce cas se produit:

– lorsque les cristaux ne sont pas très petits par rapport aux dimensions de la pièce;

– dans les régions où les efforts internes varient rapidement d’un point à un autre, ce qui se produit aux environs des régions de la surface extérieure ayant une très forte courbure ainsi qu’au voisinage des points de la surface extérieure où sont appliqués des efforts concentrés, par exemple dans les régions où deux pièces, dont l’une a une forte courbure, entrent en contact ponctuel. Certaines anomalies dans les lois de la rupture des pièces peuvent d’ailleurs résulter de cette impossibilité de définir la contrainte.

7. Photoélasticité

Lorsque la forme de la pièce à étudier est trop compliquée pour que les calculs théoriques soient abordables, on utilise des méthodes de calcul numérique (calculs aux différences finies) ou des méthodes expérimentales telles que la mesure des déformations par jauges de contraintes ou encore la méthode photoélasticimétrique. Elle consiste à examiner les pièces soumises à des efforts mécaniques à l’aide d’une lumière polarisée qui fait apparaître des franges brillamment colorées, variables suivant la grandeur des efforts auxquels la pièce est soumise et que l’on étalonne en appliquant par exemple à l’éprouvette des efforts simples (cf. LUMIÈRE – Diffraction). On détermine ainsi également la différence des contraintes principales et leurs directions à l’aide de polaroscopes simples et leurs grandeurs à l’aide d’appareils plus compliqués. La photoélasticimétrie est aussi possible à trois dimensions; dans ce cas, on utilise souvent des résines spéciales enduites à chaud sur les pièces à étudier et qu’on laisse refroidir sous charge. Celles-ci sont ensuite découpées puis examinées au polaroscope, et on en déduit les contraintes. La méthode photoélasticimétrique a permis d’aboutir à des résultats particulièrement importants dans l’étude des zones de concentration de contraintes au voisinage des ouvertures ou des angles rentrants des pièces; dans ces zones, en effet, les contraintes sont particulièrement élevées.

• 1687; lat. sc. elasticitas → élastique

1 ♦ Propriété qu'ont certains corps de reprendre (au moins partiellement) leur forme et leur volume primitifs quand la force qui s'exerçait sur eux cesse d'agir. L'élasticité du caoutchouc. Élasticité des gaz. ⇒ compressibilité; détente, expansion. Élasticité des métaux (de traction, de torsion, de flexion). ⇒ extensibilité, flexibilité. Limite d'élasticité, au-delà de laquelle les corps restent déformés. Coefficient d'élasticité. Module d'élasticité : constante qui relie la déformation à la contrainte subie par le corps élastique. Constante d'élasticité : inverse du module. — Physiol. Élasticité des artères, des muscles, des poumons.