DYNAMIQUE
La dynamique introduit la notion d’effort s’exerçant sur un ensemble mécanique. Son but est de relier les efforts aux mouvements possibles de cet ensemble (en permettant de calculer les efforts, si l’on connaît le mouvement, ou, inversement, de déterminer le mouvement, si les efforts sont donnés ou peuvent être éliminés pour ceux d’entre eux qui seraient inconnus a priori).
La notion d’effort est issue de l’expérience quotidienne: les contacts de l’homme avec son environnement. Au fur et à mesure du développement scientifique des conceptions mécaniques, on est arrivé à unifier la notion d’effort de contact et la notion d’action à distance en les regroupant dans un même concept.
Ces notions, relativement vagues, doivent être précisées à l’aide de principes qui, dans l’état actuel de la science classique, résument et idéalisent les propriétés générales que nous attribuons à la notion d’effort d’interaction entre ensembles matériels: association d’un torseur à des efforts exercés par un ensemble matériel sur un autre ensemble matériel, principe de réception (le torseur d’action sur une réunion est la somme des torseurs d’action sur chacun des éléments), principe de génération (le torseur d’action d’une réunion sur un ensemble est la somme des torseurs d’action de chacun des éléments sur cet ensemble). Parmi tous les efforts s’exerçant sur un ensemble matériel déterminé, le mécanicien est amené à établir une distinction entre les «efforts extérieurs» à l’ensemble matériel considéré (efforts exercés par le reste de l’Univers sur cet ensemble) et les «efforts intérieurs» (efforts exercés par les éléments de l’ensemble les uns sur les autres).
Le principe fondamental, sous sa forme la plus usuelle, s’applique justement à un ensemble matériel bien déterminé et ne fait intervenir que les efforts extérieurs: il s’exprime par l’égalité entre le torseur des efforts extérieurs et le torseur dynamique (qui a été défini en cinétique), il postule l’existence d’au moins un repère et d’au moins une manière de mesurer le temps pour lesquels cette égalité est vraie. Un tel repère privilégié est dit galiléen. De cette égalité entre torseurs, on déduit, d’abord, deux égalités entre éléments de réduction de chacun des torseurs (somme et moment), puis on déduit de ces deux égalités vectorielles six équations scalaires. Au cours du développement historique de la mécanique, c’est le processus inverse qui a eu lieu: équations scalaires, équations vectorielles, égalité entre torseurs, les progrès mathématiques permettant à chaque fois des exposés synthétiques plus concis.
L’application du principe fondamental permet également de traiter le cas particulier de l’équilibre et de démontrer le théorème de l’action et de la réaction.
Le champ d’application du principe fondamental est absolument général. Ce principe fournit, pour chaque ensemble mécanique choisi par le calculateur, six équations différentielles du second ordre faisant intervenir, d’une part, les composantes d’éléments de réduction de torseurs inconnus (introduits notamment par les actions de contact) et, d’autre part, la variable de temps ainsi que les variables de configuration (permettant de situer l’ensemble dans le galiléen) et leurs dérivées premières et secondes par rapport au temps. Bien entendu, en dynamique, on cherche, comme en mathématiques, à abaisser l’ordre des équations différentielles obtenues, et on le fait d’autant plus volontiers que les équations de la mécanique sont toujours assez complexes: c’est pourquoi on détecte systématiquement les intégrales premières.
Du principe fondamental on peut encore déduire de manière très générale les équations scalaires, dites équations de la dynamique analytique, lesquelles sont formées quasi automatiquement à partir d’opérations différentielles appliquées à l’énergie cinétique de l’ensemble mécanique et à la puissance développée par tous les efforts agissant sur lui.
Cette autre manière de traiter la mécanique, complètement équivalente à celle qui est issue du principe fondamental, est généralement considérée comme moins concrète. Pour en simplifier l’exposé, nous limiterons son champ d’application aux solides et à un ensemble fini de solides, pour lesquels nous écrirons en particulier les équations de Lagrange. Cette mécanique analytique conduit également à des intégrales premières (spécialement intégrale première de l’énergie et intégrale première de Painlevé).
Quelle que soit la manière dont on se propose d’aborder l’étude du mouvement d’un ensemble mécanique, il faut se rappeler qu’en dynamique il existe une classe de repères privilégiés auxquels on doit rapporter le mouvement. Or, en mécanique terrestre, qui est la plus fondamentale, dans l’état actuel de nos possibilités et de nos besoins, le repère qui se présente le plus naturellement est un repère lié à la Terre. Mais, bien qu’il ne fasse pas partie des repères privilégiés, il s’est comporté comme tel dans l’évolution des recherches en mécanique jusqu’à l’apparition technologique de solides tournant à grande vitesse et de déplacements rapides suivis pendant longtemps et avec précision.
L’étude des corrections systématiques à effectuer dans toutes les questions où la Terre ne peut pas être considérée comme un galiléen pose le problème plus général de l’étude des mouvements rapportés à des repères quelconques (cette rubrique est généralement appelée étude des mouvements et des équilibres relatifs). Moyennant l’intervention de deux systèmes de forces complémentaires, les équilibres et mouvements relatifs peuvent être traités comme des équilibres et des mouvements galiléens, et l’on retrouve à ce propos les deux aspects équivalents de la mécanique.
Puisque le principe fondamental fait intervenir les efforts extérieurs agissant sur un ensemble matériel, la mécanique emprunte à la pratique expérimentale des lois sur les champs de force dont quelques exemples simples sont exposés ici (frottements, gravitation, contacts élastiques). On a supposé jusqu’ici que les paramètres de configuration avaient des dérivées premières continues par rapport à la variable de temps; on examinera donc enfin les modifications à introduire dans les équations issues du principe fondamental, aux instants où cette continuité n’a plus lieu (phénomènes de chocs). On profite de cette étude pour exprimer un nouvel énoncé du principe fondamental dont la forme sera plus commode pour l’application à des ensembles mécaniques assez compliqués (fusées).
Dans les ouvrages de mécanique, on a l’habitude de traiter la dynamique après avoir exposé les théories partielles que sont la cinématique et la cinétique. Cet article comportera donc de nombreux renvois aux articles CINÉMATIQUE et CINÉTIQUE qui exposent ces concepts de base et contiennent les principaux résultats des calculs fondamentaux les concernant.
1. Efforts s’exerçant sur un ensemble mécanique
Efforts extérieurs à un ensemble matériel
L’expérience quotidienne montre que les ensembles matériels ont des actions les uns sur les autres: l’aimant attire le fer, un objet quelconque abandonné à lui-même est attiré vers la Terre, une marche d’escalier après un long usage présente une usure notable, la molette du briquet en frottant sur la pierre provoque une étincelle, etc. Dans les deux premiers exemples (aimant et chute des corps), les ensembles matériels qui interagissent ne sont pas en contact; on dit que les actions sont à distance. Au contraire, dans les deux derniers exemples, les interactions des deux ensembles matériels sont dues au fait que les molécules de l’un et de l’autre sont en contact; on a des actions dites de contact qui traduisent de manière idéale les faits expérimentaux.
On admet généralement les principes suivants:
Principe I. – Les efforts exercés par un ensemble matériel 1 sur un ensemble 2 disjoint de 1 (c’est-à-dire sans élément commun avec 1) forment un torseur que l’on note 12 (cf. CINÉMATIQUE, chap. 4).
Principe II. – Étant donné trois ensembles disjoints 1, 2, 3,
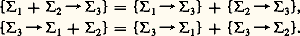
Le principe II s’étend de proche en proche à un nombre fini quelconque n d’ensembles disjoints.
On appelle alors torseur des efforts extérieurs agissant sur un ensemble matériel le torseur des actions exercées sur par tous les ensembles matériels de l’Univers, disjoints de et constituant l’ensemble complémentaire de noté . Ce torseur joue un rôle essentiel en dynamique; nous le noterons: face=F0019 .
Ce torseur fait en général intervenir des torseurs d’efforts relatifs à différentes lois physiques (attraction newtonienne, actions électriques, actions magnétiques, actions de contact...). Suivant le système considéré, certaines de ces lois donneront des torseurs prépondérants par rapport à d’autres. Par exemple, si est un électron, l’action électrique exercée par un autre électron est 4,17 . 1042 fois plus grande que l’action de gravitation.
L’ensemble des lois physiques et des éléments de dont on tient compte constitue un schéma d’étude dont l’adéquation doit être vérifiée, compte tenu de l’ordre de grandeur des termes négligés, par rapport à l’approximation recherchée. La deuxième partie du second principe permet d’effectuer une partition sur un ensemble , c’est-à-dire de le considérer comme la réunion de sous-ensembles disjoints; le torseur sera la somme des torseurs d’efforts exercés par sur chacun des sous-ensembles de la partition effectuée. On est donc ramené à définir le torseur des efforts exercés par sur un point M ou le voisinage d’un point M. On admettra que ces torseurs d’efforts extérieurs à un ensemble matériel sont définis, d’une part, par des densités de forces みi (M) et des densités de couples ぢ 見 (M) relatives à différentes mesures (fixées chaque fois par la loi physique considérée) et, d’autre part, par des torseurs d’efforts concentrés 淪j. Les éléments de réduction du torseur des efforts extérieurs à seront donc de la forme:

ce qui s’écrit sous forme condensée (notations évidentes):
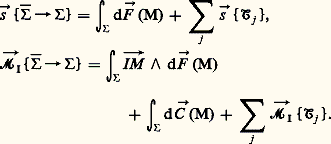
Un exemple courant de torseurs d’efforts concentrés est celui de deux solides rigides en contact ponctuel ou, plus exactement, dont le contact a lieu sur une surface de mesure négligeable. Comme exemple simple de densité de force définie par unité de mesure de surface, on peut citer les contraintes (M) conduisant à l’effort élémentaire (M)dS (M) agissant sur le voisinage de M. L’accélération む (M) due à la pesanteur constitue un exemple de densité de force définie par unité de mesure de masse: l’effort む(M)dm (M) agit, du fait de l’attraction terrestre, sur le voisinage de M.
Efforts intérieurs
On donne le nom d’effort intérieur à un ensemble matériel à tout effort s’exerçant entre deux sous-ensembles quelconques de . On ne définira pas ici les efforts intérieurs à un milieu continu, pour lesquels les principes admis pour les efforts extérieurs ne sont pas adéquats. Cependant, il faut bien noter que, si l’on effectue une partition d’un milieu continu, les interactions entre deux éléments de la partition, devenant des efforts extérieurs à chacun de ces éléments, se représentent (globalement) par un torseur.
La propriété pour un système d’efforts d’être intérieur ou extérieur n’est pas intrinsèque au système matériel considéré; les interactions entre deux ensembles 1 et 2 sont des efforts extérieurs à 1 et à 2 mais des efforts intérieurs à la réunion de 1 et 2.
2. Le principe fondamental
Énoncé
Il existe au moins un repère d’espace, dit absolu ou galiléen (g), et une échelle de temps , privilégiée par définition, tels que, pour tout ensemble matériel et à tout instant, le torseur dynamique 遼g size=1, défini dans l’article CINÉTIQUE, est égal au torseur des efforts extérieurs agissant sur :

Ce principe est à la base de toute étude mécanique. Son énoncé admet l’existence d’au moins un repère privilégié en dynamique, alors que tous les repères introduits en cinématique et en cinétique étaient équivalents. La validité de ce principe est vérifiée par l’expérience.
Ayant admis l’existence d’un repère absolu, la formule de composition des accélérations entraîne que tout repère en translation rectiligne et uniforme par rapport à ce repère absolu sera aussi galiléen. Il existe donc une classe des galiléens qui sont indiscernables les uns des autres par l’expérience.
Dans des schémas d’étude, certains repères non galiléens pourront être considérés comme galiléens, lorsque l’erreur commise sera acceptable.
Conséquences du principe fondamental
Théorèmes généraux
L’égalité de deux torseurs entraînant l’égalité de leurs éléments de réduction en tout point, on en déduit les théorèmes suivants:
1. Théorème de la somme dynamique .

ce qui, compte tenu des résultats de cinétique, s’écrit (en désignant par G le centre d’inertie de l’ensemble matériel et par m ( ) sa masse):

Pour tout ensemble matériel , la quantité d’accélération galiléenne du centre d’inertie supposé doué de la masse totale est égale à la somme géométrique du torseur des efforts extérieurs agissant sur l’ensemble matériel considéré.
2. Théorème du moment dynamique .
L’égalité des moments en un même point I s’écrit:

Ainsi, pour tout ensemble matériel , le moment dynamique galiléen en un point quelconque est égal au moment, en ce point, du torseur des efforts extérieurs agissant sur l’ensemble matériel considéré.
Si un ensemble matériel est en équilibre, son torseur dynamique est le torseur nul, d’où =0 ce qui s’énonce: Si un ensemble matériel est en équilibre par rapport à un galiléen, le torseur des efforts extérieurs agissant sur lui est le torseur nul. Le principe fondamental de la statique est un cas particulier du principe fondamental de la dynamique.
3. Théorème de l’action et de la réaction .
Considérant une partition d’un ensemble en deux sous-ensembles disjoints 1 et 2 et appliquant successivement le principe fondamental à , 1 et 2, on montre que:

Quels que soient les deux ensembles matériels disjoints 1 et 2, le torseur des actions exercées par 1 sur 2 est opposé au torseur des actions exercées par 2 sur 1.
Cas des systèmes de masse négligeable
Dans la schématisation de certains systèmes mécaniques, il apparaît légitime d’admettre que la masse de certaines parties du système est suffisamment petite par rapport aux masses des autres parties de ce système pour pouvoir être négligée. C’est par un abus de langage que l’on parle de système de masse nulle, un organe ne pouvant avoir une masse négligeable que par rapport aux autres masses du système mécanique étudié. Soit un tel organe; si on lui applique le principe fondamental, on a =0.
En particulier, si ne subit des actions que des deux ensembles 1 et 2 (ce qui revient à dire que est la réunion de 1 et de 2), on obtient, en tenant compte du théorème de l’action et de la réaction, ( 1) = 2, ce qu’on traduit en disant que les organes de masse négligeable transmettent intégralement les actions qu’ils reçoivent.
Exemple d’application: solide libre dans l’espace
Soit un solide S sans liaison (ou libre), soumis uniquement à une densité massique de force uniforme et constante む. Appliquons successivement le théorème de la somme dynamique et le théorème du moment dynamique au solide S, de masse m , de centre d’inertie G; il vient:

L’équation vectorielle (1) entraîne immédiatement que le centre d’inertie G admet pour trajectoire galiléenne une parabole ou une droite (chute des corps).
L’équation vectorielle (2) s’écrit encore, G étant centre d’inertie de S [cf. CINÉTIQUE],

(face="EU Arrow" ゜0 vecteur constant dans le galiléen) ou, en explicitant,

Si 0 = , alors gS = et le mouvement de S est un mouvement de translation par rapport au galiléen.
Si 0 , l’équation vectorielle précédente se décompose en trois équations scalaires, par projection sur les axes principaux centraux d’inertie (Gx , Gy , Gz ):
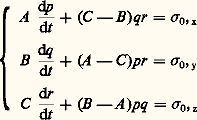
où A , B , C sont les moments centraux principaux d’inertie et p , q , r les composantes du vecteur 行gS sur les axes principaux centraux d’inertie [cf. CINÉTIQUE].
Les trois équations précédentes portent le nom d’équations d’Euler.
3. Dynamique analytique pour un ensemble de solides
Dans le cadre de la mécanique des systèmes formés d’un nombre fini de solides, les équations dites de la dynamique analytique se déduisent tout naturellement du principe fondamental de la dynamique. C’est ce formalisme que nous adopterons ici.
On remarque simplement que:
– quel que soit le torseur 慄, le principe fondamental de la dynamique entraîne pour tout ensemble matériel :
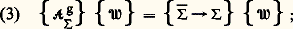
– quel que soit le torseur 慄, dans le cas où un torseur 杻 est défini sur un ensemble E par une densité vectorielle み (M) relative à une mesure 猪 , alors le produit scalaire des deux torseurs s’écrit:
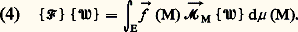
Théorème de l’énergie-puissance
Cas du solide unique S
Appliquons à un solide unique S l’égalité (3), en prenant comme torseur 慄 le torseur distributeurgS des vitesses de S par rapport au galiléen (g):
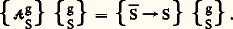
Le scalaireSSgS est, par définition, la puissance galiléenne développée par les efforts extérieurs à S. Si on applique au scalaire 遼 gS gS le résultat (4), il vient:

ce qui s’énonce: Pour un solide unique, la dérivée totale de l’énergie cinétique galiléenne est égale à la puissance galiléenne développée par les efforts extérieurs agissant sur S.
Dans le cas particulier (réalisé chaque fois que S n’est pas soumis à un champ électromagnétique) où le torseur des efforts extérieurs s’exerçant sur S est défini par des densités vectorielles みi (M) définies par rapport aux mesures 猪 i , si l’on pose, pour simplifier l’écriture,

le second membre s’écrit:

Dans le cas général, le second membre prend la forme:

où d ぢ(M) désigne la densité de couple:
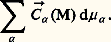
Cas d’un ensemble fini de solides
Pour chacun des solides Sj , le théorème précédent s’écrit:
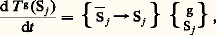
ou, en sommant sur j ,
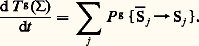
Pour un ensemble fini de solides, la dérivée par rapport au temps (dérivée totale) de l’énergie cinétique galiléenne du système est égale à la puissance galiléenne développée par tous les efforts extérieurs à chacun des solides constituant le système.
Remarquons que les efforts extérieurs à un solide déterminéSjSj se décomposent en efforts extérieurs à l’ensemble et en efforts s’exerçant entre les solides qui constituent (interefforts):
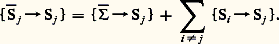
Il faut donc calculer la puissance développée par tous les efforts extérieurs à l’ensemble et par tous les efforts s’exerçant entre les Sj formant le système.
Équations de Lagrange pour un solide unique S
Appliquons à un solide unique S l’égalité (3) en choisissant comme torseur 慄 le torseur, qu’on noteragS,i, défini de la façon suivante:
gS,i a pour éléments de réduction en tout point M de S où il est défini:

où les q i désignent les paramètres repérant, par rapport à (g), la position de S (n 諒 6). La relation (1) s’écrit ici:

Calculons le premier membre en appliquant (4):

g (M) est évidemment une fonction linéaire des q i ; posons:
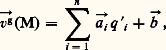

on voit immédiatement que, si:
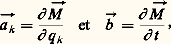
le terme non intégré est nul et il reste alors:
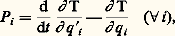
ce que nous supposerons par la suite.
Étudions maintenant le second membre:

on donne à Q i g le nom de coefficient énergétique (galiléen) relatif au paramètre q i . Dans le cas général, Q i s’écrit:
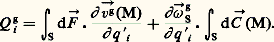
Remarquons que l’on peut exprimer Q i g en fonction de P g:
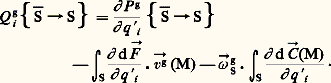
Les deux derniers termes non intégrés sont nuls lorsque le torseur des efforts extérieurs n’est pas exprimé explicitement en fonction des q i . Finalement, si:
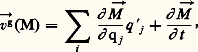
l’équation de Lagrange pour un solide unique s’écrit:
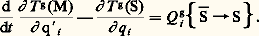
Équations de Lagrange pour un ensemble fini de solides
Soit un ensemble matériel , formé par la réunion de p solides Sj , dont la position par rapport au galiléen est repérée par n paramètres q i . On écrit d’abord l’équation de Lagrange pour chacun des Sj ; puis, par sommation, il vient:
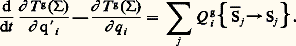
Pour un ensemble de solides, le coefficient énergétique fait intervenir les efforts extérieurs à l’ensemble et les interefforts entre les Sj .
Relation entre théorèmes généraux et équations de Lagrange
Pour un ensemble de solides, on a posé:
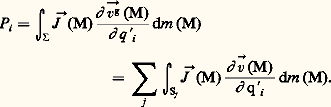
En désignant par Sj un point lié au solide Sj , on a, sur chaque Sj ,

en particulier, pour un solide unique S:
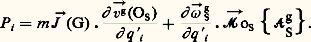
L’équation de Lagrange d’indice i est donc une combinaison linéaire des conséquences scalaires des théorèmes généraux, obtenues par projection sur les tangentes aux lignes coordonnées.
Le théorème de l’énergie-puissance n’est pas indépendant des équations de mouvement obtenues par les méthodes équivalentes des théorèmes généraux ou des équations de Lagrange mais peut être obtenu à partir de ces équations. L’équation donnée par ce théorème pourra donc remplacer une des équations de mouvement mais ne donne pas une équation supplémentaire.
4. Mouvement relatif
On appelle mouvement relatif tout mouvement d’un système matériel repéré par rapport à un repère quelconque () non galiléen. Les théorèmes de la mécanique en mouvement relatif se déduisent du principe fondamental, compte tenu de la formule de composition des accélérations qui permet d’écrire:

遼 ,e(,g) est le torseur défini par le champ des accélérations d’entraînement (de dans g ) et la mesure de masse, et 遼 ,C(,g) est le torseur défini par le champ des accélérations de Coriolis (de dans g) et la mesure de masse.
Quand il n’y a pas de confusion possible, on note simplement ces torseurs 遼e et 遼C.
Théorèmes généraux
Il vient immédiatement:

On donne en général le nom de torseurs des forces d’inertie d’entraînement 杻 size=1,e( size=1凞,g) et complémentaires 杻 size=1,C( size=1凞,g) aux opposés des torseurs 遼 size=1,e( size=1凞,g) et 遼 size=1,C( size=1凞,g).
La loi fondamentale donne alors:

D’où les théorèmes généraux en mouvement relatif:
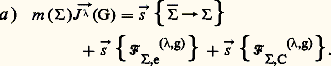
Pour tout ensemble matériel en mouvement par rapport à un repère quelconque, la quantité d’accélération de son centre d’inertie est égale à la somme du torseur des efforts extérieurs s’exerçant sur , augmentée des sommes du torseur des forces d’inertie d’entraînement et du torseur des forces d’inertie complémentaires dues au mouvement de par rapport au galiléen.

Pour tout ensemble matériel en mouvement par rapport à un repère quelconque, le moment dynamique en un point I quelconque est égal au moment, au même point I, du torseur des efforts extérieurs s’exerçant sur augmenté des moments en I du torseur des forces d’inertie d’entraînement et du torseur des forces d’inertie complémentaires dues au mouvement de par rapport au galiléen.
Théorème de l’énergie-puissance
Dans le cas du solide unique, on prend comme torseur 慄 le torseurS; on obtient donc:

or 杻 ,C(,g)S s’écrit aussi, si l’on tient compte de l’expression de l’accélération de Coriolis,

d’où:

Théorème . – Pour un solide unique S en mouvement par rapport à un repère quelconque, la dérivée par rapport au temps de l’énergie cinétique est égale à la puissance dans du torseur des efforts extérieurs s’exerçant sur S augmentée de la puissance dans des forces d’inertie d’entraînement dues au mouvement de par rapport à g.
Pour un ensemble fini de solides, on a, comme précédemment, par sommation,

Théorème . – Pour un ensemble fini de solides Sj en mouvement par rapport à un repère quelconque, la dérivée par rapport au temps de l’énergie cinétique est égale à la puissance dans des efforts extérieurs à Sj et des interefforts entre les Si augmentée de la puissance dans des forces d’inertie d’entraînement dues au mouvement de par rapport au galiléen.
Équations de Lagrange
Pour un solide unique, on choisit pour torseur 慄 le torseurS,i; il vient, compte tenu des résultats précédents et en prenant:

Pour un ensemble fini de solides, on a donc:

Pour le théorème de l’énergie-puissance en mouvement relatif, on a vu que l’accélération de Coriolis n’intervenait pas. Au contraire, le coefficient énergétique relatif aux forces d’inertie de Coriolis n’est en général pas nul lorsque l’on forme les équations de Lagrange en mouvement relatif pour un ensemble de solides.
En résumé, on peut dire que le principe fondamental (et, par suite, toutes ses conséquences) est encore valable pour le mouvement d’un ensemble matériel par rapport à un repère quelconque, à condition d’ajouter au torseur des forces extérieures s’exerçant sur l’ensemble matériel considéré le torseur des forces d’inertie d’entraînement et le torseur des forces d’inertie complémentaire.
5. Liaisons mécaniques s’exerçant sur un solide
La position par rapport à un repère () d’un système mécanique formé de s solides non rectilignes, de r solides rectilignes et de p points matériels dépend a priori de N = 6 s + 5 r + 3 p paramètres appelés paramètres primitifs du système par rapport à (). En général, ces paramètres ne sont pas indépendants et il existe des relations entre eux, leurs dérivées et le temps, relations indépendantes de l’étude dynamique et introduites par l’étude cinématique ou géométrique.
Étude cinématique et géométrique
Toute condition de contact entre deux solides introduit, par suite de l’indéformabilité, une liaison entre les paramètres primitifs. Par exemple, le contact d’une sphère de rayon R avec un plan est une liaison de caractère géométrique: le centre de la sphère est à la distance R du plan.
Si, de plus, la sphère est astreinte à rouler sans glisser sur le plan (ce qui se traduit en écrivant que la vitesse du point de la sphère au contact du plan est nulle par rapport à celui-ci), on a deux liaisons de type cinématique qui s’expriment par deux relations entre les paramètres et leurs dérivées premières par rapport au temps (cf. CINÉMATIQUE, chap. 7, «Chaînes usuelles de solides»). Plus généralement, une équation de liaison est dite holonome si elle ne fait intervenir que les paramètres (et éventuellement le temps). Une équation de liaison est dite non holonome si elle se présente sous la forme d’une fonction non intégrable des paramètres et de leurs dérivées premières. Cette distinction est essentielle lorsqu’on emploie la méthode de Lagrange.
Étude dynamique
On a été conduit à admettre que, chaque fois qu’on introduit une liaison dans un système, on introduit, du point de vue des forces, un torseur inconnu, dit torseur de liaison. Si l’on tient compte de l’équation de liaison, cela revient à faire intervenir cinq inconnues supplémentaires qui rendent indéterminés les problèmes de dynamique du solide lié. Pour lever cette indétermination, on a été amené à admettre des lois d’origine expérimentale, notamment des lois de frottement pour deux solides en contact.
Lois du frottement de deux solides en contact
Considérons le cas de deux solides S1 et S2 en contact ponctuel (on désigne par contact ponctuel un contact suivant une surface de mesure négligeable). Nous supposerons que ces deux solides sont limités par des surfaces ayant un plan tangent commun ( 神) bien défini au point de contact I. Désignons par n 21le vecteur unitaire de la normale commune à S2 et S1 en I dirigé de S2 vers S1 (fig. 1). Considérons le torseur distributeur des vitesses de S1 par rapport à un repère lié à S2 :
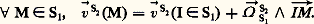
S2 (I 捻 S1) est la vitesse de glissement en I de S1 par rapport à S2 notée 轢 (S1/S2), c’est un vecteur situé dans le plan tangent commun.
行 ひ2S1 peut être décomposé par projection sur n 21et sur le plan ( 神):
Le torseur des actions exercées par S2 sur S1 est représenté par un torseurS2S1 dont les éléments de réduction en I peuvent être décomposés suivant leurs composantes dans ( 神) et sur n 21 轢; ainsi

Dans la plupart des schémas d’étude, 紐 神et 紐 n 轢, couples de résistance au roulement et au pivotement, peuvent être négligés. Nous ne donnerons que les lois du frottement de glissement relatives à び et ね (lois de Coulomb).
Deux cas sont à distinguer:
– Si 轢 (S1/S2) , on a, d’une part, び colinéaire à 轢 et de sens contraire, ce qu’on peut écrire:

et l’on a, d’autre part, |T 21 轢| = f |N 21 轢|, où f est un coefficient, sans dimension, dit coefficient réciproque de frottement de glissement (on dit souvent coefficient de frottement). Sa valeur dépend de nombreux paramètres; on peut cependant, au moins en première approximation, admettre qu’il ne dépend que des surfaces en contact mais qu’il est indépendant de 轢 (S1/S2) et de れS2S1. Dans le cas particulier où f est suffisamment faible pour être négligé (cas du non-frottement), on a T 21= ; la somme du torseur de contact est portée par la normale commune aux deux surfaces.
– Si 轢 (S1/S2) = , alors,

de plus, que 轢 soit nul ou non, si le contact est unilatéral, c’est-à-dire si, géométriquement, il peut y avoir rupture du contact, on sera assuré de la persistance du contact tant que N 21. n 21礪 0; c’est seulement si, à un instant, N 21. n 21= 0 qu’une rupture de contact peut se produire.
Dans le cas plus général où les deux solides S1 et S2 sont en contact suivant une surface, on admet qu’en chaque point de la surface de contact les lois de frottement précédentes sont encore valables; les actions de S1 sur S1 sont représentées par une densité vectorielle み (M) sur l’aire de contact 崙 et le torseurS2S1 est défini par ses éléments de réduction en un point quelconque Q par:

Applications des lois du frottement
Liaison glissière ou prismatique
Deux solides S1 et S2 sont liés par une liaison glissière si, et seulement si, les seuls mouvements possibles d’un des solides par rapport à l’autre sont les translations parallèles à une même direction. Les deux solides ont un degré de liberté l’un par rapport à l’autre.
Si le contact a lieu sans frottement entre les deux solides, les lois de Coulomb entraînent que le torseur d’action de contact a une somme géométrique normale à la direction de la translation; le moment a une direction quelconque.
Liaison cylindrique ou rotoïde
Deux solides S1 et S2 sont liés par une liaison cylindrique si les seuls mouvements possibles de S2 par rapport à S1 sont les rotations autour d’un axe lié aux deux solides.
Cette liaison peut être réalisée par le contact de deux surfaces de révolution de même axe, en exceptant, bien entendu, les cylindres et les sphères (fig. 2).
On peut aussi la réaliser au moyen de roulements à billes. Si le contact a lieu sans frottement, on déduit des lois de Coulomb que le torseur d’action de contact a un moment nul par rapport à l’axe de la liaison.
Liaison verrou
Deux solides S1 et S2 sont liés par une liaison verrou si, et seulement si, les seuls mouvements possibles de l’un des solides par rapport à l’autre sont les translations et les rotations autour d’un même axe (fig. 3). Chaque solide a deux degrés de liberté par rapport à l’autre solide. Cette liaison peut être réalisée par contact direct entre une surface cylindrique de révolution et une surface cylindrique de révolution de même axe et de même rayon située dans la première. Si le frottement qui a lieu au contact des deux surfaces est négligé, on déduit des lois de Coulomb que le torseur d’action de contact a une somme géométrique perpendiculaire à l’axe et un moment nul par rapport à cet axe.
Liaison sphérique
Deux solides S1 et S2 sont liés par une liaison sphérique si, et seulement si, un point 1 lié à S1 est astreint à rester à tout instant confondu avec un point 2 lié à S2. Les deux solides ont trois degrés de liberté l’un par rapport à l’autre.
On peut réaliser cette liaison au moyen de deux sphères de même rayon (noix et coquille), l’une liée à S2, l’autre à S1; cette réalisation est utilisée, par exemple, dans le levier de changement de vitesse des automobiles.
L’articulation sphérique peut aussi être réalisée au moyen de trois articulations rotoïdes d’axes concourants non coplanaires. C’est le dispositif de suspension «à la Cardan» utilisé, par exemple, dans le montage des rotors de gyroscope [cf. CINÉMATIQUE].
Si la liaison sphérique par contact direct (fig. 4) a lieu sans frottement, on a, d’après les lois de Coulomb, 紐 o索S2S1 = et れS2S1 inconnu (O désigne les points confondus 1 et 2). Dans la réalisation par organes intermédiaires, on montre que, si les trois liaisons rotoïdes sont sans frottement et si on peut négliger l’inertie des organes intermédiaires (armatures), alors le moment en O du torseur de liaison sur le rotor est encore nul (cf. CINÉMATIQUE, fig. 7).
Point de vue énergétique
Quel que soit le type de liaison envisagé, le théorème de l’action et de la réaction entraîne queS2S1 = 漣S1S2.
Solides en contact ponctuel en I
La puissance développée par les deux torseurs d’action de contactS2S1 etS1S2 est:
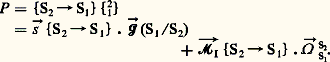
Si on néglige ぬIS2S1, il reste:

Cette puissance est nulle dans le cas où le frottement est négligeable ( れ orthogonal à 轢 ) et dans le cas où le mouvement s’effectue sans glissement en I (face=F0019 轢 = ).
Liaison quelconque sans frottement entre solides
On établit facilement que la puissance développée par l’ensemble des deux torseurs d’action de contact est nulle pour toute liaison sans frottement entre solides.
Définition . – On appelle liaison parfaite entre solides toute liaison telle que la puissance développée par l’ensemble des deux torseurs de liaison soit nulle.
Cette puissance est indépendante du repère, c’est pourquoi nous n’avons pas précisé ce dernier.
6. Fonction de force
Un torseur défini par une densité de forces sur un ensemble matériel est dit dérivé d’une fonction de force U si, et seulement si, il existe une fonction U (q 1, ..., q n ; t ) ne dépendant pas des q i et telle que, pour tout indice i , on ait:

De même, si sur un solide S on a une densité de torseur couple, celle-ci dérive d’une fonction de force U , s’il existe U (q 1, ..., q n ; t ) telle que:
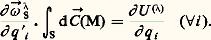
Voici trois exemples où ces considérations vont être appliquées respectivement au champ de pesanteur, aux efforts exercés par un ressort et aux forces gravitationnelles.
– Pour un ensemble matériel occupant une petite partie de l’espace, on admet que le champ de l’accélération de la pesanteur む est un champ uniforme. Le torseur des forces de pesanteur est alors un torseur vecteur dont la droite de moment nul passe par le centre d’inertie G de tel que:
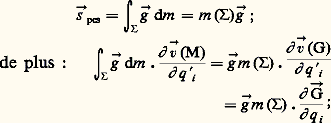
む étant indépendant des q i (champ uniforme), le torseur des forces de pesanteur dérive d’une fonction de force:

– Considérons uniquement le cas d’un ressort R, de masse négligeable travaillant en compression et en torsion. Désignons par l 0 la longueur naturelle du ressort, par k la constante d’élasticité et par C la constante de torsion. Les extrémités du ressort sont fixées respectivement aux points A de S1 et B de S2. Soit AB= x ゑ et S2S1 = ゑ ( est l’angle compté sur x dont S2 a tourné par rapport à S1),
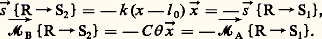
L’action du ressort sur l’ensemble des deux solides S1 et S2 dérive de la fonction de force:
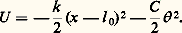
Si le ressort considéré ne travaille qu’à la traction-compression (ou à la torsion), il suffit dans les formules précédentes de faire C = 0 (ou k = 0).
– L’attraction newtonienne entre deux parcelles matérielles P et Q s’exprime par:

est la constante d’attraction newtonienne.
L’action newtonienne dérive de la fonction de force:

Pour l’attraction newtonienne de deux ensembles matériels 1 et 2, on a:

7. Intégrales premières des équations de la mécanique
Les équations de la mécanique déduites du principe fondamental forment un système de n équations différentielles du second ordre (que l’on peut toujours ramener à un système de 2 n équations différentielles du premier ordre) dont l’intégration dépend de 2 n constantes qui, dans un problème de mécanique, sont les conditions initiales, c’est-à-dire la donnée des q i (t 0) et des q i (t 0) à un instant t 0 pris comme instant initial.
On appelle intégrale première toute fonction f (q i , q i , t ) qui reste constante au cours du mouvement en vertu des équations déduites du principe fondamental exprimé sous l’une des formes suivantes: théorèmes généraux, théorème de l’énergie-puissance et équations de Lagrange. Donnons quelques exemples d’obtention d’intégrales premières.
Théorème de la somme géométrique .
Si ゎ désigne le vecteur unitaire d’un axe fixe dans le galiléen et si どg(G) 練 ゎ = 0, on a: g(G) 練 ゎ = constante (intégrale première).
Si どg(G) = , alors g(G) = ぢ, vecteur constant, ce qui fournit trois intégrales premières scalaires.
Théorème du moment dynamique .
Si ゎ 練 紐 I索 遼g size=1 = 0 et si, de plus, I est un point fixe dans le galiléen (ou le centre d’inertie de ), ゎ désignant le vecteur unitaire d’un axe fixe dans le galiléen, alors on peut écrire l’intégrale première ゎ 練 紐 I索p g size=1 = C te .
Si 紐 I索 遼g size=1 = et si I est un point fixe
dans le galiléen (ou le centre d’inertie de ), on en déduit 紐 I索p g size=1 = ぢ, vecteur constant dans le galiléen, et on obtient, par projection sur trois axes fixes dans (g), trois intégrales premières scalaires.
Théorème de l’énergie-puissance et théorème de Painlevé-Morel
Plaçons-nous dans le cas général où les liaisons dépendent du temps:

Alors, l’énergie cinétique a pour expression:
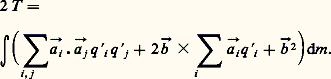
On peut distinguer dans cette fonction, respectivement, les ensembles de termes homogènes et de degré deux, un et zéro par rapport aux q k et écrire:

Le théorème de l’énergie s’écrit, pour un ensemble de solides,
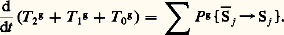
Prenons ici:
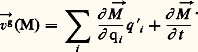
Les efforts extérieurs à et les interefforts entre les Si peuvent se décomposer en:
– un torseur inconnu maintenant la liaison dépendant du temps;
– un torseur d’actions de contact (de , avec des ensembles matériels extérieurs à , et des Si entre eux); ce torseur est en général inconnu;
– un torseur d’efforts connus, soit efforts extérieurs (par exemple la pesanteur), soit interefforts entre les Sj (attraction newtonienne, interactions électriques, etc.).
Un calcul direct montre que la puissance développée par le torseur qui maintient la liaison dépendant du temps est:
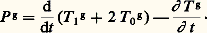
En utilisant ce premier résultat important, on obtient la formule fondamentale:
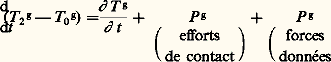
Les conditions suffisantes (mais qui ne sont évidemment pas nécessaires) souvent rencontrées en pratique pour que le théorème de l’énergie donne une intégrale première sont les suivantes:
– si la puissance des efforts de contact (des Si entre eux et de avec les ensembles matériels extérieurs à ) est nulle;
– si les forces données dérivent d’une fonction de forces U ;
– si T + U ne dépend pas explicitement du temps, on a:

ce qui donne l’intégrale première de Painlevé:

Lorsque les liaisons ne dépendent pas du temps, on obtient, comme cas particulier (compte tenu de T 0g 令 0) des conditions suffisantes d’existence de l’intégrale première de l’énergie cinétique,
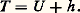
Équations de Lagrange
Si, pour un paramètre q k , on a

alors, l’équation de Lagrange correspondante donne l’intégrale première:
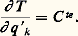
8. Galiléens approchés. Accélération de la pesanteur
Dans l’énoncé du principe fondamental, on a admis l’existence d’au moins un repère privilégié. Il faut maintenant le définir.
Considérant le système solaire comme isolé dans l’Univers, on prend comme repère absolu le repère ayant son origine au centre d’inertie du système solaire et dont les axes ont des directions fixes par rapport aux étoiles fixes (c’est-à-dire dont les distances angulaires apparaissent sensiblement constantes).
La classe des galiléens est définie par l’ensemble des repères en translation rectiligne et uniforme par rapport au repère absolu. Un tel mouvement ne pourra être mis en évidence expérimentalement.
Soit un repère ayant son origine au centre de la Terre et dont les axes ont des directions fixes par rapport aux étoiles. Un tel repère n’appartient pas à la classe des galiléens, le centre d’inertie GT de la Terre n’ayant pas, par rapport au repère absolu, un mouvement rectiligne et uniforme. En effet, désignant par m T la masse de la Terre et par み(M) la densité de force par unité de masse exercée sur la Terre par les autres corps du système solaire, le mouvement galiléen de GT est défini par l’équation:

Les distances qui séparent les corps du système solaire étant très grandes par rapport à celles qui entrent en jeu dans les expériences de mécanique à l’échelle humaine, on montre que, pour tout ensemble matériel situé dans l’environnement de la Terre, on peut admettre, avec une précision supérieure à celle des mesures, qu’un repère ayant son origine au centre de la Terre et dont les axes ont des directions fixes par rapport aux étoiles est galiléen, si l’on convient de négliger les forces extraterrestres.
Considérons maintenant un repère RT lié à la Terre. Par rapport au repère précédemment défini, le repère RT a un mouvement de rotation que l’on peut admettre uniforme autour de la ligne des pôles:
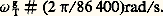
Pour tenir compte du fait que RT n’est pas galiléen, il faut donc introduire les forces d’inertie d’entraînement et complémentaire (théorie du mouvement relatif) dues à la rotation de la Terre sur elle-même. En pratique, l’accélération む de la pesanteur est la résultante de l’accélération newtonienne due à la Terre et de l’accélération d’entraînement due à la rotation de la Terre sur elle-même, changée de signe; il suffit donc d’ajouter aux forces de pesanteur uniquement les forces d’inertie de Coriolis. Remarquons qu’au voisinage de la Terre le terme provenant des forces d’inertie de Coriolis dues à la rotation de la Terre sur elle-même est très souvent négligeable devant les forces de pesanteur (cf. CINÉMATIQUE, tabl. 2); ces forces de Coriolis n’interviendront que pour des mouvements très rapides (par exemple rotor de gyroscope) ou pour des mouvements que l’on suit pendant longtemps avec précision.
La Terre pouvant être considérée sensiblement comme une sphère pleine formée de couches concentriques homogènes, l’attraction newtonienne qu’elle exerce est la même en tous les points de sa surface, mais l’accélération d’entraînement due à sa rotation sur elle-même est une fonction de la latitude du lieu considéré. L’intensité g de l’accélération de la pesanteur varie donc suivant la latitude: elle est différente à l’équateur (g = 9,7803 m/s2) et au pôle (g = 9,832 2 m/s2).
9. Équilibres absolus et relatifs
On dit qu’un ensemble matériel est en équilibre par rapport à un repère () lorsque tous les paramètres q i repérant la position de par rapport à () restent constants au cours du temps, q i = q i ,e étant solution de toutes les équations de mouvement, avec les conditions initiales q i (t 0) = q i ,e et q i (t 0) = 0.
Puisque les équations générales du mouvement sont:
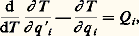
les positions d’équilibre, si elles existent, sont déterminées par les valeurs q i ,e des n paramètres constituant une solution des n équations:

Dans le cas où il n’y a pas de liaison dépendant du temps (T 0 令 0) et où toutes les forces dérivent d’une fonction de forces U , les positions d’équilibre sont solutions des n équations:

Si certains seulement des q i restent constants au cours du temps, il existe un équilibre par rapport à ces paramètres (équilibre relatif), mais il n’y a pas de position d’équilibre pour le système.
Stabilité d’un équilibre
Par définition, on dit qu’une valeur q i ,e d’équilibre pour un paramètre q i est stable si, et seulement si, quels que soient 﨎 礪 0 et 﨎 礪 0 suffisamment petits:
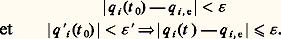
Une position d’équilibre d’un ensemble matériel par rapport à un repère () sera dite stable si, et seulement si, il y a stabilité par rapport à tous les paramètres.
Pratiquement, une position d’équilibre instable ne pourra jamais être mise en évidence, d’où l’importance de savoir reconnaître la stabilité d’une position d’équilibre.
Dans le cas où toutes les forces dérivent d’une fonction de forces indépendantes du temps, où il n’y a pas de liaison dépendant du temps et où la fonction de forces U dépend de tous les paramètres q i , on a vu que les valeurs des q i ,e sont celles qui rendent U extremum. On est assuré de la stabilité de l’équilibre (théorème de Lejeune-Dirichlet) si cet extremum est un maximum (maximum relatif strict).
Dans le cas général, on linéarise les équations du mouvement au voisinage de la position d’équilibre considérée, puis on étudie la stabilité du sytème linéarisé, d’où l’on déduit la stabilité de la position d’équilibre.
Technique de linéarisation
Les équations de mouvement d’un système mécanique, à n degrés de liberté, sont de la forme:

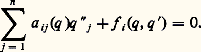
La position d’équilibre peut toujours être obtenue pour q 1 = q 2 = ... = q n = 0 ou en faisant un changement de variables.
La position d’équilibre correspond à f i (0, 0) = 0.
Le système linéarisé au voisinage de la position d’équilibre q = 0 est, par définition, le système des n équations différentielles, linéaires, du second ordre, à coefficients constants:
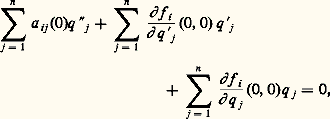
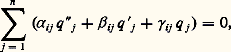
Équation caractéristique et stabilité
D’après la théorie des équations différentielles, le système linéarisé précédent possède des solutions particulières de la forme q j = A j exp st où s et les A j sont inconnus. Si ces valeurs des q j sont reportées dans le système linéarisé, celui-ci se présente comme un système de n équations du premier degré par rapport aux n inconnues A j . Ce système n’admet de solution autre que zéro, pour tous les A j , que si le déterminant des coefficients est nul:
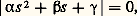
où 見, 廓, 塚 représentent les matrices dont les éléments sont respectivement les 見 ij , 廓 ij et 塚 ij . Cette équation de degré 2 n par rapport à s est l’équation caractéristique qui admet donc 2 n racines (réelles ou non). La solution générale du système linéarisé est une superposition de toutes les solutions particulières et elle s’écrit:
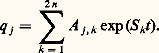
Une condition nécessaire de stabilité du système linéarisé est qu’aucune des racines S k de l’équation caractéristique ne soit à partie réelle positive (qui donnerait un terme croissant exponentiellement avec le temps, d’où instabilité).
Considérons par exemple un système linéarisé de la forme:

L’équation caractéristique s’écrit:

équation bicarrée en s . Pour que cette équation n’ait aucune de ses racines à partie réelle positive, il faut et il suffit que l’équation du second degré:

ait ses deux racines réelles et négatives; cette condition sera satisfaite si:

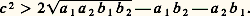
– dans le cas où c = 0 (c’est-à-dire si l’on supprime le terme de couplage gyroscopique), le système linéarisé considéré ici est instable;
– dans le cas où c 2 est suffisamment grand (couplage gyroscopique assez intense), le système linéarisé peut devenir stable.
Si b 1 et b 2 sont de signes contraires, le système linéarisé sera toujours instable, quel que soit c .
Si b 1 et b 2 sont du même signe que a 1 et a 2, le système linéarisé sera toujours stable, quel que soit c .
10. Autres applications du principe fondamental
En donnant au principe fondamental une forme équivalente, mais légèrement différente, on peut montrer son application à un cas de la dynamique des systèmes «à masse variable» puis à la dynamique des chocs.
Auparavant, il faut définir la dérivée d’un torseur par rapport au temps t dans un repère ().
La dérivée du torseur 淪 dépendant de t dans le repère () est, par définition, le torseur noté:
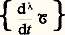
ou plus simplement 淪 . Les éléments de réduction du torseur 淪 , en un point P size=1凞 dont la situation dans () ne dépend pas de t , sont:

On vérifie immédiatement que le moment de 淪 , en un point Q dont la situation dans () dépend de t , est:

Nouvel énoncé du principe fondamental
Il existe au moins un repère dit galiléen (ou absolu) et une chronologie absolue tels que, pour tout ensemble matériel , la dérivée par rapport au temps dans le repère galiléen du torseur des quantités de mouvement galiléen est égale au torseur des efforts extérieurs s’exerçant sur cet ensemble:

Cet énoncé est équivalent au précédent; car, compte tenu de la définition de la dérivée d’un torseur, le torseur:
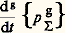
admet, comme éléments de réduction en Q,
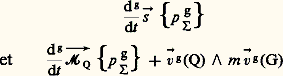
qui sont aussi [cf. CINÉTIQUE] les éléments de réduction en Q de 遼g size=1.
Mouvement de translation d’une fusée
La propulsion d’une fusée étant une propulsion par réaction, l’émission des gaz est trop importante pour que la masse de la fusée (constituée de l’enveloppe et des combustibles non consommés) puisse être considérée comme constante. Le principe fondamental s’applique à un ensemble matériel bien déterminé et dont les constituants sont suivis dans leurs mouvements. La fusée étant par hypothèse en translation, on admet que tous ses points, et en particulier son centre d’inertie G, ont tous la même vitesse g(t ) à une date donnée t . On admet que chaque particule de gaz éjecté a, à la date t , la même vitesse ゐ (t ) par rapport à l’enveloppe.
Considérons, à l’instant t , l’ensemble matériel , formé par l’enveloppe et le combustible intérieur à l’enveloppe jusqu’à sa section droite arrière; la quantité de mouvement de cet ensemble est, à la date t ,
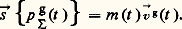
Pendant l’intervalle de temps (t , t + t ), une certaine masse de gaz (face=F0019 漣 m ) est brûlée, de telle sorte que la masse de la fusée jusqu’à la section droite arrière de l’enveloppe est, à l’instant t + t , m (t ) + m , alors que la vitesse de translation de la fusée a pour valeur (t ) + . À l’instant t + t , la somme géométrique du torseur cinétique du même ensemble matériel que celui considéré à la date t est devenue:



Le théorème de la somme dynamique donne, pour le mouvement de translation d’une fusée propulsée par réaction,

L’éjection de gaz se traduit donc par la force:

dirigée vers l’avant de l’engin; c’est la force de propulsion.
Dans la somme géométrique des forces extérieures, on néglige, à cause de la faible pression, l’action des gaz éjectés sur la fusée.
Dynamique des chocs
On dit qu’au cours du mouvement d’un système matériel se produit un choc si, en un intervalle de temps infiniment court t = t 1 漣 t 0, les vitesses des différents points du système subissent une variation finie.
Dans la théorie approchée de la dynamique des chocs, on ne tient pas compte des effets thermiques et des déformations de solides qui accompagnent toujours ces phénomènes; de plus, on néglige les termes de l’ordre de grandeur de t en ne conservant que les termes finis (de l’ordre de la variation des vitesses).
Il s’ensuit qu’en dynamique des chocs on négligera les variations des paramètres de position au cours du choc. Si t 0 représente l’instant de début du choc et t 1 l’instant de fin du choc, on aura, pour tout paramètre, q i (t 1 ) = q i (t 0).
Si l’on écrit le principe fondamental sous la forme:

et si l’on intègre cette relation entre les instants t 0 et t 1 de début et de fin de choc, il vient:
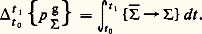
Par définition,
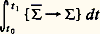
est le torseur des percussions extérieures s’exerçant sur .
D’où l’énoncé fondamental concernant les phénomènes de chocs:
Pendant l’intervalle de temps très court d’un choc, la variation du torseur des quantités de mouvement galiléennes d’un ensemble matériel quelconque est égale au torseur 戮 des percussions extérieures à :
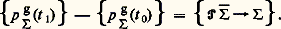
On en déduit immédiatement les deux théorèmes suivants entre vecteurs:
Théorème I. Pendant l’intervalle de temps très court d’un choc, la variation de la quantité de mouvement galiléenne d’un ensemble matériel est égale à la somme du torseur des percussions extérieures à :
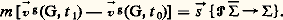
Théorème II . Pendant l’intervalle de temps très court d’un choc, la variation du moment en un point I quelconque du torseur cinétique galiléen d’un ensemble matériel est égale au moment en ce point du torseur des percussions extérieures à :

Comme on l’a vu, le torseur des percussions extérieures à un ensemble matériel 戮 est par définition:

sa définition fait donc intervenir tous les torseurs d’efforts extérieurs à . Mais tout torseur d’effort fini (c’est-à-dire dont les composantes restent finies) donnera un torseur de percussion que l’on néglige (terme infiniment petit) suivant la convention adoptée dans la théorie. Il en sera ainsi, en particulier, du torseur des forces de pesanteur.
Toutefois, si on est en présence d’un torseur d’effort inconnu, on doit toujours lui associer un torseur de percussion; c’est le cas notamment pour les torseurs d’effort de liaison entre solides.
En ce qui concerne les liaisons entre solides, on admet que les lois de Coulomb relatives au frottement de glissement sont encore valables pendant l’intervalle (t 0, t 1) d’un choc. Donc, dans le cas de liaison (rotoïde, sphérique, etc.) entre solides, si la liaison a lieu sans frottement, les torseurs de percussion présentent les mêmes particularités que les torseurs d’efforts correspondants.
Les problèmes que se propose de résoudre la dynamique des chocs ne sont évidemment pas la détermination du mouvement mais: – soit la détermination de l’état des vitesses à l’instant t 1 de la fin du choc, connaissant l’état des vitesses à l’instant t 0 de début du choc,
– soit la détermination de torseurs de percussions de liaison.
Dans le cas de liaison entre solides existant pendant le choc et ne persistant pas à la fin du choc, le principe fondamental et les lois du frottement ne suffisent plus à déterminer entièrement le problème. C’est, par exemple, le cas d’une boule rigide indéformable rebondissant sur un mur, le contact étant supposé sans frottement; le principe fondamental donne six équations scalaires pour sept inconnues: les six q i (t 1) et la composante de la percussion due à l’action du mur et normale à celui-ci.
Pour lever cette indétermination, on a été amené à introduire un coefficient empirique dit coefficient de restitution e (0 諒e 諒 1), reliant les composantes normales des vitesses des points en contact sur chacun des solides en début et en fin de choc. Les cas limites e = 0 et e = 1 correspondent respectivement au choc mou (contact persistant en fin de choc) et au choc parfaitement élastique.
dynamique [ dinamik ] adj. et n. f.
• 1692; gr. dunamikos, de dunamis « force »
I ♦ Adj.
1 ♦ Relatif aux forces, à la notion de force. « Traité de la science dynamique », de Leibniz.
♢ (1947) Écon. Relatif à l'étude des faits économiques dans leurs causes et leurs effets (opposé à statique). Économie dynamique. Théorie dynamique de l'économie.
♢ Méd. Relatif à l'efficacité, la puissance d'action d'un remède. ⇒ dynamisation.
2 ♦ Qui considère les choses dans leur mouvement, leur devenir. Représentation dynamique d'un objet. — Par ext. Qui suggère le mouvement. Publicité dynamique.
3 ♦ (XXe) Cour. Qui manifeste une grande vitalité, de la décision et de l'entrain. Une personne dynamique. ⇒ actif, énergique, entreprenant; fam. 3. battant, fonceur, remonté. Un jeune cadre dynamique.
II ♦ N. f.
1 ♦ (1752) Phys. Branche de la mécanique qui étudie le mouvement d'un mobile considéré dans ses rapports avec les forces qui en sont les causes. ⇒ accélération, force. Lois, équations de la dynamique.
♢ (XXe) Ensemble des forces en interaction et en opposition dans un phénomène, une structure (⇒aussi dialectique). Dynamique du système. — (v. 1965) Fig. Forces orientées vers un progrès, un développement. Créer une dynamique. Dynamique de l'idée européenne. Dynamique révolutionnaire.
2 ♦ Sociol. Partie de la sociologie qui étudie les faits en évolution et non dans leur état actuel. Dynamique sociale, terme employé par Comte, par opposition à statique sociale. Dynamique des sociétés. — Dynamique des populations : étude de l'évolution de la structure des populations (⇒ démographie) .
3 ♦ (v. 1940) Psychol., sociol. Dynamique de(s) groupe(s) : ensemble des règles qui président à la conduite des groupes sociaux dans le cadre de leur activité propre.
♢ Psychan. Dynamique de l'appareil psychique.
4 ♦ Rapport, écart entre les niveaux extrêmes (du plus fort au plus faible) d'une grandeur physique. La dynamique d'un signal s'exprime en décibels.
⊗ CONTR. Statique. Apathique.
● dynamique adjectif (grec dunamikos) Relatif à la force, au mouvement, à la dynamique. Qui considère les phénomènes dans leur évolution dans le temps : Une perspective dynamique de la langue. Qui manifeste de l'énergie et de l'efficacité ; actif, énergique : Un vendeur dynamique. Se dit d'un art caractérisé par l'énergie et le mouvement. Se dit de l'aspect sous lequel on envisage les phénomènes psychiques comme résultant de la composition des forces pulsionnelles conflictuelles. ● dynamique (expressions) adjectif (grec dunamikos) Accent dynamique, en phonétique, accent caractérisé essentiellement par une prééminence de l'intensité. Analyse dynamique, analyse des relations entre variables économiques au cours du temps. (Elle s'est surtout développée à partir de 1930 sous l'influence des Suédois.) ● dynamique (synonymes) adjectif (grec dunamikos) Qui manifeste de l'énergie et de l'efficacité ; actif, énergique
Synonymes :
- actif
- énergique
Contraires :
- indolent
- mou
● dynamique
nom féminin
Partie de la mécanique qui s'occupe des relations entre les forces et les mouvements qu'elles produisent.
Ensemble de forces qui entraînent, provoquent un mouvement, une évolution à l'intérieur d'une structure en développement : La dynamique révolutionnaire.
Économie
Analyse dynamique des faits économiques.
Électroacoustique et Télécommunications
Rapport du niveau moyen maximal au niveau moyen minimal de la puissance d'un signal, ces niveaux étant exprimés en général en décibels.
● dynamique (expressions)
nom féminin
Dynamique statistique, méthode d'étude du comportement dynamique des systèmes sous l'effet des signaux de commande et des perturbations auxquels ils sont soumis.
Dynamique d'une chaîne électroacoustique, différence entre le niveau maximal et le niveau minimal du signal transmis par une chaîne électroacoustique dans des conditions de fonctionnement normal.
Dynamique globale, synonyme de géodynamique.
Dynamique fluviale, partie de l'hydrographie fluviale qui a pour objet l'étude des courants fluviaux, de leur force érosive, du transport des matériaux.
Dynamique de groupe, lois empiriques régissant le comportement d'un groupe défini et fondées sur la constatation d'un système d'interdépendance entre ses membres. (Issue des théories de K. Lewin, elle a particulièrement été étudiée dans le domaine du leadership, celui de la conformité, et dans les processus d'influence.)
Dynamique sociale, selon A. Comte, partie de la sociologie qui étudie les changements ou les étapes successives dans l'évolution des faits sociaux.
● dynamique (synonymes)
nom féminin
Géophysique. Dynamique globale
Synonymes :
- géodynamique
dynamique
adj. et n. f.
rI./r adj.
d1./d Relatif aux forces, et aux mouvements qu'elles engendrent. électricité dynamique: courant électrique (par oppos. à électricité statique).
d2./d Fig. Qui manifeste une force, une puissance engendrant un mouvement. Art dynamique. Ant. statique.
d3./d Fig. Qui manifeste de l'énergie, de l'entrain, de la vitalité. Un chef d'équipe dynamique.
rII./r n. f.
d1./d MECA Partie de la mécanique qui traite des relations entre les forces et des systèmes sur lesquels ces forces agissent.
d2./d PSYCHO Dynamique de(s) groupe(s): étude expérimentale des lois qui régissent le comportement des petits groupes et des individus au sein de ces groupes.
— Ensemble des techniques thérapeutiques liées à l'influence du groupe sur le comportement de l'individu (ou celui du groupe).
⇒DYNAMIQUE, adj. et subst. fém.
I.— Adjectif
A.— [Relatif au mouvement]
1. PHYS. Relatif au mouvement produit par des forces. Effet, effort, équilibre, processus, résultante, schème, système, tension dynamique. Anton. statique :
• 1. Le rendement (...) de la pompe s'obtient (...) en multipliant le rendement dynamique (...) par deux coefficients de réduction, correspondant, l'un aux frottements mécaniques de l'arbre, le second aux fuites.
HATON DE LA GOUPILLIÈRE, Cours d'exploitation des mines, 1905, p. 438.
— Spécialement
a) MUS. Relatif aux différences d'intensité. Mélodie dynamique; phénomènes dynamiques et rythmiques. Si les moyens purement musicaux d'effectuer cette rentrée sont innombrables, il n'y a que deux procédés dynamiques : le crescendo et le diminuendo (DUPRÉ, Improvis. orgue, 1925, p. 113).
SYNT. Composition, contraste, élément, expansion, procédé dynamique.
b) LING. Accent dynamique. ,,Accent dont la composante essentielle est constituée par une intensité supérieure affectant la syllabe accentuée`` (MOUNIN 1974). Anton. accent tonique.
2. PHILOS. et SC. Qui considère les choses dans leur mouvement. Conception, idée, morale, point de vue, vérité dynamique. Anton. adynamique, mécanique, statique :
• 2. Un effort plus scientifique a été fait depuis lors, à la recherche des composantes raciales du psychisme. Il n'est devenu fructueux que lorsqu'on a abandonné la méthode statistique inventoriale, pour une conception dynamique du portrait racial.
MOUNIER, Traité du caractère, 1946, p. 158.
♦ Économie dynamique. Qui cherche à expliquer les faits économiques dans leurs causes et leurs effets. Théorie dynamique de l'économie (ROB. Suppl. 1970).
♦ Météorologie dynamique. Qui cherche à dégager les régularités des mouvements de l'atmosphère et à mettre ces mouvements en rapport avec les phénomènes immédiatement observables.
♦ Psychologie dynamique. Qui étudie les processus psychiques dans leur évolution. La psychologie dite dynamique n'ignore souvent pas moins que le vieil empirisme ce qu'est une conscience (RICŒUR, Philos. volonté, 1949, p. 41).
♦ Sociologie dynamique. Cf. dynamique sociale (infra II B 2 rem.).
B.— [En parlant de la vie mentale] Qui procède par modifications incessantes selon une finalité; qui se développe. Imagination, joie, pensée dynamique. Anton. statique. La psychologie et la sociologie du nouvel organicisme doivent faire appel (...) à un principe authentiquement créateur, à un inconscient dynamique et à une société ouverte (J. VUILLEMIN, Être et trav., 1949, p. 79).
— Emploi subst. masc. Ce qui est en développement, se modifie selon une finalité. Ces états anormaux, leur ressemblance et parfois sans doute aussi leur participation à des états morbides, se comprendront sans peine si l'on pense au bouleversement qu'est le passage du statique au dynamique, du clos à l'ouvert (BERGSON, Deux sources, 1932, p. 243).
C.— Usuel. [En parlant de pers.] Qui est plein de vitalité. Jeune cadre, entrepreneur dynamique. Synon. actif, entreprenant; anton. apathique, mou. Le général Platt, chef alerte et dynamique (DE GAULLE, Mém. guerre, 1954, p. 146). La Norvège a été le premier petit pays européen à se lancer dans un programme atomique notable sous l'impulsion dynamique du physicien Gunnar Randers (GOLDSCHMIDT, Avent. atom., 1962, p. 151).
— P. anal. Économie, gouvernement, société dynamique.
II.— Subst. fém.
A.— 1. Mouvement interne qui anime et fait évoluer (quelque chose). La dynamique des classes. Anton. statique. Une dynamique complète peut être tirée de l'effet de domination. Le jour où elle serait entièrement élaborée, elle mériterait peut-être le nom de « dynamique de l'inégalité » (PERROUX, Écon. XXe s., 1964, p. 36) :
• 3. Sur la statique immémoriale de l'art s'ébauchait une dynamique, faite non plus de l'instantané pétrifié du mouvement, mais de la suggestion de son déploiement.
HUYGHE, Dialogue avec le visible, 1955, p. 150.
SYNT. Dynamique bienfaisante, cohérente, partielle, totale; dynamique des âges, des états, des firmes.
2. Spécialement
a) MUS. Écart de niveau sonore entre les passages les plus forts et les plus faibles d'une œuvre musicale. Peut-être en effet qu'il ne suffit pas de réaliser des tracés de hauteur, de dynamique, et de timbre, sur un enregistrement (SCHAEFFER, Rech. mus. concr., 1952, p. 187).
b) RADIO. ,,Écart exprimé en décibels entre les niveaux les plus forts et les plus faibles d'un signal utile`` (Radio 1972).
c) Dynamique de groupe; dynamique sociale (cf. infra B 2). Moreno semble ignorer la « dynamique des groupes », c'est-à-dire cet ensemble de polarisations et de tendances qui naissent de la vie du groupe et non pas des « instincts » individuels (Traité sociol., 1968, p. 250).
B.— [Étude du mouvement]
1. PHYS. Partie de la mécanique qui étudie les relations entre les forces et les mouvements qu'elles produisent. La dynamique classique, newtonienne, relativiste. Anton. statique :
• 4. Quelques formules, pensait-on, devaient résumer toute notre expérience, et un tableau final de relations d'équilibre et de transformations, analogue ou identique à celui que forment les équations de la dynamique devait être le but et le terme du travail de l'intelligence scientifique.
VALÉRY, Variété V, 1944, p. 60.
2. Domaine des sc.
— ASTRON. Dynamique stellaire. Étude des systèmes stellaires dans leur dynamisme évolutif (d'apr. Astron. 1973).
— GÉOL. Dynamique des sols. ,,Étude des sols considérés au point de vue des forces qui en commandent la formation et l'évolution`` (PLAIS.-CAILL. 1958).
— GÉOGR. Dynamique des populations. ,,Étude de l'évolution de la structure des populations dans l'espace et dans le temps`` (DAGET-GODRON 1974).
— SOCIOLOGIE
♦ Dynamique sociale. Étude des forces créatrices auxquelles on attribue une valeur causale dans l'évolution et le progrès des sociétés. La dynamique sociale étudie, à la manière de la physiologie, la vie en mouvement, les forces créatrices du devenir et du progrès (BIROU 1966).
♦ Dynamique de groupe. ,,Étude des lois qui régissent les phénomènes spécifiques des groupes restreints, les changements personnels à l'intérieur des groupes`` (MUCCH. Sc. soc. 1969).
Rem. Dans la plupart des cas, ces synt. désignent aussi l'obj. d'étude; dynamique correspond alors au sens II A.
Prononc. et Orth. :[dinamik]. Ds Ac. 1762-1932. Étymol. et Hist. A. Adj. 1. a) 1692 mécan. science dynamique « science des forces ou puissances qui meuvent les corps » (LEIBNITZ, Traité de la sc. dynamique, Lett. à Pellisson ds DG); b) 1842 fig. véhémence dynamique (SAINTE-BEUVE, Port-Royal, t. 3, p. 174); 1934 « entraînant » (Candide in Galliot, 141 ds QUEM. Fichier); 2. 1852 philos. sociologie dynamique « qui étudie la vie en mouvement, les forces créatrices du devenir, le progrès » (COMTE, Catéch. posit., p. 139); 3. 1864 peintre dynamique « caractérisé par la puissance et le mouvement » (GONCOURT, Journal, p. 62). B. Subst. 1752 mécan. (Trév.); 1833 la dynamique intérieure de l'homme (BALZAC, Théor. démarche, p. 623). Empr. au gr.  « fort, puissant ». Fréq. abs. littér. :405. Fréq. rel. littér. :XIXe s. : a) 59, b) 412; XXe s. : a) 303, b) 1 267. Bbg. GALL. 1955, p. 141. — PAMART (P.). Esquisse du vocab. de l'audio-visuel. Vie Lang. 1973, p. 193. — SCHMIDT (H.). Fr. vivant. Rech. lexicol. Praxis. 1970, t. 17, pp. 72-74.
« fort, puissant ». Fréq. abs. littér. :405. Fréq. rel. littér. :XIXe s. : a) 59, b) 412; XXe s. : a) 303, b) 1 267. Bbg. GALL. 1955, p. 141. — PAMART (P.). Esquisse du vocab. de l'audio-visuel. Vie Lang. 1973, p. 193. — SCHMIDT (H.). Fr. vivant. Rech. lexicol. Praxis. 1970, t. 17, pp. 72-74.
 « fort, puissant ». Fréq. abs. littér. :405. Fréq. rel. littér. :XIXe s. : a) 59, b) 412; XXe s. : a) 303, b) 1 267. Bbg. GALL. 1955, p. 141. — PAMART (P.). Esquisse du vocab. de l'audio-visuel. Vie Lang. 1973, p. 193. — SCHMIDT (H.). Fr. vivant. Rech. lexicol. Praxis. 1970, t. 17, pp. 72-74.
« fort, puissant ». Fréq. abs. littér. :405. Fréq. rel. littér. :XIXe s. : a) 59, b) 412; XXe s. : a) 303, b) 1 267. Bbg. GALL. 1955, p. 141. — PAMART (P.). Esquisse du vocab. de l'audio-visuel. Vie Lang. 1973, p. 193. — SCHMIDT (H.). Fr. vivant. Rech. lexicol. Praxis. 1970, t. 17, pp. 72-74.
dynamique [dinamik] adj. et n.
ÉTYM. 1692, science dynamique; grec dunamikos, de dunamis « force ».
❖
———
1 Adj. Relatif aux forces, à la notion de force. || Traité de la science dynamique, œuvre de Leibniz. — Mécan. || Effet dynamique. || Électricité dynamique, courant électrique; son étude. || Unité dynamique. ⇒ Dyne.
♦ Écon. (par oppos. à statique). Relatif à l'étude des faits économiques dans leurs causes et leurs effets. || Théorie dynamique de l'Économie. || L'Économie dynamique tient compte de la chronologie des faits économiques dans les relations de causes à effets (analyse économique).
1 (…) on peut qualifier de dynamique une théorie lorsque celle-ci vise à l'interprétation d'une situation qui résulte d'influences produites à des époques différentes et manifestées à un même moment ou provoquées à la même date, mais successivement ressenties.
Jean Romeuf, Dict. des sciences économiques, t. I, p. 431.
♦ Méd. Relatif à l'efficacité, à la puissance d'action d'un remède. ⇒ Dynamisation.
2 Par un procédé qui lui est propre, et qu'on n'avait jamais essayé avant elle, la médecine homéopathique développe tellement les vertus médicinales dynamiques des substances grossières, qu'elle procure une action des plus pénétrantes à toutes, même à celles qui, avant d'avoir été traitées ainsi, n'exerçaient pas la moindre influence médicamenteuse sur le corps de l'homme.
P. Vannier, l'Homéopathie, p. 31.
2 Sc. Qui considère les choses dans leur mouvement, leur devenir.
3 Une fois de plus, il distingue une religion statique et une religion dynamique, le tout fait et le « se faisant », le discours et la réalité.
A. Maurois, Études littéraires, Bergson, IV, t. I, p. 176.
3 (XXe). Cour. (Personnes). Qui manifeste une grande vitalité, de la décision et de l'entrain. || Une personne dynamique. ⇒ Dynamisme (plein de dynamisme); actif, énergique, entreprenant. || Elle est plus dynamique que ses enfants. || Un jeune cadre dynamique. || Un vendeur dynamique et combatif. ⇒ Accrocheur, agressif.
3.1 Dîner, le soir, avec deux des organisateurs, genre « abbés dynamiques ».
F. Mauriac, Bloc-notes 1952-1957, p. 30.
———
II N. f.
1 Mécan. || La dynamique : partie de la mécanique qui étudie le mouvement d'un mobile considéré dans ses rapports avec les forces qui en sont les causes. ⇒ Accélération, force. || La plupart des problèmes de dynamique se ramènent à la résolution d'un système d'équations différentielles.
♦ (XXe). Ensemble des forces en interaction et en opposition dans un phénomène, une structure. || Dynamique du système. (Géol.). || Dynamique des sols. — Dynamique des populations. — (V. 1965). Fig. Forces orientées vers un progrès, une expansion. || La dynamique de l'idée européenne. || Dynamique révolutionnaire. || La dynamique politique (→ 1. Politique, cit. 12).
2 Sociol. Partie de la sociologie qui étudie les faits en évolution et non dans leur état actuel. || Dynamique sociale (ou sociologie dynamique), terme employé par A. Comte, par oppos à statique sociale. || Dynamique des sociétés. || « L'État-Nation (…) ressuscite les formes de la pensée, de la politique et de la dynamique tribales » (G. Bouthoul, Sociologie de la politique, p. 33).
4 La dynamique sociale a pour objet de montrer le progrès des organes nécessaires dans la structure de toute société, et qui existe dans les trois états.
J. Baudry, Cours, in J. Romeuf, Dict. des sciences économiques, t. I, p. 432.
➪ tableau Noms de sciences et d'activités à caractère scientifique.
3 (V. 1940, en angl., in K. Lewin). Psychol., sociol. || Dynamique de groupe; dynamique des groupes : ensemble des règles qui président à la conduite de groupes sociaux dans le cadre de leur activité propre. || Influence de la dynamique des groupes sur le rendement. || Utilisation des diverses sciences humaines (→ ci-dessous, psychan.) dans la dynamique des groupes. || Spécialiste de la dynamique sociale. ⇒ Dynamicien.
5 L'un de ces buts (de la psychologie sociale) est l'étude des relations inter-individuelles et de la dynamique des groupes. Il faut d'abord rappeler les travaux de Lewin et de ses collaborateurs sur les « champs » perceptifs et affectifs (en un sens gestaltiste élargi, comprenant le sujet et ses réactions), et surtout sur la dynamique d'ensemble de ces champs; Lewin s'est efforcé de montrer que les caractères de désirabilité, les oppositions ou les inhibitions et « barrières psychiques », dépendent de la structure d'ensemble du champ autant que des besoins plus permanents des individus.
J. Piaget, Épistémologie des sciences de l'homme, p. 174-175.
♦ Psychan. || Dynamique des états de conscience. « Aspect de la théorie psychanalytique selon lequel les processus de conduite sont envisagés comme résultant de l'interaction et de l'opposition des forces » (D. Lagache, in Piéron, Vocabulaire de la psychologie).
4 Écart de niveau sonore entre extrêmes, du plus fort au plus faible. || La dynamique d'un passage musical. — Écart (en décibels) entre les niveaux extrêmes d'un signal utile (radio, reproduction sonore). || La dynamique d'un disque.
❖
DÉR. Dynamicien, dynamiquement.
COMP. Électrodynamique, isodynamique, magnétodynamique, thermodynamique.
Encyclopédie Universelle. 2012.