Akademik

HYDROLOGIE

Étymologiquement, l’hydrologie est la science de l’eau. Molécule, gaz, liquide ou solide, l’eau voit son étude ressortir à la physique et à la chimie. C’est à l’étude de l’eau dans la nature, où s’expriment évidemment ses propriétés physico-chimiques, qu’est consacrée l’hydrologie. L’eau apparaît dans la nature sous des formes et selon des rythmes extraordinairement diversifiés, mais toujours dans le cadre d’un milieu, souvent support d’un écosystème, où se déroulent de nombreux phénomènes physiques, chimiques et biologiques. L’eau est le constituant presque exclusif de certains de ces milieux (océans, glaciers, rivières, lacs...), alors qu’ailleurs (atmosphère, sols, nappes souterraines...) elle est mêlée ou juxtaposée à d’autres constituants. Dans tous les cas, la spécificité des milieux résulte de l’organisation et de la hiérarchie des phénomènes qui s’y déroulent. On sait aujourd’hui que ces milieux sont les phases d’un cycle de l’eau – structure de l’hydrosphère terrestre – animé par l’énergie du Soleil, qu’il contribue à redistribuer à la surface de la Terre. L’existence et le fonctionnement de ce cycle n’ont été clairement établis qu’au XIX^e siècle, en particulier grâce à la pratique du bilan hydrologique, avatar du principe universel de conservation de la matière.

Si l’objet de l’hydrologie est ainsi bien défini, la diversité réelle des objets hydrologiques et des préoccupations sociales qui les concernent ont suscité des approches parcellaires, parfois justifiables, mais souvent préjudiciables à la compréhension globale des phénomènes hydrologiques. À travers l’océanologie (science des océans), la météorologie (science de l’atmosphère), la glaciologie (science des glaciers), la potamologie (science des rivières), la limnologie (science des lacs), l’hydrogéologie (science des eaux souterraines), émiettement auquel se superpose la diversité des approches physiques, chimiques et biologiques, l’hydrologie telle qu’on peut la souhaiter reste à construire. L’hydrologie telle qu’elle est pratiquée aujourd’hui concerne la partie continentale du cycle de l’eau, et s’intéresse essentiellement aux flux d’eau. Nous en examinerons ici quelques aspects, d’autres articles (GLACIOLOGIE, HYDROGÉOLOGIE, LIMNOLOGIE, POTAMOLOGIE...) en abordant d’autres.

Science du cycle de l’eau, l’hydrologie nourrit d’innombrables applications en raison des nombreux rapports qu’entretiennent l’hydrosphère et l’anthroposphère. L’abondance ou la rareté de l’eau déterminent pour une large part, la géographie humaine en témoigne, la localisation des hommes et de leurs activités. L’homme prélève en effet dans les milieux aquatiques l’eau qui lui est nécessaire pour ses besoins domestiques, agricoles et industriels, mais il y prélève également de l’énergie (hydroélectricité), des matériaux (granulats) et de la nourriture (pêche). Les milieux aquatiques sont également abondamment utilisés pour recevoir et évacuer une bonne part des déchets issus des activités humaines, utilisation évidemment susceptible d’entrer en contradiction avec la précédente. L’eau peut enfin se révéler un danger pour les vies et les activités humaines, en particulier à travers les inondations qui accompagnent les fortes crues.

Depuis la plus haute antiquité, de nombreux efforts ont été accomplis pour transformer les conditions hydrologiques, naturelles ou déjà influencées par les efforts – ou les négligences – des générations précédentes. Le stockage, qui permet de modifier la répartition temporelle de l’eau, et le transport, qui permet de modifier sa répartition spatiale, ont été longtemps les seuls moyens des stratégies de modification des conditions hydrologiques; ils en sont encore les principaux. Trop souvent, malheureusement, ces stratégies ont été élaborées en négligeant leurs effects indirects, particulièrement leur impact sur les écosystèmes aquatiques. On peut citer à cet égard l’aménagement du Nil, dont la pièce maîtresse est le haut barrage d’Assouan, qui collectionne les effets indirects négatifs, imprévus ou sous-estimés. S’il permet bien d’irriguer de vastes étendues et de produire de l’électricité, le haut barrage d’Assouan a entraîné, en aval, l’abaissement du niveau des nappes phréatiques, une progression des intrusions salines dans le delta du Nil, la régression des pêcheries (y compris en Méditerranée occidentale) et, en amont, le remplissage accéléré du réservoir de retenue par les limons, qui ne fertilisent donc plus les terres irriguées, ainsi que la diffusion de la bilharziose.

Aujourd’hui, à côté du stockage et du transport, l’épuration des eaux constitue un nouvel élément des stratégies d’aménagement qui, s’il ne permet pas de résoudre tous les problèmes, y introduit explicitement une nouvelle dimension, celle de la qualité.

Au-delà des aménagements hydrauliques, toutes les transformations de l’espace (défrichement, urbanisation) et la plupart des pratiques humaines ont également des répercussions hydrologiques souvent imprévues, quelquefois lointaines, parfois douloureuses. Que l’on pense, par exemple, aux pluies acides dues à l’émission de rejets gazeux d’oxydes d’azote et de soufre transportés sur de très longues distances avec l’humidité atmosphérique, et qui provoquent d’importants désordres biologiques dans les lacs et les forêts.

La maîtrise sociale de l’eau n’est pas de la compétence de l’hydrologue, mais des gestionnaires de l’eau, qui ont le plus grand besoin des concepts et des connaissances hydrologiques pour résoudre les problèmes qui leur sont posés. La tâche fondamentale de l’hydrologue, dans l’optique de la gestion des eaux, est, selon Vit Klemeš, de fournir des données sur la répartition dans le temps et dans l’espace des eaux qu’il est possible de mobiliser, c’est-à-dire de redistribuer dans le temps et dans l’espace par des ouvrages tels que barrages, canaux, puits, canalisations, pompes... Il faut ajouter à la notion de répartition des eaux celle de leurs propriétés physiques et de leur composition chimique. Signalons de plus que rien n’interdit à l’hydrologue de fournir ces données sous une forme élaborée, celle de modèle mathématique de bassin ou de processus stochastique par exemple. Mais il faut bien se pénétrer du fait que ces données, pour indispensables qu’elles soient, ne sauraient suffire pour élaborer des réponses aux questions relatives à l’aménagement et à la gestion des eaux. Une eau naturelle n’est pas a priori une ressource. Elle le devient, à la suite d’un choix de nature politique, grâce à la mise en œuvre d’un véritable processus de production.

Dans ce contexte, l’intégration des différentes facettes de l’hydrologie n’est donc pas seulement une nécessité théorique, mais également une urgence pratique.

1. Principales étapes de l’hydrologie

Des fondements au développement

Le concept du «cycle de l’eau» paraît avoir été entrevu par Homère et par plusieurs philosophes grecs (Thalès de Milet, Platon, Aristote) et latins (Lucrèce, Sénèque, Pline), mais les conceptions mythiques de cette période « spéculative» ne pouvaient aboutir à un schéma rationnel; Vitruve, qui vivait à Rome à l’aube de l’ère chrétienne, fut le premier à soutenir que les eaux souterraines provenaient, en majeure partie, de la pluie et de la neige infiltrées dans le sol.

Il est pourtant probable que, dès ces temps reculés, les Anciens avaient acquis de bonnes connaissances empiriques sur l’hydrologie, au cours de la construction et de l’exploitation d’ouvrages hydrauliques admirables, comme les réseaux d’irrigation de Mésopotamie et d’Égypte, les puits d’Arabie et les kanats de Perse, les aqueducs de Rome et de l’Indus, les ouvrages de protection contre les crues réalisés par les premières dynasties chinoises, etc.

Il faudra attendre la Renaissance (entre 1400 et 1600 environ) pour que les concepts purement philosophiques cèdent la place à des recherches fondées sur l’observation objective des phénomènes hydrologiques. Léonard de Vinci (1452-1519) s’insurge contre les affirmations d’Aristote. Dans son Discours admirable de la nature des eaux et fontaines tant naturelles qu’artificielles (Paris, 1580), Bernard Palissy donne une interprétation correcte du cycle de l’eau, et tout spécialement de l’alimentation des sources par les pluies.

Mais c’est au cours du XVII^e siècle que sont effectuées les premières mesures hydrométéorologiques, prémices de l’hydrologie moderne. Pierre Perrault (1611-1680) réalise quelques mesures de précipitations, d’évaporation et de perméabilité dans le bassin de la Seine (De l’origine des fontaines , Paris, 1674), tandis qu’Edme Mariotte (1620 env.-1684) procède à quelques jaugeages de ce fleuve à Paris par la méthode des flotteurs. En Italie, alors que la géologie est encore dans l’enfance, Gian Domenico (Jean Dominique) Cassini (1625-1712), Bernardino Ramazzini (1633-1714) et Antonio Vallisnieri (1661-1730) sont les pionniers de l’étude expérimentale des puits artésiens.

Si, dès lors, les premiers fondements de la science hydrologique sont acquis, son développement est freiné par l’insuffisance des sciences fondamentales: physique, mécanique des fluides, météorologie. Par bonheur, au XVIII^e siècle, l’hydraulique théorique et expérimentale progresse; le principe de d’Alembert, le théorème de Bernoulli, la formule de Chézy datent de cette époque, ainsi que le tube de Pitot et le moulinet de Woltman. Désormais, les études d’hydrologie pourront être poursuivies sur une base quantitative.

De ce fait, au cours du XIX^e siècle, l’hydrologie se modernise. Dérivant des travaux de Gotthilf Hagen (1839) et de Jean-Louis Marie Poiseuille «sur le mouvement des liquides dans les tubes de très-petits diamètres» (1840), la loi de Darcy sur l’écoulement des eaux souterraines est publiée en 1856 et la formule de Dupuit-Thiem donnant le débit des puits, en 1863; peu auparavant, William Smith (1769-1839) avait appliqué pour la première fois les connaissances géologiques à la recherche des eaux souterraines. On assiste au développement de l’hydrologie de surface et surtout de l’hydrométrie, jadis délaissées au profit de l’art de découvrir les sources: Andrew Atkinson Humphreys et Henry Larcom Abbot mesurent les débits du Mississippi (1851-1860); le premier jaugeage international du Rhin est exécuté en novembre 1867 à Bâle.

Entre 1900 et 1930, l’hydrologie générale, s’appuyant sur les progrès de l’«hydraulique des coefficients», suscite de nombreux travaux; mais ceux-ci, suivant les errements des sciences de la Terre, procèdent d’un grand empirisme; une foule de chercheurs et d’ingénieurs proposent, dans les domaines les plus variés, des centaines de formules synthétisant des résultats de mesures particulières, mais généralement sans aucun souci de représenter le mécanisme physique des phénomènes. Pour leur application à un problème déterminé, l’ingénieur est souvent embarrassé pour choisir la formule adéquate ainsi que les paramètres et les coefficients que comporte celle-ci, alors que les applications pratiques se multiplient et exigent la rationalisation des techniques de l’hydrologue.

La rationalisation

De ce renouveau d’intérêt témoignent, de 1930 à 1950, d’importants travaux orientés vers l’analyse rationnelle des phénomènes. En 1932, L. K. Sherman propose la méthode de l’«hydrogramme unitaire» pour la prédétermination de l’hydrogramme consécutif à une averse donnée. En 1935, Charles Vernon Theis révolutionne la théorie des puits en étudiant leur comportement en régime non permanent. Vers 1940, Robert Gibrat, Émile Gumbel et de nombreux statisticiens montrent la fécondité des méthodes de l’analyse fréquentielle pour la prédétermination des crues extrêmes. L’étude de l’évaporation est renouvelée par l’utilisation des bilans de rayonnement et des concepts de diffusion turbulente dérivés de la mécanique des fluides.

2. Le cycle de l’eau

Sous sa forme qualitative élémentaire, la description du cycle de l’eau est connue de tous. L’évaporation de l’eau sur les océans et les terres émergées alimente en vapeur les basses couches de l’atmosphère; sous l’effet de la diffusion et de la convection turbulentes, cette vapeur s’élève et atteint éventuellement une altitude suffisante pour former, par condensation, des nuages. Au gré des vents, les systèmes nuageux se déplacent, souvent sur de longues distances, tantôt se renforçant, tantôt s’évanouissant en cours de route. Leur disparition totale ou partielle peut se produire soit par évaporation dans l’air environnant des fines gouttelettes qui les composent, soit par le processus complexe qui déclenche et entretient les précipitations ; celles-ci tombent tant sur les mers – qui couvrent près des trois quarts de la surface de la Terre – que sur les continents.

La quantité d’eau ainsi apportée par la pluie et la neige sur les terres peut, suivant le cas, en tout ou partie: être interceptée par la couverture végétale et s’évaporer à nouveau sans atteindre le sol; ruisseler d’abord à la surface de ce dernier et ensuite dans les multiples ramifications du réseau hydrographique jusqu’à la mer; s’infiltrer dans le sol, dont elle augmente d’abord l’humidité, alimentant ensuite les nappes souterraines.

Sous l’action de l’évaporation, une partie de l’eau ruisselant sur le sol et dans le réseau hydrographique retourne à l’atmosphère durant sa course vers la mer; l’eau interceptée ou transpirée par les végétaux forme une part importante de l’évapotranspiration globale d’une région. L’eau infiltrée et temporairement accumulée dans les aquifères revient, après un plus ou moins long délai, dans le réseau de surface par l’intermédiaire de sources ou de résurgences diffuses inégalement réparties le long du lit des cours d’eau.

Ainsi, le cycle hydrologique met en jeu divers processus bien individualisés – évaporation, précipitation, interception, transpiration (des végétaux), infiltration, percolation, stockage dans les aquifères, ruissellement – qui constituent les principaux chapitres de l’hydrologie.

Bilan hydrologique mondial

Abordons maintenant le bilan hydrologique du globe terrestre dans son ensemble, c’est-à-dire celui du cycle de l’eau.

Les stocks

Le tableau 1 donne la valeur des différents stocks. On remarquera que les océans – eaux salées – représentent plus de 97 p. 100 des eaux terrestres; uniformément répartis sur le globe, leur épaisseur moyenne serait de 2 640 mètres. L’eau douce ne représente que 2,6 p. 100 des eaux terrestres, et les rivières, qui sont abondamment exploitées pour l’alimentation en eau et l’évacuation des déchets, ne représentent que 0,003 p. 100 de cette eau douce.

La valeur de ces stocks hydriques varie dans l’espace et dans le temps. Ainsi, on admet couramment que l’humidité atmosphérique (dont les neuf dixièmes sont contenus dans les cinq premiers kilomètres de l’atmosphère) représenterait, si elle était répartie uniformément sur la surface du globe, une «hauteur d’eau condensable» de l’ordre de 25 millimètres d’épaisseur, mais la hauteur d’eau condensable peut atteindre, exceptionnellement, 150 millimètres au mois de juillet en Floride et s’abaisser à quelques millimètres en février dans l’Extrême-Nord sibérien.

Les flux

Les différentes phases du cycle de l’eau échangent constamment de la matière par précipitation, évaporation, infiltration, etc. Le tableau 2 présente la précipitation et l’évaporation moyennes sur les continents et les océans, estimées pour l’année 1973.

La rotation du stock d’humidité de l’atmosphère est relativement rapide, et des volumes d’eau représentant environ trente fois la hauteur d’eau condensable moyenne y transitent au cours d’une année. Si la hauteur moyenne des précipitations sur l’ensemble du globe est de l’ordre de 980 millimètres par an, il tombe 11 mètres d’eau par an en moyenne à Tcherrapoundji, sur les contreforts de l’Himalaya, tandis qu’au Sahara certaines années n’apportent aucune pluie.

L’évaporation varie également dans des proportions considérables. Des valeurs dépassant 10 millimètres par jour ont été mesurées sur les nappes d’eau peu profondes des zones arides en période sèche, tandis que les champs de neige de l’Alaska évaporent en hiver moins d’un millimètre par jour.

3. Les précipitations

Les précipitations sont constituées des chutes de pluie, de grêle ou de neige provenant de la condensation, dans des conditions météorologiques particulières, de la vapeur d’eau atmosphérique. Elles constituent l’unique «entrée» des principaux systèmes hydrologiques continentaux que sont les bassins versants.

Les précipitations se produisent de manière intermittente et finalement assez rarement. La durée moyenne annuelle des précipitations varie, en France, de 400 à 1 400 heures, soit 10 p. 100 environ du temps. Formées d’éléments discrets (gouttes, grêlons, flocons...) dont les paramètres n’intéressent guère l’hydrologue, les précipitations sont mesurées par leur hauteur rapportée à un intervalle de temps. Cette hauteur est définie comme l’épaisseur de la lame d’eau qui s’accumulerait sur une surface horizontale pendant cet intervalle de temps si toutes les précipitations, éventuellement après fonte, y étaient immobilisées. L’instrument de mesure de base est le pluviomètre. Il s’agit d’un récipient ayant la forme d’un seau, fixé sur un support, et dont l’ouverture, placée horizontalement et limitée par une bague à bord effilé, a une surface parfaitement définie (400 cm² selon la norme française). Un dispositif interne en forme d’entonnoir permet de limiter les pertes par évaporation. La mesure proprement dite est réalisée grâce à une éprouvette convenablement graduée dans laquelle l’eau recueillie par le pluviomètre est versée (fig. 1). Malgré les apparences, cette mesure est délicate car le pluviomètre provoque dans son environnement des perturbations aérodynamiques qui affectent le phénomène mesuré. Sans la surmonter totalement, on limite cette difficulté en définissant des normes d’installation des appareils (hauteur, environnement) qui permettent en tout cas d’obtenir des mesures comparables. Le pluviomètre nécessite l’intervention d’un observateur et ne convient donc que pour des observations portant sur des durées de quelques heures. L’essentiel de l’information pluviométrique est recueillie de cette façon selon un pas de temps journalier, les observations étant réalisées le matin.

Si l’on s’intéresse à des durées de temps plus courtes, ou à des sites éloignés et/ou peu accessibles, il faut utiliser un appareil automatique, le pluviographe, qui enregistre la hauteur cumulée des précipitations en fonction du temps sur une bande de papier ou sur un support magnétique.

Le rapport de la hauteur d’eau tombée pendant une période à la durée de cette période est l’intensité moyenne de la pluie pour cette période (fig. 2). Pour une station de mesure et une durée données, les observations disponibles constituent un échantillon statistique à partir duquel on peut, empiriquement ou après ajustement d’une distribution théorique appropriée, attribuer une probabilité de dépassement à toute valeur de l’intensité moyenne. L’intensité moyenne susceptible d’être dépassée avec une probabilité donnée, sur un intervalle de temps donné, est une fonction décroissante de la durée de cet intervalle. L’information statistique ainsi recueillie est généralement présentée sous la forme de courbes fréquence-intensité-durée, la fréquence étant souvent traduite en période de retour (inverse de la probabilité du dépassement), exprimée en années.

Les précipitations sont liées à des phénomènes météorologiques dont la persistance, dans le cadre des variations saisonnières, n’excède pas quelques jours. On pourra donc considérer, et les tests statistiques le confirment, que les précipitations annuelles, mensuelles, voire décadaires, sont indépendantes.

On admet généralement que les pluies annuelles sont distribuées selon une loi normale. On peut cependant constater pour certaines stations, par exemple celles de climat méditerranéen, une légère asymétrie, positive, des distributions de pluies annuelles. La moyenne de la distribution, appelée module pluviométrique, est la principale norme hydrologique permettant de se faire une première idée du potentiel hydrique d’une station et de la région qui peut lui être associée. Il est nécessaire de disposer d’une trentaine d’années de mesures pour estimer correctement un module pluviométrique. On peut cependant se poser légitimement des questions sur la stationnarité des séries pluviométriques annuelles et, partant, sur la signification du module pluviométrique. C’est ainsi que la plupart des stations du Sahel, pour lesquelles on dispose généralement de mesures depuis les années vingt, présentent depuis le début des années soixante-dix des pluviométries inférieures au module pluviométrique calculé à partir des précipitations antérieures. Une telle suite est statistiquement impossible (sa probabilité est de l’ordre de 10^-6) dans le cadre d’un modèle stationnaire. Si l’on ne renonce pas à l’hypothèse d’indépendance, il faut plutôt voir là les effets d’une évolution climatique, dans laquelle l’action de l’homme a peut-être une place. Les séries pluviométriques pourraient alors être stationnaires par morceaux, mais on est alors conduit à relativiser la signification du module pluviométrique et, au-delà, des autres paramètres hydrométéorologiques.

Une perturbation atmosphérique pluviogène s’étend sur un domaine dont la surface peut aller de quelques kilomètres carrés à quelques dizaines de milliers de kilomètres carrés. À un instant donné, il ne pleut cependant pas partout dans ce domaine, et, là où il pleut, l’intensité de la pluie est très variable. L’imagerie radar permet de mesurer la complexité des champs pluviométriques (fig. 3). La surface où il pleut à un instant donné est extraordinairement morcelée et ses contours particulièrement complexes. Les appareils de mesure fixes – pluviomètres et pluviographes –, organisés en réseau (fig. 4), permettent d’échantillonner les précipitations cumulées pendant une fraction ou la totalité de l’épisode. On retrouve là une grande variabilité, d’autant plus grande que l’intervalle de temps considéré est court. Il faut noter que le rapport d’échantillonnage est extrêmement faible puisque les réseaux considérés comme relativement denses comportent de l’ordre d’un pluviomètre (400 cm²) pour 100 kilomètres carrés. Le passage de mesures ponctuelles à une estimation spatiale, souvent nécessaire en hydrologie et que l’on retrouvera au niveau de l’estimation de l’évapotranspiration, est délicat. Les méthodes les plus simples font appel à la notion d’abattement (rapport de la lame d’eau moyenne sur une surface à la hauteur ponctuelle maximale), qui est traitée en termes probabilistes. De nombreuses méthodes d’interpolation ont également été définies et certaines d’entre elles, comme le krigeage, qui s’appuie sur la théorie des variables régionalisées, permettent d’associer un intervalle de confiance à l’estimation de la lame d’eau moyenne.

4. L’évapotranspiration

L’évapotranspiration est la somme de la transpiration du couvert végétal (à travers les stomates des plantes) et de l’évaporation des sols et des surfaces d’eau libre. On désigne comme évapotranspiration réelle (ETR) la valeur de ce flux à un instant donné ou de sa moyenne sur une période donnée, pour une station donnée. Lorsque la disponibilité en eau n’est pas limitative, ce flux tend vers une limite appelée évapotranspiration potentielle (ETP). Ce dernier concept, essentiellement théorique, caractérise une certaine demande en eau exercée par le milieu.

Bien que le terme d’évapotranspiration réelle soit toujours très important dans le bilan en eau, il est souvent traité cavalièrement, sans doute en raison des difficultés liées à son estimation. Il n’est en effet pas possible de le mesurer directement.

L’évaluation de l’évapotranspiration d’une surface passe par l’évaluation de son bilan d’énergie. Une surface reçoit du Soleil et de l’atmosphère des radiations de diverses longueurs d’onde, dont une partie est réfléchie. Elle-même émet de l’énergie sous forme radiative selon sa température. Le solde radiatif modifie la température de la surface émissive, alimente un flux de chaleur sensible vers le sol et vers l’atmosphère et fournit la chaleur latente nécessaire aux processus d’évapotranspiration (on sait en effet que l’évaporation d’un gramme d’eau nécessite de l’ordre de 2 500 joules à la température ambiante). La chaleur sensible et la vapeur d’eau sont évacuées dans l’atmosphère de façons similaires, selon un processus de diffusion turbulente. Les limites du processus évaporatoire sont donc liées à la disponibilité en eau et en énergie et aux capacités d’évacuation de la vapeur d’eau dans l’atmosphère.

L’établissement du bilan énergétique permettant d’accéder à l’évapotranspiration ne pose pas de problèmes trop délicats, en particulier pour des durées de l’ordre de l’heure, pour lesquelles on peut raisonnablement postuler des conditions stationnaires, à condition de disposer des données nécessaires qui sont, hélas! nombreuses et souvent délicates et/ou coûteuses à recueillir. Il s’agit essentiellement des éléments du bilan radiatif et des profils dans l’atmosphère, au voisinage de la surface étudiée, de la température, de l’humidité et de la vitesse du vent. C’est sur ces solides bases physiques qu’ont pu être établies certaines formules, comme la célèbre formule de Penman, qui permet d’estimer l’ETP journalière, dont les deux termes de rayonnement et d’advection sont naturellement reliés aux deux moteurs du processus évapotranspiratoire.

D’autres formules se contentent de données plus rustiques, comme celle des évaporomètres sous abri (évaporomètre Piche), des bacs d’évaporation ou de la mesure de la durée d’insolation, mais elles exigent le calage de coefficients qui sont finalement des coefficients de régression dont la signification physique est incertaine. Des centaines de telles formules existent. Leur intérêt pratique est indéniable, mais elles doivent être utilisées avec précaution sans oublier ni les hypothèses, parfois fort restrictives, qui les sous-tendent, ni le contexte géoclimatique parfois fort limité dans lequel elles ont été établies. Ces précautions sont souvent oubliées: la formule de Thornthwaite, qui estime fort correctement l’ETP mensuelle à partir de la température de l’air et de la durée d’insolation pour un gazon anglais , a connu une brillante carrière sous tous les climats!

5. Le bassin versant

Si l’on considère une section droite d’un cours d’eau, on peut lui associer un bassin versant, lieu géométrique des points de l’espace géographique où les précipitations sont susceptibles de contribuer au débit observé dans cette section. On définit aisément le bassin versant topographique limité par une ligne de partage des eaux, mais celui-ci peut différer du bassin versant réel à cause des circulations souterraines qui drainent parfois des eaux extérieures au bassin topographique ou, au contraire, drainent des eaux du bassin topographique hors de ce dernier. Il se peut d’ailleurs, dans le cas de nappes souterraines situées à cheval sur deux ou plusieurs bassins topographiques, que les limites du bassin réel fluctuent au cours du temps. Malgré ces difficultés, le bassin versant demeure l’objet fondamental de l’hydrologie continentale, celui qui transforme la pluie en débit, ces deux flux possédant d’ailleurs une série de propriétés physico-chimiques qui subissent elles aussi une transformation lors de leur passage sur et/ou à travers le bassin versant.

Le bassin versant est un objet complexe dont l’ensemble des caractéristiques (géométriques, géologiques, physiographiques, humaines, etc.) joueront un rôle non seulement dans le processus de transformation de la pluie en débit mais aussi, en amont et pour certaines d’entre elles (altitude, exposition...), dans le processus de formation de la pluie. Il faut noter à la surface du bassin versant l’existence d’un système de singularités, le réseau de drainage, arborescence dont l’exutoire du bassin constitue la racine et dont les rivières et les ruisseaux constituent les branches. Ce réseau est plus ou moins développé selon les circonstances et peut même exceptionnellement se confondre avec le bassin lorsque celui-ci ruisselle en tout point. La vitesse d’écoulement dans ce réseau, qui est de l’ordre du kilomètre par heure, est infiniment plus grande que celle de l’écoulement souterrain, qui est plutôt de l’ordre du mètre par jour.

Il ne manque pas dans la littérature scientifique de paramètres quantifiés destinés à mesurer telle ou telle caractéristique des bassins versants. Nous citerons par exemple l’indice de compacité (dit de Gravelius), rapport du périmètre du bassin au périmètre du cercle de même surface, destiné à caractériser la forme, allongée ou ramassée, du bassin. Ces quantifications restent le plus souvent un exercice de style car les paramètres correspondants ne trouvent pas leur place dans les modèles pluie-débit, dont les paramètres sont la plupart du temps des coefficients issus d’une régression. Les concepts de la géométrie fractale, qui connaissent quelques applications dans ce domaine, sont susceptibles d’asseoir la modélisation des bassins versants sur des paramètres dont la signification physique est indiscutable (fig. 5).

Le bassin versant est le siège de deux phénomènes, intimement liés mais qu’il convient de distinguer: la propagation des ondes hydrauliques provoquées par les pluies et le transport de l’eau qu’elles apportent. Cette distinction n’a rien de byzantin. Si on se préoccupe de reconstituer les débits d’eau à l’exutoire d’un bassin versant à partir des hauteurs de pluie, et cela a été longtemps le souci principal des hydrologues, il suffit d’étudier la propagation à travers le bassin, qui agit alors comme un filtre, de l’onde hydraulique provoquée par la pluie. Il n’est alors pas nécessaire de connaître le cheminement des molécules d’eau participant au débit. Les lois régissant l’écoulement – équation de diffusivité issue de la loi de Darcy en milieu souterrain, équation de Barré de Saint-Venant en rivière – concernent d’ailleurs les charges et ne permettent pas le suivi des particules fluides. Mais si l’on se préoccupe de reconstituer le débit et certaines de ses caractéristiques physico-chimiques (concentrations en nitrates, par exemple, qui suscitent bien des inquiétudes), déterminer le cheminement des molécules d’eau à travers le bassin devient une nécessité supplémentaire, car ce cheminement déterminera l’histoire géochimique de l’eau et, partant, ses caractéristiques physico-chimiques.

Une telle séparation de l’hydrogramme (courbe du débit en fonction du temps) est possible expérimentalement grâce aux techniques utilisant les isotopes naturels de l’oxygène (¹⁸O) et de l’hydrogène (²H ou deutérium, ³H ou tritium), qui réalisent un marquage naturel de la molécule d’eau. Ces techniques mettent généralement en évidence une participation des eaux d’origine souterraine au débit plus importante que celle qui est traditionnellement déterminée par des manipulations purement formelles sur l’hydrogramme (fig. 6). Ce constat expérimental ne met cependant pas en cause l’existence du phénomène de ruissellement superficiel, qui prend naissance localement dès que l’intensité de la pluie est supérieure à la capacité d’infiltration du sol et qui est nécessairement associé aux crues les plus importantes.

Le premier modèle hydrologique moderne est certainement celui de l’hydrogramme unitaire. Sans qu’il soit possible de le développer ici, nous signalerons simplement qu’il suppose que la transformation permettant de passer de la pluie nette, celle qui ruisselle, au débit est une transformation linéaire. L’hydrogramme unitaire est la réponse en débit du bassin à une averse unitaire, apportant une unité de volume d’eau uniformément répartie sur le bassin pendant une durée suffisamment petite devant le temps de concentration du bassin (maximum de la durée nécessaire à une goutte d’eau pour parcourir le chemin hydrologique entre un point du bassin et l’exutoire de ce dernier).

On peut identifier l’hydrogramme unitaire, qui apparaît alors comme une fonction de transfert, à partir d’un couple hyétogramme-hydrogramme, par déconvolution (le hyétogramme est la courbe représentant l’intensité de la pluie en fonction du temps). Cette fonction de transfert permet alors, par convolution, de calculer l’hydrogramme afférent à un hyétogramme donné. La reconnaissance, qui est presque une découverte, de l’extrême variabilité des champs pluviométriques mais aussi de l’évapotranspiration et des caractéristiques des bassins, de même que l’approfondissement des études concernant le transport de l’eau dans les bassins ont passablement lézardé l’édifice de l’hydrogramme unitaire et, en tout cas, rogné ses prétentions théoriques. Il apparaît davantage aujourd’hui comme un modèle conceptuel, construit à partir d’une image de la réalité plutôt qu’à partir de bases physiques indiscutables.

Bilan hydrologique d’un bassin versant

Sous sa forme la plus générale et pour une période déterminée (mois, année), ce bilan s’exprime, en volumes, par une équation de continuité de la forme:

dans laquelle E représente le total des apports hydriques de toute sorte au système considéré, S l’ensemble des volumes d’eau sortant du système, R la variation des stocks d’eau existant dans ce dernier entre le début et la fin de la période considérée.

Pour concrétiser ces notions, considérons d’abord le cas simple du bassin versant d’une rivière au droit d’une station de mesure ; pour simplifier, supposons qu’il n’y a ni fuite ni apport d’eau à travers les frontières de ce bassin (la ligne de partage des eaux). Son bilan d’écoulement peut être schématisé comme dans le tableau 3 (pour une période d’une année par exemple).

On voit qu’ici le terme E de l’équation de continuité se limite à l’apport des précipitations P, tandis que le terme S est la somme des volumes Q écoulés au droit de la station de jaugeage et des quantités d’eau D évaporées par les nappes d’eau, les sols et la couverture végétale du bassin. Le terme D, calculé sur un nombre d’années assez grand pour que R soit négligeable, s’appelle le déficit d’écoulement du bassin; il présente un grand intérêt pratique du fait que sur de larges régions il varie relativement peu; en Europe occidentale, il oscille entre 400 et 600 millimètres suivant la température moyenne, les précipitations et le degré de continentalité du climat. Connaissant P, on peut donc obtenir une première estimation de Q par la relation: Q = P 漣 D.

6. Les débits des cours d’eau

La série chronologique des débits observés pendant une durée suffisamment longue, en une ou plusieurs sections d’un cours d’eau, constitue l’information hydrologique de base concernant ce cours d’eau. La plupart des pays du monde ont établi sur leur réseau hydrographique des réseaux de mesure, constitués d’un ensemble de stations de jaugeage, pour recueillir cette information. La formation d’un personnel compétent, l’entretien des réseaux, la constitution de banques de données ne sont cependant pas gratuits et leur rentabilité n’est pas toujours évidente aux yeux d’administrations souvent soucieuses de rationalisation sous forme d’économies qui risquent d’affecter la quantité, la continuité et la qualité de l’information recueillie. On ne dira jamais assez la valeur de cette information, indispensable à tout projet d’aménagement et sans laquelle les développements les plus élaborés de l’hydrologie moderne ne seraient que bavardages.

Mesure des débits

L’hydrogramme, courbe des débits en fonction du temps, Q = f (t ), à une station de jaugeage, se déduit, en général, de la courbe des hauteurs d’eau H(t ) au droit de cette station; ces hauteurs d’eau sont lues par un observateur sur une échelle limnimétrique qui indique l’altitude du plan d’eau par rapport à un repère fixe, ou enregistrées d’une façon continue par un limnigraphe ou même transmises à un poste central par un système de télémesure. On déduit de la courbe des hauteurs d’eau H(t ) ainsi relevée celle des débits Q(t ), au moyen de la courbe de tarage Q(H) de la station (fig. 7); celle-ci est établie expérimentalement en déterminant (en principe une fois pour toutes), par une série de jaugeages, les débits Q¹, Q², ..., Qⁿ traversant la section de mesure de la station pour des cotes du plan d’eau H¹, H², ..., Hⁿ , lues à son échelle limnimétrique et également réparties entre les plus hautes et les plus basses eaux.

Ces jaugeages sont, le plus souvent, effectués par intégration du champ des vitesses de l’écoulement dans une section droite du cours d’eau, judicieusement choisie sur le site de la station. Les vitesses de l’eau en divers points de cette section sont mesurées au moyen d’un moulinet hydrométrique , essentiellement constitué par une petite hélice mise en rotation par l’écoulement (fig. 8); une courbe d’étalonnage permet d’obtenir la vitesse locale V de l’eau en fonction de la vitesse de rotation n du moulinet; si d S est l’élément de la section droite siège de la vitesse V, le débit Q dans la section droite de superficie S est la somme des débits élémentaires, tels que Vd S; il est donné par l’intégrale double:

La méthode ci-dessus tend aujourd’hui à être remplacée, pour le jaugeage des petits et moyens cours d’eau, par les méthodes dites «de dilution ». Celles-ci consistent essentiellement à injecter dans une section du cours d’eau un très petit débit q , mesuré avec précision, d’une solution aqueuse d’un sel (bichromate de soude) de concentration C; dans une section située suffisamment en aval de la section d’injection pour que la solution saline soit bien mélangée à l’écoulement, on prélève des échantillons de l’eau de la rivière et on titre la teneur en «sel injecté» de ces derniers. Si c est cette concentration, il est facile de montrer que le débit Q cherché a pour expression:

Pour les ruisseaux, et surtout pour les torrents de montagne, on utilise parfois des stations dont le dispositif de mesure est constitué par un déversoir (en mince paroi ou à large seuil) ou par un jaugeur à ressaut; le débit est alors calculé à partir des «hauteurs d’eau» par les formules de l’hydraulique, et il n’est pas nécessaire de procéder à des jaugeages pour «tarer» la station.

Présentation des données statistiques relatives aux débits

Les relevés de débit effectués à une station de jaugeage pendant de nombreuses années forment un ensemble assez peu maniable de chiffres et de graphiques; il est indispensable de résumer et de coordonner cette multitude d’observations en quelques éléments synthétiques, en nombre aussi faible que possible mais pourtant suffisants pour caractériser la station, aux différents points de vue qui intéressent l’hydrologue ou l’ingénieur.

À cet effet, les hydrologues ont depuis longtemps établi des tableaux et des graphiques chronologiques donnant les valeurs des débits journaliers, mensuels, saisonniers, annuels, etc., dans l’ordre où ils se sont succédé dans une période calendaire déterminée. Pour condenser les informations données par ce mode de présentation, on a très tôt établi la moyenne des débits annuels, mensuels ou journaliers, afférents à une série d’années (tabl. 4); les chiffres ainsi obtenus ont été considérés comme les débits d’une «année moyenne» fictive; mais celle-ci n’ayant jamais existé réellement, ce concept peut conduire, en pratique, à de graves erreurs. Le débit relatif à un même jour ou à un même mois varie, en effet, largement d’une année à l’autre, et le mode de calcul des débits de l’année moyenne conduit à une régularisation artificielle du régime par compensation des années sèches et humides.

La «moyenne» ne permettant de caractériser que la valeur centrale ou dominante d’une série, on lui associe le plus souvent un paramètre mesurant la dispersion (ou fluctuation) des diverses observations autour de la valeur centrale; en effet, dans beaucoup d’applications, la connaissance des débits extrêmes (crues et étiages) a au moins autant d’importance que celle des débits moyens.

La dispersion d’une série d’observations peut être caractérisée très brièvement par son écart type ou par son coefficient de variation. Pour plus de détails, l’hydrologue préférera souvent aux courbes chronologiques des courbes monotones telles que la courbe de distribution des fréquences des débits ou la courbe des fréquences cumulées. Cette dernière n’est autre que la traditionnelle courbe des débits classés (fig. 9). Chaque point de cette courbe donne, en ordonnée, la valeur du débit qui a été atteint ou dépassé pendant le nombre de jours figurant en abscisse. Les points remarquables de cette courbe définissent les débits caractéristiques du cours d’eau à la station considérée; ainsi, les débits caractéristiques de un, trois, six ou neuf mois (DC1, DC3, DC6, DC9) sont les débits atteints ou dépassés respectivement un mois, trois mois, six mois ou neuf mois par an.

7. Les crues

Caractéristiques et classification

Parmi tous les phénomèmes hydrométéorologiques, les grandes crues retiennent tout particulièrement l’attention du public en raison des modifications spectaculaires qu’elles apportent aux paysages riverains et de leurs effets destructeurs parfois considérables. Aussi le problème le plus souvent posé à l’hydrologue est-il celui de la prédétermination de la crue maximale à craindre en un point d’un cours d’eau; le débouché des ponts, les dimensions des évacuateurs de crues d’un barrage, la hauteur des digues de protection contre les inondations d’une zone urbaine ou rurale sont en effet essentiellement déterminés par le débit maximal probable de la crue à laquelle ces ouvrages devront faire face, compte tenu de certaines considérations d’optimalisation économique. D’où les nombreuses études effectuées, notamment au cours des dernières décennies, par les hydrologues, les statisticiens, les ingénieurs et les économistes.

Les maximums instantanés de débit ou de hauteur atteints par une crue ne suffisent pas à caractériser celle-ci; la durée de la crue et de ses principales phases (temps de montée, durée de la décrue, etc.), le volume total écoulé, et le tracé de l’hydrogramme (relevé par un limnigraphe ou reconstitué à partir d’observations fréquentes) sont indispensables pour l’établissement de la plupart des projets de protection contre les inondations. Malheureusement, lorsqu’il s’agit de phénomènes aussi exceptionnels et aussi destructeurs que les crues catastrophiques, il est assez rare que l’on dispose de données très précises.

Eu égard aux causes qui les engendrent, les crues sont généralement groupées en trois grandes classes: crues d’averses, crues de fonte de neige et crues d’embâcle ou de débâcle de glace. Seules les premières seront ici évoquées.

Le plus souvent, les grandes crues ont pour origine des averses exceptionnelles par leur intensité, leur extension et leur durée. Sur l’ensemble d’un grand bassin, celles-ci semblent se reproduire à intervalles plus ou moins éloignés suivant des modalités à peu près analogues; cette similitude, parfois grossière, des répartitions pluviométriques s’explique par le tracé habituel des trajectoires des fortes perturbations météorologiques, ainsi que par la position géographique et le relief des bassins considérés. En dehors de ces pluies générales, des averses orageuses courtes, violentes et très localisées, peuvent produire sur les petits bassins, notamment en montagne, des crues de très faible durée capables de provoquer de gros dégâts en raison de leur fort débit de pointe. Si l’on remarque qu’une intensité de précipitation de 1 millimètre par minute fournit un débit d’eau pluviale de 16,7 m³ 練 s^-1 練 km^-2, on comprend que l’on ait pu observer, sur certains petits bassins méditerranéens d’une dizaine de kilomètres carrés, des débits spécifiques de 20 à 30 m³ 練 s^-1 練 km^-2 lors du maximum de crues de courte durée.

L’étude du processus de transformation des précipitations en débits montre d’ailleurs que des averses apportant une même hauteur totale de pluie donnent des débits de pointe très différents: la topographie, les dimensions (et la forme) du bassin versant, le tracé du réseau hydrographique conditionnent le temps de concentration dudit bassin; la température, l’état de surface (sol gelé ou latérisé, nature et extension de la couverture végétale) et la perméabilité du sol, la saison, etc., déterminent les «pertes» de l’averse, c’est-à-dire la fraction de celle-ci qui est soustraite à l’écoulement immédiat; l’intensité et la distribution spatiale et temporelle des précipitations influent notablement sur la forme de l’hydrogramme.

Méthodes de prédétermination

On peut classer les méthodes utilisées par les hydrologues et les ingénieurs pour prédéterminer les débits de crue en méthodes dites empiriques, en méthodes statistiques, fondées sur l’analyse de la fréquence des crues observées, et aussi en méthodes hydrométéorologiques.

La plus ancienne des méthodes empiriques est celle dite de la « plus grande crue historique». Le débit de celle-ci ayant été estimé à une certaine valeur d’après les observations disponibles, on admet que celui de la crue maximale à craindre est égal à cette valeur multipliée par un coefficient de sécurité dont l’estimation demeure assez subjective.

Dès 1913, Myron L. Fuller a introduit la notion fondamentale de la variation du débit maximal probable q (T) de la crue en fonction de la durée d’observation ou, plus précisément, de la «durée de retour» T de celle-ci (T est l’inverse de la fréquence de non-dépassement observée, laquelle peut être prise comme une estimation de la probabilité correspondante); à ce titre, Fuller peut être considéré comme le promoteur des méthodes statistiques d’analyse fréquentielle .

Dans ces dernières méthodes, la crue annuelle – définie comme le plus fort débit de l’année – est considérée comme une variable aléatoire continue et illimitée dont on étudie la distribution statistique. À cet effet, la série des crues annuelles observées pendant une durée aussi longue que possible – au moins une trentaine d’années – est ajustée sur une loi théorique de distribution appropriée (Gumbel, Fréchet, Pearson III), de façon à interpréter aussi fidèlement que possible les observations du passé; on admet que cette loi est valable pour des probabilités largement inférieures aux fréquences observées et permet donc de calculer, par extrapolation, la valeur du débit de la crue correspondant à une « probabilité de non-dépassement», même très petite.

La figure 10 montre l’application de la méthode aux débits maximaux annuels du Rhin à Rheinfelden ajustés sur la loi de distribution de Fréchet; le «papier à probabilités» utilisé indique, en ordonnée, les débits en mètres cubes par seconde en fonction de leur probabilité de non-dépassement 淋(y ) portée en abscisse.

Les méthodes hydrométéorologiques visent à calculer le débit maximal auquel donnera lieu l’averse la plus dangereuse pouvant tomber sur le bassin considéré, à partir de l’étude du mécanisme de la transformation des pluies en débit (en utilisant par exemple la méthode de l’«hydrogramme unitaire» et la théorie de la propagation des crues).

Le choix de l’averse la plus dangereuse est particulièrement délicat; cette averse est souvent estimée par des méthodes météorologiques de « maximisation» et de «transposition» des averses observées sur des bassins réputés analogues. Le calcul de la probabilité d’occurrence de telles averses et des crues qu’elles engendrent reste encore assez subjectif.

8. Les modèles mathématiques

L’évolution de l’hydrologie au cours des dernières décennies a été marquée par l’introduction de l’informatique. Cette dernière a d’abord permis, et permet toujours, la réalisation rapide, économique et sûre de tâches traditionnelles de collecte, de stockage, d’édition et de traitement des volumineuses données hydrologiques. Mais l’informatique a également permis de mettre en scène et d’animer l’information hydrologique de façon nouvelle grâce à la construction de modèles mathématiques.

Considérons un objet hydrologique; il est très généralement possible de formaliser un modèle mathématique en temps discret de cet objet par une expression du type:

y ^t est un vecteur dont les composantes sont les valeurs prises au temps t par un ensemble de variables endogènes, dites aussi variables

de sortie, telles que débit ou température d’une rivière, niveau d’un lac ou d’un puits. x ^t est un vecteur dont les composantes sont les valeurs prises au temps t par un ensemble de variables exogènes, dites aussi variables d’entrée, telles que hauteurs de précipitation, température de l’air ou vitesse du vent. est un vecteur de paramètres, indépendants du temps, sur la signification desquels nous reviendrons.

La fonction f traduit la nature et la structure du modèle utilisé. Elle est liée, sous la forme où nous l’avons écrite, à un pas de temps et permet, à partir de l’historique des variables exogènes à partir du temps t (x ^t , x ^t-1 , x ^t-2 , ...), de l’historique des variables endogènes à partir du temps t 漣 1 (y ^t-1 , y^t-2 , ...) et des paramètres ( ), de calculer:

Dans un modèle déterministe, y ^t sera considéré comme une estimation au temps t du vecteur des variables endogènes. Ce vecteur estimé y ^t est généralement différent du vecteur observé y ^t en raison de l’imprécision des données et de l’imperfection du modèle, incertitudes qui s’incarnent dans le terme 﨎^t , qui apparaît alors comme une erreur d’estimation.

Dans un modèle stochastique, y ^t sera considéré comme une composante déterministe à laquelle s’ajoute une composante aléatoire 﨎^t .

On distingue souvent les modèles empiriques et les modèles conceptuels. Dans les premiers, on ne se préoccupe pas des processus physiques à l’œuvre dans la production du phénomène étudié. On se contente d’établir une relation entre variables explicatives et variables expliquées. C’est, par exemple, le cas des modèles (stochastiques) autorégressifs d’ordre p , souvent utilisés pour modéliser les débits:

Le débit relatif à une période donnée (y ^t ) est ici exprimé comme une fonction linéaire des débits des p périodes précédentes augmentée d’un terme aléatoire.

Les auteurs de modèles conceptuels fabriquent au contraire une image de l’objet modélisé où les phénomènes physiques ont explicitement leur place. C’est le cas des modèles (déterministes) à réservoirs tels que le modèle de bassin versant représenté sur la figure 11.

Ici, la précipitation et l’évapotranspiration potentielle constituent les variables exogènes, les stocks et les débits constituant les variables endogènes. La précipitation augmente la réserve en eau disponible du réservoir «sol» qui alimente l’évapotranspiration réelle (jusqu’à concurrence de l’évapotranspiration potentielle), l’infiltration et éventuellement le ruissellement. L’eau infiltrée comme l’eau ruisselée passent ensuite dans des réservoirs simulant le transfert souterrain (réservoir «zone non saturée» et réservoir «nappe») et le transfert superficiel (réservoir «surface»). Le débit à l’exutoire du bassin est finalement constitué de vidanges et de débordements des différents réservoirs considérés. Chaque réservoir est caractérisé par un ou plusieurs paramètres de volume et un ou plusieurs paramètres de vidange. Nous détaillerons sur le réservoir «zone non saturée» le fonctionnement d’un tel modèle (fig. 12). Ce réservoir est caractérisé par quatre paramètres (R^M, R⁰, k ^v , k ^h ). Il reçoit le débit d’infiltration Qⁱ produit par le réservoir «sol». Quel que soit le volume R contenu dans ce réservoir (compris entre 0 et R^M, volume maximal), il se vidange avec un débit Q^v vers le réservoir «nappe» selon un processus du premier ordre de constante k ^v :

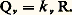
Dès que le volume V est supérieur au volume R⁰ (compris entre 0 et R^M), une seconde vidange, de constante k ^h , est déclenchée, dont le débit Q^h alimentera directement le débit à l’exutoire du bassin:

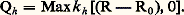
Dès que le volume du réservoir atteint le volume maximal R^M apparaît un débit de débordement Q^d .

L’équation du bilan du réservoir s’écrit alors:

équation qui peut être discrétisée selon un pas de temps adéquat.

Un modèle «agrégé» de bassin versant tel que celui-ci peut devenir «distribué» si son schéma est appliqué à diverses unités spatiales contiguës dont les entrées et les paramètres peuvent alors être diversifiés.

Pour faire «tourner» un modèle, c’est-à-dire l’animer grâce à un programme exécuté par un ordinateur, il est nécessaire d’attribuer une valeur numérique à chacun de ses paramètres. Il est parfois possible, lorsque ces paramètres ont une signification physique, de les mesurer in situ ou, au moins, de les estimer a priori. Cela est rarement le cas, même pour les modèles conceptuels, et les paramètres correspondants doivent être calés en recherchant, par une procédure d’optimisation, le jeu de paramètres minimisant un critère donné. Connaissant les x ^t et les y ^t pour t appartenant à une chronique T, on cherchera par exemple le vecteur minimisant l’expression:

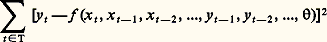
si le critère choisi est la proximité, au sens des moindres carrés, entre valeurs estimées et valeurs observées. Une fois calé, le modèle devra être validé sur une chronique n’ayant pas servi au calage. Il faut cependant être conscient du fait que les paramètres sans signification physique offrent au modélisateur une liberté de manœuvre dont il peut être tenté d’abuser. La plus grande parcimonie devrait donc être de rigueur dans l’introduction de tels paramètres.

Un modèle mathématique est un moyen d’organiser, de vérifier et d’animer l’information hydrologique en vue d’atteindre un objectif de gestion et/ou de connaissance. Parmi ces objectifs, on distingue dans le jargon hydrologique la prévision de la simulation. La première réalise un pronostic concernant la valeur d’une grandeur hydrologique à un moment donné, la seconde fournissant des chroniques vraisemblables mais non datées de telles grandeurs.

Pour un objet hydrologique donné, la gamme des modèles possibles est pratiquement infinie. Le choix d’un modèle et le mode d’estimation de ses paramètres représentent donc toujours un compromis entre l’objectif affiché, souvent ambitieux, et l’information disponible, toujours insuffisante.

• 1614; de hydro- et -logie

Synonymes :

Synonymes :

Synonymes :

n. f. Didac. Science qui traite des eaux, de leurs propriétés et de leur utilisation alimentaire, agricole, industrielle ou médicale.

⇒HYDROLOGIE, subst. fém.

Science qui a pour objet l'étude des eaux, de leur nature et de leurs diverses propriétés. Hydrologie marine; hydrologie continentale, fluviale. Un grand Service Soil conservation Service a été créé pour étudier la défense du sol. Ce Service a fait exécuter des études et des travaux relevant à la fois de l'hydrologie et de la météorologie (MAURAIN, Météor., 1950, p. 234).

— En partic. Hydrologie médicale. ,,Étude des propriétés et de l'utilisation thérapeutiques des eaux, naturelles ou artificielles`` (Méd. Biol. t. 2 1971).

REM. Hydrologue, hydrologiste, subst. Spécialiste en hydrologie. V. Colloque géogr. appl., 1962, p. 20.

Prononc. et Orth. : []. Att. ds Ac. dep. 1835. Étymol. et Hist. 1. 1614 « étude des eaux, de leurs propriétés » (LANDREY, Hydrologie, ou discours de l'eaue); 2. 1824 « étude des eaux minérales et de leurs propriétés thérapeutiques » (NYSTEN). Composé de hydro- et de -logie. Bbg. QUEM. DDL t. 1, 8, 14 (s.v. hydrologiste).

hydrologie [idʀɔlɔʒi] n. f.

ÉTYM. 1614; de hydro-, et -logie.

❖

♦ Didactique.

1 Étude des eaux, de leur composition, de leurs propriétés (⇒ Hydrotimétrie). || Hydrologie marine (⇒ Océanographie), hydrologie continentale (potamologie : hydrologie fluviale; hydrogéologie; glaciologie, etc.). || Hydrologie et hydrographie.