MODÈLE
Le langage de la philosophie aiderait peu à éclairer l’origine de la notion de modèle, qui a reçu un emploi très large dans la méthodologie des sciences. Cette origine est technologique: le modèle est d’abord la «maquette», l’objet réduit et maniable qui reproduit en lui, sous une forme simplifiée, «miniaturisée», les propriétés d’un objet de grandes dimensions, qu’il s’agisse d’une architecture ou d’un dispositif mécanique; l’objet réduit peut être soumis à des mesures, des calculs, des tests physiques qui ne sont pas appliqués commodément à la chose reproduite. De là, le terme a acquis une vaste portée méthodologique, pour désigner toutes les figurations ou reproductions qui servent les buts de la connaissance.
Il n’est pas nécessaire de remonter au sens platonicien, où le modèle était le «paradigme», la forme idéale sur laquelle les existences sont réglées: à ce sujet il y a un paradoxe qui fait que le modèle technique inverse la situation du modèle platonicien, puisqu’il est réalisation concrète au lieu d’être idée réalisable. Toutefois, la complexité de l’épistémologie autorise les glissements du sens. Il n’est pas interdit de concevoir que l’opération qui extrait d’une situation une figure de celle-ci permet en retour de fixer un type idéal et fournit un paradigme pour la reconstruction de cette situation. Ainsi, la physique de l’atome s’est développée autour du «modèle de Bohr», qui était d’abord une manière de schématiser les propriétés électriques de l’élément physique, d’unifier les effets spectraux des radiations qu’il émet. Au mieux, le modèle, dans les sciences évoluées, sert à fixer les lois sur un objet bien structuré, et cette fixation favorise à son tour la conception et l’expérimentation: les deux sens majeurs du terme de modèle, qui est une figuration et en même temps un schéma directeur, se recoupent et se conjuguent plus ou moins.
Quoi qu’il en soit, la doctrine de la science et de la technologie oblige à suivre les modèles dans la complexité de leurs types et dans la variété de leurs usages. Le modèle peut être une matérialisation des énoncés de la science dans un objet concret, presque autonome, que l’intuition ou la pensée ont des facilités pour cerner: la mécanique élémentaire réalisait les relations physiques dans des collections de particules auxquelles on assignait une forme et un mouvement pour mieux comprendre leurs interactions. Le modèle peut être aussi une transcription abstraite, mais contrôlée par la pensée logique et mathématique, d’une réalité concrète, empirique, dont l’étude directe ne donnerait que des relations approximatives. Ainsi l’économiste, le sociologue, le biologiste se donnent des «modèles théoriques» des faits qu’ils décrivent. Par exemple, l’économiste considère les décisions d’un «agent parfait» utilisant les informations selon le calcul des intérêts, et il peut remplacer les composantes d’une situation de concurrence par un «jeu stratégique», dans lequel chaque partenaire opère selon des matrices mathématiques de gains et de pertes. Il arrive enfin que le modèle participe de ces deux natures, qu’il soit prélevé sur un domaine d’objets particuliers et qu’il serve de fixateur pour les lois d’un autre domaine. C’est ce qui se produit quand on emprunte à une science déjà bien élucidée des modèles qui sont pris comme des «analogues» des propriétés étudiées par une science moins élaborée et permettent de prospecter les faits et les lois de celle-ci. Ainsi on a utilisé les lois des condensateurs électriques, en mettant en valeur des facteurs comme la différence de potentiel entre les pôles et la résistivité des milieux intermédiaires, pour interpréter certains des effets de la conductivité des membranes organiques, qui s’expriment dans le «filtrage» des substances assimilables.
Ces cas extrêmes de la modélisation se retrouvent, à l’état pur ou mélangé, dans les usages scientifiques décrits ci-dessous. Le modèle remplit deux fonctions majeures: il offre une contrepartie, dans l’ordre des structures figuralement claires, mathématiquement exactes, aux états de choses diffus que décrivent les sciences empiriques. Mais il intervient aussi en regard des élaborations théoriques, qui se présentent comme des suites de définitions nominales et de déductions formelles, et il fournit à celles-ci une référence objective qui peut consister dans une figuration géométrique ou dans un symbolisme algébrique. La modélisation entre donc en jeu aussi bien dans les sciences de faits que dans les sciences qui, comme les mathématiques, s’installent dans le registre des symboles.
Ce ne sont là que les cadres généraux dans lesquels se particularise la pratique des différentes sciences. On trouvera, ci-dessous, présentés par des spécialistes, les renseignements voulus sur la variété de ces emplois. On remarquera comment le mathématicien utilise des paradigmes purs au service de l’invention et, aussi bien, de la preuve; comment la physique et les sciences de la matière développent des modèles longuement élaborés, qui accompagnent les extensions de la théorie; comment les sciences de la vie et de l’homme, qui sont dans une situation empirique et théorique très ouverte, multiplient des modèles souvent partiels et provisoires pour donner une assise à leurs investigations. Les disciplines qui ont affaire avec la pratique humaine dans son acception la plus globale – les sciences sociales et esthétiques, par exemple – referment le cercle des modèles: en ce sens que ceux-ci, tout en leur servant de moyen d’analyse vis-à-vis des faits, orientent leur réflexion vers les formes directrices de la conduite et de la pensée humaines.
Et l’on sera ramené ainsi aux vues de la logique et de l’épistémologie sur lesquelles se terminera l’exposé. Avec la pratique des modèles se manifestent, en effet, certaines des conditions les plus actuelles de la construction du savoir: elle fait apparaître les voies de la recherche et de la codification des résultats, elle met en lumière le rôle principal des figures et des signes dans l’institution de la connaissance.
1. Le modèle mathématique
On sait, notamment depuis Cantor et Zermelo, que la plupart des notions de la mathématique peuvent être explicitées dans le cadre d’une théorie du premier ordre dont les axiomes affirment l’existence de certains objets appelés «ensembles» (cf. théorie élémentaire des ENSEMBLES). La réduction à laquelle il est fait allusion signifie, entre autres choses, qu’un nombre réel, une fonction analytique, une probabilité, un groupe, etc., peuvent être considérés comme des ensembles particuliers. Puisque cette théorie permet d’expliciter des notions aussi variées et notamment celle de modèle d’une formule, on doit s’attendre à ce qu’elle joue un rôle important pour notre propos. Néanmoins, les notions de la mathématique ont une existence, une portée concrète, indépendante de la réduction des mathématiques à cette théorie, comme d’ailleurs le montre le développement même de cette science.
Ainsi sommes-nous conduits à distinguer deux utilisations du mot modèle: celle du «mathématicien», qui se situe dans un univers de la théorie des ensembles; celle du «physicien», qui utilise les notions de la mathématique (y compris celles de la théorie des modèles) pour réduire, décrire, étudier le monde sensible ou celui qui est conceptualisé dans le langage naturel. C’est ce deuxième usage de l’expression «modèle mathématique» que l’on rencontre le plus fréquemment. Toutefois, il est intéressant de considérer le sens du mot «modèle» en mathématique pour analyser le caractère des notions qui permettent de le définir et, également, ses principales propriétés.
Différents sens du mot «modèle»
Le mot «modèle», en mathématique, est défini sans ambiguïté à partir de la notion de valeur d’une formule du calcul des prédicats du premier ordre dans une réalisation d’un langage, notions que l’on peut expliciter en théorie formelle des ensembles (cf. théorie des MODÈLES). La théorie des modèles a des applications dans divers domaines de la mathématique et cette théorie, développée par les logiciens, est qualifiée de sémantique dans la mesure où, d’une part, elle fait intervenir la notion de vérité d’une proposition et, d’autre part, s’oppose à la syntaxe qui se rapporte à la description des propositions mathématiques et des règles du raisonnement; le lien entre ces deux points de vue étant exprimé, notamment, dans le théorème de complétude.
Par contre, l’usage actuel de l’expression «modèle mathématique» dans diverses disciplines semble référer à un type de discours, plutôt qu’à un sens précis du mot «modèle». Si, par exemple, on considère la définition du corps des réels comme un modèle mathématique du «continu géométrique perceptible», et l’équation:

sur le corps des réels, comme un modèle de la surface que chacun peut construire et que l’on nomme «cubique réglée» (cf. GÉOMÉTRIE DIFFÉRENTIELLE CLASSIQUE, fig. 7), il est clair que l’on est en présence de deux «modèles mathématiques» de caractère différent et qui ni l’un ni l’autre ne ressemble d’ailleurs au modèle du phénomène de «propagation de la vague» constitué par la formule:

f étant une fonction deux fois différentiable de R2 dans R, etc. L’étude abstraite des modèles, ainsi d’ailleurs que leur construction, peut donc faire appel à des notions et des résultats de branches variées de la mathématique, logique, algèbre, analyse, probabilités, etc., et les modèles mathématiques constituent, pour les mathématiciens, une source de problèmes que l’on pourrait qualifier d’immédiats (immédiats au sens de naturels, mais pas au sens de simples: nombreux sont ceux qui ne sont pas résolus), par opposition aux problèmes (naturels également, mais d’un point de vue logique et non physique) qui naissent de l’étude des concepts et des objets que la mathématique considère et qui permettent notamment la formulation et l’analyse des modèles mathématiques. Pour chaque branche de la mathématique, pour chaque théorie même, il serait donc possible de donner une image, dans un domaine concret, de certains concepts, objets et résultats abstraits.
L’usage des modèles
L’abstraction est une réduction et, de ce fait, permet de faire apparaître des analogies entre des situations appartenant à des domaines habituellement séparés. Aussi n’est-il pas possible, dans les limites de ce texte, de recenser les différentes types de situations qui se laissent décrire et étudier de façon mathématique: nous renverrons pour ce point le lecteur aux aspects historiques des articles sur les théories mathématiques (cf. ALGÈBRE, CALCUL INFINITÉSIMAL, analyse COMBINATOIRE, CONVEXITÉ, équations DIFFÉRENTIELLES, GÉOMÉTRIE DIFFÉRENTIELLE CLASSIQUE, GROUPES (mathématiques) - Groupes de Lie, analyse HARMONIQUE, calcul des PROBABILITÉS, STATISTIQUES).
Bien que le domaine privilégié des modèles mathématiques soit celui de la physique, de la chimie, de l’astronomie, en un mot des sciences dites exactes et aussi de l’art de l’ingénieur où l’on pose des équations différentielles, on voit apparaître de plus en plus, dans des sciences autrefois qualifiées d’expérimentales – biologie, génétique, botanique –, y compris dans les sciences humaines – psychologie, linguistique, économie, sociologie –, l’usage de modèles mathématiques pour étudier les situations que l’on considère dans ces domaines [cf. SYSTÈMES DE TRANSFORMATIONS (THÉORIE DES)]. Ceci est possible dans la mesure où ces situations sont conçues avec une précision suffisante au détriment, d’ailleurs, des raccourcis intuitifs traditionnels plus immédiatement profitables et plus esthétiques de la littérature. Pour reprendre les termes de A. Régnier, «faire un modèle, c’est porter le discours scientifique au niveau de rigueur où la logique formelle des prédicats est valable, c’est donc d’abord définir, poser des concepts».
L’intérêt, la nécessité des modèles mathématiques varient avec les domaines. Si, par exemple, ils peuvent être la garantie de la solidité d’un ouvrage d’art, ils sont indispensables à la recherche fondamentale dans différentes branches de la physique moderne, qui a atteint un niveau d’abstraction élevé (cf. ATOME, PHYSIQUE, RELATIVITÉ), et ils permettent, ce qui est un avantage appréciable dans les sciences humaines, de rapprocher des phénomènes apparemment étrangers, de mettre en cause ou d’évaluer l’importance relative des concepts du langage que l’on utilise pour rendre compte du phénomène observé (cf. chap. 6 et 7, ainsi que CYBERNÉTIQUE, théorie des JEUX, etc.).
Toutefois, l’on se doute bien que le discours mathématique ou logique a un champ d’application qui n’est pas illimité, c’est, entre autres choses, ce que M. Gergonne, après Pascal, souligne dans la citation suivante par laquelle nous terminerons ces quelques remarques: «Platon regardait, dit-on, celui qui savait bien définir comme participant de l’intelligence divine, et Pascal n’a pas hésité à regarder l’impossibilité où nous sommes de tout définir comme la source unique de l’incertitude de nos connaissances.»
2. Le modèle en physique
On peut établir un intéressant parallélisme entre l’utilisation des modèles en physique et dans les autres sciences exactes ou humaines. Il n’empêche que la signification d’un modèle présente, en physique, une résonance et une portée propres à cette discipline. La notion de modèle soulève, en effet, la question même de l’objectivité d’une science, soucieuse d’atteindre une «réalité» et des lois indépendantes de toute intervention du sujet et dépassant, par conséquent, l’idée d’une construction des possibles, d’une interprétation des apparences au moyen de modèles.
C’est pourquoi l’histoire du «modélisme» revêt en physique, singulièrement avec Giordano Bruno et Galilée, un caractère qui peut être primordial, car il déborde les méthodes de la physique pour mettre en cause son objet et sa signification.
Schéma simplificateur et construction d’ensemble
La construction de l’objet d’une loi physique ne peut s’effectuer sans distinguer, parmi la complexité des données sensibles, l’essentiel de l’accessoire. On assimile donc le contenu de l’expérience à une construction hypothétique qui procède d’un schéma simplificateur. C’est à partir de ce «monde archimédien» que le physicien essaie de retrouver les apparences, tout au moins dans le domaine auquel il se limite. À ces esquisses simplifiées s’appliquent les lois de la mécanique. Il peut travailler sur ces schémas pour éprouver les conséquences de ses postulats et retrouver ainsi les apparences. D’où le nom de «modèles», conçus alors comme des «canevas» qui se substituent, provisoirement, à la trop grande complexité de la nature.
Sans être en contradiction avec l’expérience effective, les modèles se proposent d’en donner une simplification systématique. Tels sont les modèles de Galilée écartant les «empêchements extérieurs» pour s’appliquer à des expériences idéales. Toute expérience de pensée constitue, en ce sens, l’exploitation logique d’un modèle.
Notons qu’à cet égard toute la physique – et même la perception naïve – s’applique forcément à des modèles plus ou moins structurés. Soulignons aussi que ce modélisme implique un jugement, un point de vue, pour cautionner les traits «essentiels» du modèle. Le progrès de la physique consiste souvent à réviser certains agencements d’autant plus tenaces qu’ils sont plus ignorés.
Une autre caractéristique du modèle est de constituer, dans un domaine déterminé, parfois restreint, un schéma complet. En cela, le modèle se distingue de l’hypothèse simplificatrice qui peut être adjointe à l’ensemble d’une théorie sans en altérer le caractère. Le modèle se présente comme une structure dont les articulations restent solidaires. Bien entendu, un modèle similaire peut être proposé, mais la modification d’un détail influence l’ensemble, peut-être même de façon infime.
Ainsi les multiples rouages formant le cosmos de Ptolémée présentent une unité d’ensemble. On peut, compte tenu des progrès de l’expérience, modifier la position du centre d’un déférent, adjoindre un épicycle, inventer l’équant: il convient alors de s’assurer que l’ensemble, ainsi perturbé, forme une nouvelle machine adéquate, c’est-à-dire adaptée, à l’ensemble des apparences.
La construction d’un «modèle» associe toujours un schéma géométrique à une loi élémentaire de composition. Cet ensemble ne bénéficie pas, en général, d’une véritable unicité qui en justifierait la nécessité. Bien entendu, la complexité d’un modèle dépend d’un certain stade d’expérimentation. Le monde de Ptolémée introduit les rouages plus complexes que le monde d’Eudoxe de Cnide. En ce sens, il existe une hiérarchie des modèles.
Néanmoins, pour un même stade d’expérimentation, on peut en général interpréter l’ensemble des apparences par une pluralité de constructions associées à des lois élémentaires distinctes. En effet, retrouver les apparences consiste à fixer les paramètres ou, si l’on préfère, les degrés de liberté de mécanismes sous-jacents. Or ce résultat peut être acquis de plusieurs manières et cela d’autant plus que les éléments constitutifs du modèle sont plus nombreux et les règles d’ajustement plus souples.
Supposons, par exemple, qu’une orbite circulaire ne réussisse pas à décrire les apparences du mouvement d’une particule: on peut augmenter le nombre des paramètres de la trajectoire en choisissant une ellipse; on peut aussi obtenir le même nombre de degrés de liberté en associant deux orbites circulaires. Bien entendu, la distribution d’un certain nombre de paramètres suivant différents modèles conduit à rejeter certains d’entre eux; il est cependant impossible d’affirmer qu’on est parvenu à sélectionner le seul modèle possible. Ainsi Averroès dénonçait, au XIIIe siècle, le scandale qui consistait à admettre à la fois les opinions d’Aristote et de Ptolémée, opinions philosophiquement incompatibles mais que l’on croyait simultanément acceptables, pour reconstruire les apparences.
En ce sens, et en faisant de la physique la science d’un possible compatible avec ces apparences, l’objet de la physique se réduit toujours à un «modèle»; et cette manière de parler, comme l’assure le cardinal Bellarmin, «avec un excellent bon sens et sans courir aucun risque, est suffisante pour un mathématicien» (lettre à Paolo Foscarini, in Le Procès de Galilée ). Aussi, reconnaît P. Duhem, «à supposer que les hypothèses de Copernic aient pu expliquer toutes les apparences connues, il fallait en conclure non pas qu’elles étaient nécessairement vraies, mais qu’elles pouvaient l’être». L’«objet» de la physique ne pourrait être logiquement dissocié de la pluralité des modèles et, par conséquent, de leur contingence.
Dans la physique mécaniste
Jusqu’ici, le modèle est apparu comme un schéma simplificateur. Néanmoins, ce canevas se situe au niveau même des apparences qu’il prétend analyser. Il en constitue une version plus dépouillée mais, en même temps, plus quantitative et plus utilisable, tout en restant du même type. Autrement dit, le mouvement apparent des planètes se déduit de mouvements élémentaires plus simples, mais ce «modèle» ne constitue pas un mécanisme caché responsable d’apparences (couleur, son, champ électrique) dont la nature serait totalement différente de la figure et du mouvement auxquels se limite le modèle.
Au contraire, le but de la physique mécaniste est d’essayer, par des voies d’ailleurs très différentes, une telle assimilation. En réduisant tous les phénomènes «à la figure et au mouvement», Descartes va accentuer l’ambiguïté liée à la notion de modèle. Le modèle va être délibérément conçu comme une représentation du possible, comme une parabole destinée à suggérer les propriétés véritables des corps. Ainsi la lumière est représentée presque indifféremment comme la pression qui se transmet instantanément le long du bâton de l’aveugle, comme le vin dont les filets s’éparpillent à travers les raisins de la cuve, comme des petites billes rigides qui obéissent à une balistique des corps matériels.
Le modélisme issu des principes cartésiens semble même renoncer au monde archimédien, certes simplifié, mais non contradictoire de la physique galiléenne; le modèle peut présenter des caractères incompatibles avec les postulats initiaux. Tout en justifiant les lois de l’optique géométrique – réflexion et réfraction – par des modèles balistiques, imaginant le rebondissement de petites balles rondes et dures, Descartes soutient que la lumière ne saurait être le mouvement d’un corps, mais une «tendance au mouvement», une pression immédiatement ressentie dans un univers incompressible et plein. L’identité des lois qui régissent les phénomènes «en puissance» et «en acte» lui permet, cependant, l’usage de véritables paraboles balistiques, sans aucun lien avec des mouvements vrais, effectifs, puis le passage à la limite.
Un modélisme assez différent interprète la formation des couleurs par la grosseur des particules, par leurs vitesses relatives, par leurs mélanges, par une complexité morphologique ou cinétique inhérente à la constitution du rayon lumineux.
Il s’agit moins alors d’induire des lois inconnues à partir de dispositifs simplificateurs que d’interpréter des propriétés, souvent fort bien établies, au moyen de mécanismes élémentaires sous-jacents réputés plus simples: la loi des sinus précède les modèles balistiques qui veulent l’expliquer; les équations de Maxwell gouvernent l’électromagnétisme en dépit de l’échec des modèles d’éther. Néanmoins Maxwell et surtout W. Thomson se croient obligés d’interpréter les équations du champ par des mécanismes simples appliqués à un hypothétique substrat.
Ce type de modélisme est vivement condamné par Auguste Comte: «Toute hypothèse physique, pour être jugeable, affirme-t-il, doit exclusivement porter sur les lois des phénomènes et jamais sur leur production.» Cette opinion semble restreindre l’utilité du modélisme à l’établissement de corrélations du même type. Autrement dit, s’il est légitime de réduire un mouvement apparent complexe à des mécanismes élémentaires simples, il est abusif de justifier les lois de Maxwell par l’introduction de modèles d’éther, aussi artificiels qu’hypothétiques. D’une manière analogue, les prétentions explicatives d’un mécanisme à base de modèles suscitent les protestations de Duhem. Un modèle a-t-il, par lui-même, une vertu explicative qu’il n’ait puisée, auparavant, dans l’expérience? Déjà, au XVIIe siècle, le père Ango soutenait, suivant Aristote, que si les modèles mécaniques peuvent interpréter les propriétés de la lumière, ils ne prétendent aucunement en élucider la nature. Ces discussions, qui nous ramènent au défi galiléen sur l’objectivité de la physique, prennent une acuité particulière dans la querelle qui oppose Mach à Planck et aux partisans de l’atomisme. On sait que celui-ci devait renvoyer dos à dos les protagonistes d’un positivisme figé et d’un modélisme vieilli.
Structures et modèles
La prédominance historique des modèles issus de la mécanique semble associer tout modélisme à une construction dans l’espace, construction dont les éléments satisfont à des règles bien connues (lois du choc, inertie, principes de conservation, etc.). Néanmoins, une forme assez différente de structuration de l’expérience fut, de tout temps, pratiquée. Elle consiste à mettre en évidence certaines opérations qui permettent de définir mathématiquement et a posteriori leurs objets. Telles sont les notions de force, de champ, de groupe. Elles constituent alors des structures dynamiques, mathématiquement bien définies et susceptibles de rejoindre l’expérience.
On a opposé structures et modèles comme on oppose théories à principes et théories à images. En fait, cette disposition est beaucoup trop simpliste car, si un modèle mécanique requiert forcément une loi de composition, une sorte de «mode d’emploi», l’acquisition d’une nouvelle structure s’incarne nécessairement dans des observables d’espace ou de temps. D’ailleurs, il est d’autant plus difficile de séparer les modèles de structures dynamiques plus abstraites qu’il s’agit d’un formalisme plus complexe et plus mathématique. Par exemple, les «modèles cosmologiques» actuels jouent un rôle très différent des anciens modèles d’éther. S’ils doivent, eux aussi, s’insérer dans un certain nombre d’équations aux dérivées partielles, ce n’est pas pour se substituer à la géométrie et pour en donner une version mécaniste simplificatrice. Les notions de «fluide parfait», de «rotations», de «cisaillements», les «conditions de symétrie» s’incarnent dans des formes très éloignées des données concrètes de la mécanique classique. La matière, comme le champ, se résout en structures qu’il est difficile d’assimiler aux anciens modèles et qui, cependant, n’en sont pas totalement disjointes.
Il n’empêche qu’on peut distinguer deux familles d’esprits, soucieuses de rattacher «le simple fait» à un modèle simple auquel s’appliquent des lois connues, ou bien à une opération suggérée par l’expérience et génératrice de ses propres définitions. Ampère et Faraday sont des représentants typiques de chacune de ces tendances: Ampère veut expliquer l’effet Œrsted (lignes de force circulaires créées par un courant électrique) par l’introduction de pôles auxquels on sait appliquer des lois connues; Faraday se refuse à abandonner l’essentiel des données expérimentales sous prétexte qu’elles ne sont pas mathématisables. Ainsi va naître l’idée de «champ», notion qui, chez Faraday, n’est plus tout à fait un modèle mécanique, mais pas encore une structure mathématique.
Notons que les structures dynamiques partagent les prérogatives et les inconvénients des «modèles».
– Valeur intuitive : affirmer avec Newton que «la lune tombe», prétendre avec Einstein qu’un point matériel, soumis aux forces de gravitation, se déplace librement dans un espace-temps courbe, procède d’une intuition dont le pouvoir de synthèse est bien supérieur au prestige des circulaires.
– Construction d’ensemble : les structures dynamiques accompagnent toute structuration fructueuse. On sait l’extension, souvent abusive, que donne au newtonianisme la physique attractionnaire du XVIIIe siècle. Les théories du champ, la théorie des groupes ont été, elles aussi, conduites à une politique conquérante.
– Pluralité : il est évident qu’une répartition arbitraire des paramètres peut affecter une structure mathématique aussi bien que les modèles primitifs. Ainsi peut-on imaginer que les propriétés des particules élémentaires peuvent se déduire de divers groupes concurrents. S’il existe une hiérarchie de ces possibilités, elle est très loin d’aboutir actuellement à l’unicité d’une solution.
Notons d’ailleurs que le traitement de l’information par les ordinateurs et la mise au point de «programmes» préalables compliqués ne sont pas sans lien avec la diffusion de modèles opératoires. Ainsi naissent, meurent ou progressent d’éphémères «modèles» dont la paramétrisation est fixée par le programme et dont l’ordinateur permet de tester la cohérence et l’efficacité.
Hiérarchie des modèles. Modèles et objets
La notion de modèle est associée à une idée de simplification systématique, d’ensemble organisé, de structuration des possibles. Dans une certaine mesure, le modèle semble ainsi s’opposer à l’objet comme le possible et le provisoire s’opposent au nécessaire et au permanent. En fait, un modèle possède toujours une certaine plasticité. Il représente, bien entendu, une distribution donnée de paramètres et de degrés de liberté. Toutefois, il est possible de concevoir une distribution différente de ces mêmes paramètres (ou d’un nombre plus grand), distribution ajustable à une expérience ultérieure ou même à une situation expérimentale identique.
On pourrait donc penser qu’un modèle est d’autant meilleur que sa plasticité est plus grande. En augmentant indéfiniment le nombre des rouages d’une construction (et des paramètres d’une loi physique), on pourrait adapter le modèle à un contexte expérimental sans cesse élargi.
Toutefois, le rôle de la physique ne consiste pas à suivre pas à pas les méandres de l’expérimentation pour les incorporer dans une description servile. Au contraire, une explication est d’autant plus convaincante qu’elle s’éloigne davantage des apparences pour les retrouver ensuite, comme des conséquences nécessaires et quantitatives, issues nécessairement, c’est-à-dire univoquement, de ses principes. Aussi une théorie est d’autant plus «explicative» qu’elle introduit un modèle plus rigide, qu’elle contient moins de paramètres arbitraires. C’est à la limite seulement qu’elle cesse d’être étalonnée par l’expérience et qu’elle permet de prévoir l’expérience . C’est à cette condition que le «modèle» se transforme en «objet».
D’autre part, une théorie «objective» ne doit pas cette qualité à l’adoption ni même à l’utilisation d’un formalisme ou d’un principe réputé simple, simplicité bien difficile à définir et à justifier. C’est en essayant de résorber l’aspect phénoménologique des apparences dans une description (géométrique, analytique) d’où les particularités provenant de l’observation sont progressivement exclues, c’est dans cette marche vers ce qu’Einstein appelle l’«extra-personnel» que la physique reconquiert le particulier et impose son objet.
Néanmoins, s’il est aisé d’esquisser pratiquement les traits des «modèles» de la physique, si l’on peut facilement dénoncer leur caractère éphémère et polyvalent, les assimiler à des ballons d’essai acheminant à des constructions moins fugaces, une séparation radicale entre modèle et objet n’est pas sans danger. Elle pourrait introduire, renouvelant les vieilles querelles, une regrettable dichotomie entre le domaine du «comment», régi par le modèle et concédé à la physique et celui du «pourquoi», abandonné à la philosophie ou bien au scepticisme.
D’autre part, toute assimilation de l’objet au modèle ne risque-t-elle pas de disqualifier la physique dans l’essentiel de ses recherches? Il ne semble pas, mais une telle discussion sort du cadre de cette étude.
Si la physique, science des apparences, ne peut logiquement ni pratiquement se désolidariser d’un «modélisme», elle assure progressivement et de façon univoque son objectivité. Jouant sur la diversité et sur la plasticité des modèles, elle dégage une voie qui définit sans équivoque possible, mais de façon dynamique, la validité de son objet et l’invariance de ses lois.
3. Le modèle dans les sciences de la Terre
Les sciences de la Terre se proposent d’aboutir à une description du globe sur lequel vivent les hommes.
Le souci d’objectivité qui doit les animer paraît s’opposer à la considération de modèles conçus a priori; l’usage de ceux-ci est cependant nécessaire pour analyser les relations entre les aspects différents d’un même phénomène, mais leur portée ne doit pas être surestimée.
La géologie et la classification naturaliste
La géologie est née comme une des branches des sciences naturelles; et l’idéal de celles-ci, formées pour l’étude des êtres vivants, est la prééminence de l’observation. Pour décrire, nommer et classer, il suffit d’observer les objets fournis par la nature, et il n’y a point à y substituer un modèle construit par l’esprit. Même lorsqu’on compare des espèces différentes, pour les grouper en genres, familles ou ordres, ces groupements ne sont point conçus comme des modèles idéaux, dotés de certains caractères, et indéterminés quant à ceux qui varient d’une espèce à l’autre. C’est à partir d’une espèce type que l’on définit le genre, qui est conçu comme un groupement d’espèces réelles, non comme un ensemble abstrait de caractères qui leur seraient communs.
La géologie s’est inspirée de cette méthode, non sans quelques difficultés, dues à ce qu’en l’absence des phénomènes de la reproduction, les limites de l’espèce ne s’imposent pas. Par exemple, il a fallu réagir contre la tendance à décrire et à nommer toutes les roches magmatiques, les différences qui les séparaient pouvant n’être pas significatives. Pour les familles retenues, il n’existe le plus souvent plus de type, et chaque roche réelle présente quelques caractères particuliers, même si elle répond pleinement à la définition de cette famille. Ne pourrait-on dire qu’au type s’est substitué un modèle idéal, défini par un nombre limité de caractères? Ou faut-il plutôt considérer que la famille est simplement définie par une liste de caractères? De même, une notion comme celle d’anticlinal est définie par quelques caractères qui peuvent appartenir à des structures très différentes; on peut en décrire des exemples, non en construire un modèle.
La géophysique
À cette méthode traditionnelle de la géologie, qui se refuse à la construction de modèles, suspects d’être à la fois arbitraires et artificiels, s’oppose la méthode de la géophysique.
Dès que l’on envisage une grandeur physique mesurable, telle que le temps de parcours d’une onde sismique, un champ magnétique, l’intensité de la pesanteur, dont la valeur dépend de la distribution de certaines propriétés dans un espace étendu, on est conduit à construire un modèle, c’est-à-dire à imaginer un corps jouissant de celles des propriétés de la Terre qui sont bien connues (forme extérieure, vitesse de rotation, etc.) et pour lequel des hypothèses précises définissent la distribution des propriétés intéressées, d’une manière telle qu’il soit possible d’en déduire par le calcul les grandeurs qui, pour la Terre, sont susceptibles d’être mesurées.
Dès 1743, pour étudier l’aplatissement de la Terre, qui devait permettre de vérifier la théorie de Newton, Alexis Clairaut considérait ainsi un globe fluide, en rotation comme la Terre, soumis comme elle à sa propre attraction, et calculait l’aplatissement de sa surface, montrant qu’il n’était égal à celui qui venait d’être mesuré pour la Terre que pour un écart notable de densité entre le centre et la surface [cf. GRAVIMÉTRIE]. Malgré les différences essentielles entre ce modèle et la Terre, que constituent l’existence du relief à la surface de celle-ci et la rigidité qu’il implique, c’est là une indication précieuse, et dont on a toujours tenu le plus grand compte; rien n’imposait d’ailleurs de choisir d’emblée entre deux interprétations: celle d’un comportement actuel de la Terre, en partie analogue à celui d’un fluide, et celle d’une fluidité initiale, qui aurait été suivie d’une solidification.
Citons encore le modèle utilisé en sismologie, pour lequel on admet que la vitesse des ondes sismiques ne dépend que de la profondeur. On peut alors facilement, pour une loi donnant la vitesse en fontion de la profondeur, calculer la durée de trajet d’une onde de volume entre deux points de la surface, qui sur la Terre est directement accessible aux mesures. Mais on peut aussi, sur ce modèle, réaliser une opération plus complexe, qui est l’inversion de ce calcul, par laquelle on détermine la distribution des vitesses en fonction de la profondeur; cette distribution fournit une loi des temps de parcours en fonction de la distance, qui doit être conforme aux résultats d’observation.
Il ne faut cependant pas confondre les résultats de cette inversion avec un calcul direct qui permettrait de déduire de la mesure des temps de parcours en surface l’échelonnement des vitesses en profondeur. Le résultat n’a de sens que dans le cadre du modèle qui a été défini, formé de couches concentriques homogènes, et pour lequel on suppose de plus que la vitesse va toujours en croissant avec la profondeur. L’inversion peut poser des problèmes, comme de savoir si la solution trouvée est la seule possible, ou de déterminer de combien la solution pourrait être modifiée par les petites erreurs qui affectent inévitablement les données; la question s’est posée, par exemple, de savoir dans quelle mesure l’existence de discontinuités de vitesses à certaines profondeurs devait être considérée comme établie, ou avait pu être suggérée par les méthodes de calcul employées.
On a été conduit à perfectionner ce modèle, pour rendre compte d’autres types de vibrations, tels que les ondes superficielles, dont la vitesse dépend de la fréquence, et les vibrations propres de la Terre. Mais on a été obligé d’admettre une décroissance des vitesses sismiques vers 150-200 km de profondeur, exclue a priori par le modèle primitif, mais qui s’est avérée parfaitement compatible avec les observations.
Si on veut faire intervenir dans un tel modèle encore d’autres données, telles que l’aplatissement, les moments d’inertie, la gravité, etc., on est conduit à supposer un lien entre les différentes propriétés de la matière que l’on envisage, telles que la densité, les caractéristiques élastiques, en s’inspirant des relations connues pour les corps réels (équations d’état), ce qui ramène à des hypothèses sur la composition chimique et minéralogique et permettra de calculer la pression. Mais, si l’on fait intervenir des propriétés aussi variées, l’inversion n’est plus possible par un calcul direct. Il reste la possibilité d’avoir recours à une méthode «de Monte-Carlo», c’est-à-dire de se donner au hasard, dans certaines limites, les propriétés caractéristiques du modèle, d’en déduire par le calcul les effets mesurables en surface, et de ne retenir la solution que si l’on retrouve les valeurs mesurées. Si, sur quelques centaines de milliers de solutions essayées, on peut en retenir une vingtaine, elles donnent, par leurs écarts, une idée du degré d’approximation atteint; il va sans dire que de tels calculs ne sont possibles qu’à l’aide d’ordinateurs à grande capacité. Mais on devra toujours se demander si, parmi les hypothèses faites sur le modèle, il n’y en a pas qui ont écarté d’autre solutions, peut-être aussi satisfaisantes que celles qui ont été obtenues. Le seul fait d’avoir à se poser cette question empêche d’identifier le modèle retenu avec une image de la Terre réelle; cela d’autant que l’on a négligé les différences de structures régionales, qui se traduisent par l’opposition entre continents et océans.
Il faudra, pour analyser ce rôle du relief superficiel, d’autres modèles, qui resteront nécessairement schématiques à divers points de vue. De tels modèles sont utilisés en géodésie, pour schématiser l’effet du relief et de sa compensation isostatique sur le champ de gravité; mais les techniques de calcul employées obligent à présupposer que l’effet de cette compensation ait une symétrie de révolution par rapport à l’élément de relief considéré. Cette restriction empêche de prendre en considération le rôle que pourraient jouer les cassures majeures, dont l’influence est cependant évidente pour toutes les structures superficielles. Même si, par ailleurs, ces modèles s’inspirent de certains phénomènes géologiques réels, on ne peut donc y voir que des images très éloignées de la structure réelle. Malheureusement, et ceci se produit trop souvent, beaucoup de géologues, impressionnés par la masse des calculs auxquels ces modèles donnent lieu et par leur précision apparente, peu au fait des servitudes techniques qui ont présidé à leur choix, risquent de s’y fier comme à des représentations valables de la réalité.
C’est un fait d’expérience que, lorsqu’un modèle, choisi primitivement d’une manière très largement hypothétique et arbitraire, a fait l’objet d’un gros travail théorique d’élaboration, il acquiert de ce seul fait, aux yeux de beaucoup, un degré de vraisemblance hors de proportion avec sa véritable signification. La chose est particulièrement nette pour la question des températures intérieures du globe. Les données dont on dispose pour les évaluer sont très insuffisantes, et l’on est pratiquement forcé de faire concourir à cette estimation les hypothèses que l’on peut faire sur leur évolution, pour tenir compte tant du refroidissement par conduction et par convection que de la chaleur dégagée par la radioactivité. Cela implique la construction d’un modèle, pour lequel on calcule cette évolution, et l’on constate qu’il est indispensable, pour le définir, de faire une hypothèse sur la répartition des températures lors de la formation de la Terre, il y a 4,55 milliards d’années. Si les modèles sur lesquels on a travaillé supposent la Terre froide à l’origine, beaucoup seront tentés de prendre cette hypothèse comme démontrée, alors que, si l’on a envisagé une origine à chaud, on peut construire également des modèles rendant compte des données actuelles. On a tendance à confondre le modèle, construit pour tester les conséquences d’une hypothèse, avec une représentation conventionnelle de la réalité, du moment qu’il ne fait pas apparaître de contradiction, sans se demander si l’on ne pourrait pas en imaginer d’autres.
Les modèles et l’analyse des processus géologiques
On a souligné plus haut l’opposition traditionnelle entre la géophysique, qui, parce qu’elle étudie des phénomènes susceptibles d’une représentation mathématique, doit raisonner sur des modèles définis d’une manière précise, et la géologie, qui s’est d’abord proposé de décrire et de classer, conformément aux méthodes des sciences naturelles; mais la géologie s’efforce aussi de reconstituer les phénomènes du passé, qui sont à l’origine des roches et de leur disposition.
Le plus souvent, ce qu’on sait de ces phénomènes ne permet pas d’en représenter mathématiquement le déroulement, et il peut sembler que cela dispense de définir le modèle qui servira à les figurer. Mais, que l’on raisonne par analogie ou que l’on évoque certaines des particularités de ces phénomènes, on se réfère, implicitement, à une certaine image mentale, et le fait, que cette image – ce modèle – reste imprécise, risque d’être une source de confusions et d’incertitudes. Cela joue aussi bien en paléontologie – où toute considération sur la succession des espèces implique un modèle de l’évolution des espèces et de la sélection naturelle, qui reste souvent sous-entendu – que dans les branches les plus variées de la géologie. Lorsqu’un pétrographe considère la proportion et la nature des éléments détritiques dans une roche sédimentaire, il se réfère implicitement à un modèle de la mer dans laquelle s’est fait le dépôt; il ne tirera tout le bénéfice possible de la comparaison avec les mers actuelles que s’il précise suffisamment le modèle, pour pouvoir lui appliquer ce que l’on sait des mécanismes de transport.
On pourrait multiplier les exemples: éviter de proposer un modèle explicite, c’est souvent s’en tenir à une image inconsciente, imprécise, qui encourage le verbalisme et entretient la confusion, puisque le lecteur ne sait pas exactement quel est le modèle auquel se réfère l’auteur, et l’imagine souvent tout différent. La chose est particulièrement nette en tectonique, où l’on s’efforce, par souci d’objectivité, de limiter la description aux faits constatés et de fonder sur eux la reconstitution des mouvements, alors que des hypothèses sur leurs rapports avec les parties profondes, non directement observables, sont sous-jacentes à toutes les interprétations, sans qu’on ose les formuler explicitement.
Les déductions qui apparaissent en géologie, dès que l’on ne se borne plus à décrire mais que l’on tente de reconstituer les phénomènes générateurs, gagneraient en clarté si l’on formulait plus explicitement les hypothèses qui définissent le modèle sur lequel on raisonne, même s’il faut envisager plusieurs modèles, pour choisir entre eux, ou pour constater l’indétermination que laissent subsister les observations dont on dispose.
Les succès de modèles géophysiques relativement simples pour décrire la tectonique des plaques et la genèse des fonds océaniques ont incité les géologues à s’en inspirer. Des modèles géochimiques ont été proposés pour représenter l’origine et les relations de roches d’origine profonde, profitant de ce que de petites différences de compositions isotopiques permettent de suivre certains éléments, au cours de transformations même très complexes. Il y a un risque de prendre ces modèles globaux pour la représentation d’une réalité, qui est en fait certainement beaucoup plus complexe, alors que leur seule utilité est de mettre en évidence la nature des corrélations entre les facteurs qu’ils prennent en compte.
À mesure que se précisent les exigences de rigueur dans le raisonnement, on voit s’estomper l’opposition qui pouvait apparaître entre la géologie et la géophysique dans la manière traditionnelle de faire appel à des modèles. Dès qu’on dépasse la description et la classification pour aborder l’analyse des processus, celle-ci implique une référence à un modèle, dont la définition doit être d’autant plus précise que les raisonnements qu’on lui applique sont plus élaborés. Si les déductions mathématiques exigent une définition complète, même des raisonnements plus qualitatifs ou par analogie demandent, pour être valables, une définition suffisante du modèle.
Mais définir le modèle sur lequel on raisonne, c’est en même temps fixer des limites, en précisant ce qui n’a pas été pris en considération, et qui ouvre la voie à des recherches plus approfondies.
4. Le modèle en biologie
Le modèle est une représentation schématique d’un objet ou d’un processus qui permet de substituer un système plus simple au système naturel. Cette définition conduit à considérer deux aspects du modèle:
– le modèle concret , construit à partir des données expérimentales, qui rend compte aussi fidèlement que possible de certaines des propriétés, géométriques ou fonctionnelles, de l’objet et des lois auxquelles il est soumis;
– le modèle théorique , qui permet d’élaborer, à partir du modèle de l’objet, une théorie qui ramène le phénomène étudié à un phénomène plus général, en accord avec l’expérience et confronté avec elle, ce concept faisant une plus grande part à l’hypothèse.
Dans quelle mesure la biologie utilise-t-elle ces schémas simplificateurs? Comme les autres sciences de la nature, elle a été pendant longtemps une science purement descriptive, s’attachant à observer, classifier, puis à comparer. Aussi n’est-il pas étonnant que le biologiste, pour expliquer – ou tenter d’expliquer – les phénomènes qu’il observait, ait cherché à les rapprocher de systèmes qui présentaient avec eux des caractères de similitude et dont les lois étaient mieux connues. La comparaison entre le cœur et la pompe n’est pas une simple image; elle a permis à Harvey de prouver que la circulation du sang relevait des lois de l’hydraulique. Lavoisier, en établissant sa célèbre analogie entre la respiration et la combustion, montrait qu’une fonction physiologique pouvait être analysée suivant les concepts de la physique et de la chimie.
La notion de modèle n’a pris toute son importance que lorsque la biologie a commencé à utiliser les techniques et les modes de pensée et de raisonnement de la physique.
La méthode de diffraction par les rayons X, grâce au perfectionnement de la méthodologie et à l’emploi des calculateurs, a permis de réaliser des modèles de structures moléculaires de plus en plus complexes. En outre, au cours des dernières années, le développement de l’informatique et son application à la biologie ont introduit une nouvelle conception du traitement des données expérimentales; cette conception permet de rendre compte, à l’aide de schémas modèles, des réactions multiples, simultanées, du fonctionnement de la cellule par exemple, à partir d’une quantité réduite d’informations et d’hypothèses sur les mécanismes possibles.
Mais, avec l’apparition de la cybernétique, la notion de modèle apparaît comme essentielle. En fait, cette science, qui a établi ses principes fondamentaux à partir de l’observation d’êtres vivants, a pour but, dans son application à la biologie, de construire des modèles qui simulent des systèmes biologiques des êtres vivants ou certaines de leurs fonctions, afin d’expliquer leur comportement et éventuellement de prévoir les insuffisances de ces systèmes.
Les types de modèles utilisés
Le modèle tel qu’il a été défini précédemment implique la notion d’analogie, c’est-à-dire de similitude de certains caractères. Il doit satisfaire à des critères dont le choix dépend évidemment du but recherché. Un même système pourra être représenté par plusieurs modèles suivant qu’on le considère par exemple sous l’angle de la structure ou sous l’angle de la fonction. Mais le modèle ne traduit pas toutes les possibilités de l’objet: il ne répond donc qu’à un nombre limité de critères, sinon il serait identique à l’objet. Cette limitation lui confère son caractère de schéma simplificateur.
On peut classer les différents types de modèles suivant la nature des critères de similitude.
– Les modèles physiques proprement dits, qui sont des analogues géométriques, mécaniques ou électriques, et sont définis par l’invariance du rapport de certaines grandeurs ou de propriétés homologues. À ce type de modèle, on peut rattacher les modèles qui utilisent des critères naturels, en substituant l’animal à l’homme, ou la bactérie aux êtres organisés. Les modèles électriques, analogues à des systèmes physiques, constituent une classe particulière de modèles pour lesquels s’ajoutent, aux critères de similitude physique, des similitudes de fonctionnement. C’est sur cette similitude de fonctionnement qu’est basé le principe des «simulateurs analogiques».
– On passe insensiblement de la notion précédente du modèle au concept plus abstrait de modèle par simulation à l’aide d’un ordinateur (computer simulation model) ; celui-ci est un modèle «numérique» dans lequel ce sont les équations traduisant les caractéristiques du fonctionnement qui sont invariantes.
– Enfin, les modèles cybernétiques , qui sont caractérisés essentiellement par leur mécanisme de contrôle (feed back ). Les critères de similitude dans ce cas porteront sur la comparaison des performances.
Modèles de structure
Au niveau de la molécule
Au niveau de la molécule, le modèle de structure est une construction géométrique qui figure l’arrangement dans l’espace des atomes ou groupes d’atomes dont est constituée la molécule. Les liaisons interatomiques et les angles que font entre elles ces liaisons étant calculées par ailleurs sur des molécules plus simples, le modèle est édifié à partir des données expérimentales de la diffraction par les rayons X, en tenant compte des lois de la chimie, du rayon d’action des atomes, des angles de valence, etc. On le confronte alors à l’expérience: le diagramme de diffraction que devrait avoir une telle structure est calculé et comparé avec le diagramme de diffraction obtenu expérimentalement. Le modèle est modifié jusqu’à ce qu’il rende compte aussi parfaitement que possible des résultats de l’expérience.
L’application de cette méthode par tâtonnements (trial and error ) aux protéines fibreuses devait permettre à L. Pauling de prédire la structure régulière et périodique de la chaîne enroulée en hélice 見 dont les spires sont maintenues entre elles par des liaisons hydrogène parallèles à l’axe.
De telles structures peuvent être matérialisées (fig. 1). Dans le modèle compact, les atomes sont représentés par des boules dont les rayons sont proportionnels aux rayons de Van der Waals. D’autres modèles, réalisés à l’aide de simples tiges métalliques figurant seulement les liaisons interatomiques, constituent des modèles «squelettes», qui permettent d’avoir une vue de la disposition intérieure de la molécule. Ces modèles sont de vrais jeux de construction dont l’importance, en tant qu’outils de travail, est soulignée par J. D. Watson dans son livre sur La Double Hélice .
L’établissement de modèles structuraux a nécessité une somme de calculs considérable, dans le cas des protéines globulaires en particulier: ceux de la myoglobine (J. C. Kendrew) et de l’hémoglobine (M. F. Perutz) ont demandé plusieurs années de travail. À l’heure actuelle, grâce au perfectionnement des techniques, on a pu établir la structure d’une centaine de protéines, dont la plupart sont des enzymes.
Le modèle de structure, représentation schématique de l’objet, ne prend tout son intérêt que s’il permet d’expliquer le mécanisme dans lequel est impliqué l’objet, c’est-à-dire de relier structure et fonction. Des essais, faits dans ce sens, se sont révélés particulièrement intéressants: ainsi, en comparant la structure aux rayons X de l’hémoglobine et de l’oxyhémoglobine, Perutz a mis en évidence un déplacement des chaînes 見 et 廓 par rapport à l’hème. Ce changement, imputable à la fixation de l’oxygène, permet d’expliquer l’effet coopératif des quatre sites de fixation de l’oxygène sur l’hémoglobine.
L’ADN fournit un exemple non moins frappant de ce qu’apporte le modèle structural pour la compréhension d’un processus dynamique. En faisant au départ l’hypothèse «intuitive» que le squelette de la chaîne polynucléotidique était enroulé en hélice, J. D. Watson et F. H. Crick ont abouti, en s’appuyant sur les données physiques (diffraction des rayons X) et chimiques, au modèle à deux brins, de structures complémentaires, enroulés en hélice. L’évidence de cette complémentarité leur a permis d’imaginer un concept tout à fait nouveau pour la réplication du gène: chaque brin sert de matrice pour la synthèse de l’autre (cf. acides NUCLÉIQUES).
L’établissement du modèle de structure primaire, c’est-à-dire l’enchaînement des nucléotides avec l’alternance des quatre bases, a eu une conséquence encore bien plus importante, puisqu’il a permis l’élaboration d’une théorie de la synthèse des protéines [cf. BIOLOGIE MOLÉCULAIRE].
Au niveau des systèmes organisés
Au niveau des systèmes organisés (membranes cellulaires par exemple), les modèles de structure sont encore, plus peut-être que pour les structures moléculaires, susceptibles d’apporter des solutions aux problèmes de fonctionnement [cf. MEMBRANES CELLULAIRES]. Dans ces systèmes, en effet, la structure est d’autant plus compliquée que la fonction à assurer est plus complexe. Les modèles sont réalisés à l’aide de la méthode de diffraction des rayons X, qui permet de déceler des zones de densités électroniques différentes, donc d’établir un modèle de répartition des éléments constitutifs; mais, en outre, la microscopie électronique apporte des informations supplémentaires que l’on ne pouvait obtenir pour les structures moléculaires [cf. MICROSCOPIE].
La réalisation de systèmes plus simples (membranes artificielles) à partir des constituants élémentaires de la membrane fournit des modèles que l’on peut comparer aux membranes naturelles en les soumettant aux mêmes critères expérimentaux.
Modèles physiques
Dans les modèles géométriques, mécaniques ou électriques, la similitude est caractérisée par l’invariance du rapport de certaines grandeurs. Ainsi, une pompe peut être considérée comme un modèle analogue du cœur, lorsque le rapport de certaines grandeurs variables, telles que flux, puissance, pression, est invariant.
Les circuits électriques sont fréquemment utilisés comme modèles analogiques de phénomènes naturels. Depuis longtemps, le nerf a été comparé à un circuit électrique: on peut assimiler chaque portion de membrane de l’axone à un circuit élémentaire de résistance et de capacité variables, aux bornes duquel il existe une force électromotrice, et la fibre tout entière à un câble électrique coaxial (fig. 2). Ce modèle, très généralement admis, appelle cependant quelque réserve, car, dans la transmission de l’influx nerveux, le phènomène est localisé à la surface du nerf, alors que, dans un câble, le courant est conduit dans la masse.
Une autre représentation de la propagation de l’influx nerveux est réalisée par un modèle connu sous le nom de «nerf de Lillie». Sur une barre de fer, passivée, une altération locale de la surface, provoquée par le contact avec une tige de zinc, se propage du point d’excitation jusqu’à l’extrémité. Ce modèle qualitatif constitue un analogue phénoménologique.
Certains systèmes physiques ont pour analogues des systèmes électriques qui, régis par les mêmes lois, sont représentés par les mêmes équations: l’évolution d’une tension élecrique, par exemple, est identique à la variation, au cours d’une cinétique enzymatique, de la concentration d’un substrat en fonction du temps [cf. ENZYMES].
Tous les systèmes biologiques qui mettent en jeu des transports de substance, dans la cellule, d’ions à travers la membrane (réactions enzymatiques multiples) sont représentés par des modèles de ce type.
Modèle de simulation à l’aide d’un ordinateur
Pour rendre compte du fonctionnement d’un système ou du déroulement d’un processus, on établit, à partir de diverses données et en faisant un certain nombre d’hypothèses, un schéma qui traduit la séquence des opérations réactionnelles: c’est l’ensemble des expressions mathématiques du schéma qui constitue le modèle. Les équations reliant les grandeurs variables comportent des paramètres que l’on choisit aussi judicieusement que possible. À partir de ces équations, on calcule au moyen d’un calculateur numérique des valeurs théoriques des grandeurs mesurables qui sont confrontées aux résultats expérimentaux. On vérifie ainsi que le schéma est une bonne représentation du processus. Sinon, on «ajuste» les paramètres, ou même on modifie le schéma jusqu’à ce qu’il rende compte au mieux de l’expérience.
Avec ce type de modèle, on peut simuler des systèmes relativement simples comme des systèmes enzymatiques multiples, mais aussi aborder des problèmes beaucoup plus complexes, comme le métabolisme de la cellule vivante. Un très grand nombre de processus réactionnels, interagissant les uns sur les autres, sont mis en jeu entre un grand nombre d’espèces chimiques (ce nombre peut atteindre près de trois mille dans une cellule d’Escherichia coli ). L’établissement de tels modèles est donc limité par les possibilités de la machine, malgré les simplifications du schéma.
Modèle biocybernétique
Les modèles cybernétiques sont des modèles de simulation de mécanisme de contrôle: ils comprennent donc tous les systèmes artificiels qui simulent le comportement des êtres vivants [cf. AUTOMATE]. On se limitera ici au modèle «biocybernétique», tel qu’il a été défini par A. Fessard [cf. CYBERNÉTIQUE].
Rappelons qu’un système cybernétique comprend une ou plusieurs commandes d’entrée de l’information, une ou plusieurs commandes de sortie, et – ce qui caractérise un tel système – une ou plusieurs boucles de rétroaction avec un organe détecteur et correcteur d’écarts par rapport au programme, qui permet d’agir sur l’entrée (cause) pour modifier ses variations et, dans la plupart des systèmes biologiques, de maintenir un effet constant.
De nombreuses autres fonctions biologiques, que ce soit la régulation de la synthèse des protéines au niveau de la cellule ou les corrélations dans le système nerveux, ou encore la régulation des glandes endocrines, peuvent être simulées par de tels systèmes [cf. HOMÉOSTASIE]. Le modèle est constitué par l’organigramme de cette simulation, qui définit l’ensemble des relations fonctionnelles entre les différents composants du système. Ces composants, représentés par des «compartiments» à une ou plusieurs entrées ou sorties, peuvent être eux-mêmes très complexes, et le système tout entier peut être composé de dizaines de compartiments interconnectés.
Modèle par schéma
Cette revue ne serait pas complète si l’on ne mentionnait pas un modèle d’un type assez particulier, mais très utilisé en biologie, le modèle par schéma ou dessin, qui relève du modèle de structure. Il représente non seulement l’objet ou le système, mais aussi des processus et des mécanismes, à la façon d’un dessin animé. Ce modèle ne représente qu’un aspect très partiel de l’objet, mais il est associé à un code qui, en permettant de l’interpréter, le situe au même niveau que le modèle concret ou même le modèle abstrait.
Qu’apporte à la biologie la notion de modèle? L’utilité d’un modèle concret comme le modèle de structure moléculaire est évidente, car on peut le considérer comme un outil de travail au même titre que des appareils de laboratoire. Ce modèle, en visualisant l’objet non perceptible, permet à l’expérimentateur de vérifier ses résultats, de contrôler ses hypothèses, de proposer, à partir de modèles statiques, des schémas qui rendront compte de processus dynamiques.
En ce qui concerne les modèles théoriques ou modèles abstraits, le développement extraordinaire de ce moyen d’investigation est dû aux nouvelles possibilités du traitement de l’information. Il n’est pour s’en convaincre que de consulter les publications de biologie théorique ou même expérimentale. Établi à partir de l’expérience, étayé par elle, mais la dépassant grâce à des hypothèses nombreuses et simultanées, le modèle théorique peut toujours, à un moment donné de nos connaissances, être remis en question. Il permet de progresser pas à pas dans la résolution des problèmes cernés.
5. Le modèle dans les sciences sociales
Les diverses sciences sociales ont fait dans le passé un usage plus ou moins précoce et font aujourd’hui un usage plus ou moins systématique des modèles mathématiques. Cette circonstance tient à des facteurs divers: traditions des disciplines particulières, formation des chercheurs, implantation institutionnelle des disciplines. Malgré les résistances, on peut dire que le recours aux modèles mathématiques tend à s’étendre et à prendre une importance essentielle dans la plupart des disciplines. Cela est dû pour une part à ce que certains facteurs technologiques conduisent à un accroissement de la demande de modèles, pour une autre part à ce que les modèles mathématiques appliqués aux sciences sociales, d’abord frustes et souvent directement empruntés aux sciences de la nature, font de mieux en mieux la preuve de leur efficacité, pour conférer à ces sciences une discipline et un statut plus rigoureux.
Les premières recherches
Les premières applications des modèles mathématiques à ce qui constitue aujourd’hui le domaine des sciences sociales sont anciennes. Elles remontent pour le moins au XVIIIe siècle, avec les travaux de Buffon sur l’«arithmétique morale», de Condorcet sur la décision des assemblées ou, plus tard, de Cournot sur les décisions des jurys correctionnels. En outre, la statistique mathématique, qui connaît, notamment depuis Laplace, un développement important, s’adresse souvent à des phénomènes relevant des sciences sociales et particulièrement de la démographie, de la sociologie et de la criminologie: les travaux de Ladislaus von Borkiewicz, d’Adolphe Quételet, de Wilhelm Lexis, de Denis Poisson ou de P. F. Verhulst sont au XIXe siècle parmi les plus significatifs de cette tendance.
Les diverses disciplines face aux mathématiques
Malgré la richesse de cette tradition, les modèles mathématiques ne furent pas acceptés avec la même facilité dans tous les domaines. Certes, il est aujourd’hui difficile de prétendre contribuer au développement de disciplines comme l’économie ou la démographie sans une bonne maîtrise du langage mathématique. Mais, en psychologie sociale, en sociologie ou en ethnologie, il n’en va pas de même. Les applications des modèles mathématiques s’y sont sans doute largement développées, notamment depuis la fin de la Seconde Guerre mondiale. Corrélativement, la plupart des universités du monde tendent à imposer l’apprentissage du langage mathématique et statistique aux étudiants en sciences sociales; néanmoins, les résistances demeurent et il reste possible de mener, sans y recourir, d’importantes recherches en ethnologie ou psychologie sociale par exemple.
Cette différence dans la situation de disciplines comme la démographie d’une part et la sociologie de l’autre ne provient probablement pas, comme on l’avance parfois de façon inconsidérée, de ce que l’objet de la seconde est plus complexe que celui de la première. Elle tient plutôt à ce que la sociologie recouvre traditionnellement des problèmes beaucoup plus divers et hétéroclites que la démographie. À cet égard, elle ressemble à l’économie telle qu’on la définissait encore au XVIIIe siècle, antérieurement à la fondation de cette branche de la science économique moderne représentée par des pionniers comme Augustin Cournot, Alfred Marshall, Léon Walras ou Vilfredo Pareto. Ce fait explique en grande partie que les applications des modèles mathématiques soient importantes dans certains secteurs de la sociologie, de la psychologie sociale ou de l’ethnologie, et pratiquement inexistantes dans d’autres.
En psychologie sociale, c’est sans doute l’étude des opinions et des attitudes qui a donné lieu aux efforts de formalisation les plus importants. Les modèles de mesure des attitudes liés à des noms comme ceux de Louis Guttman ou Paul Lazarsfeld doivent être cités à cet égard. En sociologie, l’analyse des organisations, de la mobilité sociale, des décisions politiques ou judiciaires, des situations de compétition ou de conflit, des phénomènes de diffusion et de migration, recourent fréquemment aux modèles mathématiques. En ethnologie, l’analyse des systèmes de parenté dans les sociétés archaïques est sans doute le problème qui, à la suite des travaux de Claude Lévi-Strauss, a donné lieu aux recherches les plus importantes.
L’intuition et l’observation contrôlée
Le développement général des modèles mathématiques dans les sciences sociales est la conséquence de facteurs multiples, mais surtout peut-être du renforcement de la tendance de ces disciplines à s’appuyer sur une observation contrôlée de la réalité sociale. Tant que la sociologie resta surtout spéculative, l’utilité des mathématiques eut du mal à s’imposer. À partir du moment où l’observation se développa, les sciences sociales eurent à traiter des ensembles importants d’informations dont l’analyse impliquait le recours aux modèles mathématiques. Cela contribua à l’élévation, fort lente il est vrai, du niveau de formation mathématique des chercheurs en sciences sociales et, par suite, à une meilleure compréhension de l’utilité d’un tel langage en ce domaine.
Pour un esprit non prévenu, il n’y a aucun doute en effet que ce langage peut fournir aux sciences sociales les mêmes services qu’aux sciences de la nature ou à des sciences humaines telles que l’économie. Son application n’est pas limitée à un type d’objets particuliers. Elle suppose seulement que le problème qu’on cherche à analyser soit défini de manière claire. Si tel est le cas, la formalisation mathématique permet d’aboutir à des déductions auxquelles on ne saurait parvenir à l’aide de la seule intuition. Les travaux de Lévi-Strauss en ethnologie illustrent bien ce point: les systèmes de parenté des sociétés dites archaïques apparaissent étranges à l’observateur qui s’efforce de les comprendre à l’aide de méthodes intuitives; en revanche, la curiosité et l’arbitraire apparents des règles de parenté disparaissent lorsqu’on analyse ces dernières comme des systèmes d’éléments s’impliquant réciproquement. Cela n’est possible que par le recours au langage mathématique. Autre exemple: le problème de la mobilité sociale est aujourd’hui en sociologie un problème à la mode. Mais il est probable qu’on ne maîtrisera complètement les mécanismes de l’ascension, de la stagnation ou de la descente sociale d’une génération à l’autre que lorsqu’on aura développé une théorie des relations gouvernant les variables qui, comme la fécondité différentielle des classes, l’inégalité des chances d’accès à l’enseignement, l’efficacité de l’éducation par rapport au classement social, l’évolution de la structure sociale, de la structure du système d’enseignement, etc., forment un ensemble d’éléments interdépendants qui doit être étudié en tant que tel. Cela n’est probablement pas possible sans recours au langage mathématique.
6. Le modèle en psychologie size=5參
La psychologie élabore des représentations simplifiées de ce qui a pu être appréhendé de la réalité. Quel est le type de données dont on dispose en psychologie? D’une façon générale, ce seront des informations sur le comportement d’un sujet dans une suite de situations dont les caractéristiques sont, du moins en partie, connues. Ainsi, dans une tâche d’apprentissage où l’on veut faire acquérir à un sujet un concept en montrant des objets qui sont ou ne sont pas des exemples du concept, la suite des situations sera la suite des essais de l’expérience, chacun de ces essais étant caractérisé par l’objet présenté et par l’indication qui a été donnée de son appartenance ou de sa non-appartenance au concept. L’information dont on dispose sur le comportement du sujet est la réponse qu’il a donnée: reconnaissance ou non-reconnaissance de l’objet comme exemple du concept. Dans l’investigation clinique, le schéma est le même, mais les informations relatives aux situations ainsi qu’au comportement que le sujet a eu dans ces situations sont à la fois plus riches et moins fidèles, dans la mesure où elles sont constituées en grande partie par des témoignages venant du sujet lui-même ou de l’entourage.
La comparaison des comportements des sujets dans ces conditions fait apparaître des régularités. Ainsi, la présentation d’un objet qui n’est pas un exemple du concept est moins efficace que celle d’un objet exemple, même si l’information apportée dans les deux cas est la même du point de vue logique. En présence de régularités de ce type, qu’on appelle des «faits», le chercheur essaie d’en rendre compte en construisant un système composé d’un ensemble de propositions et capable d’engendrer à titre de conséquences les particularités du comportement dont il doit rendre compte. On rencontre deux types de constructions théoriques appelées les unes théories, les autres modèles. En psychologie, une théorie est un système de propositions qui s’expriment dans le langage habituel et où les déductions font appel seulement à la logique intuitive: telles la théorie freudienne du rêve ou la théorie de Piaget sur la genèse des opérations intellectuelles. On réserve le nom de modèles aux cas où le système est formé de propositions énoncées dans le langage mathématique: alors, la déduction devient purement automatique, qu’elle utilise l’analyse mathématique ou la simulation sur ordinateur; elle permet ainsi de tirer des propositions initiales un ensemble de conséquences infiniment plus riche.
Le contenu
Un modèle doit contenir tous les éléments permettant de déduire ce que sera le comportement du sujet dans un classe donnée de situations: les caractéristiques de ces situations doivent donc y figurer. Ainsi, le modèle comporte d’abord une description formalisée du type de situation auquel il s’applique. Généralement, la situation est constituée par une suite d’essais: chaque essai diffère du suivant, soit par la situation stimulus en présence de laquelle est mis le sujet (type d’objet présenté, temps de présentation, présence ou non d’autres personnes, etc.), soit par le type d’événement qui suit la réponse du sujet et termine l’essai: cet événement peut être l’obtention d’une récompense, le jugement «c’est bien» ou «c’est faux», ou un signal équivalent, ou encore l’absence de toute indication. Le modèle doit comporter cette description schématique de la situation pour être en mesure de fournir directement des prédictions pour cette situation.
Le modèle définit ensuite un ensemble d’éléments hypothétiques, qui sont les états possibles supposés chez le sujet. Ces états représentent les caractéristiques internes du sujet: les seules modifications qui pourront intervenir chez lui, dans le cadre du modèle, sont le passage d’un état à un autre. Les règles selon lesquelles s’opère ce passage sont énoncées dans un ensemble d’axiomes, qui sont les axiomes d’évolution. L’état dans lequel sera le sujet à l’essai suivant dépend en général de son état à l’essai précédent, de la situation stimulus en présence de laquelle il s’est trouvé et de l’événement qui a terminé l’essai. Une dernière catégorie d’axiomes précise comment, dans le modèle, est déterminée la réponse du sujet: ce sont les axiomes de réponse. D’une façon générale, la réponse du sujet dépend du stimulus présenté à l’essai considéré et de l’état du sujet lors de ce même essai.
On peut illustrer ces principes par la description d’un modèle imaginé pour une situation de détection perceptive.
Description de la situation
La situation expérimentale comporte à chaque essai la présentation en vision brève d’un anneau comportant une lacune, que le sujet doit détecter. La lacune peut occuper 40 positions différentes, le milieu de la lacune pouvant être à 5, 15, 25, ..., 395 grades. À la fin de l’essai, l’anneau est montré en vision longue. Cela sera représenté dans le modèle de la façon suivante: l’ensemble des situations stimulus pouvant commencer l’essai est l’ensemble constitué par les 40 nombres de 5 à 395 en allant de 10 en 10; l’ensemble des événements terminant l’essai est également ce même ensemble de 40 nombres, puisque c’est le même anneau avec la lacune à la même position qui est présenté à la fin de l’essai. Soit l’ensemble des stimulus:

Le stimulus à un essai donné n sera appelé sn 捻 S.
Définition de l’ensemble des états du sujet
On suppose qu’à un essai donné, avant la présentation de l’anneau, le sujet attend la lacune à un point donné du cercle qui coïncide avec une position possible de la lacune: c’est son état de préparation.
Soit Z l’ensemble des états de préparation du sujet, cet ensemble est équivalent à l’ensemble S: Z = S.
L’état du sujet à un essai donné n sera représenté par zn 捻 Z.
Axiome d’évolution des états du sujet
On suppose qu’avec une certaine probabilité c le sujet devient préparé à la position où se trouvait la lacune montrée en vision longue à l’essai précédent. En quelque sorte, l’état de préparation du sujet tend à suivre le stimulus, mais avec une certaine inertie. Cela s’écrira:

avec la probabilité c ,

avec la probabilité 1 — c .
Axiomes de réponse
La réponse est déterminée à partir d’un événement hypothétique, qui peut être soit «détection de la lacune», soit «non-détection». Cet événement hypothétique dépend de l’état de préparation du sujet et, d’autre part, du stimulus. Si la lacune apparaît à une position proche de celle où le sujet l’attendait, on suppose qu’il a de plus grandes chances de la détecter. Plus précisément, on suppose que, si la distance entre s et z est inférieure à 100 grades, le sujet a une probabilité faible de détecter la lacune. On appelle dn l’événement «détection» à l’essai n , et 陋n l’événement «non détection», on écrira alors, avec 諸 礪 諸 :
– on a dn avec la probabilité 諸, et 陋n avec la probabilité 1 — 諸 si:

– on a dn avec la probabilité 諸 , et 陋n avec la probabilité 1 — 諸 si:
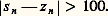
Si l’événement dn se produit, on suppose que le sujet reproduit dans sa réponse la position du stimulus, aux erreurs de reproduction près. Si c’est l’événement 陋n qui se produit, on suppose que le sujet prédit et qu’il donne tantôt la réponse correspondant à son état de préparation, tantôt la réponse correspondant à l’opposé de son état de préparation (intuitivement, le sujet qui n’a pas vu la lacune là où il l’attendait peut penser qu’elle était de l’autre côté). On écrira, rn étant la réponse à l’essai n :
– dans le cas de l’événement dn :

k étant une distribution centrée sur le stimulus sn et symétrique,
– dans le cas de l’événement dn , avec chacun la probabilité 1/2:

En résumé, le processus défini pour le modèle à chaque essai est le suivant: le sujet est dans un certain état de préparation zn (hypothétique); on lui présente un stimulus sn (observable); il se produit l’événement (hypothétique) dn ou 陋n ; il donne sa réponse rn (observable); on lui présente de nouveau sn (observable) en vision longue.
L’estimation des paramètres et la validation du modèle
Il y a dans le modèle un certain nombre de paramètres; ainsi, dans notre exemple: 諸, 諸 , c , la distribution k . Les valeurs de ces paramètres sont estimées à partir de certaines des données de l’expérience. Dans le cas présent, on peut utiliser la courbe des erreurs (différence rn — sn ) obtenue dans une condition où toutes les positions ont la même fréquence d’apparition. Pour cela, on dérive du modèle l’équation qui donne la valeur de cette fonction. Cette équation comporte les paramètres 諸, 諸 , k. On recherche quelles valeurs il faut donner à 諸, 諸 et k pour qu’on obtienne une courbe qui soit aussi voisine que possible de la courbe observée. Cette opération s’appelle l’estimation des paramètres.
Une fois qu’on a obtenu une valeur numérique pour chacun des paramètres, on est en mesure de faire des prédictions relativement à d’autres types de données. Par exemple, dans une situation où le cercle est divisé en trois secteurs, l’un dans lequel la lacune a une fréquence d’apparition forte, les autres dans lesquels cette probabilité est faible, on pourra calculer comment, d’après le modèle, se répartiront les réponses dans les essais où la lacune est dans le premier secteur et dans ceux où elle se trouve dans les deux autres. Pour cela, on déduit à partir des axiomes du modèle l’équation de la courbe des réponses pour chacun des secteurs; on remplace les paramètres de l’équation par leur valeur estimée: on obtient ainsi des courbes théoriques que l’on compare aux courbes observées expérimentalement. Si les courbes théoriques fournissent une approximation satisfaisante des courbes observées, on considère que le modèle est compatible avec les données; sinon, on cherche comment le modifier pour avoir une approximation meilleure.
De l’usage du modèle en psychologie
Le modèle comme approximation
Le modèle est, par définition, une approximation de ce qui est observé. Aussi peut-on dire que, par principe, un modèle est erroné: on pourra toujours montrer qu’il y a un écart entre ce qu’il prédit et les données; cela n’a donc aucun intérêt de montrer qu’un modèle est erroné: on sait a priori qu’il l’est dans une certaine mesure. Le vrai problème est de trouver un modèle meilleur à lui substituer. L’important dans un modèle est qu’il est hautement réfutable: cela est lié à la précision des prédictions qu’il engendre. Par là, il contient le germe de sa réfutation: tel est son principal intérêt, car il permet à la connaissance d’avancer. Une construction théorique n’a de valeur scientifique que dans la mesure où l’on peut préciser quel type de résultat permettrait, si on le constatait, de la réfuter. Bien des théories, on le pressent, ne satisfont pas à ce critère: ce sont les théories trop générales à partir desquelles on peut tout expliquer mais rien prédire.
Modèle et théorie
Un modèle se développe généralement dans le prolongement d’une théorie. Il arrive fréquemment que des théories d’esprit fort différent fournissent des prédictions identiques relativement à une situation donnée. Cela vient de ce que ces prédictions sont seulement qualitatives: dans la situation décrite ci-dessus, deux théories peuvent prédire que les erreurs seront dans l’ensemble moins importantes quand la lacune apparaît dans le secteur à forte probabilité. Il est possible de trancher entre elles. On peut alors essayer d’élaborer à partir de chacune d’elles un modèle qui en conserve les idées essentielles. Ces modèles permettront de faire des prédictions plus fines, en général quantitatives, et par là de tester plus efficacement les théories. En contrepartie de sa simplicité et des possibilités de réfutation qu’il offre, le modèle est en général d’application plus locale qu’une théorie: il s’applique à une gamme plus limitée de situations. Mais cela tient sans doute au niveau de développement de la psychologie. Une discipline qui ne fait qu’accéder au stade scientifique ne possède pas de modèle général: les heuristiques, que constituent les théories, en tiennent lieu.
L’équivalence des modèles
Un des enseignements non négligeables qu’apportent les modèles est la démonstration que deux constructions théoriques partant d’intuitions psychologiques extrêmement différentes peuvent être en fait équivalentes, c’est-à-dire qu’on peut traduire l’un dans l’autre les modèles qui les expriment. Cela signifie qu’il n’y a pas de sens à confronter ces théories, puisqu’elles sont formellement équivalentes et que c’est s’engager dans une impasse que de tenter de le faire. On s’aperçoit, en fait, rétrospectivement qu’un certain nombre de controverses sont nées de problèmes mal posés; la controverse tombe quand les termes du problème sont clairement définis.
L’introduction des modèles en psychologie s’est faite au cours des années soixante. Le bilan de leur apport reste à dresser. On peut dire cependant qu’ils ont permis de poser plus clairement un certain nombre de problèmes dans lesquels la psychologie s’enlisait depuis des décennies. De plus, ils ont largement contribué à orienter les préoccupations des chercheurs vers des phénomènes tels que l’évolution du comportement au cours d’une situation, dont les modèles permettent une analyse fine. Les modèles ramènent ainsi vers l’analyse du comportement individuel la psychologie expérimentale, qui a été centrée essentiellement jusque-là sur l’étude du comportement de groupes de sujets placés dans des conditions comparables; et, de façon assez inattendue, ils retrouvent des préoccupations communes à d’autres approches psychologiques centrées sur l’individu.
7. Le modèle en linguistique
L’activité de modélisation en linguistique a connu un essor considérable depuis le début des années 1970. Comme dans toutes les disciplines qui traitent de données empiriques, les modèles en linguistique cherchent à rendre compte de phénomènes observables: il s’agit de mettre en place un dispositif dont la conception est régie par la théorie linguistique que l’on veut illustrer et dont le fonctionnement produit des résultats comparables aux données observées. La modélisation est donc une manière de mettre en œuvre une théorie, qui permet de mesurer son adéquation aux faits que prétend expliquer cette même théorie. De ce point de vue, plus le modèle est simple, plus son pouvoir explicatif est grand, puisque l’on peut clairement identifier le rôle de chaque élément de la théorie dans son fonctionnement. Mais cet idéal de simplicité est contrebalancé par la nécessité de rendre compte du maximum de données et avec la plus grande précision possible, ce qui réclame en général de complexifier le modèle, et partant de diminuer d’autant sa lisibilité. Il faut donc trouver le meilleur compromis possible entre pouvoir explicatif et fidélité aux données empiriques. Comme dans les autres disciplines, les modèles en linguistique dépendent étroitement des théories dont ils sont issus, et d’abord de la définition des objets d’étude de la discipline. On sait qu’en linguistique, comme dans d’autres sciences humaines, les théories divergent assez vite, y compris sur la nature des phénomènes à étudier: aussi est-il important, quand on cherche à comparer des modèles, de ne pas imputer à la modélisation des qualités ou des faiblesses qui sont le fait des théories sous-jacentes. Comme dans les autres disciplines enfin, ce sont essentiellement les mathématiques qui sont mises à contribution dans l’activité de construction de modèles, soit directement, soit plus fréquemment par l’intermédiaire de l’informatique: en fait, une modélisation informatique dérive toujours d’un modèle mathématique sous-jacent, que cette dérivation soit explicite ou non. Ce rôle important de l’informatique ne doit pas conduire à confondre l’activité de modélisation dont il est question ici et le traitement automatique des langues. Même si des liens étroits se sont noués entre ces deux types d’activité, les objectifs et les méthodes restent différents: pour schématiser, on peut dire que dans le traitement automatique des langues la linguistique doit être en quelque sorte au service de l’informatique, pour aider à accomplir les tâches précises que l’on cherche à automatiser, tandis que dans la modélisation c’est l’informatique qui doit absolument rester sous le contrôle de la théorie linguistique que l’on veut tester.
Au-delà de ces généralités, il faut noter aussi que les modèles linguistiques dans leur ensemble présentent quelques spécificités propres à la discipline. D’abord, le fait qu’il s’agit d’étudier des systèmes de signes permet de différencier deux types de modèles. Les premiers, que nous appellerons modèles internes , cherchent à rendre compte de la combinatoire des signes produits (ou productibles) en elle-même, telle qu’on peut l’observer. Les seconds cherchent au contraire à représenter ce qui fait de ces productions des signes, en traitant de leur relation avec leur forme ou avec leur sens: nous les appellerons modèles d’interface . Comme on le verra, le statut épistémologique des ces deux types de modèles est différent, ce qui doit nous conduire à les distinguer soigneusement, même si une seule et même théorie linguistique peut produire des modèles des deux types ou réduire l’un à l’autre en considérant le langage comme un système clos dans lequel s’intègrent formes et sens des signes linguistiques. Une autre spécificité importante des modèles linguistiques découle du fait que le langage est une activité cognitive humaine, et donc que l’on peut prendre position sur la valeur du modèle en tant que modélisant aussi quelque chose de l’activité cognitive liée à la possession et à l’utilisation du langage: comme on le verra, il s’agit là d’un enjeu important pour les théories linguistiques elles-mêmes.
Les modèles internes
Les modèles de ce type cherchent donc à rendre compte d’observations sur les productions langagières en tant que telles, sans se donner l’objectif de définir ni d’expliquer les conditions (matérielles, biologiques, sociales, etc.) de leur apparition. Il ne s’agit pas d’étudier comment et pourquoi tel ou tel énoncé peut être produit, mais d’expliquer en quoi et pourquoi il constitue bien un énoncé d’une langue. Dans ce type de modèles, la notion d’acceptabilité joue donc un rôle essentiel. Mais cette notion elle-même ne relève pas du modèle: c’est la théorie linguistique qui définit la nature des critères utilisés pour décider de l’acceptabilité ou du rejet d’une production donnée. Une fois ce cadre établi, le rôle du modèle peut être plus ou moins important. Le modèle peut se contenter de représenter les données acceptables en mettant en évidence les structures que la théorie a épinglées: ainsi peut-on dire que les diagrammes syntaxiques qui émaillent les études d’un Tesnière et d’un Martinet sont déjà, en ce sens faible, des modélisations de la syntaxe. Au sens fort, on ne parlera de modèle que si celui-ci est capable de discriminer les données acceptables des données rejetées, ce qui, en principe, permet de tester de manière simple et rigoureuse sa validité: chaque production acceptable que le modèle rejette (et inversement) constitue un contre-exemple qui force à réviser le modèle. C’est ainsi que, toujours en syntaxe, le programme de recherche que s’est fixé Noam Chomsky dès ses premiers travaux consiste à construire «une grammaire générative», c’est-à-dire un modèle de la syntaxe d’une langue qui soit capable d’engendrer tous les énoncés bien formés de cette langue, et rien qu’eux. La popularité de ce programme, qui a complètement transformé le paysage de la recherche en linguistique, est en grande partie due au sentiment qu’il a pu donner, grâce à l’introduction de cette conception des modèles, de transformer la linguistique en une «véritable» science hypothético-déductive, dans laquelle la confrontation de la théorie avec les «faits de langue» pouvait se mener sur une base rigoureuse et parfaitement objective.
Plusieurs remarques s’imposent cependant à ce sujet. D’abord, les faits de langue en question ne sont pas, dans la théorie chomskyenne, des données empiriques. En effet, Chomsky distingue la performance des locuteurs d’une langue, dont relèvent les données empiriques, de leur compétence , qui définit la langue déjà comme un système intériorisé par les locuteurs, auquel ils s’efforcent de se conformer et qui est le véritable objet d’étude de la théorie chomskyenne. Pour ne prendre qu’un exemple de cette discordance théorisée entre la langue et les données empiriques, une propriété essentielle, «basique», des langues serait de pouvoir engendrer un nombre infini de phrases. Cela implique, le lexique étant fini, de pouvoir construire des phrases de longueur non bornée: ce qui, bien sûr, n’est pas le cas des énoncés que peut effectivement produire un locuteur. En fait, la propriété de récursivité qui est invoquée pour justifier cet infini ferait des productions d’une langue un ensemble «inobservable», au même titre que l’ensemble des nombres entiers: paradoxalement, la linguistique est donc dans cette optique une science non expérimentale par son objet même, pour les mêmes raisons que l’arithmétique.
Il faut aussi noter que l’objectif très ambitieux assigné au modèle, à savoir engendrer toutes les phrases d’une langue et seulement elles, puis, plus tard, utiliser un même modèle de base, la «grammaire universelle», paramétrée différemment pour engendrer toutes les langues, n’a jamais été considéré par Chomsky comme forcément réalisable. La position affichée dès le début du programme était de découvrir par ce biais les propriétés les plus intéressantes des langues, et de se focaliser sur celles-ci, alors qu’une approche purement descriptive ne pouvait que se noyer dans la masse des faits, sans pouvoir hiérarchiser l’importance des problèmes à se poser. De fait, il est clair qu’après plus de trente ans de recherches l’objectif que s’était assigné le programme chomskyen est loin d’avoir été atteint, y compris pour la langue la plus étudiée dans ce contexte, l’anglais. Chomsky note lui-même, dans The Minimalist Program (1995), que bien des phénomènes syntaxiques, dont certains assez centraux dans les langues, n’ont pas encore trouvé de traitement satisfaisant, pas même dans les versions les plus récentes de sa théorie. Et s’il est indéniable que ce programme a permis de découvrir, ou de redécouvrir, un grand nombre de problèmes syntaxiques intéressants, on peut se demander si l’accent mis sur ces questions de manière exclusive n’a pas aussi contribué à masquer d’autres problèmes des langues dont l’étude aurait été plus féconde pour la modélisation linguistique en général.
Quoi qu’il en soit, on peut penser que depuis quelques années le programme chomskyen s’éloigne quelque peu de l’idéal d’une modélisation réussie, dans une contradiction permanente entre «un effort vers la simplicité des principes et la nécessité d’incessantes complications et coups de pouce requis par l’adéquation empirique», comme le dit Jean-Claude Milner, qui parle de «dégénérescence» du programme chomskyen en comparant cette situation à celle des dernières versions du modèle de Ptolémée, qui multiplie les épicycles pour sauver la simplicité du principe des déplacements circulaires tout en rendant compte de la complexité du mouvement des planètes.
Cela n’enlève rien au fait que le programme chomskyen a donné une formidable impulsion à la modélisation en linguistique, et particulièrement en syntaxe. Aujourd’hui, un grand nombre de modèles syntaxiques coexistent et se développent, en particulier les grammaires d’unification, sur lesquelles nous reviendrons plus loin. Généralement, ces modèles n’ont plus l’ambition de remplir un objectif aussi radical que celui du programme chomskyen. Il s’agit de couvrir le plus grand nombre possible de phénomènes syntaxiques de telle ou telle langue à l’aide d’un formalisme donné, dans une optique plus classique de modélisation telle qu’on la pratique habituellement dans les sciences expérimentales: on cherche le meilleur compromis entre la simplicité du système et l’adéquation aux faits observables, étant entendu que le modèle ne vise qu’à une approximation de ces données empiriques.
Le fait que nous n’ayons parlé jusqu’à présent que de syntaxe ne doit pas laisser croire que ce serait le seul domaine concerné par ce type de modèles. S’il est vrai que les débats théoriques et épistémologiques se sont centrés sur la syntaxe jusqu’à ces dernières années, la modélisation a touché de fait tous les niveaux traditionnels de l’étude des langues: phonologie, morphologie, syntaxe, sémantique. En particulier, en phonologie (qui a souvent été un domaine précurseur en matière de modélisation), on retrouve toute l’étendue des positions épistémologiques sur la place des modèles que nous avons décrite à propos de la syntaxe, avec une «phonologie générative», qui a joué un rôle analogue de radicalisation théorique, entraînant les mêmes bons et mauvais effets, et avec une profusion actuelle de modèles plus «locaux», s’attaquant à un phénomène précis, comme la syllabation, la position de l’accent ou encore l’intonation.
En sémantique, la situation est plus confuse, parce que l’existence même et l’autonomie d’un niveau de «sémantique linguistique» est loin d’être une évidence: pour certains, qui défendent le primat de la syntaxe, la forme sémantique de l’énoncé est directement issue du modèle syntaxique; pour d’autres, tenants de la pragmatique, la sémantique dépend presque entièrement des conditions de l’énonciation. Dans la mouvance chomskyenne, la lutte a été rude entre les partisans de l’autonomie de modèles sémantiques et les défenseurs plus orthodoxes du respect du primat de la syntaxe. Dans d’autres théories, comme certaines grammaires cognitives américaines (cf. Langacker ou Talmy) et la théorie de l’énonciation d’Antoine Culioli, les relations entre syntaxe et sémantique sont tout autres. Ainsi, pour ce dernier, à chaque marqueur linguistique est associée une opération (décrite par sa «forme schématique»), et ce sont les interactions dynamiques entre ces opérations qui produisent à la fois la structure syntaxique et les effets de sens d’un énoncé: il est clair qu’une modélisation de cette théorie ne peut séparer de manière séquentielle syntaxe et sémantique. Il est donc plus prudent de renoncer pour ce niveau de l’analyse linguistique à un regroupement de modèles issus de théories divergentes. De toute manière, comme on le verra, les difficultés de définition et de représentation du sens (des unités linguistiques aussi bien que des énoncés) rendent plus arbitraire à ce niveau la distinction que l’on a introduite entre modèles internes et modèles d’interface.
Les modèles d’interface
L’ensemble de ces modèles peut à son tour être divisé en deux: d’une part, les modèles qui traitent de l’interface matérielle, c’est-à-dire des relations des signes linguistiques avec leur forme (sonore en général); d’autre part, ceux qui traitent de l’interface conceptuelle, c’est-à-dire des relations avec leur sens.
Du côté de la forme, il s’agit essentiellement de modèles dans le domaine de la phonétique, ou plus précisément à «l’interface» entre la phonétique et la phonologie. Les modélisations les plus intéressantes sont en effet celles qui cherchent à rendre compte des rapports entre la matière sonore et les systèmes phonologiques des langues. On distingue dans ce champ des modèles de production, fondés sur une modélisation de l’appareil phonatoire (le larynx, avec ses cordes vocales, le pharynx et les cavités buccale et nasale), des modèles de reconnaissance, fondés sur une analyse fréquentielle des sons (essentiellement les zones d’harmoniques constituant les premiers «formants» qui permettent de différencier les timbres vocaliques, mais aussi les variations de la fréquence fondamentale), et enfin des modèles «intégrés», qui modélisent la correspondance entre commandes motrices et trajectoires dans l’espace perceptif. Pour ne prendre qu’un exemple typique des questions traitées à ce niveau, on peut chercher à rendre compte avec ces modèles des différents systèmes de voyelles que l’on rencontre dans les langues. En effet, la diversité observée (certaines langues ne possèdent que quatre ou cinq voyelles alors que d’autres en ont beaucoup plus) recèle des régularités remarquables (la position des voyelles dans l’espace «formantique» constitué par les deux premiers formants vocaliques dépend de manière stricte du nombre de voyelles de la langue considérée) dont un modèle peut rendre compte en supposant un principe d’optimisation de la discrimination perceptive par rapport à l’effort phonatoire nécessaire pour les produire (cf. par exemple les travaux de René Carré). Ce qui caractérise ces modèles, c’est qu’il s’agit en fait d’une modélisation qui relève de la physique et dont la problématique est linguistique: il n’est pas si fréquent de rencontrer ce genre de «mixité» entre sciences expérimentales «dures» et sciences humaines... Signalons qu’appartiennent aussi à cette catégorie les modèles de la relation entre les signes des langues de sourds et les mouvements qui les réalisent, ou encore les modèles de la relation entre les signes et leur forme écrite dans les divers systèmes d’écriture (plus particulièrement pour les écritures non alphabétiques).
Du côté du sens, les modèles doivent présenter aussi une sorte de mixité, puisqu’il leur faut à la fois représenter le sens des énoncés, de manière forcément extra-linguistique, et rendre compte du passage de la structure linguistique de ces énoncés à la représentation de leur sens. On observe sur ces deux points une grande diversité, dont on se contentera ici de donner un aperçu à partir de quelques exemples. En ce qui concerne la représentation du sens, on peut relever deux grandes familles: les approches plutôt psychologisantes et les approches plutôt logicistes. Pour les premières, le sens est affaire de cognition, et sa représentation doit donc être de type conceptuel: c’est, par exemple, la position clairement affirmée de Jackendoff, dans le modèle duquel le sens d’un énoncé est représenté par une combinaison de concepts de diverses catégories (objets, substances, événements, processus, etc.). Pour les secondes, le sens est affaire de relation au monde, et sa représentation doit donc donner les conditions qui permettent de décider si cet énoncé est vrai ou faux dans un monde donné. C’est la position qu’a défendue par exemple R. Montague, en développant un modèle dans lequel le sens d’un énoncé est une proposition d’une logique intensionnelle (où, très grossièrement, un prédicat est défini comme une fonction lui associant une valeur de vérité dans chaque monde possible). Il est intéressant de remarquer que l’on rejoint par ce biais la théorie des modèles de la logique mathématique (les «mondes» en question étant essentiellement des constructions ensemblistes, dont le rattachement est problématique, que ce soit au monde vécu ou au monde des physiciens).
La manière dont ces modèles construisent la représentation du sens, quelle que soit sa nature, est aussi très diversifiée. Chez Montague, cette construction est le résultat d’un principe de compositionnalité très strict, qui permet de calculer la forme logique associée à un énoncé à partir de l’arbre issu de l’analyse syntaxique de cet énoncé: à chaque nœud de l’arbre correspond une expression logique calculée récursivement à partir des nœuds-fils et de la relation syntaxique qui les lient. Dans la D.R.T. (Discourse Representation Theory ) de H. Kamp, les règles de construction du sens d’un énoncé font explicitement appel au contexte composé par les énoncés qui le précèdent dans le discours où il est inséré. D’autres modèles, comme la «sémantique situationnelle» de Barwise et Perry, rapprochent plus la sémantique de la pragmatique en prenant en compte d’emblée dans le calcul du sens le contexte en un sens plus large, incluant les conditions d’énonciation (qui parle? quand? où? à qui? pourquoi?). Enfin, comme on l’a vu, il existe aussi des théories pour lesquelles l’analyse syntaxique ne peut être menée indépendamment de la construction du sens, ce qui remet en cause le calcul séquentiel par niveaux (syntaxique puis sémantique) sur lequel sont fondés les modèles classiques.
Les outils mathématiques
Les outils mathématiques les plus utilisés dans la modélisation linguistique sont, sans conteste, de type logico-algébrique. La première impulsion de modélisation des langues en termes algébriques vient sans doute de Zellig Harris (dont Chomsky fut un élève), qui a développé un modèle transformationnel dans lequel les phrases sont obtenues à partir de phrases noyaux subissant une suite de manipulations algébriques. Mais très vite c’est Chomsky lui-même qui assoit définitivement la domination des modèles algébriques en syntaxe avec le programme générativiste. La plupart des modèles syntaxiques qui suivront emprunteront les caractéristiques de base du formalisme chomskyen, en particulier la définition d’une grammaire comme un ensemble de règles de production s’appliquant à un vocabulaire constitué du lexique (vocabulaire terminal) et de symboles désignant les différents types de syntagmes. La suite des règles de réécriture utilisées pour engendrer une phrase peut être symbolisée par un arbre qui fournit donc une représentation équivalente de la structure syntaxique. Des formalismes du même type ont fleuri aussi pour les autres niveaux de l’analyse linguistique: phonologie (dès 1955, dans la thèse de Chomsky), morphologie et sémantique.
Progressivement, ces formalismes ont été remplacés ou transformés par des approches tout aussi algébriques, mais qui se révèlent plus commodes pour la description des unités en termes de traits distinctifs, et plus efficaces pour le traitement automatique: il s’agit des grammaires d’unification, qui sont assez diversifiées mais qui ont en commun d’utiliser un format unique (listes de couples attribut-valeur) pour représenter aussi bien les règles de composition que les structures qu’elles manipulent; le mécanisme qui permet cette homogénéité provient de la technique informatique de l’unification, qui opère en un sens bien précis le regroupement de deux listes de couples attribut-valeur en une seule.
Cette domination des modèles algébriques n’est pas étonnante. Elle est en fait une conséquence directe, au moins pour les modèles internes, du structuralisme tel qu’il s’est imposé, après avoir rompu tout lien avec la Gestalttheorie : définir les unités linguistiques des différents niveaux comme des unités discrètes s’opposant par des traits distinctifs et se combinant pour former des unités de niveau supérieur conduit naturellement à des modèles algébriques. Et cette tendance est confortée par les modèles d’interface avec le sens. Cela va de soi pour les approches logicistes, puisque l’obtention d’une forme logique est facilitée par les représentations algébriques. Mais c’est vrai aussi, en grande partie, pour les approches psychologisantes, puisque le paradigme «computationnel» dominant des sciences cognitives est aussi de type logico-algébrique, qu’il s’agisse du «langage de la pensée» de Jerry Fodor, ou des réseaux sémantiques et autres graphes conceptuels (Sowa).
Il ne faudrait pas en déduire que seules l’algèbre et la logique apportent leur contribution à la modélisation en linguistique. Car les modèles d’interface avec le son font forcément appel aux mathématiques du continu (équations aux dérivées partielles, transformée de Fourier, etc.), tout comme, quoique de manière moins évidente, les autres niveaux de modélisation. En fait, il apparaît assez vite que les langues ne répondent qu’imparfaitement aux critères algébriques de «bonne formation» qui régissent les formalismes classiques. Tant que l’on pense que ces modèles fournissent une première approximation utile des faits, on peut s’en satisfaire. Mais comme le disait dès 1967 Charles Hockett, qui fut l’un des pionniers de ces formalismes algébriques, cela n’est plus possible quand on pense que cette approximation est obtenue en écartant les propriétés des langues qui sont de fait les plus importantes.
Prenons un exemple. La polysémie, cette aptitude des mots les plus courants à avoir une multitude de sens apparentés, distingue radicalement les langues des langages formels utilisés dans ces formalismes algébriques pour représenter le sens. Si l’on pense que la polysémie est une propriété fondamentale de la sémantique des langues, qui explique leur souplesse, leur productivité et leur évolution, on devra renoncer aux modèles algébriques classiques qui conduisent à escamoter ou à marginaliser ce phénomène. Ce sont des raisons de cet ordre qui expliquent que l’on ait pu faire appel aux mathématiques du continu, et plus particulièrement à des modèles topologico-dynamiques en linguistique.
Les travaux de mathématiciens comme René Thom et Jean Petitot, de même que ceux de linguistes comme Antoine Culioli avaient depuis longtemps ouvert cette voie, qui s’est popularisée par la suite, surtout avec l’apparition d’outils informatiques adaptés à la représentation de systèmes dynamiques: les réseaux connexionnistes. Ces nouveaux outils de modélisation doivent aussi en partie leur succès à la facilité avec laquelle ils permettent l’implémentation (ou réalisation) de mécanismes d’apprentissage, qui, comme nous le verrons plus loin, jouent un rôle important dans les relations entre la linguistique et les sciences de la cognition. Signalons aussi l’apparition, encore plus récente, de modèles que l’on pourrait qualifier d’intermédiaires, comme la «théorie de l’optimalité» (A. Prince et P. Smolensky), qui cherche à conserver l’essentiel des qualités des modèles algébriques tout en faisant une place à quelques caractéristiques intéressantes extraites des modèles connexionnistes: très grossièrement, une grammaire est constituée d’un ensemble ordonné, pas forcément consistant, de règles «violables», les énoncés engendrés devant être «optimaux» au sens où ce sont ceux qui violent le minimum de règles de haute priorité.
Modèles linguistiques et cognition
Pour conclure, il nous faut dire quelques mots du rôle de la modélisation en linguistique lors des débats sur la place du langage dans les activités cognitives en général. Les discussions portent principalement sur deux points: d’une part, sur les relations entre l’activité linguistique proprement dite et le reste des activités cognitives liées à la communication langagière, et, d’autre part, sur la problématique de l’apprentissage de la langue maternelle. Dans les deux cas, le type de modèle linguistique utilisé joue un rôle essentiel dans les hypothèses cognitives qui s’affrontent.
Dans le paradigme encore le plus répandu aujourd’hui en sciences cognitives, que l’on appelle généralement le paradigme cognitiviste , défendu entre autres par Jerry Fodor, l’activité linguistique du sujet (comme la perception visuelle et autres activités «périphériques») est une activité automatique, inconsciente et modulaire qui consiste à «traduire» les énoncés de la langue dans le langage computationnel de l’esprit (le «mentalais»), et réciproquement. Cette formulation, que l’on trouve par exemple telle quelle sous la plume du psycholinguiste chomskyen Steven Pinker, est fortement inspirée par les modèles générativistes, qui présentent une architecture compatible avec ce point de vue: ils sont en effet constitués d’un système syntaxique central muni de deux interfaces, qui conduisent l’une à la forme phonétique et l’autre à la forme logique.
S’articule sur ce premier point une théorie de l’apprentissage. La conception chomskyenne d’un système génératif capable d’engendrer une infinité de phrases conduit à un problème sérieux pour l’acquisition par l’enfant de sa langue maternelle, que l’on appelle le problème de la «pauvreté de l’input»: comment l’enfant pourrait-il induire si facilement les règles de bonne formation des phrases de sa langue, alors qu’il n’est soumis qu’à un nombre fini et limité d’exemples de phrases correctes et que ses propres incorrections sont peu (ou même pas du tout) relevées par son entourage? Mathématiquement, on peut montrer qu’un apprentissage de ce type de grammaire ne peut réussir dans ces conditions que si la famille des grammaires possibles est fortement contrainte. Ce qui conduit directement à la thèse «innéiste» chomskyenne: chaque humain naîtrait avec un organe du langage muni d’une grammaire universelle, et l’apprentissage de sa langue maternelle consisterait simplement à fixer un petit nombre de paramètres, à valeur binaire variable suivant les langues. Ce qui, à son tour, sert d’argument à une théorie modulaire de la cognition, dans laquelle cet organe du langage trouve naturellement sa place dans les mécanismes automatiques périphériques. Ainsi des modèles purement linguistiques, «internes», au sens que nous avons donné ici à ce mot, ont-ils des répercussions importantes, bien au-delà des sciences du langage, parfois même contre la volonté de leurs auteurs. Chomsky, par exemple, ne partage pas la conception classique de la modularité telle qu’on la trouve chez Fodor.
À cette conception des relations entre langage et cognition s’opposent d’autres, qui cherchent au contraire à découvrir, à travers l’étude de la diversité des langues, les mécanismes généraux à l’œuvre dans l’activité de langage, lesquels doivent à leur tour aider à mieux appréhender la cognition en général: c’est le programme que s’est fixé la théorie de l’énonciation d’Antoine Culioli, qui utilise largement dans ses formulations des concepts issus de la topologie (ouverts, frontières, etc.) et de la théorie des systèmes dynamiques (attracteurs, bifurcations, etc.). On peut aussi citer, parmi bien d’autres, les grammaires cognitives nord-américaines (Langacker, Talmy, Fauconnier, Lakoff...), dont les analyses linguistiques se fondent sur l’abstraction de schémas perceptifs dynamiques pour rendre compte des phénomènes syntaxico-sémantiques. Dans ces courants aussi, le lien entre langage et cognition passe donc en grande partie par le choix des outils de modélisation des phénomènes linguistiques eux-mêmes. Notons par ailleurs que le problème de l’apprentissage ne se pose plus du tout dans les mêmes termes dans ces approches, puisqu’il n’est plus question d’isoler le processus de bonne formation syntaxique du sens qui est construit par les constituants de l’énoncé: tout l’appareil cognitif de l’enfant peut donc contribuer à l’acquisition de la structure de sa langue.
Ainsi la modélisation en linguistique se trouve-t-elle au centre de débats qui concernent l’ensemble des sciences cognitives, et c’est en grande partie à cette situation que l’on doit la vigueur de cette activité de recherche aujourd’hui.
8. Le modèle en art
Dans le champ théorique qui correspond à l’ensemble des pratiques que l’idéologie rassemble sous la rubrique de l’«art» (au singulier), le mot «modèle» s’entend en plusieurs sens, soit qu’il renvoie à une structure historiquement définie ou à un type d’historicité spécifique, soit qu’il intervienne dans le discours sur l’art au double titre de figure descriptive ou de notion productive.
Le peintre et son modèle
Référée à la structure de renvoi, de redoublement qui caractérise massivement le système de la représentation, la notion de modèle est impliquée d’entrée de jeu dans la définition de la mimèsis , de l’imitation: affirmer que l’art imite la nature (Aristote) revient à signifier qu’il la prend pour modèle, dans ses objets et plus encore dans ses opérations, sinon dans son principe même. Si la perspective sert à démontrer la peinture (idée sur laquelle insistera Léonard de Vinci), c’est dans la mesure où elle se présente moins comme un cours de recettes ou de procédures d’illusion que comme un code régulateur («frein et gouvernail de la peinture»), comme un modèle essentiellement théorique, destiné à rendre raison, en termes spéculaires, de la duplication qui est au principe du système de la représentation. Dans sa transparence feinte, cette construction emporte une série de réductions toujours aléatoires et révocables, toujours menacées au niveau anecdotique – comme on le voit avec Picasso – par les débordements du peintre et l’intrusion sur la toile de la subjectivité aux prises avec le «modèle» et, à un niveau plus théorique, par l’intromission de la surface picturale comme telle dans le circuit spéculaire: réduction du «sujet» de l’énonciation picturale à un œil, sinon à un point (la cuspide de la «pyramide visuelle»); réduction des corps (les objets de l’imitation) à leur enveloppe visible; réduction de la toile ou du panneau au rôle de simple support d’une image dont l’appréhension emporte leur «néantisation» (comme parlent les phénoménologues), en même temps que celle des moyens picturaux, dans leur réalité sensible, leur matérialité spécifique.
Il appartient au projet même de la mimèsis de présenter ses «œuvres» comme le fruit d’un artifice fondé en nature, ce paradoxe visant à oblitérer en elles toute marque du travail, de l’opération dont elles sont le produit. D’où l’insistance (parfois problématique) de la critique classique sur les critères de vérité, de simplicité, de naturel, de justesse, aussi bien que l’importance que prendra, aux limites historiques de la conjoncture définie comme celle de la représentation, la question du modèle vivant . «Mais à quoi tient cette fausseté, demandera Diderot, cela n’est pas dans la nature. Ces gens voient donc d’une façon et font d’une autre» (Salon de 1759 ). Et encore (Salon de 1761 ): «Il y a des passions bien difficiles à rendre; presque jamais on ne les a vues dans la nature. Où est donc le modèle? Où le peintre les trouve-t-il? Qu’est-ce qui me détermine, moi, à prononcer qu’il a trouvé la vérité?» Mais la nature, qu’est-ce à dire, dans un siècle où nul n’est plus accoutumé à la considérer, un siècle qui ne dispose même plus, dans la pratique quotidienne du peintre, de modèles dignes de ce nom? «Nous ne voyons jamais le nu; la religion et le climat s’y opposent [...] Nous ne savons pas ce que c’est que les belles proportions. Ce n’est pas sur une fille prostituée, sur un soldat aux gardes qu’on envoie chercher quatre fois par an, que cette connaissance s’acquiert.»
L’histoire monumentale et ses héros
Il reste que le peintre a d’autres modèles, et ceux-là d’abord que l’histoire lui propose au titre de «chefs-d’œuvre». Le musée fait apparaître la distance existant entre les produits qui ressortissent à l’ordre du goût, de la tradition, et les productions qui prennent figure de modèles efficaces; cette distance, cette efficace définissent un type d’historicité spécifique, fondé moins sur le devenir et la linéarité que sur la discontinuité, la reprise signifiante ou au contraire le refus des exemples du passé, qui, pour appartenir à un temps plus ou moins reculé, n’en produisent pas moins un effet toujours actuel: soit l’espèce d’histoire dénotée par Nietzsche comme «monumentale», laquelle trouve sa contrepartie nécessaire dans l’histoire «antiquaire» qui conserve et qui vénère, autant que dans l’histoire «critique» qui juge et qui condamne.
La notion d’histoire monumentale emprunte de toute évidence à celle de Renaissance , à l’idée d’une époque où l’antichità sera apparue à la fois comme un héritage glorieux et comme le moyen de créer un avenir qui ne le céderait en rien au passé: comme l’a bien vu Erwin Panofsky, la perspective, par la prise de distance qu’elle implique, ne produit pas seulement le cadre de la représentation classique; elle fait le ressort d’une histoire dans laquelle le présent n’apparaît plus comme la suite ou la répétition du passé, mais comme sa reprise, l’invention archéologique doublant l’invention technique qui y trouve sa condition. Parmi les« inventeurs» de la Renaissance, Filippo Brunelleschi occupe une position privilégiée, lui qui aura su produire tout ensemble et le modèle théorique de la construction perspective et le monument inaugural de l’époque: la coupole de Sainte-Marie-de-la-Fleur, structure sans exemple, élevée sans le secours d’aucun échafaudage sur un espace trop vaste pour pouvoir être couvert selon les méthodes traditionnelles, et bien faite pour établir son inventeur en position de héros, au même titre que Giotto ou Uccello, dans une histoire asservie à l’ordre des noms et à l’idée d’une subjectivité productive.
Le modèle architectural
Si la coupole de Brunelleschi a valeur inaugurale, ce n’est pas qu’elle ait emprunté son autorité de la mimèsis , mais dans la mesure où elle apportait à un problème posé de longue date une solution qui en bouleversait les données, fournissant ainsi l’époque d’un modèle inédit. L’architecture est si peu un art d’imitation que le temps viendra où elle paraîtra avoir servi de modèle, par anticipation, au créateur lui-même (le «Dieu architecte» de Kepler): la même puissance de construction est à l’œuvre dans l’univers et dans la science, dont l’œuvre bâtie propose les images, sinon le modèle (et il faudrait s’interroger ici sur la fonction des métaphores architectoniques dans le discours de la science contemporaine, linguistique ou anthropologie structurales, biologie, etc.). Or il n’est pas toujours aisé, s’agissant d’un édifice ou d’une série d’édifices donnés, d’en faire la théorie , ni de décider de la logique qui préside, en l’occurrence, à l’agencement des structures et des formes. Rappelons seulement les discussions auxquelles aura donné lieu le problème de l’ogive, considérée en tant que structure générative de l’édifice gothique ou, au contraire, comme trait stylistique surajouté. La construction gothique a-t-elle son principe dans la croisée d’ogives, l’édifice entier étant pensé, comme le voulait Viollet-le-Duc, par le haut, à partir des voûtes? Obéit-elle au contraire à des impératifs d’ordre tout ensemble fonctionnel et stylistique, qui imposent la réduction au minimum des éléments porteurs, murs et points d’appui, en même temps qu’une délinéation stricte des articulations de la bâtisse? La querelle n’a guère d’objet dès lors qu’on observe que l’analyse structurale, au sens où l’entendent aujourd’hui les grands ingénieurs du bâtiment (Eduardo Torroja, Pier Luigi Nervi, par exemple) – le calcul mathématique appliqué à l’étude des modèles simplifiés des différents types de systèmes mécaniques que met en jeu l’art de bâtir –, ne restitue par définition qu’une image approximative et hypothétique du comportement réel des structures construites. La marge d’inadéquation entre le modèle sur lequel travaille l’analyste et la structure concrète dont il lui appartient de prévoir les réactions, le comportement, cette marge revêt, dans le cas de l’architecture, une signification décisive, puisque, aussi bien, toute structure bâtie, outre qu’elle ne satisfait pas seulement à des fonctions constructives mais sert de support à des développements proprement signifiants, est susceptible de valoir à son tour comme «modèle» à la fois formel et expérimental pour des productions ultérieures. Si même elle n’a pas de fonction mécanique réelle , l’ossature gothique aura fonctionné comme une construction théorique au regard non seulement des archéologues mais des architectes eux-mêmes, s’il est vrai, comme l’a démontré Pol Abraham, qu’elle leur aura fourni un moyen géométrique commode pour établir des voûtes à retombées discontinues, tout en correspondant à la matérialisation dans l’espace du tracé des lignes de pénétration et d’intersection des surfaces.
Modèle et «artefact»
Si toute œuvre d’architecture s’ordonne à un modèle dont il arrive – comme on pourrait le montrer encore à partir de l’ordre classique – qu’elle impose elle-même l’idée sous une espèce visible peut-être inadéquate, partielle, sinon mensongère, la critique à laquelle prête, d’un point de vue théorique, l’épistémologie des modèles ne vaut pas dans un champ qui ne se distribue pas suivant une différence simple entre réalité empirique et formes théoriques: les objets dont il appartient à la théorie de connaître sont eux-mêmes des artefacts , des objets «construits» sinon «bricolés», comme peuvent l’être, à des degrés divers, la maquette offerte à un donateur ou le modèle de la cathédrale «idéale» que Viollet-le-Duc propose en son Dictionnaire . À travers le tracé des voûtes et de leurs retombées, l’édifice gothique produit le modèle empirique de son propre fonctionnement; mais les premières constructions auront fonctionné à leur tour comme autant de modèles techniques, en un sens moins exemplaire que productif. Et la même observation vaut pour une peinture qui ne se veut plus astreinte à l’ordre de la mimèsis et qui n’entend plus connaître d’autres modèles que ses propres produits. Par un renversement des positions logiques, c’est la notion abstraite de «peinture» qui se trouve alors mise à l’épreuve du tableau : un tableau qui n’est plus conçu et exécuté dans sa référence à un modèle extérieur, mais – pour reprendre les termes de Meyer Schapiro rendant compte de La Grande Jatte de Georges Seurat – comme «une suite d’expériences, avec changements continuels de rapports et élimination des perturbations», par interaction continue entre les données de la perception, les idées de la construction et les besoins de l’ordre intérieur du tableau, le tout dans un esprit non seulement rationaliste mais foncièrement théorique . Le moment historique de la rupture peut faire discussion: systématiquement parlant, c’est sans aucun doute la production de Piet Mondrian qui impose le modèle le plus clair et le plus rigoureux d’un retour de «la» peinture sur ses propres constituants, sur ses composantes minimales (surface, ligne, couleur, etc.), modèle dont, pratique ou théorie, l’art contemporain n’a pas encore pris la mesure.
9. Perspective épistémologique
L’usage des modèles, qui sont élaborés naturellement pour les besoins des différentes sciences, pose des problèmes étendus à la logique et à l’épistémologie. La logique est concernée en ce que les modèles donnent matière à l’étude sémantique, qui s’intéresse aux rapports des signes avec la réalité, et à l’étude pragmatique, qui reconnaît les motifs du choix des langages obéissant à des raisons d’efficacité, d’optimalité. Au reste, l’examen des modèles nous fait entrer assez avant dans les conditions de vérité propres aux différentes sciences. Mais la philosophie de la connaissance est concernée aussi, par les témoignages qu’apporte l’emploi des modèles sur les conditions de la compréhension de la recherche et de la preuve, sur la portée du savoir théorique. En fait, la pratique des modèles met en lumière les aspects relatifs et progressifs du savoir et de ses langages; elle est peu compatible avec les conceptions «réalistes» qui supposent que le savoir débouche directement sur l’objet. Elle ne semble pas cependant réclamer les interprétations d’un nominalisme radical, qui ferait s’effacer l’objet devant les procédés de l’expression, car l’aménagement des modèles porte la marque des adaptations à l’objet et des exigences rationnelles d’une adéquation du savoir.
Les fonctions de la modélisation
La philosophie de la connaissance, qui réfléchit sur les procédés de modélisation pratiqués par les différentes sciences, est dans l’obligation d’interpréter une nouvelle fonction, une nouvelle dimension de la rationalité. Les caractères de celle-ci ne sont pas aisés à fixer, parce qu’il s’agit de procédés techniques en voie d’élaboration et parce que la fonction des modèles n’est pas univoque: former des modèles, c’est d’abord dominer par des connexions systématiques les hasards de l’empirie, et ce rôle se remarque surtout dans les sciences qui ont une base descriptive très étendue. Les sciences de la nature et les sciences de l’homme construisent des corps idéaux d’objets, qui, soumis en général au pouvoir d’un langage mathématique, surmontent le détail de l’expérience et neutralisent la part intuitive des conjectures et interprétations. Cependant, le modèle consiste à la fois dans le formulaire symbolique et dans les objets idéaux qui lui sont attachés, et, de cette manière, il donne une base matérielle au concept: il exerce visiblement ce rôle dans les sciences mathématiques, où la liaison de l’équation avec la figuration constitue un complexe intelligible qui donne corps aux opérations déductives. Ainsi, et de manière générale, le modèle s’établit dans une fonction médiatrice vis-à-vis de ce qui est, d’un côté, le plus concret ou, de l’autre, le plus abstrait.
De toute façon, l’emploi des modèles est un adjuvant au service des fins de la connaissance; on aura remarqué que les spécialistes des diverses méthodes de la science parlent des modèles en termes de réalisations «optimales» et qu’ils marquent les rôles mutuellement complémentaires que jouent les modèles: les qualités mêmes auxquelles satisfont les modèles valables sont multiples et reflètent de quelque façon cette diversité des rôles. Ainsi la formation des modèles, au prix de certains artifices, rend possible une simplification, une schématisation des domaines de faits; mais, en même temps, cette transcription permet de totaliser la matière traitée et d’éviter les réductions trop unilatérales. On invente les modèles pour systématiser les points de vue de l’explication; par suite, une certaine rigueur constructive est exigible de ceux-là, mais cette rigueur n’est pas rigidité, car les modèles doivent être adaptables: au sein d’une même science, ils se pluralisent en fonction des propriétés régionales de la réalité qui est à décrire, et ils restent mobiles pour répondre aux conditions de l’invention et de la découverte. Néanmoins, les modèles d’une même science refusent la division, ils tendent le plus possible vers les solutions unifiantes. D’une manière générale, la science est pleinement consciente de cette valeur instrumentale des modèles, elle ne confond pas la vérité signifiée avec les contenus limitatifs de la figuration, elle évite ainsi le dogmatisme qui résulterait d’une confusion de l’objet avec ses modèles. Le modèle est une «fiction surveillée»; celle-ci est contrôlée par les réussites ou les échecs de l’expérience, elle est soumise au critère d’une consistance garantie par la logique ou par la théorie explicative. La modélisation a pour fond la démarche prospective et critique du savoir.
En tout cas, ces contrôles et ces précautions qui accompagnent l’emploi des modèles interdisent au philosophe de leur attribuer les pouvoirs d’une «imagination libre». S’il est vrai que les modèles introduisent dans l’invention scientifique les ressources de l’imagination, il s’agit d’«images liées» et intégrées à l’économie des pensées rationnelles. Ainsi, l’on ne saurait dire que les images de la mécanique classique procèdent directement de la vision épicurienne, préscientifique, du mouvement et du choc des atomes. Ces images se sont assimilé les lois de Huygens concernant la composition géométrique des directions et l’entretien de la quantité de mouvement; elles pénètrent dans le modèle cinétique des gaz, sous le contrôle d’un calcul statistique des vitesses moyennes et sous le signe des équivalences entre l’énergie calorique et l’énergie cinétique représentée par le mouvement des molécules. Le modèle est en fait une projection, dans l’image, des concepts et des lois élaborés par la science.
On remarquera aussi que le modèle comporte tous les états intermédiaires entre une figuration concrète et une détermination abstraite: les grands modèles théoriques sont des composés de la forme figurative et de la forme mathématique. Le modèle de Bohr pour l’atome était bien, à l’origine, tributaire de la figuration orbitale, de l’image géométrique, mais il devient progressivement le moyen d’exprimer les liaisons des éléments énergétiques qui sont définies par les matrices quantiques, lesquelles ordonnent des nombres quantiques bien différenciés. Le facteur essentiel est que les constats empiriques puissent être unifiés, les concepts et arguments théoriques objectivés par des réalisations figurales contrôlées par une forme qui peut être fournie par une géométrie, mais aussi par un calcul algébrique.
C’est cette caractéristique générale que retient un logicien positiviste tel Richard Braithwaite quand il traite les modèles comme des projections de la théorie: l’enchaînement des propositions théoriques qui permettent la prévision ou l’explication de certaines données est matérialisé dans un modèle qui précise le calcul et l’appuie sur des objets fictifs. Ainsi toute l’économie des énoncés scientifiques est dotée d’un support: les énoncés empiriques sont rapportés aux items observables, mais, de leur côté, les énoncés abstraits, les énoncés principes reçoivent le soutien des modèles.
Cependant, lorsqu’il reconnaît ce statut, élaboré et différencié, des modèles, l’épistémologue doit porter son attention sur les fonctions multiples qu’ils exercent. S’il y a avantage à ce que la conception soit ainsi objectivée ou matérialisée, c’est pour plusieurs raisons qui concernent à la fois les intérêts de la compréhension, laquelle bénéficie de la clarté des figures, ceux de la recherche, qui utilise la puissance d’analogie des schémas, ceux même de la preuve, qui trouve dans l’objectivité des modèles une part de ses garanties. Et d’ailleurs, comme ces fonctions se spécifient dans les différentes disciplines scientifiques, selon les objectifs de la recherche et de la preuve qui leur sont propres, il importe de préciser davantage les références des modèles, en s’inspirant des épistémologies particulières.
La sémantique et les modèles en mathématiques
Si l’on s’en tient à une caractérisation très générale des modèles et qu’on entende par là une partie concrète de la théorie qui est directement en rapport avec certains objets, il y a lieu de rappeler que les structures abstraites des mathématiques, définies au niveau des symbolismes purs, se sont formées par abstraction à partir de tels «modèles». Ainsi, la doctrine des opérations numériques a été le point de départ des opérations de l’algèbre abstraite; celle des nombres naturels axiomatisée par Peano a servi de référence à la théorie des ensembles; de même, les échanges entre les procédés de l’algèbre et ceux de la géométrie ont permis le développement des entités vectorielles. Toutefois, c’est par la voie de la «sémantique» moderne que la notion de modèle a pris sa place technique dans la logique mathématique: celle d’un procédé autonome pour la vérification des expressions d’une théorie formelle. La démarche de base est celle de l’«interprétation», ou du choix d’un domaine d’objets avec lesquels on met en correspondance stricte les termes et les énoncés d’un langage symbolique. Deux expressions sont compatibles s’il y a un domaine d’objets où leurs interprétations sont simultanément réalisées; une inférence est invalide si, dans quelque interprétation, les prémisses sont réalisables sans la conclusion, etc. Or un modèle est un interprétant «positif» dont l’existence garantit la consistance d’une théorie: il est naturel de rapporter, à titre de preuve, une théorie qui est en question à une théorie plus fondamentale, dont la vérité ne pourrait être mise en doute sans atteindre le notion même de vérité mathématique.
L’attention a été cependant attirée sur l’importance de cette garantie sémantique par les limites mêmes qu’ont rencontrées les preuves strictement formelles. K. Gödel a établi qu’une théorie ayant au moins la puissance de l’arithmétique ne pouvait être garantie par le langage qui formalise ses expressions. On s’est alors reporté à la définition sémantique de la vérité proposée par A. Tarski, qui s’appuie sur la possibilité de réaliser un formulaire, de conférer une «extension» à ses formules.
Ainsi s’est développée une méthodologie qui repose sur l’interprétation ensembliste des théories logiques et mathématiques et sur les modèles stricts de la théorie des ensembles. D’une part, les entités et les relations de la doctrine des ensembles servent de références à toutes les expressions logiques ou algébriques, et de médiats entre celles-ci et les expressions de la physique et de la mécanique. D’autre part, les constructions ensemblistes sont rapportées à des modèles que valorise la gratuité de leurs lois: modèles arithmétiques, qui permettent la génération récurrente de l’infini; modèles topologiques, qui autorisent des procédés indéfinis de séparation ou de recouvrement. La méthode extensionnelle est, à vrai dire, en concurrence avec des méthodes logiques proprement constructives, mais elle est particulièrement favorable à une extension de la preuve au-delà des limites strictement finitistes.
Considération faite de cet usage logique des modèles dans les démarches de la preuve, il n’est pas interdit à l’épistémologue de prendre la notion de modèle dans un sens plus large: on pensera aux schémas directeurs, qui ont une grande puissance formatrice ou heuristique et autour desquels se forment les théories mathématiques. En ce sens, l’algèbre pourrait être considérée comme «modèle» inspirateur, en raison de la particulière disponibilité de ses chaînes opératoires, ou de la fécondité des extensions qu’elles rendent possibles: à la valeur logique des formes algébriques s’ajoute une valeur pragmatique. On assiste à la naissance d’une doctrine des «catégories», c’est-à-dire des transformations qui assurent le passage d’une structure d’ensemble aux structures de la même famille d’ensembles: or celle-ci met en œuvre les schèmes de l’algèbre en même temps que les ressources de l’intuition géométrique. D’une autre manière, on peut concevoir que la doctrine des ensembles, qui n’a pas été complètement «fondée», est cependant indispensable pour axiomatiser les mathématiques: Gödel a pu la considérer comme une «grande hypothèse» explicative. On le voit, l’épistémologue peut reconnaître la fonction-modèle à la fois dans les réquisits de la preuve et dans les conditions de la création mathématique.
Modèles et réalités dans les sciences exactes
On ne saurait mettre une séparation absolue entre l’usage qui est fait des modèles en mathématiques et celui qu’en font les sciences exactes, qui sont des mathématiques appliquées. D’autant moins que les entités de référence des théories mathématiques, les ensembles numériques ou ponctuels peuvent être pris comme les modèles les plus abstraits des relations physiques: ainsi, quand on réduit les vecteurs et les opérations vectorielles à des multiples de nombres et à leurs produits. Mais les modèles physiques s’échelonnent entre le plan analytique et le plan descriptif; et, surtout, le modèle acquiert ici une fonction expérimentale: il vaut non seulement par sa consistance interne, mais par son adaptation au réel.
Ses fonctions sont d’ailleurs multiples. En illustrant l’enchaînement des propositions d’une théorie, il les rend plus intelligibles, plus disponibles. Mais on peut lui attribuer des rôles heuristiques marqués: il intervient dans la recherche des faits et il étend, de phénomène à phénomène, l’application des lois, ou même il intervient dans la construction des lois nouvelles à partir des lois connues, grâce à la puissance d’analogie qu’il renferme.
Un exemple très simple et déjà ancien illustrera ces possibilités. Les lois expérimentales de Mariotte et de Gay-Lussac, qui relient la pression d’un gaz à son volume ou à sa température absolue, ont été interprétées selon un modèle mécanique: on considère le volume comme la mesure du champ de déplacement des molécules du gaz, la vitesse moyenne des molécules étant régularisée par les lois statistiques et dépendant de l’énergie calorique incluse dans le système, et on explique ainsi les dépendances entre pression, volume et température. Le modèle ainsi construit se généralise expérimentalement. Malgré la différence de la texture d’un liquide et d’un gaz, on peut expliquer la «pression osmotique», exercée par les molécules d’une solution, par des lois isomorphes à celles qui concernent les gaz, lesquelles font intervenir la quantité des molécules et la température. Ou encore, on peut apporter une valeur objective, matérielle, aux grandeurs engagées dans les équations cinétiques et, par exemple, à la masse individuelle des molécules: c’est précisément en comparant la répartition des densités dans l’atmosphère terrestre avec celle qui a lieu dans une «atmosphère miniature» constituée par des gouttes de résine en solution que Jean Perrin a pu évaluer la masse des molécules de l’air. Ou enfin, grâce aux propriétés des «objets» que le modèle adjoint aux lois, celui-ci favorise la synthèse des lois préexistantes: les corpuscules du gaz, qui obéissent aux lois de la mécanique des chocs, sont aussi des «corpuscules newtoniens», soumis à l’attraction mutuelle, et l’on peut concevoir ainsi qu’une compression très grande, par le resserrement des particules, provoque finalement une chute de la pression.
La version positiviste, selon laquelle le modèle est l’illustration «fictive» d’une théorie, ne suffit pas à rendre compte de ces fonctions réalisantes, ou prospectives. Le modèle est un ressort important de cette démarche des sciences rationnelles qui, comme le dit Gaston Bachelard, va de la théorie aux faits en «réalisant» les concepts. Ou bien l’on pourra reconnaître avec Bunge que le modèle, tout en se réglant sur la théorie pour l’exemplifier, s’adjoint à elle pour lui donner une prise technique sur la réalité. On pensera à l’ajustement que réalise le physicien entre les concepts de l’électronique et les modèles concernant le comportement des particules électriques dans une atmosphère qu’elles chargent et dans un champ magnétique qui infléchit leurs trajectoires: ce complexe théorico-figural aboutit aux dispositifs techniques comme ceux de la chambre de Wilson, qui permet le repérage des particules selon leur masse et leur charge, voire la découverte de particules nouvelles, comme c’est le cas des positrons qui ont été détectés de manière expérimentale en même temps que construits pour des raisons mathématiques. Sans le renforcement des modèles, la pensée scientifique serait démunie de l’une de ses fonctions organisatrices, et il importe de remarquer qu’avec leur usage, elle fait plus que coder l’expérience: elle la devance et l’articule.
Modèles et investigation dans les sciences nouvelles
Quelques remarques s’imposent ici sur une méthodologie complexe et en pleine évolution, concernant les sciences neuves, notamment les sciences de la vie, de l’homme, du langage, qui, tant en raison de leur apparition plus tardive qu’en raison de la richesse des faits qu’elles explorent, n’ont pas atteint la précision théorique de la physique ou de la chimie. Certes, leurs problèmes ne diffèrent pas radicalement de ceux que rencontrent ces dernières, et les précédents textes des spécialistes auront montré qu’elles utilisent aussi une multiplicité de modèles: depuis les modèles très concrets qui se tiennent proches de la description des phénomènes jusqu’aux modèles abstraits et mathématiques, lesquels ont pour elles l’intérêt supplémentaire de réprimer les intuitions et les interprétations qui sont une menace pour l’objectivité. Peut-être, cependant, l’état plus prospectif et moins intégré des conceptions des sciences neuves se marque-t-il dans le statut souvent diversifié et concurrentiel de leurs modèles: la pensée recourt à des modèles complémentaires, dont chacun approche une partie de la réalité qui reste un résidu pour les autres modèles. Ainsi, la linguistique s’attache tour à tour aux modèles «structuraux», qui marquent la disjonction et la combinaison des segments du discours, aux modèles «fonctionnels», qui soulignent la dépendance de la texture des messages vis-à-vis des conditions de leur émission ou de leur réception, et aux modèles logico-sémantiques, qui fixent les rapports entre la segmentation du discours et les opérations intellectuelles qui le sous-tendent.
Sans doute cette économie des modèles est-elle liée à un style de la recherche qui s’impose à ces sciences: le modèle est pour elles, comme pour les disciplines plus anciennes, un moyen de réduction et un moyen de prospection, mais en un sens la valeur prospective des modèles, des systématisations qu’ils opèrent, est encore plus marquée. En effet, les sciences traditionnelles ont pu poursuivre progressivement la construction des systèmes explicatifs et l’analyse de l’expérience, tandis que les sciences neuves ont d’abord à articuler des domaines encore non structurés en projetant sur eux des structures définies: ainsi la psychologie de l’apprentissage a abordé les faits sous le signe des modèles mécaniques, cybernétiques, ou des modèles des champs de forces, en les corrigeant les uns par les autres. En outre, les systématisations très larges qui permettent l’explication des faits humains sont quelquefois assez éloignées des systématisations restreintes qui résultent des analyses exactes. L’économiste procède à l’analyse précise des processus de la production et de l’échange, mais il s’inspire des hypothèses plus globales de la sociologie lorsqu’il s’agit d’éclairer les sources et le fondement de la valeur ou des modes du travail.
On suggérera aussi que cette complexité des faits, qui assigne une portée «régionale» aux modèles précis dont se servent les sciences biologiques et humaines, se conjugue avec ce qu’on pourrait appeler l’«implexion» de ces faits: autrement dit, les processus ou les fonctions interfèrent, et, après les avoir différenciés par les modèles appropriés, il est souvent nécessaire de les rapprocher et de les relier par des modèles conjonctifs. Ainsi, la biologie moderne rencontre les régulations de l’organisme à des niveaux multiples: celui des métabolismes, celui des liaisons moléculaires et cellulaires, celui des connexions nerveuses; et la difficulté est de fixer le schéma de fonctionnement qui leur est commun. À l’autre extrémité des sciences de l’homme, la linguistique se trouve devant le problème d’une liaison entre les aspects structuraux, opératoires et génétiques des champs de signes. Le modèles mathématiques de N. Chomsky, conçus pour relier les couches superficielles et les couches profondes de ces champs, paraissent à beaucoup de linguistes encore trop formels pour rendre compte des processus formateurs. Le problème des «codes», c’est-à-dire du contrôle exercé par les formes sur les transformations des matériaux, peut jeter un pont entre les pôles de la biologie et de la linguistique. Mais c’est une confrontation difficile qui s’annonce entre les modèles formés par le généticien et par le linguiste.
Les sciences de l’homme, parce qu’elles sont des sciences neuves, fournissent à la méthodologie de nouveaux témoignages sur l’usage, indispensable et malaisé, des modèles. Mais peut-être leur nature même impose-t-elle de nouvelles conditions à cet usage. Les réalités qu’elles portent à l’objectivité sont elles-mêmes travaillées de l’intérieur par les images et les signes de la vie. Élaborer des modèles logiques et linguistiques de ces réalités, c’est alors en même temps, pour de telles sciences, dévoiler les procédés de signalement, les codages naturels que réalise la vie ou la pensée.
Le rapport de la théorie et de ses modèles
Les fonctions multiples des modèles qu’on vient d’évoquer expliquent certaines divergences de l’épistémologie au sujet de leur statut. La doctrine positiviste est portée à insister de préférence sur les aspects de l’artifice utile ou de l’instrument provisoire. Elle refuse, en effet, les interprétations réalistes de la connaissance: celle-ci est à ses yeux une transcription des données sensibles de l’expérience dans les figures accessibles à l’imagination humaine et dans les formules que choisit le langage déductif, et la modélisation est le procédé majeur de cette transcription. Elle admet, dès lors, que les modèles se succèdent, se remplacent les uns les autres, selon les suggestions de l’expérience et selon les commodités de l’expression. Finalement, par cette voie, on inclut la théorie elle-même dans le procédé de modélisation. Elle ne sera rien de plus que la part logique ou déductive des modèles, à laquelle s’adjoindront des moyens pratiques ou intuitifs de figuration. La connaissance sera sous le signe des codages précis, des conventions utiles: l’existence des modèles fournit ainsi un argument au «conventionnalisme» moderne.
Il peut sembler cependant que l’emploi des modèles est trop engagé dans la prospection des réalités et dans l’approche des vérités pour qu’on réduise son statut à celui des fictions. Cet argument pourrait être formulé par une épistémologie rationaliste sous des formes telles que les suivantes:
– La théorie ne doit pas être confondue totalement avec la somme des modèles sans lesquels elle se fixe provisoirement. Elle apparaît plutôt comme un programme de vérité, orienté par certains concepts directeurs, qui, dans les phases successives de son «remplissement», adopte tel ou tel modèle. Ainsi, la mécanique rationnelle est, depuis ses débuts, l’étude du mouvement des entités réparties dans l’espace sous l’influence des forces et des potentiels qui provoquent et orientent le mouvement. Or, ce programme d’une analyse objective s’est réalisé au cours de l’histoire par des modèles de plus en plus adéquats: tels le modèle cartésien des collisions enchaînées, le modèle newtonien des forces centrales, attractives et répulsives, les modèles de champs qui structurent l’espace et le temps entre les événements. Les bases initiales de la théorie sont révisées par la relativité, qui subordonne les états instantanés aux dimensions de procès, ou par le modèle quantique, qui réduit statistiquement les événements individuels. Ainsi, la théorie se dégage progressivement de ses modèles dans la poursuite de son objectif de détermination.
– Il est insuffisant de dire que les modèles se juxtaposent ou se succèdent, à la manière de formes concurrentes entre lesquelles la science choisirait par convention. En fait, ils sont enchaînés par le dynamisme du savoir, ils se complètent les uns les autres et transitent les uns vers les autres en se transmettant une part des représentations et des formulations qu’ils contiennent. Des événements scientifiques comme la naissance de la mécanique ondulatoire illustrent cet échange des concepts et des formules entre l’image du discontinu et l’image du continu. On a insisté ici même sur la situation complémentaire de nombreux modèles des sciences humaines.
– Lorsqu’on veut clore le modèle sur lui-même, le penser comme une figure complète ou un système fermé d’expressions, on accroît de ce fait sa valeur conventionnelle. Mais, en réalité, les modèles n’ont une signification ni close ni univoque, ils acquièrent de nouvelles dimensions en même temps que la théorie se développe. Ainsi, le modèle structural de l’atome a bien été d’abord une figuration géométrique des orbites, mais il a servi ensuite à condenser les nombres caractéristiques des états de l’électron, d’ailleurs ordonnés par les matrices abstraites de la théorie des quanta: l’image géométrique a perdu sa valeur explicative et ne sert plus qu’à figurer des rapports qui ont un sens strictement énergétique.
Penser le statut des modèles exige beaucoup de précautions de la part de l’épistémologue. Le réaliste y verra des images provisoires de la théorie qui détient le vrai, le relativiste y reconnaîtra les marques des états renversés par une théorie elle-même évolutive. Peut-être le rapport de la théorie et de ses modèles est-il au fond dialectique: la théorie est astreinte à se modéliser, parce qu’elle repart toujours des noyaux d’expérience, des langages qui s’élaborent. Mais elle transcende ces modèles par les orientations stables de la vérification, de l’explication.
Le statut des modèles comme problème métalinguistique
Élucider la fonction des modèles, c’est s’interroger finalement sur le pouvoir de simuler, de figurer, de reproduire, et sur le pouvoir de régulariser ou de normaliser qui appartiennent à la représentation humaine, au langage humain. C’est ainsi qu’en suivant le problème des modèles, on s’oriente vers les fondements d’une métalinguistique, d’une doctrine générale des figures et des signes.
Les travaux de L. Wittgenstein posaient la question et ouvraient déjà plusieurs voies. S’interrogeant sur le rapport du figurant au figuré, du signe au signifié, il nous en donne deux versions successives. L’inspiration du Tractatus logico-philosophicus est logicienne et empiriste à la fois: le mot clé en est celui de «figuration»; il s’agit de la reproduction isomorphique des rapports réels dans les rapports symboliques. Les étages et les types de la figuration: schèmes pratiques, images esthétiques, modèles géométriques ou ensemblistes, laissent apparaître la figuration logique comme la plus abstraite; elle ne concerne plus que le lien de dépendance des faits que l’on affirme. Mais, dans les Investigations philosophiques , conçues dans un esprit plus pragmatique, la perspective change: on admet que l’homme dispose de multiples «jeux de langage» pour décrire, prescrire, calculer, conjecturer, convaincre, etc., et que, chaque fois, les signes visent l’objet par des repérages différents. S’appuyant sur l’image du jeu d’échecs, l’auteur suggère que la connaissance, la «compétence» d’un langage consiste dans une disposition des opérations praticables plutôt que dans la possession de désignations ou de définitions arrêtées.
Or le «relativisme» des logiciens modernes va davantage dans le sens de cette interprétation opératoire que dans celui de l’interprétation figurative. Il n’y a pas de code ultime ou absolu de la reproduction du réel, fût-il logique, mais l’adoption d’un procédé de liaison ou de repérage délimite d’avance la portée des affirmations possibles: il y a rectification des modèles sur leurs applications, plutôt que représentation unifiable. La réflexion métalinguistique conduira à mieux différencier, à assouplir les fonctions régulatrices du langage.
Entre autres, la théorie des langages mathématiques se convainc que ceux-ci n’ont pas de modèle ultime, comme le croyaient les premiers logisticiens. La logique des mathématiques a plutôt pour tâche de prélever, dans le tissu des formules qu’elles produisent, des constructions assez élaborées et formalisées – ainsi l’arithmétique de Peano ou la doctrine des ensembles de Zermelo – pour exercer selon les cas la fonction de modèles. Le domaine des preuves tendra, d’ailleurs, à se répartir entre, d’une part, les modèles pleinement constructifs, mais finitistes, dont les logiques effectives, inspirées de L.E.J. Brouwer, fournissent la règle, et, d’autre part, les paradigmes déductifs, axiomatiques, dont la portée est plus vaste, mais les bases moins établies. Ou encore, les travaux récents d’une logique opératoire ou pragmatique visent à combiner les garanties formelles et les garanties d’efficacité qui intéressent les différents langages de la science: on érigera en règles déductives ceux des procédés opératoires qui se seront révélés les plus aptes à la conduite «stratégique» d’une discussion logique, à la construction récurrente des propositions d’une théorie mathématique ou à la détermination simultanée la plus complète des énoncés de la physique.
Ainsi, la notion des codes ou des modèles se trouve mobilisée en même temps que précisée. Peut-être une évolution analogue se produit-elle dans la doctrine des langues naturelles. Les travaux de la linguistique générative montrent que le code linguistique réalise plusieurs desseins conjugués: traduire le sens dans des expressions patentes, construire une infinité d’expressions sur une base réduite, s’adapter aux besoins renouvelés de la communication des messages. En outre, l’analyse sémantique du langage semble devoir déborder les limites de l’analyse grammaticale: chaque langue particulière, chaque style de l’expression, chaque message apporte avec lui un nouveau «modèle» de l’expression, original bien que conforme aux lois générales de la grammaire. Peut-être cet assouplissement des propriétés du code confirme-t-il les vues de Wittgenstein, qui insistent sur la multiplicité des «jeux de langage».
modelé [ mɔd(ə)le ] n. m.
• 1822; de modeler
1 ♦ Relief des formes tel qu'il est rendu dans une sculpture, un dessin, une peinture. — Par ext. Le modelé du corps.
2 ♦ Géogr. Configuration du relief. Le modelé d'une région.
● modelé nom masculin (de modeler) Relief réel ou simulé des formes en sculpture, en peinture, etc. Aspect que prennent dans le détail les formes du relief terrestre, et dont le façonnement relève de l'action de processus morphogéniques. ● modelé (expressions) nom masculin (de modeler) À modelé continu, en imprimerie, se dit d'un original ou d'un cliché dont les tonalités varient insensiblement du blanc au noir.
modelé
n. m.
d1./d Rendu du relief, des formes, en sculpture, en peinture, en dessin.
d2./d GEOGR Forme ou figuration du relief.
⇒MODELÉ, subst. masc.
A. — BEAUX-ARTS. Rendu du relief, des formes, dans un dessin, une peinture, une sculpture. Cette sculpture, un peu violente, a de bonnes qualités de modelé et de mouvement (DU CAMP, Hollande, 1859, p. 113). Tout le langage du sculpteur tient dans le modelé, c'est-à-dire dans l'art d'utiliser la profondeur, de varier, d'enchaîner, d'équilibrer ses plans, d'organiser ses masses d'ombres et ses masses éclairées (GILLET, Art fr., 1938, p.116):
• ♦ Le Radeau de la Méduse de Géricault, la Barricade de Delacroix, les premières estampes de Daumier portent des traces aussi manifestes des leçons du vieux régicide qui eût reconnu son esprit dans leur modelé montueux où les muscles et le squelette saillent...
FAURE, Hist. art, 1921, p. 162.
— P. anal. Forme harmonieuse, galbe (du corps ou d'une partie du corps). Modelé du visage, des hanches. Eléonore montrait fièrement son cou de neige, sa poitrine et ses épaules d'un modelé délicieux (BALZAC, Modeste Mignon, 1844, p.283). Le regard de ses yeux, le modelé de ses joues (PROUST, Swann, 1913, p.240).
B. — GÉOL. Configuration du relief résultant des différents processus d'érosion. Le modelé amorphe de la Picardie crayeuse (VIDAL DE LA BL., Tabl. géogr. Fr., 1908, p.104).
Prononc.:[ ]. Étymol. et Hist. 1822 Beaux-Arts (DELACROIX, Journal, p. 13); 1868 géomorphol. (LITTRÉ). Part. passé subst. de modeler. Fréq. abs. littér.:325. Fréq. rel. littér.:XIXes.: a) 194, b) 396; XXe s.: a) 424, b) 748.
]. Étymol. et Hist. 1822 Beaux-Arts (DELACROIX, Journal, p. 13); 1868 géomorphol. (LITTRÉ). Part. passé subst. de modeler. Fréq. abs. littér.:325. Fréq. rel. littér.:XIXes.: a) 194, b) 396; XXe s.: a) 424, b) 748.
 ]. Étymol. et Hist. 1822 Beaux-Arts (DELACROIX, Journal, p. 13); 1868 géomorphol. (LITTRÉ). Part. passé subst. de modeler. Fréq. abs. littér.:325. Fréq. rel. littér.:XIXes.: a) 194, b) 396; XXe s.: a) 424, b) 748.
]. Étymol. et Hist. 1822 Beaux-Arts (DELACROIX, Journal, p. 13); 1868 géomorphol. (LITTRÉ). Part. passé subst. de modeler. Fréq. abs. littér.:325. Fréq. rel. littér.:XIXes.: a) 194, b) 396; XXe s.: a) 424, b) 748.
modelé [mɔdle] n. m.
❖
1 (1835). Relief des formes tel qu'il est rendu dans une sculpture, un dessin, une peinture… (→ Arrondir, cit. 5). || Le modelé des surfaces (→ Hachure, cit. 2). || Force, finesse du modelé (→ Importer, cit. 4; masque, cit. 23).
0 Comme modelé et comme pâte, c'est incomparable; l'épaule nue vaut un Corrège.
Baudelaire, Curiosités esthétiques, I, II.
♦ Par ext. || Le modelé du corps.
2 (1868, Littré). Géogr. Configuration du relief (→ Glissement, cit. 6). || Le modelé d'une région.
Encyclopédie Universelle. 2012.