Akademik

ATOME

L’atome est le terme ultime de la division de la matière dans lequel les éléments chimiques conservent leur individualité. C’est la plus petite particule d’un élément qui existe à l’état libre ou combiné. On connaît 89 éléments naturels auxquels s’ajoutent le technétium (Tc, Z = 43), le prométhéum (Pm, Z = 61) ainsi que les transuraniens obtenus artificiellement depuis 1940. Les corps simples sont exclusivement constitués d’atomes identiques; les corps composés sont formés de la réunion d’atomes différents. On appelle molécules des groupements d’atomes caractéristiques de chaque espèce chimique.

L’étymologie renvoie à l’idée assurée jusqu’à la fin du XIX^e siècle que les atomes sont indivisibles. Mais la physique moderne a révélé leur structure complexe à laquelle participent des particules infimes, protons et neutrons groupés dans un noyau, autour duquel se meuvent des électrons . Les dimensions du noyau sont de l’ordre de 10 size=1^漣12 cm, celles des atomes, avec leur cortège électronique, de l’ordre de 10 size=1^漣8 cm.

Deux atomes qui ont le même nombre de protons et d’électrons, mais qui diffèrent par leur nombre de neutrons, ont les mêmes propriétés chimiques, mais leurs propriétés nucléaires sont différentes. Ce sont des isotopes . Un élément préparé par voie chimique est, en général, un mélange d’isotopes qui ne peuvent pas être séparés par des réactions chimiques.

La stabilité d’un système atomique – molécule, atome, noyau – dépend du rapport entre son énergie de liaison et les énergies des processus auxquels il est soumis. Si ces énergies sont beaucoup plus petites que l’énergie de liaison, le système atomique se comporte comme une particule indivisible.

1. Historique

Les origines philosophiques de la notion d’atome

La notion d’atome a été formulée pour la première fois par les philosophes de la Grèce ancienne. On l’attribue à Empédocle, Démocrite, Leucippe, puis Épicure. Leurs conceptions d’une structure atomique de la matière ne procédaient pas d’observations ni d’expériences scientifiques au sens actuel, mais d’intuitions. Leur représentation de l’univers physique était fondée sur l’hypothèse que les corps sont constitués de particules très légères, invisibles et indivisibles. Cette doctrine a été diffusée au I^er siècle avant J.-C. par Lucrèce, dans son De natura rerum. Il y déclare: «Les corps, ce sont d’une part les principes simples des choses, les atomes, et d’autre part les composés, formés par ces éléments premiers. Pour ceux-ci, il n’est aucune force qui puisse les détruire; à toute atteinte leur solidité résiste... Au reste, si l’on n’admet pas dans la nature un dernier terme de petitesse, les corps les plus petits seront composés d’une infinité de parties, puisque chaque moitié aura toujours une moitié et cela à l’infini. Quelle différence y aurait-il alors entre l’univers même et le plus petit corps? On n’en pourrait point établir; car si infiniment étendu qu’on suppose l’univers, les corps les plus petits seraient eux aussi composés d’une infinité de parties. La droite raison se révolte contre cette conséquence et n’admet pas que l’esprit y adhère; aussi faut-il t’avouer vaincu et reconnaître qu’il existe des particules irréductibles à toute division et qui vont jusqu’au dernier degré de la petitesse; et, puisqu’elles existent, tu dois reconnaître aussi qu’elles sont solides et éternelles.»

Atome et chimie

Ce n’est que deux mille ans après ces énoncés qu’une théorie atomique fut scientifiquement formulée. La théorie atomique moderne est née des efforts de Dalton au début du XIX^e siècle pour interpréter les phénomènes quantitatifs de la chimie.

Les notions d’atomes et de molécules se sont imposées pour réunir en une théorie cohérente plusieurs lois expérimentales: loi de la conservation de la masse dans les processus chimiques, de Lavoisier; loi des proportions définies; loi des proportions multiples; loi de Gay-Lussac.

Due à Proust, la loi des proportions définies énonce que les masses des éléments d’un composé chimique sont dans un rapport constant. Si, par exemple, m (H) est la masse de l’atome d’hydrogène, m (O) la masse de l’atome d’oxygène et si la molécule d’eau est constituée de p atomes d’hydrogène et q atomes d’oxygène, la loi de Proust permet d’écrire:

puisque 2,016 grammes d’hydrogène se combinent avec 16 grammes d’oxygène pour produire de l’eau.

La loi des proportions multiples exprime que, si deux éléments sont capables d’entrer en réaction et de former plusieurs composés, les masses d’un de ces éléments qui se combinent à une même masse de l’autre élément sont dans des rapports simples égaux à des fractions rationnelles. L’étude détaillée des composés justiciables de cette loi a permis la détermination des nombres d’atomes, tels que p et q dans la molécule de l’eau.

La loi de Gay-Lussac s’applique uniquement aux corps qui entrent en réaction à l’état gazeux; elle énonce que les volumes des gaz qui réagissent sont dans un rapport simple. C’est ainsi qu’on a déterminé la composition de plusieurs molécules; on a pu montrer, par exemple, que le modèle de Dalton pour la molécule d’eau, HO, n’est pas acceptable; elle est, en fait, formée de deux atomes d’hydrogène et d’un atome d’oxygène.

Pour interpréter les réactions chimiques communes il n’est pas besoin de considérer la structure interne des atomes; les réactions sont décrites par l’échange d’atomes entre les molécules; l’atome a ainsi conservé son caractère de «particule irréductible à toute division» dans les théories chimiques du XIX^e siècle.

Cependant, de nombreux physiciens recourent à une description atomique de la matière pour élaborer la théorie cinétique des gaz et poser les bases de la mécanique statistique classique. On supposait certes que les particules gazeuses obéissaient aux lois de la mécanique de Newton, mais on postulait en outre des lois de nature statistique de sorte que l’ensemble d’un très grand nombre de molécules reproduisît les propriétés macroscopiques des gaz quels que fussent les écarts singuliers. Cette théorie a permis d’évaluer les valeurs moyennes des vitesses moléculaires, les rayons des molécules supposées sphériques ainsi que le nombre de molécules contenues dans une molécule-gramme, nombre intervenant dans la loi d’Avogadro: des volumes égaux de divers gaz, à la même température et à la même pression, contiennent le même nombre de molécules. D’où on infère que la molécule-gramme d’un gaz quelconque contient le même nombre de molécules. On doit à Jean Perrin plusieurs méthodes de détermination expérimentale de ce nombre, dit d’Avogadro, qui est égal à 6,022 憐 10²³. Ces méthodes ont contribué à valider les modèles moléculaires de la matière.

L’atome de Thomson-Lorentz

Ce ne fut qu’à la fin du XIX^e siècle que la notion d’atome comme particule indivisible fut mise en doute. Les expériences sur les décharges électriques dans les gaz raréfiés et l’étude des rayons cathodiques ont amené à la découverte de très légères particules, chargées électriquement, les électrons . Dotés d’une charge négative, la plus petite déterminée expérimentalement jusqu’à nos jours, et d’une masse environ 2 000 fois plus petite que celle de l’atome d’hydrogène, les électrons ont été considérés par Lorentz et Thomson comme des unités composantes de tous les atomes.

La théorie de Lorentz-Thomson était l’aboutissement des beaux travaux de Faraday et de Maxwell qui donnaient une description simple et élégante des phénomènes électromagnétiques; la conclusion la plus importante – liée à la formulation des équations de Maxwell – fut l’identification des ondes lumineuses à des ondes électromagnétiques. La théorie de Maxwell admet que les sources du champ, la densité de charge et la densité de courant sont fonctions données du temps et des coordonnées spatiales. La découverte de l’électron a permis d’introduire une structure granulaire d’unités indivisibles dans le domaine des courants électriques.

La théorie cinétique et la mécanique statistique avaient permis une description des propriétés mécaniques et thermiques des gaz; mais les interactions entre matière et champs électromagnétiques ne pouvaient s’accommoder de l’image d’un atome massif, indivisible, «irréductible à toute division» et électriquement neutre.

L’hypothèse admise par Thomson suivant laquelle les électrons sont animés d’un mouvement vibratoire à l’intérieur des atomes a été développée mathématiquement par Lorentz. Cette théorie fut propre à décrire, pour la première fois, les processus d’émission et d’absorption d’ondes électromagnétiques par les atomes, et notamment la diffusion et la dispersion de la lumière.

L’atome de Rutherford

L’atome, selon Thomson, était constitué de charges positives dont la distribution spatiale la plus simple se déploie sur toute une sphère de rayon égal au rayon atomique, de l’ordre de 10 size=1^漣8 cm d’après les déterminations de la théorie cinétique des gaz. Dans un atome neutre, des électrons seraient enclos dans cette sphère, où ils seraient animés d’un mouvement de vibration, leur charge totale étant égale numériquement à la charge positive de la sphère.

C’est en vue d’étudier la distribution des charges positives dans l’atome que Rutherford et ses collaborateurs ont effectué une série d’expériences capitales. Elles consistèrent dans le bombardement de lames métalliques minces par les particules alpha , d’une source radioactive. La distribution angulaire des particules déviées a montré que les charges positives des atomes de la cible ne pouvaient être présentes dans tout le volume atomique. Les mesures s’accordaient, au contraire, avec leur localisation dans un espace de dimensions linéaires environ 10⁴ fois inférieures à celles de l’atome entier. Cette région constitue le noyau atomique autour duquel doivent se déplacer les électrons soumis à l’action des forces électromagnétiques.

Le modèle de Rutherford identifie la structure de l’atome à un système planétaire; le noyau joue le rôle du soleil, et les électrons celui des planètes. Si ce modèle anéantit l’antique conception de l’atome en tant qu’unité indivisible de la matière, il a cependant opéré une unification radicale: au lieu de 92 atomes tous différents, il représente la matière atomique comme un ensemble de configurations d’électrons et de noyaux.

Influence de la théorie de la relativité et de la théorie des quanta sur la théorie atomique

Cependant que les travaux de Rutherford étaient publiés, deux théories, formulées quelques années auparavant, retenaient l’attention des physiciens: la théorie des quanta de Planck (1901) et la théorie de la relativité d’Einstein (1905). Les travaux de Poincaré, de Lorentz et d’Einstein conduisirent, au début du XX^e siècle, à la découverte d’un énoncé très important, le principe de la relativité ou de l’invariance des lois de la physique par rapport aux transformations du groupe de Poincaré: les lois de la nature sont indépendantes de l’instant et du lieu où se trouve l’observateur; elles sont également indépendantes des directions d’observation dans l’espace et de l’état de mouvement du système de référence pourvu que ce mouvement soit rectiligne et uniforme. Dans la théorie de la relativité, les concepts d’espace et de temps que Newton avait introduits sous la forme d’entités absolues et indépendantes l’une de l’autre sont remplacés par la notion de l’espace-temps, qui définit un univers quadridimensionnel dans lequel se déroulent les phénomènes physiques. Parmi les résultats les plus importants obtenus par Einstein, il importe de noter l’idée que la vitesse de la lumière est la vitesse maximale de propagation des actions physiques; la notion que la masse d’un système quelconque croît avec sa vitesse; l’équivalence entre la masse et l’énergie d’un système physique; la connexion entre champs électriques et magnétiques démontrée par les formules qui transforment ces grandeurs physiques quand on passe d’un référentiel de Lorentz à un autre; et, enfin, la critique de la notion de simultanéité, qui fonde la théorie et institue la notion de covariance par rapport au groupe de Poincaré comme postulat nécessaire dans toute théorie complète des phénomènes atomiques à hautes énergies.

Les applications de la théorie de la relativité à la physique atomique ont été faites beaucoup plus tard, d’abord par Sommerfeld en 1916 dans le modèle atomique de Bohr-Sommerfeld. Mais, en fait, ce fut seulement après 1928, grâce à la découverte par Dirac de l’équation relativiste de l’électron, que le formalisme relativiste a commencé à être utilisé dans la mécanique quantique; et aujourd’hui il est indispensable dans la théorie quantique des champs et dans la physique des particules fondamentales.

Et, pourtant, du point de vue des présupposés de la description physique, la théorie de la relativité n’a pas introduit de changement radical en ce sens que les grandeurs y sont encore représentées par des variables ou des fonctions tensorielles ordinaires, la continuité de ces variables étant retenue comme dans la physique prérelativiste. En fait, les travaux d’Einstein ont constitué le prolongement naturel et l’achèvement de la mécanique newtonienne et de l’électrodynamique de Maxwell (elle-même théorie relativiste). Enfin, la vitesse de la lumière dans le vide a été élevée à la catégorie de constante universelle.

Le premier indice selon lequel la description des processus atomiques exigerait un changement radical des idées issues de la physique classique a été la découverte par Planck, en 1901, d’une nouvelle constante universelle, le quantum d’action h , et des quanta d’énergie. Formulée pour résoudre le problème de la distribution de l’énergie parmi les composantes du rayonnement thermique, la théorie de Planck a reçu, de la part d’Einstein à nouveau, un remarquable développement quand il a montré que la constante h est indispensable à la formalisation de l’effet photo-électrique. D’après Einstein, ce phénomène est explicable si on considère la lumière comme constituée de particules d’énergie, les photons , dont l’énergie est h 益 ( 益 étant la fréquence de la radiation) et la quantité de mouvement est (h 益/c ) ょ ( ょ étant un vecteur unitaire dans la direction de propagation du rayonnement).

L’atome de Bohr

En 1913, Niels Bohr a fait accomplir un pas très important à la physique atomique moderne. Il a montré que la conception quantique introduite par Planck dans l’étude du rayonnement thermique, et par Einstein pour décrire la structure de la lumière, était fondamentale pour tous les phénomènes atomiques.

Le modèle atomique proposé par Ruther-ford ne permettait pas de surmonter une difficulté radicale: si le mouvement des électrons autour du noyau d’un atome était soumis aux lois de la mécanique et de l’électrodynamique classiques, les électrons devaient émettre un rayonnement continu. L’émission d’une radiation de fréquence donnée par un atome devrait s’accompagner des harmoniques supérieurs. Une émission continue de rayonnement serait, en outre, une cause d’instabilité des atomes. Ces supputations théoriques étaient en contradiction avec les données expérimentales recueillies en spectroscopie. Par exemple, l’atome d’hydrogène est stable dans son état fondamental; excité, il émet seulement les radiations dont les fréquences sont déterminées par deux nombres entiers, p et q , d’après la formule de Rydberg:

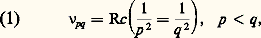
où c est la vitesse de la lumière, et R, la constante de Rydberg: R = 109 737 cm size=1^漣1.

Ces difficultés ont été écartées par Bohr en utilisant la conception quantique de Planck et Einstein. Pour expliquer la relation de Rydberg (1), Bohr a admis les deux postulats suivants:

1. Les trajectoires possibles de l’électron dans l’atome d’hydrogène sont celles dont le moment angulaire est un multiple entier de la constante de Planck divisée par 2 神 ( 領 = h /2 神):

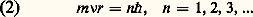
où r est le rayon de la trajectoire supposée circulaire et m est la masse de l’électron. Ce sont les orbites stationnaires ;

2. Quand un électron décrit une orbite stationnaire, l’atome n’émet ni n’absorbe aucun rayonnement. L’émission (ou l’absorption) de radiation est déterminée par le passage de l’électron d’une orbite d’énergie E ^p à une autre orbite d’énergie plus petite (ou plus grande) E ^q , la fréquence du rayonnement émis ou absorbé étant donnée par la relation:

De cette façon, l’énergie du photon émis ou absorbé représente une mesure de la différence entre l’énergie finale et l’énergie initiale de l’atome (fig. 1).

Ces postulats ont donné lieu à deux résultats importants:

– Les trajectoires de l’électron ont des rayons proportionnels au carré des nombres entiers successifs. Cela est une conséquence du postulat 2 et de l’équation de mouvement de l’électron sous l’action d’une force centrifuge m 益²ⁿ /r ⁿ et de l’attraction coulombienne exercée par le noyau Q²/r ²ⁿ :

où Q² = e ²/4 神﨎⁰, e étant la charge de l’électron.

Le résultat à retenir est que l’atome d’hydrogène dans son état fondamental est caractérisé par une longueur, typique de sa structure, le rayon de Bohr a :

qui représente, dans ce modèle, le rayon de l’orbite la plus petite de l’électron dans l’atome.

– La seconde conséquence importante des postulats de Bohr est la formule qui détermine l’énergie de l’atome dans un état quantique défini par le nombre quantique n :

Cette relation est déduite des équations (2), (4), et de l’expression de l’énergie totale de l’électron:

L’équation (6) montre que l’énergie de l’atome d’hydrogène ne varie pas d’une façon continue mais que sa valeur est fixée par le nombre quantique n , puisqu’elle est proportionnelle à 1/n ². L’énergie de l’atome est quantifiée .

L’équation (6) combinée avec l’équation (3) donne la formule de Rydberg où la constante R est exprimée par:

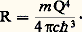
La concordance entre la valeur expérimentale de R et cette expression théorique a été un succès immédiat pour le modèle de Bohr.

Cette description des spectres atomiques a été confirmée par la découverte expérimentale de Franck et Hertz en 1914. En bombardant les atomes d’un gaz par un faisceau d’électrons, ils ont reconnu qu’un atome peut absorber tout ou partie de l’énergie cinétique d’un électron, si elle est égale à la différence des niveaux énergétiques de l’atome, dans les deux états stationnaires final et inital (le tableau 1 donne les diverses grandeurs atomiques).

Atome et mécanique quantique

La période comprise entre 1913 et 1925 est caractérisée par des efforts que déployèrent les théoriciens pour perfectionner le modèle de Bohr. C’est ainsi qu’en 1916 Sommerfeld a pu quantifier le mouvement de Kepler de l’électron dans l’atome d’hydrogène, les orbites de l’électron étant des ellipses dont le noyau atomique est un des foyers. Ces travaux de Sommerfeld furent les premiers à introduire la théorie de la relativité en physique atomique.

Mais le modèle de Bohr-Sommerfeld ne pouvait décrire d’une façon satisfaisante les spectres d’atomes plus complexes que l’hydrogène. Bohr lui-même appelait l’attention des physiciens sur la nécessité de la découverte d’une théorie cohérente des phénomènes atomiques; il soulignait que son modèle était fondé sur une juxtaposition hybride de règles de quantification avec la physique classique qui les ignorait et même les récusait.

La théorie fondamentale de la physique atomique, la mécanique quantique (cf. mécanique QUANTIQUE), fut formulée en 1924-1925, grâce aux recherches de De Broglie, Schrödinger, Heisenberg ainsi que de Born, Jordan et Dirac.

Le point de départ de De Broglie fut l’hypothèse que la dualité onde-corpuscule, établie pour les radiations depuis la conception du photon par Einstein, devait être extensible à la matière.

De Broglie et Schrödinger ont ainsi pu développer un parallélisme entre la mécanique classique et l’optique et parvenir à la conception de la mécanique ondulatoire. Dans cette théorie, l’étude du mouvement d’un électron – ou d’un système atomique quelconque – ne doit pas être fondée sur les trajectoires classiques, solutions des équations de Newton; ce mouvement est décrit par une onde associée à l’électron, l’onde de De Broglie, que définit une fonction complexe des coordonnées d’espace et de temps, 切( ゑ, t ), solution d’une équation aux dérivées partielles, l’équation de Schrödinger:

à laquelle on doit associer des conditions aux limites convenables.

Dans cette équation, l’hamiltonien H est un opérateur linéaire tiré de la fonction hamiltonienne classique, en y remplaçant la quantité de mouvement ら par l’opérateur 漣 i 領 ゞ:

Le point de départ des travaux de Heisenberg a été une critique des notions classiques de position, de vitesse et de trajectoire. Leur application aux systèmes atomiques exige selon lui un critère d’observation et de mesure, qui comporte une limitation et une modification profondes de ces concepts. Il en est résulté l’important postulat suivant lequel les grandeurs physiques doivent être représentées, non plus par des fonctions, mais par des opérateurs linéaires et hermitiques, définis dans l’espace de Hilbert des fonctions d’état (cf. mécanique QUANTIQUE – Formalisme de la mécanique quantique). Les valeurs propres d’un tel opérateur sont des nombres réels et figurent les résultats numériques possibles des mesures de la grandeur physique correspondante. L’impossibilité de la mesure simultanée de deux grandeurs physiques dans un système d’observation donné se traduit mathématiquement par la non-commutativité du produit des opérateurs qui les représentent. On a ainsi construit tout un répertoire d’interprétation physique de l’algèbre des opérateurs linéaires. La relation fondamentale de la mécanique quantique est la relation de commutation:

par laquelle la constante de Planck s’introduit dans l’algèbre de la nouvelle théorie. Les fameuses relations d’incertitude de Heisenberg sont une conséquence de ce commutateur. Selon ce principe, une expérience conçue en vue de manifester avec exactitude la position d’un électron ne permet pas la détermination de sa quantité de mouvement et réciproquement.

La conception du déterminisme classique n’est donc pas recevable en mécanique quantique. Une telle conception implique la possibilité d’une détermination expérimentale précise, au cours d’une même observation, de la position et de la vitesse d’un corpuscule. La connaissance de la position de la vitesse (ou de la quantité de mouvement) d’un corpuscule à un instant donné suffisent alors à déterminer classiquement la trajectoire complète de la particule. La mécanique quantique affirme au contraire qu’une telle détermination est impossible, en raison de la perturbation du système observé introduite par les appareils d’observation. Pour les systèmes macroscopiques mettant en jeu des actions importantes par rapport à la valeur de la constante h , cette perturbation est négligeable et la physique classique conserve toute sa validité.

Schrödinger a démontré l’équivalence du formalisme développé par de Broglie et Schrödinger d’une part, et de celui de Heisenberg, de Born et de Jordan d’autre part. Dès lors la fonction d’onde n’a aucune signification physique propre; elle est un système abstrait opératoire qui représente l’état physique d’un système – elle contient toutes les informations sur celui-ci – et permet le calcul: de la probabilité qu’une variable physique ait une valeur donnée dans une mesure; de la probabilité de transition d’un système physique entre deux états possibles; des valeurs moyennes des grandeurs physiques d’un système dans un état donné.

2. Atome et physique moderne

Atome et lumière

En physique classique, l’émission de rayonnement par un système de particules chargées dépend de l’accélération de ces particules (théorie de Lorenz de l’électron classique). En mécanique quantique, cette image est remplacée par celle de la transition du système d’un état quantique à un autre d’énergie plus petite; cette image décrit correctement les phénomènes observés. Le premier traitement quantitatif précis des processus d’émission et d’absorption de lumière fut proposé par Einstein dans un très beau travail, en 1917. L’état d’équilibre à une température donnée d’un rayonnement enfermé dans une cavité est défini par l’hypothèse que l’énergie rayonnée par les atomes des parois de la cavité est égale à l’énergie qu’ils absorbent pendant le même intervalle de temps. Si un atome est dans un état quantique initial W, avec énergie E^w et s’il est atteint par un photon avec fréquence 益, il peut absorber le photon et passer à un état excité s’il existe un état W de l’atome avec énergie E^w size=1^{, telle que Ew size=1 漣 Ew = h 益. Einstein a postulé que la probabilité d’absorption d’un tel photon est proportionnelle au nombre de photons ayant l’énergie nécessaire h 益 à la transition considérée WW , c’est-à-dire, à l’intensité I( 益, T) de la lumière ayant la fréquence 益, à la température de l’état d’équilibre T. Si nous désignons par P(WW ) la probabilité d’absorption du photon considéré par un atome, par seconde, donnant lieu à la transition de l’état W à l’état W de l’atome, cette probabilité sera proportionnelle à I( 益,T), et le coefficient de proportionalité Bww size=1 est le coefficient d’absorption d’un photon par l’atome et dépend des états initial, W, et final, W :}

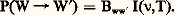
Quand l’atome fait la transition inverse, avec rayonnement d’un photon, de fréquence 益 = (1/h ) (E^w size=1 ^{漣 Ew), il passera de l’état W à l’état W. Planck avait établi en 1901 la loi de distribution de l’énergie entre les composantes d’un tel rayonnement à une température donnée, c’est-à-dire la forme de la fonction I( 益,T). Einstein a découvert que, pour déduire la loi de Planck pour I( 益,T) à partir de l’étude de l’état d’équilibre du rayonnement dans une cavité, il faut considérer que le processus de rayonnement d’un photon résulte de deux mécanismes différents d’émission: l’émission spontanée et l’émission induite (cf. LASERS). Si l’atome se trouve dans un état excité W , il a une probabilité de subir une transition vers un état plus bas, W, même s’il n’y a aucun rayonnement présent: c’est l’émission spontanée. L’émission induite n’a lieu que si l’atome est en présence de rayonnement et est proportionnelle à l’intensité de la lumière avec laquelle l’atome est en interaction. La probabilité d’émission de lumière, avec la transition W W de l’atome sera donc la somme des probabilités d’émission spontanée, Aw size=1w, et d’émission induite, Bw size=1wI( 益,T):}

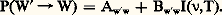
Le nombre d’atomes qui subit la transition WW est évidemment égal au nombre d’atomes n ^w dans l’état W, multiplié par la probabilité P(WW ); le nombre d’atomes dans la transition inverse W W est égal au nombre d’atomes n ^w dans l’état W , multiplié par la probabilité P(W W). L’état d’équilibre du rayonnement dans la cavité est défini par l’égalité des nombres d’atomes qui subissent les deux transitions, par seconde, donc:

Comme la distribution de l’énergie entre les atomes à l’état d’équilibre, respectivement n ^w et n ^w , est donnée par la loi de Boltzmann ^{[cf. STATISTIQUE]}, la loi de Planck se déduira de l’égalité ci-dessus si B^w size=1^{w = Bww size=1 et si le coefficient d’émission spontanée Aw size=1w est proportionnel au coefficient d’absorption et à la troisième puissance de la fréquence 益. La détermination du coefficient Bww size=1 est établie en mécanique quantique par des atomes en interaction avec un champ de rayonnement.}

Si les éléments de la matrice du moment dipolaire de l’atome entre les deux états W et W ne sont pas nuls, l’atome émettra ou absorbera de la lumière (de dipôle) dans la transition considérée entre ces deux états. Il s’agit d’une transition permise . Si, au contraire, ces éléments de la matrice sont nuls, la transition s’appelle une transition interdite . L’intensité de la lumière alors émise est plus faible que celle qui correspond au terme dipolaire d’un facteur de l’ordre de 10 size=1^漣6. Dans ce cas, la radiation est due au moment quadripolaire et au moment magnétique de l’atome. Ces termes sont importants en physique nucléaire, où le système qui interagit avec le rayonnement est le noyau atomique.

L’absorption d’un photon par un atome peut donner lieu à l’émission d’un électron (cf. effet PHOTOÉLECTRIQUE), l’énergie du photon devant être supérieure à l’énergie de liaison d’un électron dans l’atome.

Enfin, remarquons que certains processus d’interaction entre photons et électrons sont importants quand les énergies qui entrent en jeu sont plus grandes (domaine relativiste) que l’énergie de repos de l’électron. Ce sont:

– l’ effet Compton : un photon avec fréquence 益¹ entre en collision avec un électron, qui l’absorbe et recule; un photon est alors émis dans une direction en général différente de celle du photon initial et avec une fréquence plus faible, 益² 麗 益¹;

– l’annihilation d’une paire électron-positron avec émission de deux photons;

– un électron entre en collision avec un noyau atomique et subit une transition vers un état final émergent avec émission d’un photon: c’est le rayonnement de freinage ou Bremsstrahlung .

Une paire électron-positron subit annihilation et donne lieu ensuite, par moyen d’un photon virtuel (intermédiaire), à une paire particule-antiparticule émergente (électron-positron finals, muon-antimuon, hadron-antihadron, etc.).

Les phénomènes d’émission et d’absorption de la lumière par la matière sont donc bien compris; leur étude fait partie de l’électrodynamique quantique et, en général, de la théorie quantique des champs et leurs interactions (cf. effet COMPTON, PARTICULES ÉLÉMENTAIRES, électrodynamique QUANTIQUE).

Atome et spectroscopie

L’étude des spectres des éléments et des corps composés constitue la source essentielle des informations sur la structure quantique des atomes et des molécules. Cette étude repose sur la détermination de la fréquence des raies spectrales qui correspondent à des transitions entre états quantiques, à quoi s’ajoutent la détermination de l’intensité des raies et la considération des règles de sélection qui déterminent les transitions permises et les transitions interdites.

Dans l’équation de Schrödinger d’un atome formé d’un noyau de Z électrons, de charge Ze et de masse M, l’opérateur hamiltonien a la forme:

r ^j étant la distance entre l’électron j et le noyau (r ^j = | ゑ^j 漣 ゑ|), et r ^ij la distance entre les électrons i et j , qui se repoussent mutuellement avec:

Dans le cas le plus simple (celui de l’atome d’hydrogène), cette équation peut être décomposée en deux équations, la première représentant le mouvement libre du centre de masse de l’atome, la seconde:

décrivant la dynamique de l’atome d’hydrogène. Ici, ゑ = ゑ^e 漣 ゑ^p , est la distance de l’électron au proton, 猪 est la masse réduite qui est pratiquement la masse de l’électron.

Dans une équation telle que (8), dont l’hamiltonien possède une symétrie sphérique, on peut séparer la partie de la fonction de Schrödinger qui donne une représentation du groupe des rotations, l’harmonique sphérique Y^lm ( , 﨏) de la partie radiale R^nl (r ) qui dépend du potentiel:

r, , 﨏 sont ici les coordonnées polaires du vecteur ゑ; n , l , m sont trois nombres quantiques tels que:

Eⁿ est l’énergie de l’atome déterminée par le nombre quantique n .

Les nombres l et m déterminent respectivement les valeurs propres des opérateurs qui représentent le carré du moment angulaire orbital de l’électron に:

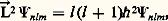
et la composante z de ce moment angulaire:

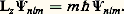
La condition imposée sur la fonction d’état (9), à savoir qu’elle doit être régulière en tout point et convergente quand r 秊, de sorte que l’intégrale:

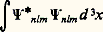
soit finie, détermine l’énergie Eⁿ :

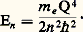
Cette formule est exactement celle (6) qui a été déduite par Bohr au moyen de son modèle, et qui fut vérifiée expérimentalement par Franck et Hertz.

On trouve que l’atome peut subir une transition entre un état défini par les nombres n , l , m et un autre état déterminé par les nombres n , l , m , sous la condition que la variation de l , l = l 漣 l , soit égale à 梁 1 et celle de m , m = m 漣 m , soit 0, + 1 ou 漣 1:

Si les états violent ces règles de sélection, la transition dipolaire sera interdite. Ces règles sont déduites du fait que la possibilité d’émission de lumière est proportionnelle à l’élément de matrice du moment dipolaire, c’est-à-dire à la charge électronique multipliée par une intégrale du type:

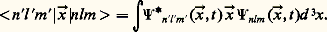
L’intensité de lumière sera essentiellement donnée par ce terme dans l’approximation, dite du dipôle, où la longueur d’onde de la lumière est beaucoup plus grande que les dimensions de l’atome, r ⁰; dans le cas d’émission de lumière visible:

le nombre l est aussi lié à la parité de l’état correspondant, c’est-à-dire à l’opérateur P qui transforme la fonction 切^nlm ( ゑ,t ) en 切^nlm (face=F0019 漣 ゑ,t ):

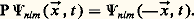
Les valeurs propres de cet opérateur sont précisément de la forme (face=F0019 漣 1)^l ; (face=F0019 漣 1)^l est la parité de l’état 切^nlm . La parité d’un état doit donc changer dans une transition permise (cf. SPECTROSCOPIE - Spectroscopie de l’hydrogène et de l’hélium).

Atome et classification périodique

L’hamiltonien d’un atome à Z électrons peut être écrit sous une forme approximative telle que ses fonctions propres – les orbitales atomiques – soient déterminées par les quatre nombres quantiques de chaque électron A:

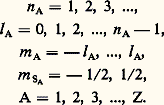
Si un tel atome se trouve à l’état fondamental, tous ses électrons doivent être dans un état dont l’énergie est la plus basse possible. La spectroscopie montre que l’état fondamental d’un grand nombre d’atomes n’est pas un état S dans lequel on aurait n ^A = 1, l ^A = 0 pour tous les électrons A = 1, 2, ..., Z. Ainsi, l’état fondamental de l’atome d’oxygène est ³P², où la lettre P correspond à la valeur L = 2, l’indice inférieur à droite est la valeur de J, l’indice supérieur à gauche indique la multiplicité de l’état: 2 S + 1 (donc S = 1).

Comme l’état ¹S (n = 1, l = 0) est l’état de plus basse énergie dans l’atome d’hydrogène, ce fait indique que dans un atome à plusieurs électrons la distribution obéit à une loi nouvelle qui doit être incorporée à la mécanique quantique. Un autre indice de l’existence d’une telle loi est la périodicité des propriétés chimiques et spectroscopiques des atomes.

C’est pour expliquer tous ces faits que Wolfgang Pauli a formulé en 1925 le principe d’exclusion. Il avait remarqué que l’état fondamental de l’orthohélium n’est pas l’état ³S¹ correspondant aux valeurs des nombres n ¹ et n ² des deux électrons égales à 1. L’analyse spectrale a révélé qu’une propriété semblable était observée pour d’autres atomes, à savoir que certains états permis par la théorie n’existent pas physiquement. Pauli a ainsi découvert que tous les états dans lesquels les quatre nombres quantiques de deux électrons coïncident n’existent pas. Et il a alors donné comme un postulat fondamental pour les électrons, et toutes les particules à spin 1/2, l’énoncé suivant: deux électrons quelconques ne peuvent jamais occuper le même état quantique .

Le principe de Pauli permet d’interpréter la classification périodique des éléments (tabl. 2).

Dans l’approximation des orbitales atomiques, on peut montrer que leurs énergies se rangent en ordre croissant pour les états suivants:

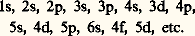
Dans l’atome d’hydrogène (fig. 2) à l’état fondamental, les nombres quantiques de l’électron sont n = 1, l = 0, m ^l = 0 et m ^s peut avoir la valeur 1/2 ou 漣 1/2. Cet état est donc ²S^1/2.

Des deux électrons de l’atome d’hélium (fig. 2), l’un occupe un état analogue à l’état fondamental d’hydrogène. L’autre électron a aussi les mêmes valeurs de n , l , m ; d’après le principe de Pauli, le nombre quantique m ^s du deuxième électron ne peut pas être égal à la valeur correspondante du premier électron. Les deux électrons de l’atome d’hélium auront donc leurs spins antiparallèles. L’état fondamental de cet atome sera donc ¹S⁰, c’est-à-dire un état S (L = 0), avec J = 0, singulet. On indique souvent un tel état par la notation 1s ²: l’exposant indique le nombre d’électrons dans l’état individuel s avec la valeur de n = 1.

L’atome de lithium (fig. 2) contient trois électrons qui se meuvent autour d’un noyau à trois charges positives. Deux de ces électrons forment une configuration analogue à celle de l’atome d’hélium. Selon le principe de Pauli, le troisième électron ne pourra pas avoir son nombre quantique principal n = 1. La valeur de n ³ sera n ³ = 2. Par conséquent, l ³ peut être égal à 0 ou 1: l ³ = 0,1. L’expérience seule peut indiquer laquelle de ces deux valeurs est à retenir. Comme l’on a trouvé que l’état fondamental du lithium est ²S^1/2, il s’ensuit que le troisième électron occupe l’état 2s.

La valeur de n = 1 détermine ce qu’on appelle la couche K , qui est saturée par deux électrons. La valeur n = 2 détermine la couche L saturée par huit électrons, car si n = 2, on aura deux électrons avec l = 0, m ^l = 0 et m ^s = 1/2 ou 漣 1/2, et six électrons avec l = 1, m ^l = 1, 0, 漣 1, chacun desquels aura les deux valeurs possibles de m ^s . C’est le cas du néon qui est constitué de dix électrons disposés d’après la figure 3. Il est dès lors évident que le néon a des propriétés semblables à celles de l’hélium. La configuration du néon est 1s² 2s² 2p⁶.

On voit que le principe de Pauli oblige le onzième électron de l’atome de sodium, élément qui suit le néon, à occuper la couche 3s. Cet électron détermine la valence de l’élément; le sodium, le potassium sont monovalents comme l’hydrogène.

La structure électronique des atomes est donnée dans le tableau 3. La similitude de structure de deux atomes donne lieu à la similitude des propriétés chimiques et spectroscopiques des éléments correspondants.

Il y a enfin lieu de noter que le principe de Pauli introduit en mécanique quantique l’exigence que la fonction d’onde de n électrons soit antisymétrique par rapport à l’échange des variables d’espace et de spin de ces particules.

Atomes et forces atomiques

Tous les atomes et molécules neutres, suffisamment éloignés l’un de l’autre, s’attirent avec une force dont l’énergie potentielle varie comme l’inverse de la sixième puissance de la distance mutuelle. Ce sont les forces d’attraction de Van der Waals , responsables de la cohésion des atomes des liquides ou des gaz rares solidifiés, par exemple dans les cristaux moléculaires d’hydrogène solide.

Ces forces résultent de l’action que le système de charges d’un atome ou molécule neutre produit sur celui d’un autre atome ou molécule. La théorie classique a permis une description intuitive des forces d’attraction de Van der Waals; on a ainsi classé ces interactions en différents types:

a ) attraction «dipôle-dipôle», qui agit entre les molécules polaires (possédant un moment électrique dipolaire permanent);

b ) attraction «polarisabilité-polarisabilité», entre les atomes et les molécules neutres et symétriques, c’est-à-dire homopolaires;

c ) attraction «dipôle-polarisabilité», entre une molécule polaire et un atome sphériquement symétrique.

La théorie complète de ces forces a été formulée en mécanique quantique. Un modèle simple du système des forces de Van der Waals a été développé à cet égard par London. Cet auteur a étudié les forces qui se produisent entre deux oscillateurs linéaires constitués chacun d’une charge négative vibrant autour d’une charge positive très lourde elle-même en repos. Pour des distances entre les centres des deux oscillateurs, R, très grandes en comparaison avec les dimensions de chaque oscillateur, il apparaît que l’énergie du système se compose de la somme des énergies du point zéro des deux oscillateurs et d’un terme additionnel négatif et inversement proportionnel à la sixième puissance de R.

Quand il y a superposition des nuages de charge de deux systèmes atomiques, des forces d’un autre type entrent en action. Dans le cas de deux couches atomiques saturées, fermées, dans le sens du principe de Pauli, qui se superposent, une force de répulsion très intense apparaît: c’est la force de répulsion moléculaire dont l’énergie potentielle, sous la forme dite de Lennard-Jones, pour les molécules sphériques, varie comme l’inverse de la puissance onzième de la distance intermoléculaire.

En raison de l’action des forces d’attraction et de répulsion de Van der Waals, l’énergie potentielle de molécules sphériques est représentée par la courbe de la figure 4, en fonction de la distance moléculaire.

Quand les fonctions d’onde de deux atomes (à couches électroniques non saturées) entrent en superposition, un autre type de forces agit entre les deux systèmes: ce sont les forces de liaison chimique .

La liaison chimique homopolaire est déterminée par une paire d’électrons tels que chacun de ces corpuscules peut être regardé comme appartenant aux deux systèmes; si l’énergie du système formé est plus petite que la somme des énergies des deux atomes séparés, le couple d’électrons donnera lieu à une molécule stable. L’exemple le plus simple est celui de la molécule d’hydrogène (fig. 5). Si deux atomes A et B sont très éloignés l’un de l’autre, on peut envisager isolément chacun des électrons de ces atomes. Quand les deux atomes sont très proches, un quelconque de ces deux électrons est attiré non seulement par le noyau de l’atome A mais aussi par celui de l’atome B. On peut alors montrer qu’un tel système peut avoir deux états; un de ces états, l’état de liaison chimique, possède une énergie qui présente un minimum quand on fait varier la distance entre les deux noyaux A et B. Dans cet état, les deux électrons sont couplés de telle façon que leurs spins sont antiparallèles. On dit que ces spins sont saturés. De cette façon, l’on comprend la définition de la valence d’un atome ou d’une molécule comme le nombre d’électrons dont le spin n’est pas saturé. C’est pourquoi les gaz rares ont une valence nulle.

En plus de la liaison chimique homopolaire – qui ne peut pas être expliquée par la physique classique – il faut considérer aussi les forces de liaison hétéropolaire. Ces forces se manifestent dans les cristaux ioniques dont le réseau cristallin est constitué d’ions métalliques, positifs et d’ions métalloïdiques, négatifs, comme celui du chlorure de sodium. Le réseau est alors l’expression d’un équilibre où jouent des forces d’attraction électrostatique entre les deux types d’ions et des forces de répulsion de Van der Waals (en plus des forces d’échange).

Atome et théorie du solide

La théorie atomique et les méthodes de la mécanique quantique ont permis une description détaillée des propriétés de la matière à l’état solide (cf. physique des SOLIDES).

Les cristaux sont caractérisés par un arrangement très ordonné de leurs atomes tel qu’un réseau géométrique caractéristique se répète dans tout le cristal (fig. 6).

Les corps amorphes sont constitués d’atomes qui ne sont que localement ordonnés. Un réseau d’atomes se prolonge dans un autre réseau un peu différent du premier.

Les principaux solides cristallins se classent, en général, dans les types suivants:

1. Les métaux et alliages métalliques; les forces d’interaction responsables du maintien des atomes dans les réseaux métalliques sont nommées forces de liaison métallique. Les atomes dans le métal ont un électron qui n’est pas très fortement lié; il en résulte que celui-ci peut migrer aisément d’un atome à l’autre, ce qui explique les propriétés de conductions électrique et thermique des métaux. Le gaz que formeraient de tels électrons obéit au principe de Pauli; il est décrit par une théorie statistique due à Fermi et Dirac.

2. Les cristaux ioniques: les nœuds du réseau sont occupés par des ions.

3. Les cristaux moléculaires incluent des atomes ou molécules neutres dans leurs réseaux. Les forces de liaison entre ces atomes ou molécules sont les forces d’attraction de Van der Waals.

4. Les cristaux de valence sont constitués d’atomes dont les interactions sont des forces de liaison chimique (diamant); le couplage correspondant des électrons explique la grande résistance électrique de ces cristaux.

5. Les semi-conducteurs dont les propriétés résultent, en général, de la libération d’électrons par des impuretés insérées dans un réseau cristallin, avec mise en œuvre d’une énergie faible par rapport à l’énergie d’excitation d’un atome libre, énergie qui n’est pas très grande non plus en comparaison avec l’énergie thermique k T.

6. Les cristaux à liaison hydrogène, pour lesquels la cohésion est créée par le déplacement d’atomes d’hydrogène d’un radical vers la partie négative d’une autre molécule.

3. Atomes et particules élémentaires

Positron et antiparticules

La mécanique quantique non relativiste est en mesure de donner une explication et une description détaillée des propriétés chimiques des atomes et molécules. Elle n’est pas capable de décrire les phénomènes atomiques à hautes énergies, c’est-à-dire les processus qui mettent en jeu des énergies supérieures à l’énergie de repos des particules du système.

Dans ces processus, il peut y avoir création aussi bien qu’annihilation et transmutation de particules. La théorie quantique des champs permettant de comprendre ces phénomènes a débuté avec la découverte des équations quantiques relativistes des particules libres (cf. mécanique QUANTIQUE). La première de ces équations, découverte en 1926 indépendamment par de Broglie, Schrödinger, O. Klein et W. Gordon, est l’équation dite de Klein-Gordon:

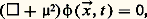
où « 撚 » est l’opérateur d’alembertien donné par 撚 = (1/c ²)(face=F0019 煉²/ 煉t ²) 漣 et 猪 = (m ⁰c )/ 寮 est la longueur d’onde Compton de la particule avec masse m ⁰. Elle s’obtient de la relation relativiste entre énergie et impulsion:

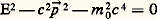
par la substitution de ces grandeurs par les opérateurs correspondants:

et l’application de l’opérateur résultant sur une fonction des coordonnées et du temps 﨏( ゑ,t ). Cette fonction est un champ qui décrit les particules massives à spin zéro, scalaires ou pseudoscalaires.

L’équation quantique relativiste de l’électron (et des particules avec spin 1/2) a été découverte par Dirac en 1928. Au moyen de cette équation, appliquée à l’électron de l’atome d’hydrogène, on obtient la formule de Sommerfeld pour les niveaux d’énergie de cet atome. Elle permet également la description «naturelle» du spin de l’électron et du magnéton de Bohr associé; en plus elle est en accord, dans l’approximation non relativiste, avec la description phénoménologique du spin imaginée par Pauli en remplaçant la fonction de Schrödinger par une paire de fonctions d’ondes complexes, le spineur de Pauli. L’entité mathématique qui correspond, dans la théorie de Dirac, à la fonction de Schrödinger est un spineur à quatre composantes, une paire de spineurs à deux composantes, défini par une certaine loi de transformation sous le groupe de Poincaré et qui est le champ des corpuscules avec spin 1/2. L’équation de Dirac admet deux solutions qui décrivent un électron avec impulsion ら et énergie positive E = c ( ら² + m ²⁰c ²)^1/2 et qui correspondent aux deux valeurs possibles, 1/2 領 et 漣 1/2 領 , d’une des composantes de son spin. Mais elle admet également et nécessairement pour un tel électron avec impulsion ら, deux autres solutions avec énergie négative E = 漣c (p ² + m ²⁰c ²)^1/2 et qui correspondent aux deux états de spin mentionnés. On conçoit difficilement ce que peut être un corpuscule libre à énergie négative : en l’état de repos sa masse serait négative et sous l’action du champ de gravité une telle particule se déplacerait en opposition à la force, cela n’a pas été observé jusqu’à aujourd’hui. Comme les solutions à énergie négative de l’équation de Dirac sont nécessaires pour exprimer une solution quelconque de cette équation en une base complète, Dirac a fait appel au principe de Pauli pour poser une définition astucieuse du «vide». Le «vide» est considéré comme l’état dans lequel tous les niveaux à énergie négative sont occupés – un électron dans chaque niveau – et les niveaux à énergie positive sont vides. Les électrons à énergie négative ne sont pas observables. Mais une interaction extérieure (photon, électron libre) peut provoquer une transition d’un électron d’un état à énergie négative (inobservable) à un état d’énergie positive (observable). Cette transition laisse une lacune dans le vide et on peut montrer que ce «trou» se comporte comme une particule (observable) de même masse que l’électron mais avec une charge positive; elle s’appelle positron ou anti-électron . Ce raisonnement de Dirac fait appel à un ensemble infini d’électrons et son traitement rigoureux est l’objet de la théorie quantique des champs où Feyman a postulé qu’un corpuscule à spin 1/2 avec charge e et énergie négative qui se déplace vers le passé (inobservable) est équivalent à un anticorpuscule avec charge 漣 e et énergie positive qui se déplace vers le futur (observable). Tous les corpuscules à spin demi-entier ont un anticorpuscule. La création d’une paire électron-positron correspond à la transition décrite en haut; la réaction inverse est l’annihilation électron-positron dont l’énergie se transforme en celle de photons.

Fermions et bosons

Après la découverte (Chadwick) du neutron ^{[cf. NEUTRON]} en 1932, qui a résolu le problème de la constitution des noyaux atomiques ^{[cf. NOYAU ATOMIQUE]}, les mésons pi (pions) et les muons ont été découverts en 1947 par Lattes, Occhialini et Powell. Tandis que les pions (positifs, négatifs et neutres) ont spin zéro et une masse égale à 270 fois celle de l’électron, les muons (négatifs) et leurs antimuons (positifs) ont spin 1/2 et une masse égale à 212 m ^e .

À partir des années 1950, beaucoup d’autres particules ont été trouvées expérimentalement. On connaît aujourd’hui plusieurs dizaines de ces corpuscules qui se classifient en fermions (particules avec spin demi-entier) et bosons (particules avec spin zéro ou entier).

Leptons et hadrons

Une particule, prédite par Pauli (1933) avec spin 1/2 et masse nulle, le neutrino 益^e (neutrino électronique), accompagne l’électron dans la désintégration radioactive du neutron ^{[cf. NEUTRINOS]}. On a trouvé qu’un autre neutrino, le neutrino muonique, 益 size=1^猪, est associé aux muons 猪, et un troisième neutrino est actuellement postulé, le neutrino tauonique 益 size=1^精, qui doit accompagner le tauon 精, particule chargée à spin 1/2 avec une masse d’environ 3 490 m ^e . L’électron, le muon et le tauon et leurs neutrinos respectifs constituent une classe de particules, appelée leptons , qui subissent des interactions faibles (telles que celles qui donnent lieu à la radioactivité bêta), électromagnétiques et gravitationnelles . En plus de ces trois types d’interactions physiques fondamentales, il y a un quatrième type d’interaction, les interactions fortes , comme celles qui existent entre les neutrons et les protons des noyaux atomiques. Les leptons ne subissent pas d’interactions fortes.

Par opposition aux leptons, les corpuscules qui créent et subissent des interactions fortes, en plus des autres interactions, s’appellent hadrons ; tels sont les nucléons (proton, neutron), les hypérons, les résonances baryoniques, tous avec spin demi-entier, et aussi les mésons et les résonances mésoniques qui sont des hadrons avec spin entier.

Quarks

Tandis que l’on connaît actuellement six variétés de leptons, le nombre de hadrons est élevé ^{[cf. PARTICULES ÉLÉMENTAIRES]}. Pour comprendre cette grande diversité de hadrons, on a formulé le modèle des quarks , particules avec spin 1/2, charge et nombre baryonique fractionnaires, et qu’on postule comme constituants des hadrons. Ce modèle a été formulé en 1961 par Gell-Mann et Ne’eman ; ils ont postulé l’existence de trois quarks, dénotés u , d , s comme les composantes d’un élément d’un espace vectoriel complexe à trois dimensions sur lequel agit un certain groupe de transformations, le groupe SU(3). En 1982, on admet l’existence de six quarks, u , d , c , s , t , b , et l’étude des hadrons et la découverte de nouvelles particules ont apporté des évidences expérimentales (indirectes) pour l’existence des quarks, sauf pour le quark t . Chacun des six quarks (six arômes) existe en trois états, distingués par un nombre quantique appelé couleur .

Cette nouvelle «charge», la couleur des quarks, crée un champ, le champ de gluons, qui est, on l’admet, le responsable des interactions fortes entre les quarks. Ceux-ci sont censés être confinés à l’intérieur des hadrons qu’ils constituent: les baryons (hadrons à spin demi-entier) sont constitués de trois quarks, les mésons sont formés d’un quark et d’un antiquark. Ces quarks sont de couleurs telles que la charge couleur totale de la particule observable est nulle. Comme on n’a pas réussi à observer des quarks libres, on admet que les attractions entre quarks augmentent fortement avec la distance, de telle façon qu’elles empêchent leur libération.

Nous arrivons ainsi à la notion d’atome exotique, une notion qui généralise le concept usuel d’atome, en raison de l’existence de nouvelles particules élémentaires.

Atomes exotiques

Un atome, dans le sens habituel du terme, est un système constitué par un noyau et un nuage d’électrons, liés par les interactions électromagnétiques.

Si l’on remplace un ou plusieurs électrons, ou le noyau, ou les deux systèmes, par d’autres particules liées entre elles par un des types d’interaction, on aura un atome exotique .

Le premier – et le plus simple – exemple d’un atome exotique est le positronium , constitué d’un électron lié à un positron. Il s’agit d’un système important pour vérifier les prédictions de l’électrodynamique quantique. Lorsqu’un positron est créé et traverse la matière, il perd de l’énergie par l’émission successive de photons et finit par être capturé par un électron. Avant que l’annihilation ait lieu (chute de l’électron dans le «trou») avec production d’un certain nombre n de photons, le positron et l’électron forment un petit atome dont l’état fondamental, avec le nombre l = 0, est, soit un état ³S¹ (triplet; orthopositronium), le spin total du positronium étant s = 1, soit un état ¹S⁰ (singulet; parapositronium), avec un spin total nul; s (s + 1) 領 ² est la valeur propre de ひ²; le carré de l’opérateur du spin. Si l’on applique au vecteur d’état du positronium l’opération de conjugaison de charge (transformation des particules d’un état en antiparticules et vice versa), on trouve qu’un état quelconque du positronium, avec des nombres quantiques l et s définis, est un état propre de cet opérateur avec les valeurs propres (face=F0019 漣 1)^l+s (la parité de conjugaison de charge du positronium). Comme la parité de conjugaison de charge de n photons (état final) est (face=F0019 漣 1)ⁿ , et comme cette parité se conserve, on arrive aux règles de sélection suivantes:

– dans l’état ³S¹(l = 0, S = 1), le positronium ne peut pas s’annihiler avec production d’un nombre pair de photons (il disparaît avec l’émission de trois photons);

– dans l’état ¹S⁰ (l = 0, S = 0), le positronium ne peut pas disparaître en émettant un nombre impair de photons; la réaction ¹S⁰ 轢3 塚 est interdite.

On a pu mesurer la structure fine de l’état fondamental du positronium (différence d’énergie entre ³S¹ et ¹S⁰) et la vie moyenne de l’orthopositronium (face=F0019 力 1,4 憐 10 size=1^漣7 s) ainsi que celle du parapositronium (face=F0019 力 1,25 憐 10 size=1^漣10 s).

Un autre atome exotique qui, encore, ne met en jeu que des leptons, est le muonium : un électron lié à un muon positif. Tandis que dans le positronium on a affaire à un système particule-antiparticule (et donc toutes les deux avec la même masse), le muonium est une espèce d’isotope de l’atome d’hydrogène, la masse du muon positif étant environ un neuvième de celle du proton. L’intérêt de ce système est l’étude des propriétés électrodynamiques du muon, en particulier son moment magnétique, aussi bien que les effets possibles des interactions faibles sur les niveaux énergétiques du muonium.

L’atome d’hélium muonique est un autre atome exotique découvert en 1975 qui est constitué d’un noyau atomique d’hélium (particule alpha) entouré d’un muon négatif et d’un électron. Comme le rayon d’une orbite atomique de Bohr est inversement proportionnel à la masse du corpuscule, l’électron a une orbite autour du noyau ⁴He environ deux cents fois plus large que celle du muon, et l’image de l’hélium muonique, si l’on utilise le modèle de Bohr, est représentée à la figure 7.

Comme le cœur de cet atome, formé du noyau ⁴He et du muon négatif 猪^-, a une charge résultante positive, et comme son moment magnétique est celui de 猪^-, cet atome est un système d’étude complémentaire au muonium.

Il est clair que la notion d’atome exotique, généralisée, comme nous l’avons admise, comprend tous les systèmes de particules liées. Un deutéron est un atome exotique formé d’un proton lié à un neutron par l’intermédiaire des forces nucléaires.

De grand intérêt est la recherche des systèmes, tels que celui formé d’un proton et antiproton, p 樂 , qui peut donner des informations sur les interactions fortes entre ces particules. Ces recherches sont réalisées au moyen de collisions de faisceaux d’antiprotons, produits dans des accélérateurs à hautes énergies, contre des cibles d’hydrogène. La variation de la section efficace de ces collisions avec l’énergie des 樂 permet de caractériser l’existence d’états liés virtuels p 樂 , à certaines énergies, qui sont des résonances. On a ainsi récemment proclamé l’existence des résonances p 樂 avec pour masses: 1 936 MeV, 2 185 MeV, 2 355 MeV. Un certain nombre de résonances découvertes expérimentalement avec nombre baryonique nul sont connues sous le nom « baryonium »; elles se désintègrent notamment en paire-baryon-antibaryon plutôt qu’en mésons; les derniers états devraient être en fait prépondérants pour des raisons de cinématique.

Mentionnons encore que le proton, constitué d’un quark 猪 de couleur c ¹, d’un autre quark 猪 avec couleur c ² et d’un quark d avec couleur c ³, les couleurs étant combinées pour former une structure (antisymétrique) sans couleur, est, à son tour, un atome exotique, comme l’est aussi un méson, constitué d’un quark et d’antiquark (fig. 8).

L’étude des particules nouvelles, telles que le charmonium (c 縷 ) dans ses états J/ 祥, 祥 , etc., les systèmes upsilon (b 累 ), est importante pour la recherche de la nature et du comportement des forces d’interaction entre les quarks. Toute une nouvelle spectroscopie des atomes exotiques se développe et une théorie de jauge fondée sur le nombre quantique couleur – la chromodynamique ^{[cf. PARTICULES ÉLÉMENTAIRES]} – est en plein développement. L’espoir est que cette théorie soit en mesure de donner une description détaillée des forces entre les quarks à l’intérieur des hadrons aussi bien que les forces entre hadrons – les forces nucléaires de Yukawa (cf. FORCES NUCLÉAIRES).

4. Particules élémentaires et atomisme

Nous sommes donc aujourd’hui bien éloignés des notions de substance primordiale et d’atome indivisible héritées des philosophes grecs (tabl. 4). Avant la découverte de la structure électronique des atomes, les particules fondamentales dont seraient faites toutes les choses étaient les atomes des éléments figurant dans la classification périodique. La découverte de l’électron et du proton puis celle du neutron ont suscité l’espoir qu’on pût définir la totalité de la matière, comme divers agencements de ces trois particules (si ces particules remplaçaient la terre, l’eau et l’air, le photon, quantum de radiation électromagnétique, serait le grain de feu d’Empédocle). La découverte de nombreuses particules élémentaires, la plupart d’entre elles instables, a ruiné la conception du petit nombre de constituants fondamentaux de la matière. À l’heure actuelle, on réduit les forces dans l’univers à quatre interactions fondamentales et l’on cherche une théorie, fondée sur un groupe de symétrie suffisamment large pour unifier la description de ces interactions. Et si l’on attribue aux leptons et aux quarks le rôle de composants ultimes des particules, l’expérience suggère l’existence de six leptons et probablement de dix-huit quarks, sans parler du photon, du graviton, des trois bosons vectoriels et des gluons que l’on considère comme responsables pour les interactions fondamentales, en plus des bosons de Higgs, générateurs des masses des particules.

Si on spécule déjà sur une structure possible des leptons et des quarks, on peut se demander si l’atomisme n’a pas déjà rempli sa fonction en conduisant la science à son état actuel et si, désormais, pour décrire la matière on ne devrait pas plutôt renoncer à la recherche de sous-unités. La naissance de la mécanique quantique sous la forme de mécanique des matrices, on le sait, a été le résultat de la mise en question du concept de trajectoire de l’électron à l’intérieur de l’atome. Par quel schéma théorique devons-nous remplacer la question: quels sont les sous-composants des leptons et des quarks? En 1982, pour décider de certaines questions de la physique des particules telles que l’existence de quarks libres ou la diversité des neutrinos et leur possible masse, on fait appel à certains résultats d’astrophysique et de cosmologie. On peut donc espérer que la cosmologie présente des limitations à l’existence de sous-unités de la matière qui affecteraient les premiers instants de l’Univers et son évolution. Sans une telle théorie alternative, et aussi longtemps que les énergies disponibles permettent la fragmentation des corpuscules, on sera bien amené à pousser l’atomisme plus loin, à la recherche de l’unité insaisissable de la matière.

• athome v. 1350; lat. atomus, gr. atomos « indivisible »; cf. -tomie

1 ♦ Philos. Selon les atomistes anciens (Leucippe, Démocrite, Épicure, Lucrèce), Élément constitutif de la matière, indivisible et homogène. Atomes crochus.

♢ Fig. Chose d'une extrême petitesse. « Nous avons beau enfler nos conceptions, nous n'enfantons que des atomes, au prix de la réalité des choses » (Pascal). Il n'a pas un atome de bon sens. ⇒ brin, grain, parcelle.

2 ♦ (déb. XIX^e) Chim. Particule d'un élément chimique qui forme la plus petite quantité susceptible de se combiner. La molécule d'eau (H₂O) contient deux atomes d'hydrogène et un d'oxygène. — (v. 1900) Phys. nucl. Cette particule en tant que système complexe (selon des modèles conceptuels successifs). L'atome est formé d'un noyau (⇒ proton; neutron) et d'un nuage d'électrons. Atomes d'un corps simple différant par leur nombre de neutrons (⇒ isotope) . Atome radioactif; marqué. Fission du noyau de l'atome (⇒ atomique, nucléaire) .

Synonymes :

n. m.

d1./d CHIM Plus petite quantité d'un corps simple (de 0,1 à 1 millionième de millimètre) qui puisse entrer dans une combinaison.

|| PHYS Assemblage de particules négatives, appelées électrons, et de particules positives, appelées protons, et liées éventuellement à des neutrons au sein du noyau.

|| Par ext. L'atome: l'énergie atomique; ses applications.

d2./d Fig. Quantité minuscule. Il n'a pas un atome de bon sens.

d3./d PHILO Atomes crochus: dans le système de Démocrite et d'épicure, atomes qui peuvent s'accrocher les uns aux autres de façon à former les corps, la matière.

|| Fig. Atomes crochus entre deux personnes, affinités qui les rapprochent.

Encycl. Historique. - L'atome, "essence de toutes choses", ne fut dans l'Antiquité qu'un concept philosophique sans base scientifique. La première théorie atomique a été élaborée par Lavoisier, Proust, Dalton et Gay-Lussac entre 1789 et 1815. Elle se perfectionna grâce à Mendeleïev (classification périodique des éléments en 1868), Einstein (équivalence masse-énergie en 1900), Planck (théorie des quanta en 1905), Rutherford (découverte du noyau en 1911), Bohr et Sommerfeld (modèles de l'atome en 1913 et 1915), de Broglie (bases de la mécanique ondulatoire en 1923), Chadwick (découverte du neutron en 1932), I. et F. Joliot-Curie (transmutation artificielle en 1934), et aboutit à la mise au point du premier réacteur nucléaire en 1942 (V. divergence) et à l'explosion de la première bombe atomique en 1945. Structure de l'atome. - Bohr a élaboré un premier modèle (atome de Bohr), illustrant la structure de l'atome: autour d'un noyau central, chargé positivement, des électrons, chargés négativement, sont en mouvement. Pour expliquer le comportement des éléments autres que l'hydrogène, on supposa d'abord que les orbites décrites par l'électron pouvaient être elliptiques (atome de Sommerfeld) puis que l'électron tournait sur lui-même (hypothèse du spin, 1925). Un électron peut tourner dans un sens ou dans l'autre (spin égal à + 1/2 ou - 1/2). Le modèle actuel de l'atome repose sur la mécanique ondulatoire, dont les lois ont été définies par Louis Victor de Broglie. Un atome est défini par son nombre de masse A, qui indique le nombre de nucléons, et par son nombre de charge Z, qui indique le nombre de nucléons chargés positivement, ou protons (les autres nucléons, dont le nombre est A - Z, sont des neutrons).

⇒ATOME, subst. masc.

A.— Vx. Particule infiniment petite, insécable et homogène, constituant, avec d'autres éléments de même nature, la matière :

• 1. Leucippe et Démocrite admettent une substance primitive, décomposée en une infinité d'atomes en mouvement dans le vide...

E. PERRIER, La Philos. zool. avant Darwin, 1884, p. 4.

• 2. Cette fille lui plaisait et son épicurisme louait l'ordre des atomes qui la composaient.

A. FRANCE, Les Dieux ont soif, 1912, p. 178.

— P. hyperb. :

• 3. Pas un atome de poussière, pas une moisissure aux murs.

A. DAUDET, Le Nabab, 1877, p. 208.

— P. métaph. ou au fig. :

• 4. Le seul secret qui lui appartienne, et qu'il [Rubens] n'ait jamais livré, même aux plus sagaces, même aux mieux informés, (...) c'est ce point impondérable, insaisissable, cet atome irréductible, ce rien qui dans toutes les choses de ce monde, s'appelle l'inspiration, la grâce ou le don et qui est tout.

E. FROMENTIN, Les Maîtres d'autrefois, 1876, p. 55.

• 5. ... et je vous avouerai que je ne trouve pas dans tous les ouvrages des théologiens un atome de bon sens.

A. FRANCE, Les Dieux ont soif, 1912, p. 186.

• 6. Je comprenais ainsi que les paroles d'Albertine, quand on l'interrogeait, ne contenaient jamais un atome de vérité...

PROUST, La Prisonnière, 1922, p. 350.

Rem. Dans l'ex. suiv., atome, en appos., prend une valeur adj. :

• 7. ... et ce peuple privilégié, dont la perfection consiste à se couper un petit morceau de chair; ce peuple atôme, qui, dans l'océan des peuples, n'est qu'une petite vague, et qui veut que Dieu n'ait rien fait que pour lui seul, réduira encore de moitié, par son schisme, le poids déjà si léger qu'il établit dans la balance de l'univers.

VOLNEY, Les Ruines, 1791, p. 152.

— Loc. et au fig. Atomes crochus. [P. allus. à la philos. de Démocrite selon lequel les atomes constituent les corps en s'accrochant les uns aux autres] Sympathie, affinité qui s'établit entre deux êtres :

• 8. ... je ne sais que lui dire. Entre elle et moi il n'y a pas de ces atomes crochus qui font les relations suivies. Je crains que mes atomes à moi perdent tout leur pouvoir accrochant.

MÉRIMÉE, Lettres à M^me de la Rochejacquelein, 1870, p. 183.

1. CHIM. La plus petite partie d'un corps simple qui puisse entrer en combinaison avec une autre :

• 9. Les parties constitutives des molécules qui ne peuvent être divisées ni mécaniquement, ni chimiquement se nomment des atomes.

H. FONTAINE, Électrolyse, 1885, p. 13.

• 10. ... elles [les chlorophylles] ont même nombre d'atomes de carbone, un peu d'oxygène, mais leur molécule renferme de l'azote (...) et même un atome métallique, le magnésium.

L. PLANTEFOL, Cours de bot. et de biol. végétale, t. 1, 1931, p. 306.

— P. anal. PSYCHOL. Atomes psychiques. ,,Éléments qualitatifs indivisibles, de nature mentale, par le groupement desquels seraient formés, d'après certaines écoles, les états psychiques complexes`` (LAL. 1968). Cf. atomisme. SOCIOL. ,,Dans la terminologie de Moreno, l'atome social représente le pattern d'attractions et de répulsions réciproques exercées entre un individu et un groupe`` (PIÉRON 1963).

2. CHIM. et PHYS. NUCL. Partie d'un élément matériel conçue comme un système composé d'un noyau de protons et de neutrons autour desquels gravitent des électrons :

• 11. À la veille de la première guerre mondiale, une nouvelle notion importante, celle d'isotope, vint compléter la précédente : si pour un élément donné, le nombre total de protons présents dans les noyaux de ses atomes est constant et caractéristique, il n'en est souvent pas de même pour le nombre de neutrons qui peut varier de quelques unités. Les atomes d'un élément qui ne diffèrent que par le nombre de neutrons contenus dans leur noyau sont nommés des isotopes : ce sont de véritables jumeaux en raison de la quasi-identité de leurs propriétés physico-chimiques qui rend leur séparation extrêmement difficile, mais leurs caractères nucléaires sont très différents, et ce fait jouera un rôle de premier plan dans l'affaire atomique.

GOLDSCHMIDT, L'Aventure atomique, 1962, p. 15.

♦ Époque, ère, civilisation de l'atome. Ère caractérisée par l'exploitation militaire ou pacifique de l'énergie nucléaire.

— P. ext. ,,Le mot atome a été appliqué, depuis une dizaine d'années, à certains éléments physiques considérés comme finis, discontinus, indivisibles et répétés à un grand nombre d'exemplaires semblables : on a ainsi appelé atomes d'électricité les électrons; atomes d'énergie ou atomes d'action (...) les quanta de Planck, etc. (...) Le mot atome, en ce sens, n'est jamais employé seul, et ne doit pas l'être, si l'on veut éviter les équivoques`` (LAL. 1968).

PRONONC. ET ORTH. — 1. Forme phon. :[ato:m]. Le phonème o est fermé et long ,,dans la plupart des mots où il est suivi d'un seul m (...), qu'on l'écrive ou non avec un accent circonflexe`` (GRAMMONT Prononc. 1958, p. 18). BUBEN 1935, p. 41, indique que ces mots ,,prennent souvent un o bref, sous l'influence des mots en -omme``. FOUCHÉ Prononc. 1959, p. 79, indique que le [o] s'ouvre lorsqu'il devient inaccentué dans les dérivés : atomique, atomisme, etc. Enq. :/atom, D/. 2. Forme graph. — FÉR. Crit. t. 1 1787 écrit atôme.

ÉTYMOL. ET HIST. — 1. 1350-1400 philos. et phys. anc. athome « selon les philosophes anciens, le plus petit élément de matière, considéré comme indivisible » (Aalma, I, 709 ds Mélanges Haust, p. 352 : Athomus, athomes, c'est nom indevisible pour sa petitesse); 2. 1845 chim. atome « particule d'un élément chimique qui forme la plus petite quantité susceptible de se combiner » (BESCH.); 3. 1930 phys. nucléaire « cette particule en tant que formant elle-même un système complexe » (R. RUYER, Esquisse d'une philos. de la structure, p. 311 : ... grâce au progrès des hypothèses sur la structure de l'atome ... [p. 332] ... C'est encore une chance que chaque atome soit capable d'émettre des radiations lumineuses).

Empr. au lat. atomus, attesté au sens 1 dep. Lucilius (TLL s.v., 1046, 20; cf. CICÉRON, Fin., 1, 17, ibid., 1046, 23 : Democritus atomos quas appellat, id est corpora individua propter soliditatem, censet in infinito inani... ita ferri, ut concursionibus inter se cohaerescant... eumque motum atomorum nullo a principio, sed ex aeterno tempore intelligi convenire), lui-même empr. au gr. , de même sens, littéralement « qu'on ne peut couper, indivisible ».

STAT. — Fréq. abs. littér. :968. Fréq. rel. littér. : XIX^e s. : a) 991, b) 1 738; XX^e s. : a) 1 137, b) 1 654.

BBG. — ARNAUD 1966. — BOUILLET 1859. — CHAMB. 1970. — CHARLES 1960. — CHESN. 1857. — DUCH. 1967, § 7, 62. — DUVAL 1959. — Électron. 1963-64. — FOULQ.-ST-JEAN 1962. — FROMH.-KING 1968. — GALIANA Déc. sc. 1968. — GOBLOT 1920. — GRAND. 1962. — JULIA 1964. — LAITIER 1969. — LAL. 1968. — LARCH. 1880. — LITTRÉ-ROBIN 1865. — Méd. Biol. t. 1 1970. — MIQ. 1967. — MUCCH. Sc. soc. 1969. — MUSSET-LLORET 1964. — NEYRON 1970. — Nucl. 1964. — NYSTEN 1814. — OSTOYA s. d. — PIÉRON 1963. — PLAIS.-CAILL. 1958. — PRIVAT-FOC. 1870. — ROS.-IOUD. 1955. — SILL. 1965. — Sociol. 1970. — UV.-CHAPMAN 1956.

atome [atom] n. m.

ÉTYM. 1350-1400, athome; lat. atomus, du grec atomos « qu'on ne peut couper, indivisible », de a- privatif, et tomein « couper, diviser » → Tome, -tomie.

❖

———

I Vx ou emplois fig. Particule matérielle, considérée comme indivisible.

1 a Vx ou hist. des sc., de la philos. Selon les atomistes anciens (Leucippe, Démocrite, Épicure, Lucrèce), Élément constitutif de la matière, indivisible et homogène. || Démocrite et Épicure ont prétendu que le monde était composé d'atomes, que les corps se formaient par la rencontre fortuite des atomes (Académie).