Akademik

ANALYSE MATHÉMATIQUE

ANALYSE MATHÉMATIQUE

L’analyse mathématique est le développement des notions et résultats fondamentaux du calcul infinitésimal. Ce dernier s’était déjà considérablement enrichi et diversifié entre les mains des mathématiciens du XVIII^e siècle, avant tout Euler et Lagrange. À partir de 1800, cette diversification s’accentue encore et s’accompagne d’un nouvel état d’esprit. Nous allons essayer, dans cet article, de donner une vue d’ensemble de cette évolution au cours du XIX^e siècle et au début du XX^e siècle, en renvoyant pour les détails aux articles spécialisés.

Il est difficile de décrire en une phrase l’«analyse moderne», aboutissement de cette évolution; en la prenant dans son acception la plus large, on peut dire que l’on fait de l’analyse lorsqu’on calcule sur les notions de limite ou de continuité ; il y a donc fort peu de parties des mathématiques où l’analyse n’intervienne sous une forme ou une autre.

Mais ce qui distingue l’analyse mathématique actuelle, c’est, d’une part, qu’au lieu de limiter les domaines décrits par les «variables» et les valeurs des fonctions à des ouverts dans les espaces Rⁿ elle peut envisager le cas où ces domaines sont des variétés différentielles quelconques (cf. infra ); et, d’autre part, qu’elle s’appuie dans une large mesure sur les résultats généraux d’algèbre et de topologie qui forment l’armature de la théorie des espaces fonctionnels (cf. infra ).

1. La théorie des fonctions analytiques

La notion de fonction remonte au XVII^e siècle; mais jusque vers 1800, on admettait généralement qu’une fonction f d’une variable réelle, définie dans un intervalle, était indéfiniment dérivable, sauf en un nombre fini de points exceptionnels. On peut, pour une telle fonction, et pour tout point non exceptionnel x ⁰, former la série de Taylor de f au point x ⁰:

et comme les idées sur la convergence des séries étaient restées des plus floues, on admettait que la fonction «était» sa série de Taylor au voisinage du point x ⁰. L’usage de plus en plus répandu des nombres complexes permettait en outre de parler de telles séries pour des valeurs complexes des variables x et x ⁰et des coefficients (bien qu’en l’absence d’une représentation géométrique des nombres complexes l’utilisation de telles «fonctions d’une variable complexe» demeurât assez limitée).

Le début du XIX^e siècle est caractérisé tout d’abord par un retour à la rigueur, notamment dans l’emploi des séries, où, sous l’influence de Gauss et surtout d’Abel et de Cauchy, il est assez rapidement admis qu’une série n’a de sens que lorsqu’on a prouvé sa convergence. Or, une fonction d’une variable réelle peut être indéfiniment dérivable dans un intervalle |x 漣 x ⁰| 諒見, sans que sa série de Taylor au point x ⁰ converge pour x x ⁰; il se peut aussi que la série de Taylor au point x ⁰soit convergente pour tout x , mais que sa somme soit différente de la fonction d’où l’on est parti (ce dernier cas se présente par exemple pour la fonction égale à exp (face=F0019 漣 1/x ²) pour x 0 et à 0 pour x = 0, en prenant x ⁰ = 0). Il y a donc lieu de faire l’étude des fonctions, dites analytiques , qui, au voisinage de chaque point x ⁰où elles sont définies, sont égales à leur série de Taylor en ce point. On savait depuis longtemps que les fonctions rationnelles, ou la fonction e ^x , étaient analytiques; Abel prouva qu’il en est de même de x 猪 et de log x (pour x 礪 0). Mais c’est Cauchy qui est l’initiateur de la théorie générale des fonctions analytiques.

Il a l’heureuse idée de se placer d’emblée dans le domaine complexe (où l’on dit aussi alors «fonction holomorphe » au lieu de « fonction analytique »), et en quelques années progresse à pas de géant grâce à l’introduction d’un outil très puissant, les intégrales curvilignes dans le plan complexe. Si D est un ouvert du plan complexe C, 塚:[ 見, 廓]D un «arc de courbe» dans D (c’est-à-dire une fonction complexe continûment dérivable, définie dans un intervalle compact [ 見, 廓] de R et à valeurs dans D), f une fonction complexe continue (mais non nécessairement analytique) dans D, on note:

l’intégrale:

obtenue par le «changement de variable» z = 塚(t ). Le résultat essentiel obtenu par Cauchy exprime une remarquable «solidarité» entre les valeurs d’une fonction holomorphe f dans D: soit : |z 漣 z ⁰| 諒 r un disque fermé contenu dans D, et 塚: t 料 z ⁰ + re ^it le «circuit» formé par sa «circonférence parcourue une fois dans le sens positif» (0 諒 t 諒 2 神); alors, pour tout point 﨣 intérieur à (donc tel que |z 漣﨣| 麗 r ) on a la formule de Cauchy :

qui montre entre autres que les valeurs de f sur la circonférence déterminent sans ambiguïté ses valeurs dans tout le disque.

La théorie des fonctions analytiques d’une variable complexe n’a plus cessé depuis Cauchy d’être un sujet de prédilection de très nombreux mathématiciens, et une masse imposante de résultats intéressants a été obtenue. Au XX^e siècle, cette théorie a été généralisée aux fonctions de plusieurs variables complexes, dont les propriétés sont très différentes de celles des fonctions d’une variable complexe; cette dernière théorie est elle-même devenue une partie de la théorie plus vaste des espaces analytiques, où s’insère aussi la théorie plus ancienne des surfaces de Riemann.

Il faut enfin souligner les remarquables applications (séries de Dirichlet, méthode de Hardy-Littlewood) de la théorie de Cauchy à des problèmes difficiles de théorie des nombres (cf. théorie des NOMBRES – Théorie analytique).

2. Fonctions elliptiques

Un des plus beaux exemples de l’élargissement apporté à l’analyse classique par la considération des fonctions de variables complexes est fourni par la théorie des fonctions elliptiques, développée par Abel et Jacobi indépendamment des premiers travaux de Cauchy (une bonne part de leurs résultats et même des développements plus tardifs sur la fonction modulaire ont d’ailleurs été retrouvés dans les papiers non publiés de Gauss, datant des environs de 1800).

Depuis le milieu du XVII^e siècle, le calcul de la longueur d’un arc d’ellipse posait aux analystes un problème non résolu: il s’agissait d’exprimer «en termes finis» (c’est-à-dire par une combinaison de «fonctions élémentaires» telles que x size=1^見, log x , e^x ) l’intégrale elliptique:

(k réel 0, 梁 1).

Liouville devait prouver plus tard qu’il n’existe pas de telle expression, mais dès la fin du XVIII^e siècle, on commençait à étudier les propriétés de la fonction I(x ) comme une nouvelle «transcendante».

Le progrès considérable dû à Abel et à Jacobi consista d’une part à considérer la fonction «inverse» x =snu définie par I(x )=u , par une extension hardie du procédé qui peut servir à définir la fonction sin u comme solution de:

et d’autre part à donner à u des valeurs complexes. Cette extension du domaine de la «fonction elliptique» sn u mit aussitôt en évidence sa propriété fondamentale de double périodicité: il y a deux nombres réels non nuls K, K tels que:

Les nouvelles fonctions ainsi introduites devaient jouer un rôle très important en analyse, en géométrie algébrique et en théorie des nombres.

Déjà, avec Abel et Jacobi, avait commencé l’étude des «intégrales abéliennes »:

généralisation très vaste des intégrales elliptiques, où y est une «fonction algébrique» de x , définie par une équation polynomiale P(x , y ) = 0, et R(x , y ) une fraction rationnelle en x et y ; pour le cas où y ² = Q (x ), où Q est un polynôme du 5^e degré, Jacobi avait résolu le problème d’«inversion» analogue à celui de l’intégrale elliptique: il avait montré que, pour obtenir des fonctions analytiques «uniformes», il faut considérer, non pas l’unique équation:

mais deux équations:

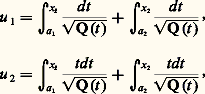
et que, de ces équations, on tire les fonctions symétriques x ¹ + x ² et x ¹x ² comme fonctions analytiques des deux variables complexes u ¹, u ², ces fonctions étant quadruplement périodiques. Weierstrass et Riemann menèrent à bien la solution du problème général, qui introduit un invariant algébrique fondamental, l’entier p dit « genre » de la courbe algébrique P(x , y ) = 0; la solution fait alors intervenir des fonctions analytiques de p variables complexes, les «fonctions abéliennes», qui sont 2p fois périodiques. Indiquons que la théorie contemporaine des fonctions automorphes constitue une vaste généralisation des fonctions elliptiques et abéliennes, où le «groupe des périodes» Z^2p est remplacé par un sous-groupe discret du groupe unimodulaire SL (n , C).

3. Équations différentielles et équations aux dérivées partielles

Les équations différentielles s’étaient présentées dès le début du calcul infinitésimal, soit à propos de la détermination de courbes vérifiant certaines propriétés différentielles, soit comme traductions mathématiques de problèmes de mécanique, d’astronomie ou de physique. Au cours du XVIII^e siècle, les développements des applications des mathématiques à la physique avaient introduit des équations aux dérivées partielles, qui apparaissent aussi par ailleurs dans les problèmes de la naissante théorie des surfaces.

Dans l’étude de ces équations, le XIX^e siècle se marque encore par un changement de point de vue assez net: au XVIII^e siècle, on se souciait surtout de trouver des méthodes d’étude pour des équations de type assez spécial, mais donnant les solutions sous forme explicite , par des «quadratures» portant sur des combinaisons algébriques des fonctions données (autrement dit, on cherchait à ramener les équations proposées à des résolutions d’équations du type particulier y = f (x ), comme on avait cherché à résoudre les équations algébriques en les ramenant aux équations binômes x ⁿ = a ).

Au contraire, à partir de Cauchy, on s’attaque aux équations les plus générales, et on précise les «conditions initiales» additionnelles auxquelles on assujettit les solutions, de façon à obtenir, sous des conditions très larges, des théorèmes d’existence et d’unicité, ainsi que des procédés d’approximation de la solution. Mentionnons seulement ici les deux plus simples de ces théorèmes: pour une équation différentielle de la forme y = f (x , y ) avec second membre continûment différentiable, il existe, au voisinage d’un point x ⁰, une et une seule solution y = u (x ) de l’équation telle que u (x ⁰) soit un nombre donné y ⁰. De même, pour une équation aux dérivées partielles de la forme:

avec second membre continûment différentiable, il existe, au voisinage d’un point (x ⁰, y ⁰), une et une seule solution z = u (x , y ) de l’équation telle que u (x ⁰, y ) soit une fonction donnée 﨏 (y ).

De Cauchy à nos jours, les problèmes soulevés par la théorie des équations différentielles et des équations aux dérivées partielles n’ont cessé d’être un des plus vigoureux stimulants du développement de l’analyse, suscitant la naissance et le développement de nouvelles théories, qui souvent se sont révélées d’une importance bien plus grande que le problème particulier qui leur avait donné naissance. Les plus importants de ces développements sont les suivants:

A) Pour les équations aux dérivées partielles (et les systèmes de telles équations), les théorèmes de Cauchy ne s’appliquent qu’à des types assez restreints d’équations. Leur extension à des cas plus généraux et l’examen des cas où ils perdent leur validité (données initiales «caractéristiques») ont fait l’objet de la théorie des systèmes différentiels dont l’expression la plus générale et la plus élégante a été donnée par É. Cartan, et où il reste encore beaucoup de points à élucider.

B) Les théorèmes d’existence et d’unicité de Cauchy sont de nature locale tant en ce qui concerne les conditions initiales que l’existence de la solution. D’autres types de «conditions aux limites» pour les équations différentielles et les équations aux dérivées partielles, de nature globale (c’est-à-dire impliquant les valeurs de la solution ou de ses dérivées dans tout son domaine d’existence, et non plus seulement au voisinage d’un point), se sont naturellement présentés dans les applications à la physique mathématique (problèmes de Sturm-Liouville, de Dirichlet, de Neumann, etc.), et leur solution a eu de nombreuses répercussions en mathématiques pures. C’est en particulier à propos de ces problèmes qu’a pris naissance l’analyse fonctionnelle moderne, dont nous parlerons un peu plus loin.

C) En ce qui concerne les équations aux dérivées partielles, Cauchy n’avait considéré que des équations, des conditions initiales et des solutions analytiques. L’extension de ses résultats à des fonctions plus générales (même seulement aux fonctions indéfiniment différentiables) conduit à des difficultés inattendues. Un problème voisin est celui de la manière dont «varie» une solution lorsqu’on fait «peu» varier les conditions initiales. Tous ces problèmes ont pu être formulés et attaqués avec succès grâce aux conceptions et aux ressources de l’analyse fonctionnelle.

D) Pour les systèmes d’équations différentielles ordinaires, lorsqu’on envisage les solutions dans tout leur domaine d’existence, le problème de «variation» de la solution avec les conditions initiales, dont nous venons de parler, a conduit aux importantes études sur les divers concepts de «stabilité», commençant avec les célèbres travaux de H. Poincaré et de Liapounoff, et qui continue à faire l’objet de nombreuses recherches aussi bien théoriques qu’appliquées à d’innombrables questions posées par la mécanique et la physique.

E) Toujours pour les systèmes d’équations différentielles, on a pu, dans certains cas assez généraux, obtenir des résultats très profonds sur l’ensemble de toutes les solutions d’un système donné, tant dans le domaine réel (Poincaré-Bendixson) que dans le domaine complexe (Painlevé).

F) Enfin, on a fait des études approfondies de solutions d’équations différentielles particulières (fonctions de Bessel, de Legendre, de Mathieu, etc.) qui ont acquis droit de cité comme nouvelles «transcendantes» à côté des «fonctions élémentaires» traditionnelles; certaines équations aux dérivées partielles particulières, provenant de nombreux problèmes de physique (équation de Laplace, équation des ondes, équation de la chaleur, équations de l’hydrodynamique, etc.) n’ont cessé, depuis près de deux siècles, de faire l’objet d’actives recherches, conduisant à de vastes théories comme celle du potentiel; les «fonctions spéciales» mentionnées ci-dessus sont notamment liées à l’équation de Laplace.

4. L’avènement de la théorie des ensembles et de la topologie

La notion de limite est la base même du calcul infinitésimal; mais, bien que certains d’entre eux, dont d’Alembert, aient approché d’une définition pour nous correcte, les mathématiciens du XVIII^e siècle étaient hors d’état de développer une théorie mathématique rigoureuse du «calcul», sur le modèle de la géométrie grecque, et devaient se contenter de justifications heuristiques de leurs découvertes.

C’est seulement avec Bolzano, Abel et Cauchy que les notions de limite et de continuité sont enfin définies sans ambiguïté et de façon utilisable dans les démonstrations. À cette occasion, Bolzano et Cauchy dégagent le critère fondamental (dit «critère de Cauchy») d’existence de la limite d’une suite (u ⁿ ) de nombres réels: pour tout 﨎礪 0, il existe un entier n ⁰ tel que, si m et n sont tous deux au moins égaux à n ⁰, on a | u ^m 漣 u ⁿ | 諒﨎 (autrement dit, à partir d’un certain rang, tous les termes de la suite sont «très voisins les uns des autres»); son grand intérêt est qu’il permet de prouver l’existence d’une limite sans connaître à l’avance sa valeur. Ce critère est d’ailleurs équivalent à l’existence de la borne supérieure d’un ensemble majoré de nombres réels, ou au «principe des intervalles emboîtés», suivant lequel une suite dénombrable d’intervalles fermés bornés dont chacun contient le suivant a nécessairement un point commun. Cauchy semble avoir considéré ce dernier principe comme évident; de fait, il peut, avec les propriétés usuelles des nombres réels vis-à-vis des opérations algébriques et de la relation d’ordre, servir de caractérisation axiomatique à ces nombres (cf. nombres RÉELS).

Mais, vers le milieu du XIX^e siècle, avec l’élargissement de la notion de fonction, commencent à apparaître, en analyse, les «monstres», êtres mathématiques aux propriétés insolites, en opposition flagrante avec l’«intuition» que nous croyons avoir de l’espace: «courbes» sans tangente en aucun point, «courbes» remplissant tout un carré, etc. Les constructions conduisant à ces objets extraordinaires étaient en tout point rigoureuses, une fois admis le critère de Cauchy; on pouvait à bon droit se demander si ce dernier ne recelait pas le germe de contradictions dont les «monstres» auraient été les manifestations. Ce doute fut levé par les travaux à peu près simultanés de Weierstrass, de Méray, de Cantor et de Dedekind, qui, par divers procédés, définirent les nombres réels à partir des nombres rationnels, au moyen de l’opération que nous appelons maintenant complétion, assurant donc la non-contradiction de l’analyse, pourvu que soit admise celle de l’arithmétique.

En même temps, les progrès de l’analyse amenaient Cantor à dégager deux types de notions toutes nouvelles: d’une part, les concepts de correspondance biunivoque, de dénombrabilité (et, plus généralement, de puissance d’un ensemble), et plus tard celui d’itération «transfinie», qui inauguraient la théorie générale des ensembles; d’autre part, dans l’ensemble R des nombres réels, puis dans le plan et les espaces à n dimensions Rⁿ , les idées de point d’accumulation, d’ensemble fermé, d’ensemble parfait, d’ensemble ouvert, qui allaient donner naissance à la topologie.

Mais pour fonder cette dernière, il fallait encore que fût dégagée de façon précise la notion capitale d’homéomorphisme. Les remarquables découvertes de Cantor sur les puissances des ensembles y contribuèrent pour une bonne part: quand il eut prouvé qu’un segment de droite non réduit à un point et un carré pouvait être mis en correspondance biunivoque, Dedekind comprit aussitôt que ce résultat surprenant, en contradiction absolue avec notre «intuition» de l’espace, ne devait plus subsister si l’on exigeait de la correspondance biunivoque qu’elle soit continue dans les deux sens , c’est-à-dire ce qu’on appelle maintenant une homéomorphie. D’autre part, Riemann (en développant, en vue d’applications aux fonctions abéliennes, la théorie des surfaces qui portent son nom) et ses contemporains (Listing, Jordan) s’étaient aperçus que certaines propriétés des «figures» de l’espace restaient inchangées par une «déformation» arbitraire (par exemple on ne peut «déformer continûment» un tore en une sphère) et avaient attiré l’attention sur l’importance de ces propriétés dans beaucoup de questions d’analyse. Dès lors était en principe fondée la nouvelle branche des mathématiques appelée d’abord analysis situs , et maintenant topologie , dont on peut dire que l’un des buts principaux est d’étudier, et si possible de caractériser par un système d’invariants (numériques ou de nature algébrique, comme des groupes ou anneaux attachés à l’espace), les classes d’«espaces» deux à deux homéomorphes, ou pouvant se déduire l’un de l’autre par «déformation continue» (notion qui, en fait, est un peu plus forte que celle d’homéomorphie).

Les «espaces» surtout considérés au début étaient homéomorphes à des polyèdres ou à leurs généralisations n- dimensionnelles: les «polytopes» et les «complexes», car c’était ce genre de «figures» qui intervenaient surtout dans les mathématiques classiques; c’est d’ailleurs ce type d’espaces qui joue le plus grand rôle dans les immenses développements qu’ont connus depuis le début du XX^e siècle la topologie algébrique et sa progéniture, la topologie différentielle, qui s’occupe des invariants liés à la fois à la topologie et à la structure différentielle des «variétés différentielles» (cf. infra ). Mais les idées fondamentales de la topologie (qui, ainsi qu’on s’en aperçut rapidement, forment la vraie base des notions de limite et de continuité) allaient rapidement déborder ce cadre, et, dès la fin du XIX^e siècle, se révéler un appui précieux pour le développement de l’analyse fonctionnelle (cf. infra ).

5. Mesure et intégration

La conception de l’intégrale au XVIII^e siècle reposait sur la notion intuitive d’«aire»: pour une fonction f (x ), continue et 閭 0 dans un intervalle a 諒 x 諒 b , l’intégrale:

était l’aire comprise entre la courbe y = f (x ), l’axe Ox et les deux droites x = a et x = b . Avec la remise en ordre générale de l’analyse entreprise par Cauchy, on revient à une définition rigoureuse n’empruntant rien à l’intuition de l’espace: la valeur de l’intégrale est par définition prise comme limite, pour n tendant vers + 秊, des sommes:

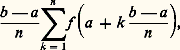
dites souvent «sommes de Riemann» (bien qu’en fait l’idée de considérer ces «valeurs approchées» de l’intégrale remonte à Eudoxe et Archimède et ait été l’inspiration des inventeurs du calcul intégral au XVII^e siècle). La contribution de Riemann lui-même fut de s’apercevoir que les sommes précédentes ont encore une limite lorsque la fonction f n’est plus nécessairement continue, mais a un ensemble de points de discontinuité qui, pour tout 﨎礪 0, peut être contenu dans une réunion finie d’intervalles dont la somme des longueurs est 諒﨎.

L’intérêt propre de ce résultat était assez mince, mais il déclencha, dans le dernier tiers du XIX^e siècle, toute une série d’études en vue de définir, dans des cas aussi généraux que possible, une notion de «mesure» des sous-ensembles de R, et d’«intégrale» d’une fonction de variable réelle. Elles devaient finalement aboutir, vers 1900, avec Émile Borel et Henri Lebesgue, à la définition de l’«intégrale de Lebesgue, que l’expérience a montré être la notion d’«intégrale» commode et féconde pour d’innombrables applications.

D’autre part, en vue d’étudier un problème particulier d’analyse, Stieltjes, en 1894, élargit la définition traditionnelle de «mesure» sur R, qui donne pour «mesure» des intervalles d’extrémités a et b le nombre b 漣 a ; Stieltjes considère plus généralement une fonction croissante 﨏, continue à droite (c’est-à-dire, telle que 﨏(x ⁺) = 﨏(x )), et prend comme définition de la «mesure» de l’intervalle a 麗 x 諒b le nombre 﨏(b ) 漣﨏(a ), calquant ensuite la définition de l’intégrale:

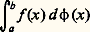
sur celle de Cauchy. Un des intérêts de cette généralisation est qu’elle donne un sens mathématique aux «mesures ponctuelles» des physiciens: aux points a où la fonction 﨏 est discontinue, l’ensemblea a une «mesure» non nulle égale au «saut» 﨏(a ) 漣﨏(a ^-) de 﨏 (ce qui implique naturellement que les quatre intervalles ayant pour extrémités a et b [qui peuvent ou non appartenir à l’intervalle] n’ont pas nécessairement même «mesure»). En outre, les méthodes de Lebesgue s’appliquent aussi à cette «mesure» plus générale, et on s’est aperçu plus récemment qu’elles sont valables dans des «espaces» beaucoup plus généraux que R, ce qui a donné à l’intégration un rôle de premier plan aussi bien dans l’analyse fonctionnelle que dans le calcul des probabilités.

6. Théorie spectrale et analyse fonctionnelle

On sait qu’un problème célèbre de mécanique consiste à déterminer les «petites oscillations» au voisinage d’une position d’équilibre d’un système formé d’un nombre fini de solides, donc «à un nombre fini de degrés de liberté» (ce qui signifie que l’état du système est entièrement connu par la donnée d’un nombre fini de paramètres réels q ^j (1 諒 j 諒 n ) qui varient en fonction du temps t ). La solution, due à Lagrange, consiste à chercher les «oscillations propres» (ou «en phase»), c’est-à-dire de la forme q ^j (t ) = c ^j 﨏(t ), où c ^j est une constante, et où figure pour tous les indices j la même fonction du temps 﨏 (t ); en admettant que l’énergie du système est un polynôme quadratique par rapport aux q ^j , et en cherchant, pour la commodité du calcul, les solutions complexes des équations du mouvement, on trouve qu’il n’y a qu’un nombre fini de fonctions 﨏(t ) possibles, de la forme exp (i^k t ), où les nombres^2k sont les valeurs propres d’une matrice carrée symétrique U = (a ^ji ) d’ordre n. Si les^2k sont supposés distincts, il correspond à chacun d’eux un vecteur propre c ^k = (c ^kj ) 1 諒 j 諒 n , solution de l’équation U 練x =^2k x (cf. algèbre LINÉAIRE ET MULTILINÉAIRE); toute «oscillation» du système donné est alors combinaison linéaire des oscillations propres q ^k (t ) = c ^k exp (i^k t ).

La mécanique des milieux continus conduisait à des problèmes analogues, mais avec «une infinité de degrés de liberté»; les exemples les plus simples en sont les petites oscillations d’une corde ou d’une membrane tendue: la forme de la corde (ou de la membrane) ne peut être décrite par un nombre fini de fonctions du temps seul, mais bien par une fonction u (x, t ), ou u (x, y, t ), qui représente le déplacement à l’instant t du point d’abscisse x (respectivement de coordonnées x, y ) sur la corde (ou la membrane). Les oscillations «en phase», où tous les points se meuvent «de la même façon» dans le temps, sont ici observables expérimentalement (ce sont les «sons harmoniques»). Mathématiquement, elles correspondent à des solutions de la forme u (x, t ) = v (x ) 﨏(t ) pour la corde (respectivement u (x , y , t )=v (x , y ) 﨏(t ) pour la membrane). On trouve encore que la fonction 﨏(t ) doit, dans les deux cas, être de la forme exp (it ) et l’on a alors pour la corde homogène l’équation v +²v = 0, pour la membrane l’équation:

Il faut exprimer en outre que la corde est fixée en ses extrémités, ce qui donne (en supposant que ces extrémités sont x = 0 et c = 1) v (0) = v (1) = 0, et que la membrane est fixée sur son contour 臨, ce qui donne v (x, y ) = 0 le long de la courbe 臨; c’est ce qu’on appelle les conditions aux limites du problème (fort différentes, comme on le voit, des «conditions initiales» de Cauchy). La solution est très simple pour la corde homogène, puisqu’on intègre explicitement l’équation v +²v = 0: on trouve aussitôt qu’on doit avoir² = n ² 神², où n est entier , ce qui concorde avec les résultats expérimentaux. Mais déjà lorsque la corde n’est pas homogène, l’équation donnant v (x ) (avec les mêmes conditions aux limites) est:

où p (x ) et 福(x ) sont des fonctions continues quelconques, et où on ne peut donc espérer avoir explicitement l’intégrale générale de l’équation; le problème paraît donc beaucoup moins aisé, et il est encore plus difficile pour l’équation des membranes (1) lorsque le contour 臨 est quelconque.

L’idée générale qui permit de vaincre ces difficultés est celle du «passage du fini à l’infini». Cette idée fut déjà exprimée au XVIII^e siècle par Daniel Bernoulli: l’illustre savant considérait l’oscillation d’une corde tendue comme «limite» de l’oscillation d’un système de n «masses ponctuelles» placées sur la corde, lorsque n tend vers + 秊. Bornons-nous, pour simplifier, au cas de l’équation (2). On prouve aisément l’existence d’une fonction continue de deux variables K(x, y ) (c’est la «fonction de Green» du problème) telle que K(y, x ) = K(x, y ) et que les solutions v (x ) de l’équation (2) vérifiant les conditions aux limites v (0) = v (1) = 0 soient exactement les solutions de l’équation intégrale :

(avec 猪 =²).

Une première méthode de «passage du fini à l’infini» (Fredholm) consiste à remplacer dans (3) l’intégrale par une «somme de Riemann»:

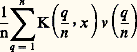
et à déterminer les valeurs x ^p = v (p/n ) par le système linéaire approché:

Chaque système (4) est du type:

et il paraît donc plausible que les n valeurs propres 猪^jn de la matrice (a ^pq ) tendent vers des limites 猪^j lorsque n tend vers + 秊, qui seraient les seules valeurs possibles de 猪 pour lesquelles l’équation (3) admettrait des solutions non identiquement nulles, ce qui rendrait compte des «sons harmoniques» observés expérimentalement.

On peut effectivement prouver cette convergence, mais il est beaucoup plus fructueux d’attaquer le problème par une méthode différente (Hilbert). On cherche à déterminer la solution v de (3) à l’aide de ses coefficients de Fourier:

où les 諸^p désignent les fonctions du système orthonormal trigonométrique (proportionnelles aux fonctions cos n 神x et sin n 神x ). Les x ^p satisfont à la relation de Parseval:

et si l’on pose

on obtient pour les x ^p un système d’une infinité d’équations linéaires:

dont l’analogie formelle avec (5) est évidente.

Le pas décisif qui conduit à l’analyse fonctionnelle moderne est de concevoir une théorie plus vaste qui englobe à la fois le cas classique (5) du problème des valeurs propres et les systèmes (8) soumis aux conditions (6). On observe pour cela que les suites x = (x ^p ) de nombres réels telles que:

forment un espace vectoriel (cf. algèbre LINÉAIRE ET MULTILINÉAIRE) de dimension infinie que l’on appelle l’espace de Hilbert H. On tire aisément de la définition (7) que l’on a:

et que pour tout «vecteur» x 捻 H, la série:

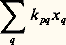
est convergente; en outre, si y ^p est sa somme, la suite y = (y ^p ) appartient encore à H; on peut donc écrire y = U 練x , où U est une application linéaire de l’espace vectoriel H dans lui-même. Une fois ces notations posées, le système d’équations (8) prend exactement la forme (5). Mais pour que cette généralisation ne soit pas purement formelle, il faut qu’on puisse avoir des critères maniables d’existence et d’unicité des solutions de ces équations plus générales; on constate qu’il faut pour cela restreindre la classe des applications linéaires U de H dans lui-même que l’on considère, en leur imposant des conditions supplémentaires qui s’expriment sous une forme particulièrement commode dans le langage de la topologie et sont vérifiées dans le cas particulier de (8).

C’est là l’extension des concepts topologiques à des «espaces de dimension infinie» à laquelle nous avons fait allusion plus haut: par une généralisation naturelle de la géométrie euclidienne, on convient d’appeler distance de deux «points» x, y de H le nombre:

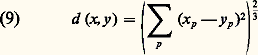
et on prouve alors sans peine que cette expression possède la plupart des propriétés de la distance euclidienne classique, notamment les suivantes:

I. d (x, y ) 閭 0, et d (x, y ) = 0 si et seulement si x = y ;

II. d (y, x ) = d (x, y );

III. d (x, z ) 諒 d (x, y ) + d (y, z ) («inégalité du triangle»).

Il suffit alors d’observer que les notions topologiques fondamentales dans Rⁿ : ensemble ouvert, ensemble fermé, limite, continuité, peuvent se définir en partant exclusivement de la notion de distance et en n’utilisant que les propriétés (I), (II), (III) ci-dessus; on peut donc transporter toutes ces notions à l’espace de Hilbert, et les conditions à imposer à U s’expriment alors à l’aide de la notion de «limite» ainsi définie.

Nous nous sommes étendus sur cet exemple à cause de sa simplicité et de son importance considérable dans les applications les plus variées. (Le nom même de «spectre» donné à l’ensemble des «valeurs propres» et à ses généralisations rappelle le rôle capital joué par ces notions dans toutes les questions de physique où interviennent des oscillations, et plus récemment – et d’une manière surprenante – en mécanique quantique.) Mais il invite aussitôt à des généralisations bien plus vastes: lorsque sur un ensemble quelconque E, on peut définir une fonction «distance» d (x,y ) pour deux éléments quelconques x, y , soumise uniquement aux conditions (I), (II) et (III) ci-dessus, on peut procéder comme pour H et définir donc dans E des notions topologiques. En fait, même avant les travaux de Hilbert, on avait remarqué que dans de nombreux «espaces fonctionnels» (c’est-à-dire des ensembles dont les éléments sont des fonctions ), on peut, et par de multiples procédés, définir de telles «distances». Un des exemples les plus anciens est celui de l’ensemble face=F9796 C(I) des fonctions continues dans un intervalle I = [a,b ]; on peut y prendre comme «distance», soit le nombre:

soit le nombre:

exemple particulièrement intéressant, car les notions topologiques déduites de ces deux distances sont différentes , fournissant un exemple très naturel de plusieurs «topologies» distinctes sur un même ensemble. D’autres exemples analogues proviennent du développement du calcul des variations.

Ce n’est là que le début de l’invasion spectaculaire de l’analyse par la topologie, que l’on ne peut guère comparer qu’à la marche triomphale de l’idée de groupe à travers toutes les mathématiques ^{[cf. ALGÈBRE]}. De même que dans ce dernier cas, il faut bien se persuader que cette introduction de nouvelles «structures» mathématiques n’a pas eu pour motif un vain désir de généralisation gratuite, mais bien la constatation que ces nouvelles idées conduisaient naturellement à des méthodes d’attaque plus simples, plus souples et plus puissantes pour de nombreux problèmes classiques.

7. Géométrie différentielle

Une des origines du calcul infinitésimal avait été l’étude des courbes planes (tangente, courbure, rectification, etc.), et un de ses succès au XVIII^e siècle fut l’étude analogue des courbes gauches et des surfaces. Mais les résultats obtenus étaient relatifs à la position de la courbe ou surface dans l’espace (autrement dit, faisaient intervenir des points de l’espace non sur la courbe ou la surface) et n’étaient invariants que par les déplacements de l’espace ambiant; en d’autres termes, c’étaient des propriétés de la courbe ou de la surface considérées comme des corps rigides. Carl Friedrich Gauss paraît être un des premiers qui se soient posé le problème de la recherche des propriétés d’une surface qui soient invariantes par une déformation conservant les longueurs (où en quelque sorte on considère la surface comme un tissu inextensible; il ne faut pas confondre cette notion avec celle de déformation topologique, où il faut au contraire imaginer la surface comme un tissu élastique ). Un des plus célèbres résultats obtenus par Gauss est que, dans une telle déformation, il y a conservation de la courbure totale de la surface en chaque point.

Les propriétés locales considérées par Gauss peuvent encore être caractérisées comme celles qui ne dépendent que de l’expression du «ds ²» de la surface, ds ² = Edu ² + Fdudv + Gdv ² à l’aide de «coordonnées locales» u , v ; d’où la conception (qui a peut-être aussi son origine dans les travaux de Gauss sur la géodésie) d’une surface considérée in abstracto (indépendamment de tout «plongement» dans l’espace), donnée par un certain nombre de «cartes», homéomorphismes d’une portion de surface dans un plan (où les coordonnées u , v de l’image d’un point de la surface sont dites «coordonnées locales» du point); on sait qu’en général il n’est pas possible, pour des raisons «topologiques», de définir une seule carte pour la surface (par exemple, pour une sphère il en faut au moins deux); dans chaque carte, il faut ensuite se donner l’expression du ds ²à l’aide des coordonnées locales.

Lorsque, après 1845, on se fut familiarisé avec les espaces à n dimensions pour n 礪 3, un grand pas en avant fut l’extension de cette idée de «surface intrinsèquement définie» aux «espaces de Riemann» à un nombre quelconque de dimensions; la fin du XIX^e siècle et le début du XX^e siècle virent un brillant développement de ces idées avec l’exploitation des ressources du calcul tensoriel (cf.algèbre LINÉAIRE ET MULTILINÉAIRE), et les théories de mathématiques pures ainsi développées devaient peu après servir de substrat à la relativité générale. Mais en l’absence de conceptions topologiques assez élaborées, ces études restaient obligatoirement de nature locale (c’est-à-dire qu’en fait on ne regardait que ce qui se passait dans une carte). Ce n’est qu’après 1900 qu’on est parvenu à donner une définition globale satisfaisante d’une «variété différentielle», en formulant mathématiquement de façon précise l’idée intuitive de «recollement» de cartes; du coup, on s’est aperçu qu’il faut soigneusement distinguer cette notion de celle d’«espace de Riemann» (ou mieux «variété riemannienne»); cette dernière correspond à une variété différentielle sur laquelle on s’est donné une structure supplémentaire, un ds ²permettant de définir la notion de longueur et les notions géométriques qui s’en déduisent; et sur une même variété différentielle on peut définir en général une infinité de ds ² qui ne se déduisent pas les uns des autres par une isomorphie de la variété différentielle ^{[cf. GÉOMÉTRIE DIFFÉRENTIELLE CLASSIQUE]}.

Ce sont aussi les outils topologiques nouveaux forgés par le développement de la topologie algébrique qui ont permis, depuis 1940 environ, d’attaquer avec succès les problèmes globaux sur les variétés différentielles (cf. TOPOLOGIE - Topologie différentielle).

8. Groupes de Lie et espaces fibrés

Vers le milieu du XIX^e siècle, à côté des groupes de permutations d’ensembles finis, introduits au début du siècle par Cauchy et Galois (cf. GROUPES [Mathématiques]), on est peu à peu amené, dans des problèmes de géométrie, ou en vue d’intégration d’équations différentielles ou aux dérivées partielles, à considérer des groupes dont les éléments sont des transformations d’un espace Rⁿ ou d’une portion de cet espace, la loi du groupe étant (comme pour les permutations) la composition des transformations; en général, ces groupes sont formés d’une infinité de transformations, dépendant de paramètres qui varient «continûment». Par exemple, les homothéties:

de l’espace Rⁿ , de rapport t 0, forment un groupe dépendant du seul «paramètre» t. Les transformations orthogonales de R³, c’est-à-dire les transformations linéaires conservant la distance euclidienne (cf. formes QUADRATIQUES) forment un groupe de transformations:

où la matrice:

doit vérifier la relation ^t U 練U = I (matrice unité); ces relations entraînent que U dépend de trois paramètres.

D’une façon générale, les transformations d’un groupe seront de forme S^t : x 料 f (x, t ), où x varie dans une variété différentielle M, le «paramètre» t dans une variété différentielle G et f est une application différentiable de M 憐 G dans M (dans le premier exemple précédent, G est l’ouvert R 漣0 complémentaire de 0; dans le second, G est la sous-variété de R⁹ formée des matrices orthogonales).

Puisque les transformations S^t doivent former un groupe, on doit avoir S^t S^t = S^t , où t = g (t, t ), g étant donc une application différentiable de G 憐 G dans G, qui définit sur G une loi de groupe. Une variété G munie d’une loi de groupe différentiable est appelée groupe de Lie réel (on peut définir de même des groupes de Lie complexes en partant de variétés analytiques complexes). La découverte fondamentale de Lie dans la théorie de ces groupes est que leur structure «infinitésimale» les détermine dans une très large mesure. De façon plus précise, en prenant sur G des coordonnées locales au voisinage de l’élément neutre, le «paramètre» t correspond à un système de r nombres (t ^k ), et g (t, t ) est un système de r fonctions de 2r variables g ^k (t ¹, ..., t ^r , t ¹, ..., t ^r ); la connaissance des dérivées des g ^k au point correspondant à l’élément neutre (on peut supposer que c’est le point de coordonnées locales (0, ..., 0)) jusqu’au second ordre détermine complètement leurs développements de Taylor (et, en fait, par un choix convenable des coordonnées locales, on peut même faire en sorte que ces développements soient convergents au voisinage de l’origine). De plus, ces valeurs des dérivées d’ordre 諒 2 ne sont pas arbitraires, et lorsqu’on écrit les conditions qu’elles doivent vérifier, on obtient une structure purement algébrique appelée algèbre de Lie , dont l’étude équivaut donc à l’étude locale des groupes de Lie. Jusque vers 1925, on se limita à cette dernière; les travaux de Lie lui-même, puis de Killing et d’Élie Cartan mirent en évidence une classe particulière de groupes de Lie, les groupes semi-simples , que l’on peut déterminer de façon explicite et qui, ainsi que l’on s’en est peu à peu aperçu, jouent un rôle capital dans pratiquement toutes les parties des mathématiques. Avec les mémoires célèbres de H. Weyl en 1925 commence la théorie des groupes de Lie sous leur aspect global, développée ensuite par É. Cartan lui-même et une pléiade de mathématiciens de la génération suivante; il est remarquable qu’ici encore, tout au moins pour les groupes semi-simples connexes, la seule connaissance de l’algèbre de Lie face=F9828 g du groupe permette de décrire globalement tous les groupes de Lie qui admettent face=F9828 g pour algèbre de Lie (y compris leurs invariants topologiques).

L’étude des groupes de Lie globaux a bénéficié des résultats de la géométrie riemannienne; mais inversement, grâce aux travaux d’Élie Cartan, elle a permis de créer des méthodes d’une extraordinaire fécondité aussi bien dans l’étude des propriétés locales que dans celle des propriétés globales des variétés différentielles et des variétés riemanniennes, reposant sur la notion d’espace fibré. Il s’agit de variétés différentielles E qui sont réunion de «fibres» deux à deux sans point commun, deux à deux isomorphes, et formant une «famille différentiable» F^t , paramétrée par une autre variété, la «base» B. L’exemple le plus simple est une surface réglée où B est une courbe et les F^t des droites; parmi les exemples les plus importants sont les espaces fibrés des vecteurs tangents à une variété, forme moderne de l’idée d’«élément de contact» très étudiée par Lie et son école; pour une surface S, le fibré T des vecteurs tangents a S pour base et les fibres sont les plans tangents à S, de sorte qu’on a une variété de dimension 4. La «méthode du trièdre mobile» utilisée par Ribaucour et Darboux pour l’étude des surfaces plongées dans R³ revient à associer à l’espace fibré T un autre espace fibré de base S, où cette fois la fibre en chaque point est l’espace des trièdres orthonormés ayant pour sommet ce point. La théorie des groupes entre alors par le fait que le groupe orthogonal opère sur chaque fibre de ce dernier espace, et c’est en considérant la méthode du trièdre mobile sous cet aspect que É. Cartan a pu la généraliser dans sa grande théorie des «connexions», où le groupe orthogonal peut être remplacé par un groupe de Lie quelconque ^{[cf. GÉOMÉTRIE DIFFÉRENTIELLE CLASSIQUE]}.

L’idée qui avait permis à Lie de fonder sa théorie avait été, partant des groupes de transformations d’une variété M, de considérer le groupe en lui-même en faisant abstraction de son «action» sur M; mais il va de soi que l’étude des groupes de transformations reste un problème capital dans les mathématiques modernes. Un groupe de Lie, même aussi banal que le groupe additif des nombres réels, peut «opérer» dans une variété de façon très compliquée (cf. théorie ERGODIQUE); on ne peut donc espérer obtenir de résultats substantiels dans l’étude des groupes de transformations qu’en faisant des hypothèses restrictives de divers types.

L’une de ces hypothèses simplificatrices est la transitivité du groupe; les variétés sur lesquelles un groupe de Lie G agit transitivement sont ce qu’on appelle les espaces homogènes du groupe, et on montre que leur étude équivaut à celle des sous-groupes fermés K de G; un des cas les plus importants est celui des espaces symétriques , qui correspond au cas où G est semi-simple et K compact, et dont la théorie a été créée de toutes pièces par É. Cartan.

9. Représentations linéaires des groupes de Lie; analyse harmonique

Un autre type de groupe de transformations est fourni par le cas où la variété où opère le groupe est un espace vectoriel complexe E, et où les transformations sont linéaires ; lorsqu’un groupe G agit de cette façon sur E, on dit encore qu’on a une représentation linéaire de G.

L’intérêt se concentre ici sur les représentations irréductibles , c’est-à-dire telles qu’aucun sous-espace vectoriel de E, distinct de E et de0, ne soit invariant (globalement) par G; les deux problèmes principaux sont de déterminer toutes les représentations irréductibles, puis de «reconstituer» les représentations linéaires générales à l’aide des représentations irréductibles.

Lorsque l’on se borne aux représentations linéaires dans des espaces vectoriels E de dimension finie , le problème est essentiellement de nature algébrique, même pour les groupes de Lie (en se ramenant à considérer un problème analogue pour les algèbres de Lie); en ce qui concerne les groupes de Lie semi-simples, le problème a été entièrement résolu par Élie Cartan.

L’analyse intervient essentiellement par contre lorsqu’on considère des représentations linéaires dans des espaces fonctionnels E. Par exemple le groupe orthogonal de R³ opère linéairement sur l’ensemble E des fonctions complexes continues définies sur la sphère S de centre O et de rayon 1: si f est une fonction continue dans S, pour toute matrice orthogonale U, la fonction x f (U^-1 x ) sur S est encore continue, et si on la désigne par Uf , l’application f Uf est linéaire ; on définit ainsi une représentation linéaire du groupe orthogonal dans E.

Cette représentation (étendue à des espaces fonctionnels plus vastes) est précisément celle qui se trouve à la base de la théorie quantique des configurations électroniques des atomes (cf. mécanique QUANTIQUE). Mais, comme l’a le premier reconnu É. Cartan, l’étude de ces représentations linéaires «de dimension infinie» est aussi étroitement liée à de nombreuses questions d’analyse, notamment à la théorie de l’équation de Laplace et des «fonctions spéciales» qui s’y rattachent (fonctions sphériques, fonctions de Bessel, de Legendre, etc.). Elle fait encore à l’heure actuelle l’objet de nombreuses et profondes recherches et ne peut être considérée comme achevée que pour deux types particuliers de groupes, les groupes compacts et les groupes commutatifs.

La structure des groupes de Lie commutatifs est triviale, puisque les seuls groupes de Lie commutatifs connexes sont des produits de groupes égaux au groupe additif R ou au groupe (compact) multiplicatif U des nombres complexes de valeur absolue 1. De même il est très facile de déterminer les représentations linéaires irréductibles de ces groupes. Elles sont nécessairement de dimension 1, et leur détermination se ramène à trouver les caractères du groupe G considéré, c’est-à-dire les homomorphismes continus de G dans U: pour G = R, ce sont les fonctions x 料 e ⁱ size=1^﨡^x ( 﨡 réel) et pour G = U, les fonctions 﨡料﨣ⁿ (n entier positif ou négatif). La question intéressante ici est la «reconstitution» des représentations linéaires générales à l’aide des caractères; on constate que ce n’est autre chose, pour G = U, que la théorie classique des séries de Fourier , et, pour G = R, que l’intégrale de Fourier , d’où le nom d’analyse harmonique ou de théorie de la transformation de Fourier qu’on lui donne dans le cas général. Son rôle en analyse fonctionnelle (notamment dans la théorie des équations aux dérivées partielles) n’a cessé de grandir, surtout depuis que la théorie des distributions a considérablement élargi son champ d’application.

Conclusion

Nous avons au début parlé de diversification, et le lecteur aura pu voir à quel point elle est considérable; mais il aura sans doute aussi remarqué les liens, parfois tout à fait inattendus, qui ont été découverts entre toutes les parties de l’analyse, si éloignées qu’elles puissent paraître. C’est une des manifestations de la tendance caractéristique de la mathématique moderne, la recherche, sous le foisonnement toujours plus débordant de résultats d’apparence très divers, de l’unité profonde conférée par quelques grands types de structure.

Encyclopédie Universelle. 2012.