PROPORTION
Le terme proportion désigne un concept mathématique qui appartient à l’héritage grec et dont l’application s’étend à tous les savoirs quantifiables. «Cette partie, écrivait justement le père J. Prestet dans ses Élémens de mathématiques (1675), est si vaste, si féconde et ses usages ont une telle étendue dans la plupart des sciences qu’il n’y en a peu qui puisse estre expliquée sans elle.» En fait, ce concept dégénère souvent dans le langage commun, et le prestige de sa fécondité dans les sciences mathématisables l’a parfois fait utiliser présomptueusement dans certaines théorisations. Tel est bien le cas des esthétiques mathématiques dont on s’occupera principalement dans la première partie de cet article, la notion de proportion en architecture étant l’objet de la seconde.
L’ouvrage bibliographique publié par Hermann Graf en 1958 contient deux cents titres portant sur la proportion. Même si l’on était convaincu, comme certains architectes, qu’il s’agit là d’un débat purement académique, il n’en reste pas moins un problème, celui d’expliquer la patience des uns à chercher le secret de beauté des édifices antiques dans des tracés régulateurs , la fébrilité des autres à sous-tendre l’aspect de leurs projets par une règle («le choix d’un tracé régulateur est un des moments décisifs de l’inspiration, l’une des opérations capitales de l’architecture» a écrit Le Corbusier); il faudrait même expliquer l’ardeur de ceux qui – comme Claude Perrault, l’architecte de la colonnade du Louvre – veulent nier l’intérêt de la proportion en architecture en raison des déformations optiques que le point de vue changeant des spectateurs fait subir à la réalité géométrale du projet et auxquelles Vitruve apporte ces corrections qu’il nomme «temperaturae ». Une phénoménologie de la proportion pourrait donc s’envisager ou encore une psychanalyse de ce désir de forcer les bâtisses à livrer le secret d’une beauté divinement tacite. Mais cela risquerait de nous mener hors de l’architecture. Il nous importera plutôt ici de cerner la proportion comme concept spécifiquement architectural , de lui donner un sens architecturologique plutôt que de l’approcher d’une manière phénoménologique, psychanalytique, ethnologique ou historique. Le problème majeur est alors surtout de distinguer la proportion architecturale de la proportion mathématique ou de la proportion musicale avec lesquelles elle est encore en confusion historique et épistémologique. Cherchant à construire un concept entrant dans un système de connaissance scientifique de l’architecture, on s’apercevra que celui de proportion ne peut être éclairé que par un autre concept qui lui est extérieur et l’englobe, celui d’échelle . Dans l’histoire de l’architecture, la notion d’échelle fait son apparition significativement au XIXe siècle. Si elle commence à prendre corps et à devenir une réalité pratique dans le Modulor de Le Corbusier, dernier en date des systèmes de proportions, il reste à donner à cette notion le statut de concept dans une théorie scientifique de l’architecture.
La proportion comme principe esthétique
La définition et l’usage
En toute rigueur, conformément à Euclide, la proportion, c’est l’équivalence de deux rapports entre des grandeurs homogènes; elle est donc composée essentiellement de quatre termes: le second et le troisième sont dits moyens par opposition aux extrêmes . Quand les deux moyens sont égaux la proportion n’offre plus que trois termes dont la séquence engendre une progression . Les mathématiciens grecs ont défini et classé des relations dont l’ensemble constitue la théorie des médiétés . Archytas fait état de trois proportions, l’arithmétique, la géométrique et la subcontraire ou harmonique. Dans l’arithmétique, chaque terme conséquent surpasse de la même quantité son antécédent; dans la géométrique à trois termes, le premier est au second ce que le second est au troisième; quant à la subcontraire, selon la définition de Porphyre, elle est réalisée si «le premier terme excédant de quelque quotité de lui-même le second, celui-ci excède le troisième par la même quotité du troisième». Donc, si a , b et c sont en progression subcontraire, la relation a = b + a /n entraîne b = c + b /n ; d’où il résulte que a /c = (a 漣 b )/(b 漣 c ), ou 1/a + 1/c = 2/b .
Nicomaque et Pappus décrivirent par la suite un ensemble de dix relations fonctionnelles entre trois termes, incorporant les trois types précédents. Une autre relation traditionnelle, particulièrement valorisée, associe quatre termes, selon une loi qui combine les proportions harmonique et géométrique; par exemple, dans la suite 12, 9, 8, 6. Cette forme, qualifiée par Jamblique de musicale, passait pour être d’origine babylonienne et aurait été introduite en Grèce par Pythagore.
Le calcul des médiétés ne procure pas nécessairement des expressions rationnelles; de même que la diagonale du carré est incommensurable au côté, un rapport comme la «section d’or» est arithmétiquement irrationnel; il s’agit de la proportion continue présente dans le partage d’un segment en moyenne et extrême raison, telle que a /b = (a + b )/a . La valeur du rapport a /b qui satisfait à la condition précédente est invariablement (1 + 連5)/2, soit, en première approximation, 1,618...
Dans son acception stricte, l’idée de proportion suppose une opération ternaire: ce qui est manifeste dans le calcul des médiétés qui refère un rapport à une relation nécessaire entre ses termes se dissimule dans l’appréciation des rapports mesurés sur des objets concrets. La relation métrique entre une partie et le tout d’une organisation naturelle ou artificielle entraîne la corrélation des parties entre elles. Ce qui est organiquement défini n’est pas déterminé dans un unique rapport. Le langage usuel entérine en quelque sorte ce réquisit, jusque dans ses impropriétés, lorsque, par exemple, il dit d’une grande bâtisse qu’elle a de «vastes proportions», étant entendu que la taille humaine est prise pour référence (ce qui implique la notion d’échelle ).
Au demeurant, l’incorrection évidente du langage parlé, dans les matières de proportion, ne nuit pas, loin de là, à sa valeur expressive. Un exemple trivial, mais bien significatif, en rend compte. Un fabricant de poudre à récurer énonçait naguère que son produit «bichlorellisant détache et désinfecte deux fois plus vite». Un tel message est doublement abusif dans un usage spécieux du concept de proportion: tout d’abord, «bichlorellisant» n’a aucun sens positif en français et ne fait qu’évoquer par un vague mimétisme la langue chimique, qui, on le sait, règle son code préfixal d’après les quantifications d’un système proportionnel généralisé à l’ensemble des combinaisons. Ensuite, la vitesse invoquée de l’action du produit n’est référée, pour des raisons évidentes, à aucun terme de comparaison, si bien que le relatif est donné ici pour un absolu fascinant. Cette formulation vicieuse illustre bien la corruption sémantique qui enchérit sur l’élision, en termes de rapports, fréquente lorsqu’il s’agit de décrire une proportion. La raison numérique, mal explicitée ou illégitime, est alors prise pour une qualité substantielle, dans un avatar tardif de la pensée pythagoricienne.
Le pythagorisme pur
Le concept de proportion dérive du concept d’ordre dans sa détermination numérique. L’axiome primordial de la doctrine pythagoricienne: «Tout est arrangé selon le nombre» profère une norme dont la compétence étendue à l’univers en règle le mode de composition; l’essence de la réalité physique s’identifie au nombre rationnel et la beauté comporte des clefs arithmétiques. Cette conviction s’appuyait sur la découverte capitale que les rapports numériques simples expriment les intervalles musicaux d’octave, de quinte et de quarte. La nature paraissait répondre à la pensée mathématique et la beauté à toutes deux. L’ambition d’appareiller la diversité des apparences sous le régime d’une constitution arithmétique marquera dès lors l’histoire des théories esthétiques. Une fois formulées les lois numériques de la beauté acoustique, elles furent généralisées à toutes les représentations. Le pythagorisme, cautionné par Platon dans le Timée , domina les spéculations sur l’harmonie de la nature comme des produits de l’art. Augustin reconnaissait les rapports pythagoriciens dans le mètre poétique des Anciens. L’astronomie fut «harmonisée» sous le régime de la «musique des sphères», et le postulat de la perfection arithmético-musicale de la machine céleste inspirera Kepler. À la suite de Boèce, les «musiciens» médiévaux étendirent leur compétence jusqu’à la vie morale (la vertu étant considérée comme moyenne «harmonique» entre les extrêmes des vices opposés) et rejoignirent, en quelque sorte, dans la théorie du mélange harmonieux des tempéraments l’héritage hippocratique et galénique de la juste proportion, caractéristique de la santé physique. Dans leurs traités qui commencent par l’harmonie cosmique, ces musiciens en viennent à reléguer l’harmonie auditive et la musique instrumentale dans les derniers chapitres.
La physique du Timée fait une grande part aux «vertus» formelles de figures régulières, et notamment des cinq corps dits platoniciens, dont la théorie constitue une sorte de prolongement géométrique du pythagorisme arithmétique. On rencontre dans deux de ces corps le rapport irrationnel de la section d’or dont l’origine n’est pas pythagoricienne; il fut sans doute utilisé au Moyen Âge dans le dessin des édifices. Mais ce furent surtout aux proportions musicales proprement dites que recoururent, à la suite d’Alberti, les architectes de la Renaissance soucieux de composition harmonieuse.
L’expérience tant soit peu attentive de la beauté formelle disqualifie les prétentions du pythagorisme. Croire que les mêmes lois numériques ou géométriques régissent la nature et la beauté, optique ou acoustique, trahit une impavide volonté de simplification. La matière des œuvres, l’individualité du spectateur et les circonstances culturelles sont allégrement omises dans une représentation qui, si elle était fondée, procurerait aisément de sûres recettes. Cependant, si naïf qu’il soit, le pythagorisme généralisé a pu s’appuyer sur l’incontestable valeur esthétique du module et du rythme. On est toujours satisfait quand une quantité discrète quelconque peut être sentie comme un commun dénominateur de plusieurs autres quantités de même espèce dans un ensemble soumis à notre appréciation esthétique. Les constructions géométriques, qu’elles soient «pures» de toute finalité technique ou destinées à la projection architecturale, procurent aisément ce genre de satisfaction. En revanche, les rapports de la modularité à la figure humaine sont moins évidents, la conspiration entre forme organique et grille métrique n’est jamais parfaite. Et, dans leur analyse des canons de proportion, les érudits contemporains purent distinguer des classes théoriquement exclusives, qui parfois, néanmoins, sont équivoques dans leur réalisation; si Erwin Panofsky oppose les systèmes «objectifs» – appliqués au corps même – aux systèmes «constructifs» en acte dans les simulacres graphiques, André Chastel et Robert Klein distinguent canons arithmétiques et canons géométriques, sans prétendre à une totale rigueur de classement.
Normes idéales et normes statistiques de proportion
L’explication métrique du corps a sa source littéraire dans le livre III de Vitruve (De architectura ); il y énonce, avec la division arithmétique de l’organisme, la proportion de chaque membre avec le tout, et préconise la composition analogique des édifices: «Jamais un bâtiment ne pourra être bien ordonné [...] si toutes les parties ne sont, les unes par rapport aux autres, comme le sont celles du corps d’un homme bien formé» (III, I). La théorie arithmétique du corps proportionné fut une référence constante pour les sectateurs de l’harmonie universelle. Ainsi Augustin développe-t-il l’analogie métrique entre le corps humain et l’Arche, vaisseau du salut (Civitas Dei , XV, XXVI), et, dans sa quatrième vision, Hildegarde de Bingen fait participer les proportions corporelles aux connivences cosmiques. La définition des formes humaines idéales fut même un projet proprement philosophique lorsque la tradition pythagorico-platonicienne rencontra les préoccupations scientifiques de l’art du Quattrocento: Marsile Ficin invoque les proportions dans son édition du Banquet (1484). Elles soutiennent l’argumentation du De divina proportione de Pacioli (1509), de l’Harmonia mundi de Francesco di Giorgio (1525) et de l’Occulta Philosophia de Cornelius Agrippa (1533), tous traités qui ne contribuèrent pas peu à revaloriser les canons régulateurs du «microcosme» corporel. L’espérance d’une norme physique et esthétique absolue se sépare d’attitudes qui, rattachées encore, de quelque manière, à l’inspiration vitruvienne, visent à codifier des règles d’atelier ou à définir des normes anthropométriques. Cette dernière tendance est illustrée par Alberti dans son De statua lorsqu’il divise la taille en unités indépendantes de la structure organique et exprime les dimensions des membres en multiples de cette unité – à la différence des vitruviens de stricte observance qui les énoncent en fractions de la hauteur totale. Les enquêtes multipliées sur le vif ne pouvaient que relativiser l’idée de canon, en faisant ressortir les écarts entre divers types de beauté physique: Michele Savonarola avait reconnu à cet égard le poids des conditions géographiques et physiologiques, bien qu’il tînt pour la déductibilité des proportions idéales.
Le pythagorisme organiciste
En introduisant des idées biologiques dans les spéculations esthétiques on écarte les superstructures métaphysiques qui grèvent le pythagorisme orthodoxe et l’on s’achemine vers une interprétation fonctionnaliste. Le sentiment de la beauté procéderait alors de quelque parenté secrète entre les conditions de la perception et les objets; serait beau le spectacle des «membres et des autres choses aptes à atteindre leur fin», selon les termes de V. Danti dans son Trattato delle perfette proporzioni (1567). La tâche d’une esthétique fondée sur ces prémisses consisterait à formuler mathématiquement les conditions de «bonnes» structures ou fonctions organiques, et de les vérifier ensuite dans le cas de la beauté formelle. Les sectateurs du nombre d’or ont tenté quelques approches dans ce sens. On a fait grand cas de ce que ce rapport ou les figures qui le supportent peuvent être reconnus dans le mode d’insertion des feuilles sur les rameaux ou dans l’enroulement de certaines coquilles, voire dans les proportions du corps humain. Il s’agit là de considérations suspectes, car il est vain de prétendre vérifier la présence du nombre d’or en partant de grandeurs aussi mal définies que les mesures moyennes des membres de l’organisme humain; aussi at-on voulu justifier de telles supputations par des causalités fonctionnelles, en invoquant des lois d’optimum pour l’insolation des feuilles ou des lois de croissance pour les spires des coquilles. On a encore tenté de relier les déplacements des membres humains à des formes comportant la section d’or; von Laban a pu les inscrire dans l’icosaèdre platonicien; et le modulor de Le Corbusier est un essai un peu forcé, mais ingénieux et original, de lier deux séries de Fibonacci (où le rapport de deux termes successifs a pour limite le nombre d’or) aux dimensions d’habitat déduites des positions et des mouvements de l’homme.
Cette version organiciste du pythagorisme, plus prudente que la mystique, n’en appelle pas moins des objections: c’est beaucoup demander à notre «instinct» du beau que de réagir avec précision à certaines formes privilégiées de l’organisme bien constitué; le bon rendement des fonctions organiques n’inspire pas en toute circonstance un jugement esthétique positif. Le pythagorisme fonctionnel n’échappe pas plus que l’autre au postulat d’une harmonie préétablie entre nature et sentiment esthétique, et échoue devant la différence de ses matières particulières.
Pourtant, l’association de la beauté avec l’organique et le nombre ne peut être tenue pour insignifiante; elle répond au contraire à une exigence irrépressible de «justesse»; le beau formel apparaît toujours comme étant inexplicablement juste: une de ses plus antiques définitions attribuée à Polyclète se fondait précisément sur sa dépendance à l’égard de minimes transitions; et l’on peut encore citer Alberti dirigeant à distance une construction qui réclamait l’observance exacte de son dessin, car la moindre altération «désaccorderait toute cette musique»!
Modèles académiques et sentiment de justesse
Cependant, le sentiment de justesse allait trouver à s’exercer sur la comparaison des modèles et se nourrir des variations introduites par les grands maîtres. Le génie se donne ses règles, et l’éducation académique s’accomplira dans l’imitation d’œuvres prestigieuses données pour exemplaires de la «nature choisie» et du «beau idéal». Le classicisme renoncera à une théorie approfondie des canons. On se contentera dans les écoles de bien distinguer les morphologies propres aux divers âges et tempéraments, dans les deux sexes, tout en se référant aux antiques régulièrement valorisées. C’est ainsi que J. B. Corneille, après avoir averti que «les Proportions qui plaisent à tout le monde sont celles de figures antiques, dont le goust, la correction et la pureté ont une approbation générale», propose, tour à tour, les types de l’Hercule Farnèse, du Méléagre et de l’Apollon du Belvédère; mais, en sus des proportions exemplaires, il ne manque pas d’introduire le caractère comme ingrédient essentiel du beau (Les Premiers Élemens de la peinture pratique , 1684).
Au XVIIIe siècle, l’observation attentive du naturel donne à voir la grande variété des types humains selon les circonstances de la vie: «les mœurs occasionnent insensiblement des variétés physiques dans la constitution et dans le développement de la forme du corps», mais on s’avise opportunément, dans le même temps, que «le trop grand détail des mesures est sujet à erreurs» (Encyclopédie , d’après Watelet). À la même époque, Burke refusait que la beauté fût affaire de calcul et de géométrie et la concevait comme le produit exclusif et irrationnel d’une sensibilité subjective (Enquiry into the Origin of Our Ideas of the Sublime and the Beautiful , 1757). Si la proportion est, de droit, objet de mathématique, en revanche, elle tendra dans la langue des critiques à désigner une qualité qui informe globalement le jugement esthétique, savoir, comme la définit l’Encyclopédie , la «convenance du tout et des parties entr’elles dans les ouvrages de goût».
La quantification psychophysique
Au XIXe siècle, maint esthéticien se persuadera que le sentiment de justesse à l’égard des décisions formelles de l’artiste résulte de raisons objectives et formulables. Parmi les explications fonctionnelles mises en œuvre, il en est d’ordre psychophysique qui reposent sur la présomption selon laquelle il est légitime d’attribuer à divers éléments formels des coefficients caractéristiques de leur activité; des expériences faciles mettent en évidence nos diverses sensibilités au sens «montant» ou «descendant» de lignes obliques, aux valeurs de «solidité» d’une figure, aux «tensions» d’une rencontre de formes, aux «champs» induits par un signe, etc. La quantification de ces phénomènes n’est pas impossible, et le physiologiste Charles Henry, l’inspirateur de Seurat, a tenté une mathématisation de la «dynamogénie» de configurations simples. Depuis les symbolistes qui furent attentifs à tout ce qui prétendait expliquer les correspondances entre les sens, on a développé, avec plus ou moins de bonheur, des études d’esthétique expérimentale sous la domination théorique des psychologies à la mode: doctrine de la sympathie (Einfühlung ), psychologie de la forme (Gestalt ) ou du comportement (behaviorism ), voire la phénoménologie de la perception. Mais, dans de telles recherches, les présupposés de l’esthétique mathématique sont effacés. Le calcul peut bien fournir des moyens de présenter et d’analyser les résultats, il n’est plus censé dévoiler l’essence de la beauté. L’objectivisme, pythagoricien ou organiciste, est abandonné, cependant que l’attention se porte sur les réactions du moi sujet, c’est-à-dire d’une donnée sujette de la psychologie différentielle et tributaire des conditionnements historiques. Au mieux peut-on espérer composer de la sorte une esthétique psychologique partiellement mathématisée.
L’art combinatoire
On conçoit que ce principe d’unité, parce que complexe, s’accommode mal des tentatives frustes d’analyse du beau par l’application spécieusement distincte de grilles schématiques qui seraient censées dévoiler quelque «géométrie secrète» des œuvres. Si beaucoup d’artistes ont esquissé leurs compositions en s’aidant de stéréotypes, ce fut sans conséquence pour la beauté de leur ouvrage. D’où la vanité de telles dissections.
En revanche, on peut reconnaître dans le travail d’artistes contemporains une soumission délibérée à des stéréotypes de composition. Celle-ci est intégralement déductible de formes abstraites, l’œuvre consistant en permutations et développements d’éléments discrets d’un thème. Le sujet artistique intervient alors dans la sélection d’éléments sensoriels dont l’apparition est l’effet d’une programmation. À divers degrés, les ouvrages de Schöffer, de Vasarely, de Morellet, de Molnar, parmi d’autres, prennent pour seule matière un développement thématique, leur critère est à chercher dans les théories de l’information; mais en éliminant quantité de matières associées à l’expérience de la beauté formelle, ils tournent le dos à l’esthétique; leur domaine est dans l’exhibition des combinaisons d’un répertoire simplifié; le pur devient le pauvre. On sent tout le ridicule de justifications que se donnent parfois les pratiquants de cet art, quand ils invoquent la possibilité pour l’ordinateur de prendre en charge l’analyse et la rectification des œuvres artisanales (Molnar déclarait au cours d’un entretien radiodiffusé avec un commis voyageur de l’informatique que l’on pourrait «faire du Cézanne mieux»).
Le pythagorisme renversé
Quand l’art donne à voir tel modèle de distribution il crée un être mathématique, tout en continuant à se prétendre art. Que cette revendication soit justifiée ou non est une question à débattre. Mais l’expérience apprend que des objets mathématiques peuvent être beaux; maints ouvrages d’Antoine Pevsner, Naum Gabo, Max Bill ressemblent singulièrement à des modèles spatiaux de fonctions mathématiques. Cette ressemblance dissimule un rapport nouveau: dans une sorte de pythagorisme renversé l’art pasticherait la beauté des mathématiques, au lieu de chercher dans les nombres les raisons de ses formes et de sa beauté. On peut s’interroger sur la valeur d’un tel mimétisme: l’émotion esthétique produite par la pensée mathématique peut-elle être isolée du processus même de cette pensée? En d’autres termes, les figures mathématiques réalisées et les objets similaires conservent-ils la beauté propre à la pensée qui les engendre? L’art, dans l’affirmative, peut-il se satisfaire de la reproduction d’une telle beauté objective? On serait tenté de tracer ici des limites à la valeur de telles entreprises; sans pourtant nier la fonction phatique des opérations du pythagorisme renversé: elles donnent des leçons de pureté, et disent la nature intellectuelle du beau.
Mais pas plus que toutes les tentatives précédentes, ces opérations mimétiques n’explicitent définitivement une raison mathématique du beau. Les essais d’esthétique mathématique échouent toujours quand on les met à l’épreuve d’une critique attentive; d’autant que la pensée esthétique peut encore raisonnablement théoriser en récusant toute approche mathématique du beau.
Proportion et mise à distance
Il y a peut-être lieu, en dernière analyse, de mettre en question le sens des échecs, discrets et répétés, des esthétiques mathématiques, c’est-à-dire de l’ensemble discursif qui comprend la formation du concept de proportion (avec ses attaches symboliques), son application au déchiffrement du beau et la compétition subséquente de théories qui s’y rapportent. La proportion en est l’argument primordial toujours à l’œuvre pour instrumenter et rationaliser la faculté de miniaturisation. Cette opération abstraite estampille un mode de représentation, et toute une attitude à l’égard de ses objets. En poussant l’interprétation à l’extrême on peut se demander si le respect porté à la proportion consacrée ne dénoncerait pas la tentation occidentale de réduire l’appropriation de l’univers – nature plus art – à un ordre en quelque manière haineux de la vie.
L’édition de 1611 des Due Regole della prospettiva practica de Vignole, due aux soins d’E. Danti, est ornée d’une singulière gravure, en pleine page, que nous reproduisons. Elle figure expressément une technique de mise en miniature d’un fragment choisi de la nature. Un modèle féminin est réduit en simulacre plan par un dessinateur qui ne le voit pas; il obéit aux consignes répétées d’un observateur qui détaille les contours au moyen d’un instrument de visée dont les configurations successives se trouvent réglées selon un mode de coordonnées cartésiennes. Cette image rappelle les figures où Dürer montre un artiste observant son motif au travers d’une trame verticale aux mailles carrées qui lui sert de guide dans la délinéation de l’image. Mais, ici, la gravure illustre la décomposition, entre deux opérateurs, des gestes qui conspirent à la figuration. La médiation supposée de la parole réunit et coordonne la séparation fonctionnelle du regard de l’un vers l’objet et du regard de l’autre vers l’image, que supporte une double instrumentation; un ensemble technique, transducteur de proportions, assujettit à la grille du dessin les proportions corporelles du modèle, c’est-à-dire un sujet humain qui consent d’être institué objet par le fait de l’appareillage et des conventions de son bon usage. Il y a là comme une allégorie de l’empire de la théorie artistique avec toutes ses corrélations morales: la femme désirable est, bel et bien, mise à distance pour être convertie en simulacre immobilisé derrière une grille. Le discours sublimant de la technique fait écran aux impulsions comme aux indifférences du désir dont il altère et diffère les réalisations possibles. La vie, en ce qui la symbolise ici, une jeune femme savoureuse, se trouve interpellée, mais fixée dans le compromis d’une figuration à laquelle l’ordre monotone de la mathématique donne ses règles et des critères de jugement. La soumission aux normes techniques de la raison mathématique ne serait-elle pas le signe d’un idéal ascétique de rationalité qui contient à distance les représentations du désir, à la frontière de l’illusoire consenti? Cette préférence axiologique n’apparaît-elle pas sous la plume du savant jésuite Prestet, quand à l’alternative: «Sommes-nous plutôt faits pour vivre, ou nous lier étroitement avec les hommes, que pour penser, ou pour nous unir à la vérité?» il répond par cet arrêt inexorable: «Nous cesserons de vivre et nous penserons toujours.»
Architecture, proportion et échelle
La proportion architecturale analogique des proportions mathématique et musicale
Pour Vitruve, premier théoricien de l’architecture, celle-ci est une science. Certes la pensée de Vitruve est éloignée du statut scientifique que l’épistémologie moderne confère aux diverses sciences; déjà Newton s’étonnait de l’incompréhension totale qu’il avait du discours de Vitruve et pensait que tous les mots que celui-ci utilisait avaient changé de sens (P. Schoffield). Aussi la lecture des passages des Dix Livres d’architecture concernant la proportion ne donnet-elle pas au lecteur contemporain un grand sentiment de clarté: «La proportion est le rapport que toute l’œuvre a avec ses parties, et celui qu’elles ont séparément, comparativement au tout, suivant la mesure d’une certaine partie. Car de même que, dans le corps humain, il y a un rapport entre le coude, le pied et la paume de la main, le doigt et les autres parties, ainsi dans les ouvrages qui ont atteint la perfection, un membre en particulier fait juger de la grandeur de toute l’œuvre [...]. L’ordonnance d’un édifice consiste dans la proportion qui doit être soigneusement observée par les architectes. Or la proportion dépend du rapport, que les Grecs appellent analogie ; et par rapport il faut entendre la subordination des mesures au module dans tout l’ensemble de l’ouvrage, ce par quoi toutes les proportions sont réglées; car jamais bâtiment ne pourra être bien ordonné, s’il n’a cette proportion et ce rapport et si toutes les parties ne sont, les unes par rapport aux autres, comme le sont celles du corps d’un homme bien formé.» Mais si l’architecture peut être objet de science, le premier problème de cette science est de trouver cet objet. En attendant, la proportion n’est en architecture qu’une notion qui procède par analogie, ce que montrent le «de même que» et le «comme» de Vitruve, analogie avec la proportion musicale, analogie avec la proportion du corps humain.
C’est cette analogie qui opère lorsque les architectes de la Renaissance italienne transposent à l’espace les vertus harmonieuses et bienfaisantes des proportions musicales: Francesco di Giorgio, expert musical, est appelé pour juger de la qualité des dimensions de certains projets architecturaux et Alberti écrit: «Les proportions par lesquelles l’harmonie des sons touche notre oreille sont exactement les mêmes qui plaisent à nos yeux et à notre esprit». (Rudolf Wittkower). Ici encore la proportion réside moins dans les proportions mathématiques qui fixent les longueurs suivant lesquelles les cordes vibrent harmonieusement, ou encore les proportions des dimensions que Palladio donne aux diverses parties de ses villas, que dans la pensée analogique du même . Aujourd’hui encore il est significatif que Xenakis, musicien et architecte, qui a travaillé notamment chez Le Corbusier au Modulor et à son «mur musical», écrive à propos de sa conception du pavillon Philipps à l’Exposition de Bruxelles: «Mes propres recherches musicales sur les sons à variation continue en fonction du temps me faisaient pencher pour des structures géométriques à base de droites.» L’architecture n’étant pas séparée comme spécificité dans les discours théoriques des architectes, la proportion relève à chaque époque de l’idéologie ou du système de pensée régnant et peut s’étudier dans son développement ainsi qu’il apparaît dans les travaux de Wittkower et de Panofsky. Ainsi, la pensée humaniste de la Renaissance est, selon Wittkower, déterminante pour la conception de l’architecture de cette époque. L’homme est à l’image de Dieu et en proportion avec lui. Par l’intermédiaire de l’esthétique musicale, l’architecte de la Renaissance utilise les propriétés mathématiques des rapports de rapports, analogie qui préside à la définition donnée par Euclide: «Le rapport est la relation qualitative en ce qui concerne la dimension entre deux grandeurs homogènes. La proportion est l’équivalence de rapports.» Dans cette «équivalence» se retrouve encore le «même» de l’analogie qui préside également à la loi du même dont Borissavliévitch voudrait faire une loi scientifique de l’architecture.
Scientificité de l’architecture
Deux obstacles épistémologiques s’opposent à une pensée scientifique de l’architecture. Le premier consiste à croire que l’espace réel de l’architecture est ou peut être l’objet d’une science de l’architecture. Car définir, cerner l’architecture comme partie de l’espace réel n’amène qu’à des discussions sur la limite réelle de cet espace architectural. Cela explique l’existence de livres tels que celui de Rudofsky Architecture sans architectes qui introduit dans le domaine de l’architecture des constructions vernaculaires, et même un baobab. Viser la définition de l’architecture dans l’espace réel ne peut donc qu’aboutir à des divisions idéologiques et culturelles: chacun sait que l’École des beaux-arts a longtemps considéré comme architecture réelle les seuls lieux antiques de la Grèce et de Rome.
Si l’on veut définir l’architecture comme objet de science, il est nécessaire de considérer la différence essentielle qui existe entre un baobab et une cathédrale: cette dernière a été projetée . Certes, la plupart des activités humaines sont le fruit d’un projet. Toutefois le projet de l’architecte est projet de l’espace, d’un espace réel; il est de réaliser l’espace. Si l’architecture est une certaine pensée de l’espace, le second obstacle épistémologique réside dans la nécessité de la différencier de cette autre pensée de l’espace qu’est la géométrie. La différence tient dans la taille , différence qui est de nature à étonner Socrate.
SOCRATE. – Mais ne peut-on copier le marsouin ou le thon eux-mêmes et piller directement la nature?
PHÈDRE. – Je le croyais naïvement, Tridon m’a détrompé.
SOCRATE. – Mais un marsouin n’est-il pas une sorte de navire?
PHÈDRE. – Tout change avec la grosseur. La forme ne suit pas l’accroissement si simplement: et ni la solidité des matériaux, ni les organes de direction ne le supporteraient. Si une qualité de la chose grandit selon la raison arithmétique, les autres grandissent autrement.
Ce passage de l’Eupalinos de Valéry montre comment, en architecture, à la différence de ce qui se passe en géométrie, lorsque l’échelle augmente, les proportions ne sont pas gardées. Lorsque Platon géomètre raisonne sur le tétraèdre, il le fait dans un espace idéal qui est celui de la géométrie, et la taille réelle du tétraèdre n’intervient pas dans son raisonnement. Par contre, l’invention par Bell des structures tridimensionnelles tétraédriques réside dans la réalisation dans l’espace d’une figure idéale . Ici la taille réelle intervient dans la pensée de l’architecte, et constitue l’échelle , premier concept spécifique de l’architecture. L’échelle est ce qui existe dans la pensée de l’architecte et n’existe pas dans celle du géomètre. Schéma idéaliste de la conception architecturale, la proportion fait de l’architecture l’analogique dans l’espace réel d’espaces non spécifiquement architecturaux mais idéaux. À la Renaissance l’édifice est un système clos dans lequel les mesures sont rapportées idéalement les unes aux autres, l’architecture se réduit à la géométrie du projet et la réalisation importe peu. Ainsi l’intérêt pour l’architecture se satisfait du seul examen de la représentation graphique des édifices de Palladio dans les Quatre Livres d’architecture . Cependant l’architecte réalise l’architecture, et pour cela il doit donner à l’édifice dont il a fixé les proportions une taille. Si le travail de proportions est proche de l’activité du géomètre, l’acte de réalisation architecturale tient dans le fait de donner à un bâtiment son échelle, sans laquelle l’édifice ne pourrait pas passer de l’idéalité à la réalité . Ce passage de l’espace mental de l’architecture à l’espace réel que règle l’échelle est précisément l’objet d’une connaissance qui n’est pas celle de l’espace architectural réalisé (objet sur lequel se porte l’intérêt des esthéticiens, des historiens d’art ou des archéologues qui prennent les mesures des édifices; de ce type d’activité relèvent en effet les prises de mesures effectuées si souvent sur les pyramides d’Égypte). L’objet d’une telle connaissance n’est pas non plus le tracé régulateur des édifices sur la planche à dessin, qui constitue une activité plus géométrique que spécifiquement architecturale de l’architecte. L’espace de cette connaissance est celui de la conception de l’architecture, et ses lois sont celles qui régissent le passage de l’espace idéal à l’espace réel.
Le Modulor de Le Corbusier
La définition du champ épistémologique de l’architecture, l’espace architecturologique, autorise à ne pas s’attarder sur les différents systèmes de proportion qui ont été utilisés en architecture suivant les époques. Ces études en effet intéressent celui qui, comme R. Wittkower, analyse les rapports entre l’architecture et la culture. Il nous importe plutôt ici de situer architecturologiquement le dernier système de proportion en date, celui de Le Corbusier, le Modulor.
Le rapport 1/1,618 utilisé par Le Corbusier pour créer une harmonie dans les édifices n’apparaît pas comme un progrès mais comme la simple reconduction de la divina proportione à laquelle le moine fra Luca Pacioli di Borgo consacra en 1509 un traité illustré par Léonard de Vinci. Cette proportion était elle-même la limite vers laquelle tendait la série de Fibonacci dans laquelle chaque terme est la somme des deux précédents (1 漣1 漣2 漣3 漣5 漣8 漣13 漣. . .; 8/13 = 0,618). Dans le Modulor de Le Corbusier chaque terme est aussi la somme des deux précédents. Ce qui permet autour des valeurs voisines une certaine possibilité de mise en congruence des dimensions. Mais précisément, c’est lorsqu’on change d’échelle que le Modulor est difficilement applicable car les valeurs éloignées du Modulor peuvent rarement être obtenues par des multiples de valeurs plus petites. Le passage ne peut pas
se faire par multiplication ou addition mais uniquement par proportion, à la différence de la série de Fibonacci. Cette différence contenue dans le Modulor entre le proche et l’éloigné serait, de fait, un phénomène d’échelle. Toutefois l’analogie règne dans le Modulor et la série transmet du petit au grand des rapports identiques, en quoi le Modulor reste bien un système de proportions qui ne différencie pas le grand du petit. Dans le Modulor, l’ambiguïté entre la proportion et l’échelle est à son comble. Et précisément, sur le plan historique, la nouveauté remarquable du Modulor tient au projet de relier ce système de proportion à l’espace réel. Reflet de l’humanisme de la Renaissance, l’«homme-le-bras-levé », qui mesure 1,83 m, est notion idéologique en même temps que représentation de la réalité: «Le Modulor en tant que «ruban gradué tenu dans la main» permet de «voir» ses dimensions, ce qui est d’importance primordiale. Le malheur du temps présent, c’est que les mesures sont partout tombées dans l’arbitraire et dans l’abstraction; elles devraient être chair, c’est-à-dire expression palpitante de notre univers à nous, l’univers des hommes, qui est le seul concevable à notre entendement», écrit Le Corbusier. D’où la contradiction à laquelle n’échappe pas le Modulor: les hommes ne mesurent pas tous 1,83 m. Elle réside en ce que Le Corbusier veut fabriquer en même temps un système de proportion et un système d’échelle. Or précisément ce qui caractérise la proportion est son caractère clos tandis que l’échelle est référence à un élément extérieur: échelle urbaine, échelle humaine, échelle économique. Pour prendre un exemple, les proportions d’une boîte d’allumettes ne permettent pas d’en apprécier la taille réelle, seule la référence à un élément extérieur au système de proportion de la boîte d’allumettes permet d’envisager la taille, la référence finale étant le corps. Dans cette limite congruente entre l’homme et le monde extérieur apparaît la notion d’échelle humaine. Au terme de quoi on peut considérer l’échelle ou les échelles comme les mesures d’espaces non architecturaux (économique, technologique, géographique ou urbanistique, etc.) auxquels l’architecte se réfère pour concevoir un espace architectural réalisable.
La contradiction du Modulor tient alors à ce que Le Corbusier cherche un système d’échelle-dimensionnement de l’espace réel alors que l’échelle est référence d’un espace à un autre espace et que sa caractéristique réside dans l’ouverture, au contraire de la proportion qui règle un système clos. Aussi peut-on penser que la proportion en architecture a correspondu à une conception idéaliste de l’architecture qui n’aurait pas de rapport au réel, si ce n’est par une échelle implicite.
Si le terme d’échelle est inexistant dans le discours de Vitruve, il n’en reste pas moins que son utilisation pratique y est sous-jacente. L’échelle apparaît donc derrière l’expression de «fait de juger la grandeur de l’œuvre». Viollet-le-Duc utilise le terme et il y consacre un article de son Dictionnaire raisonné de l’architecture , mais il le confond avec la notion de proportion qui, de ce fait, est peut-être encore moins claire chez lui que chez Vitruve: «Admettons même qu’il tienne à donner à cette façade de grandes proportions, ou, pour mieux dire, une échelle supérieure à l’échelle commune [...]. Les Grecs ont eu assurément un module, ils ne semblent pas avoir eu d’échelle.» Il en va de même chez A. Choisy: «Parmi les édifices des Grecs, les seuls qui éveillent l’impression de la grandeur matérielle sont ceux de l’âge archaïque. Et cela tient, croyons-nous, à la lourdeur même de leurs proportions.» On voit que si la notion d’échelle fait son apparition au XIXe siècle, les deux notions de proportion et d’échelle sont loin d’être séparées et la grandeur ou la lourdeur des proportions dénoncent une utilisation métaphorique de la notion de proportion qui perd ainsi la précision mathématique qu’elle avait dans la définition d’Euclide.
La notion d’échelle joue une importance accrue dans Le Modulor de Le Corbusier, publié en 1950; et, en 1965, un ouvrage de Heath Licklider, Architectural Scale , est consacré au sujet.
Le changement d’échelle
Le synchronisme relatif entre la révolution industrielle et l’apparition du terme échelle dans un nouveau sens (le terme d’échelle en architecture ne joue dans l’Encyclopédie de Diderot que le rôle d’instrument de représentation graphique qui est le sien en cartographie) laisse peu de doutes sur l’interaction des deux phénomènes. L’examen théorique du Modulor révèle la présence, derrière le tempérament artistique de Le Corbusier, des deux liaisons fondamentales qui relient architecture et industrialisation.
a ) «Le besoin d’une nouvelle mesure est rendu impératif du fait que les grandes vitesses ont transformé les rapports des hommes et des peuples [...]. Il en résulte ceci: tout devient, tout est devenu solidaire.» Cela préfigure le nouvel espace dont Mac Luhan parlera ultérieurement mais qui est déjà présente dans cette phrase de Le Corbusier: «Les mesures qui servent à confectionner l’espace peuvent-elles demeurer locales?» où se trouve posé, sans que Le Corbusier lui-même se le soit explicité, le passage de la proportion à l’échelle , c’est-à-dire d’un système de dimensionnement clos à un dimensionnement relatif à une référence externe.
b ) «La grande industrie doit s’occuper du bâtiment et établir en série les éléments de la maison [...]. En pays d’U.S.A., voué à la série, j’aurais aimé apporter l’illimitée variété telle que semble l’assurer notre règle harmonique.»
Dans les deux cas Le Corbusier cherche une mesure qui apporterait l’«illimitée variété». Dans ces dialectiques du un et du multiple d’une part et du fermé et de l’ouvert d’autre part, le problème posé est le même, celui d’un urbanisme ouvert et celui d’une industrialisation ouverte.
Nous avons fait ici l’hypothèse d’une spécificité de la pensée architecturale qu’il serait possible de faire émerger des écrits pseudo-théoriques des architectes et de constituer en théorie scientifique unitaire et ouverte; cette attitude est différente de celle de Panofsky, pour qui l’architecture gothique n’est que la projection dans l’espace de la structure de la pensée scolastique, et de celle d’Henri Lefebvre pour qui l’urbanisme n’est que la projection de la société sur le sol. Dans les deux cas, ce qui est projeté préexiste à la projection: on ignore l’échelle qui est la règle suivant laquelle s’effectue la projection et en quoi réside justement la spécificité architecturale. Même à Viollet-le-Duc, il arrive de considérer l’architecture comme une suiveuse : «Si l’architecture est arrivée à un état de crise fort pénible et dangereux, c’est qu’on n’a pas assez songé à lui faire suivre le mouvement intellectuel et matériel de notre temps.» Peut-on faire l’hypothèse qu’il puisse exister une science de l’architecture qui serait science du projet dans l’espace réel, maillon manquant à la connaissance scientifique? Un premier essai consisterait à appliquer à l’architecture le processus du matérialisme. Mais si la pensée architecturale logique est plus qu’une suiveuse et réfléchit sa spécificité, il n’est pas impossible qu’elle enrichisse de sa problématique les courants actuels de pensée.
Depuis la «sphère des sphères» de Hegel, il n’est pas certain que l’espace réel ait été délivré de sa gangue métaphorique si l’on considère ce que certains courants matérialistes expriment à propos de l’espace: le «renversement» de la dialectique hégélienne de Marx, la «coupure» bachelardienne, ou encore le «déplacement d’espace des problèmes» d’Althusser. Ces pensées éminemment métaphoriques semblent faire bien peu état de la réalité de l’espace (ce qui est explicite chez Bachelard). S’il en était ainsi, une science du projet dans l’espace reliée aux autres savoirs pourrait éclairer grandement le rapport de la nouvelle échelle à un nouvel humanisme.
proportion [ prɔpɔrsjɔ̃ ] n. f.
• 1265; lat. proportio
1 ♦ Rapport de grandeur entre les parties d'une chose, entre une des parties et le tout, défini par référence à un idéal esthétique; plur. Combinaison des différents rapports; dimensions relatives des parties et du tout. « Juger de la beauté, c'est juger de l'ordre, de la proportion et de la justesse » (Bossuet). Échelle de proportion. Proportions harmoniques. Proportion de la hauteur et de la largeur, de la hauteur à la largeur, entre la hauteur et la largeur d'une façade. Juste, exacte proportion, proportion idéale, dans un style. ⇒ équilibre, harmonie. Règles, canon de proportions, divine proportion (cf. Nombre d'or). — Proportions du corps, des parties du corps, des traits du visage. Manque de proportion entre les jambes et le buste. « Telle proportion entre la grandeur de la tête et la grandeur de l'ensemble fait le corps florentin ou romain » (Taine). Élégance des proportions.
♢ Spécialt Proportion harmonieuse, correcte. La proportion des parties.
♢ Absolt et vieilli Beauté, harmonie des proportions, des dimensions relatives des parties et du tout. « La proportion produit l'idée de force et de solidité » (Diderot).
2 ♦ Sc. Rapport entre les différentes dimensions (d'une figure, d'un objet). L'homothétie conserve les proportions.
♢ (XIVe) Math. Égalité de deux rapports. Dans la proportion a/b = c/d, le produit des extrêmes (ad) est égal à celui des moyens (bc). Termes d'une proportion. — Géom. Compas de proportion.
♢ Chim. Loi des proportions définies (loi de Proust). Loi des proportions multiples.
3 ♦ Rapport quantitatif (entre deux ou plusieurs choses). Une proportion égale de réussites et d'échecs. Proportion de décès normale, élevée, faible (par rapport à la population). ⇒ pourcentage, taux. Dans, selon une proportion, la proportion de 10%, de cent contre un. Dans la même proportion (que...). Dans la proportion, l'exacte proportion où... ⇒ mesure. Accorder qqch. selon une proportion équitable, une juste proportion (⇒ proportionnellement) . En proportion insuffisante. Proportion d'or dans un alliage. ⇒ titre. Proportion de farine entrant dans la composition d'un gâteau.
4 ♦ Fig. et vieilli Relation que l'on établit entre deux choses que l'on compare. ⇒ analogie, correspondance. « Quelle proportion, à la vérité, de ce qui se mesure, quelque grand qu'il puisse être, avec ce qui ne se mesure pas ? » (La Bruyère). « Il faut quelque proportion dans une alliance » (Balzac).
5 ♦ À PROPORTION DE... : suivant l'importance, la grandeur relative de. ⇒ proportionnellement. Chose qui augmente à proportion de, en raison directe de. — À PROPORTION QUE... : à mesure que; dans la mesure où. « Nous ne souffrons qu'à proportion que le vice, qui nous est naturel, résiste à la grâce surnaturelle » (Pascal). — Loc. adv. À PROPORTION : suivant la même proportion.
♢ EN PROPORTION DE. ⇒ selon, 2. suivant (cf. En raison de). « Les héroïnes raciniennes prennent corps, prennent vie en proportion de l'obstacle contre lequel leur passion se précipite » (F. Mauriac). Le travail était payé en proportion des risques. C'est peu de chose, en proportion du service qu'il vous avait rendu, en comparaison de. ⇒ relativement (à). — EN PROPORTION AVEC... — Loc. adv. EN PROPORTION : suivant la même proportion. « Il était fabuleusement gros, et grand en proportion » (R. Rolland).
♢ HORS DE PROPORTION, hors de toute proportion : sans commune mesure avec (généralement beaucoup trop grand). ⇒ disproportionné. « C'est une récompense hors de toute proportion » (Giraudoux). La punition est hors de proportion avec la faute. — SANS PROPORTION. Sa colère est sans proportion avec leur dispute. — Toute(s) proportion(s) gardée(s).
6 ♦ LES PROPORTIONS : dimensions (par référence implicite à une échelle, une mesure). « De grands poêles aux proportions monumentales » (Gautier). Ramener une nouvelle à ses proportions véritables (⇒ relativiser) . « Ces deux phases, Waterloo et Sainte-Hélène, réduites aux proportions bourgeoises, tout homme ruiné les traverse » (Hugo).
⊗ CONTR. Discordance, disproportion.
● proportion nom féminin (latin proportio) Rapport relatif de grandeur existant entre une quantité et une autre, entre un nombre et un autre pris comme référence : Une proportion de un volume de riz pour deux d'eau. Quelle proportion d'élèves réussissent leur bac ? Rapport satisfaisant entre deux choses : Il n'y a aucune proportion entre la peine et la faute. Architecture Chacun des rapports de grandeur, plus ou moins satisfaisants pour l'observateur, dans les parties d'un édifice, entre plusieurs parties ou entre l'ensemble et ces parties. Mathématiques Mot autrefois utilisé pour désigner « l'égalité de deux fractions ». (
 (b ≢ 0 ; d ≢ 0) était appelé une proportion, a et d étaient les extrêmes, et b et c les moyens.)
● proportion (difficultés)
nom féminin
(latin proportio)
Orthographe
On écrit au singulier à proportion, en proportion (de), hors de (toute) proportion, sans proportion avec. - On écrit au singulier ou au pluriel toute(s) proportion(s) gardée(s).
● proportion (expressions)
nom féminin
(latin proportio)
À proportion, en proportion de, en raison directe de quelque chose, selon son importance.
Hors de proportion, sans proportion avec, disproportionné, démesuré, sans commune mesure avec ce qui est.
Loi des proportions définies, loi qui affirme que les rapports des masses suivant lesquelles deux ou plusieurs éléments se combinent sont déterminés et non susceptibles de variations continues.
Loi des proportions multiples, loi selon laquelle, quand deux éléments forment plusieurs composés, les masses de l'un d'eux qui s'unissent, dans ces divers composés, à une même masse de l'autre forment entre elles des rapports à termes entiers et généralement simples.
● proportion (synonymes)
nom féminin
(latin proportio)
Rapport satisfaisant entre deux choses
(b ≢ 0 ; d ≢ 0) était appelé une proportion, a et d étaient les extrêmes, et b et c les moyens.)
● proportion (difficultés)
nom féminin
(latin proportio)
Orthographe
On écrit au singulier à proportion, en proportion (de), hors de (toute) proportion, sans proportion avec. - On écrit au singulier ou au pluriel toute(s) proportion(s) gardée(s).
● proportion (expressions)
nom féminin
(latin proportio)
À proportion, en proportion de, en raison directe de quelque chose, selon son importance.
Hors de proportion, sans proportion avec, disproportionné, démesuré, sans commune mesure avec ce qui est.
Loi des proportions définies, loi qui affirme que les rapports des masses suivant lesquelles deux ou plusieurs éléments se combinent sont déterminés et non susceptibles de variations continues.
Loi des proportions multiples, loi selon laquelle, quand deux éléments forment plusieurs composés, les masses de l'un d'eux qui s'unissent, dans ces divers composés, à une même masse de l'autre forment entre elles des rapports à termes entiers et généralement simples.
● proportion (synonymes)
nom féminin
(latin proportio)
Rapport satisfaisant entre deux choses
Synonymes :
- équilibre
Contraires :
proportion
n. f.
d1./d Rapport de grandeur entre les différentes parties d'un tout.
— (Plur.) Ensemble des dimensions qui caractérisent un tout, considérées les unes par rapport aux autres. Les proportions des pyramides de Gizeh.
d2./d Par ext. (Souvent au Plur.) Dimensions.
— Fig. Ramener les faits à leurs justes proportions.
d3./d Rapport constant entre deux ou plusieurs grandeurs.
d4./d Rapport quantitatif, pourcentage.
— Loc. adv. à proportion: proportionnellement.
— Loc. adv. En proportion: dans un rapport constant. Syn. proportionnellement.
— Toutes proportions gardées: en tenant compte de la valeur relative, de la différence entre.
d5./d Quantité relative (lorsqu'il y a plusieurs éléments).
⇒PROPORTION, subst. fém.
A. —1. Rapport de grandeur entre les parties d'une chose, entre l'une d'elles et le tout; au plur., combinaison des différents rapports, des dimensions relatives entre les parties et le tout. À lui seul il est grand comme une nation. D'ordinaire, tout est dans la proportion, Et le petit est grand près du moindre, et l'arbuste, Si vous le comparez au brin d'herbe, est robuste (HUGO, Légende, t.3, 1877, p.388).
2. Équilibre harmonieux et respectant les normes de l'idéal, de l'esthétique. Proportions des parties, être en proportion (avec). La grâce [d'une porte] vient des proportions exactes entre les stylobates, les plinthes, les corniches et les ornements (BALZAC, C. Birotteau, 1837, p.198). La composition de ce charme, dans lequel la plus grande simplicité et la plus exquise «distinction» s'unissaient en proportion admirable (VALÉRY, Variété V, 1944, p.174):
• 1. ... j'entends par mesure le sens des proportions. Avoir de la mesure, c'est éviter le sublime ou l'horrible perpétuels, c'est se ménager la possibilité de crescendos allant jusqu'à l'exaltation et de diminuendos se dégradant jusqu'au silence.
RIVIÈRE, Corresp. [avec Alain-Fournier], 1906, p.85.
— Au plur. [En parlant du corps hum.] Dimensions respectant un canon esthétique ou un effet d'ensemble. Les bras étaient resserrés comme des momies; mais dans le doux pays de la Grèce, elles figurèrent l'homme et la femme dans toute la beauté des proportions: on crut voir respirer Vénus et marcher Apollon (BERN. DE ST-P., Harm. nat., 1814, p.337). Des enfants (un en particulier, protégé de Marc, d'une douzaine d'années, d'une surprenante robustesse, d'admirables proportions (...)) (GIDE, Retour Tchad, 1928, p.921).
SYNT. Proportion (+ de... et de..., de... à..., entre... et...); proportion de la hauteur et de la largeur, de la longueur à la largeur, entre la longueur et la profondeur (d'une façade, d'un édifice); exacte, juste proportion; proportion idéale; unité de proportion (synon. module); canon, règles de proportions; proportions harmonieuses du corps; des parties du corps; équilibre, harmonie des proportions.
B. —1. Rapport constant entre deux ou plusieurs grandeurs. Proportion des nombres. L'équation de proportion peut avoir (...) un nombre quelconque de termes (Arts et litt., 1935, p.28-5).
2. Spécialement
a) CHIMIE
♦Proportion(s) (chimique(s)). Rapport(s) des masses ou des volumes suivant lesquels se combinent les corps simples ou composés:
• 2. Revenons (...) au problème des proportions chimiques. Si des volumes égaux de gaz ou de vapeur renferment le même nombre de molécules et que, par conséquent, les poids relatifs de ces molécules sont proportionnels aux densités, il y a là un moyen d'établir d'une manière directe les poids atomiques de divers éléments.
Hist. gén. sc., t.3, vol. 1, 1961, p.313.
♦Principe, loi des proportions définies. Principe selon lequel deux corps simples s'unissent pour former un corps composé, dans une combinaison chimique, suivant des quantités fixes invariables. Les affinités chimiques ne donnent lieu qu'à (...) des combinaisons en proportions définies (COURNOT, Fond. connaiss., 1851, p.190).
♦Principe, loi des proportions multiples. Principe selon lequel deux corps simples s'unissent pour former plusieurs corps composés différents suivant des rapports simples entre leurs masses. La chimie (...) établit des lois générales, lois des équivalents définis et des proportions multiples, qui permettent d'étendre le calcul à toute la variété des combinaisons (BLONDEL, Action, 1893, p.66).
b) MATH. Rapport de quantités entre elles; en partic., égalité de deux ou plusieurs rapports, par différence ou par quotient. Proportion algébrique; termes, antécédents, conséquents, extrêmes, moyens d'une proportion. V. extrême II B 2 b ex. de Hadamard:
• 3. J'appris par coeur les tables de logarithmes: (...) un nombre étant donné dans la proportion géométrique, je trouvais de mémoire son exposant dans la proportion arithmétique, et vice versa.
CHATEAUBR., Mém., t.1, 1848, p.68.
♦Proportion continue. V. continu I A 2.
♦Proportion harmonique. V. harmonique D.
♦Règle de proportion. Synon. vx de règle de trois.
c) GÉOM. Compas de proportion.
C. —1. Rapport quantitatif entre deux ou plusieurs choses comparables. Proportion heureuse entre deux choses; proportion égale de réussites et d'échecs; proportion de 10 %, de cent contre un, de qqc. à qqc. Les cailles de la belle Aurore. Proportions pour six personnes. Choisissez six grosses cailles (...) assaisonnez l'intérieur d'un grain de sel et d'un filet de madère (Gdes heures cuis. fr., A. Escoffier, 1935, p.195). Les pays sous-développés sont en même temps des pays sous-éduqués, avec une proportion encore très élevée d'analphabètes (LESOURD, GÉRARD, Hist. écon., 1966, p.603).
— Proportion de x à, contre, pour, sur. L'Assemblée est une chambre introuvable; nous y sommes dans la proportion de 50 contre 700 (HUGO, Corresp., 1871, p.275). Les Allemands perdent du monde dans la proportion de trois à un. Si je perds cinquante mille hommes, ils en perdent cent cinquante mille (BARRÈS, Cahiers, t.11, 1916, p.159):
• 4. ... les chances qu'aurait Madame C... de retrouver l'exacte équivalence de M. V... étaient dans les proportions de 3,05 sur 975008. Autant dire qu'elle ne le retrouverait pas.
A. FRANCE, Île ping., 1908, p.365.
— Dans la même proportion (que); dans l'exacte proportion où; en faible, forte proportion; dans une faible proportion. Synon. de mesure. Le pouvoir créateur et la capacité de son intelligence ne se sont pas accrus dans les mêmes proportions qu'augmentait la masse des notions accumulées par les ancêtres et recueillies par l'héritage (GAULTIER, Bovarysme, 1902, p.43). Plus ce que vous dictez est grave, et intime, et plus il devrait vous être facile de le dicter dans la proportion même où vous n'avez pas d'intimité avec la personne qui l'enregistre (DU BOS, Journal, 1928, p.224):
• 5. Les luttes autour d'Ypres avaient montré une fois de plus la puissance que la défensive avait acquise par le développement des feux, l'emploi de la mitrailleuse en particulier. L'offensive n'avait pas encore grandi dans la même proportion.
FOCH, Mém., t.1, 1929, p.246.
2. Au fig., vieilli. Rapport de convenance entre deux choses. Synon. accord, analogie, convenance, correspondance, relation. Établir une proportion. Cela se borne à trop peu de chose pour déterminer un mariage sans fortune et sans proportion (LAMART., Corresp., 1835, p.152). Je ne puis comprendre ce don qui n'a pas proportion avec le crime (CLAUDEL, Choéphores, 1920, p.930).
3. Locutions
a) Loc. adv.
♦À proportion (vieilli), en proportion. Selon des mesures appropriées, en tenant compte du rapport des grandeurs; par comparaison. Synon. comparativement, proportionnellement, à l'avenant, en rapport. Il avait six pieds de haut, et il était gros à proportion, quoiqu'il n'eût que vingt-huit ans (TAINE, Notes Paris, 1867, p.98). Au cours des combats de 1940 (...) 500000 immeubles ont été complètement détruits, 1500000 gravement endommagés. En proportion, ce sont les usines qui ont principalement souffert (DE GAULLE, Mém. guerre, 1959, p.233).
♦Hors de proportion, sans proportion. Sans commune mesure, sans comparaison. Si je suis l'amant d'une femme du dernier acabit (...) où est l'unité de style dans les «scènes» que nous pouvons voir ensemble? Cette femme y est ce qu'elle est, et moi ce que je suis, qui sont sans proportion (MONTHERL., Notes théâtre, 1954, p.1075). V. hors II B 2 d ex. de Bernanos.
b) Loc. prép.
♦À proportion de (vieilli), en proportion (directe, inverse) de. En rapport avec. Dans l'âme (...) tout ce qui est menacé par le temps sécrète du mensonge pour ne pas mourir, et à proportion du danger de mort (S. WEIL, Pesanteur, 1943, p.64):
• 6. Tandis que le roi recevait moins d'argent, il en dépensait autant qu'auparavant; car les marchandises haussaient nominalement de prix en proportion de la diminution de la quantité d'argent contenue dans la livre.
SAY, Écon. pol., 1832, p.264.
♦En proportion avec. Proportionné à. Les moyens doivent être en proportion avec la fin, axiome très simple négligé de nos jours par beaucoup (MARITAIN, Primauté spirit., 1927, p.112).
♦Hors de proportion avec, sans proportion avec. Sans commune mesure avec. Dieu (...) nous console par l'espoir d'une récompense bien au delà et sans proportions avec ce que nous souffrons (RENAN, Souv. enf., 1883, p.143):
• 7. Si la véhémence de l'expression y paraît quelquefois hors de proportion avec la déviation, l'erreur ou la «faute» qu'ils prétendent flétrir, (...) il en faut incriminer le malaise des temps...
BRETON, Manif. Surréal., 2e Manif., préf., 1946, p.82.
c) Loc. conj. À proportion que (+ ind.). À mesure que, dans la mesure où. Le souvenir de nos amis grandit dans nos coeurs à proportion que nous nous éloignons d'eux par la distance (LAMART., Corresp., 1832, p.292). Le succès de l'expression sera difficile —et par là méritoire —à proportion que l'auteur est plus singulier (PAULHAN, Fleurs Tarbes, 1941, p.162).
D. —P. méton., au plur.
1. a) Dimensions considérées dans leur rapport respectant un canon esthétique ou quant à l'effet de l'ensemble. Belles, fortes, grandes, importantes, vastes proportions; proportions heureuses, exactes, justes, harmonieuses, grandioses. Les admirables proportions de la cathédrale, son élévation majestueuse au dessus de tout ce qui l'avoisine (MONTALEMBERT, Ste Élisabeth, 1836, p.343):
• 8. Il fallait tout deviner, imaginer de la majesté de l'édifice, de l'ampleur de ses proportions parce que tout se passait autour d'ampoules si voilées qu'on ne s'y habituait qu'après un certain temps.
CÉLINE, Voyage, 1932, p.246.
b) Grandeur ou quantité relative par rapport à une échelle de mesure. Proportions colossales, énormes, gigantesques, modestes. Le monstre leur paraissait de forme et de proportions assez humaines, à part la tête et la queue (A. FRANCE, Île ping., 1908, p.109).
2. Au fig. Importance matérielle ou morale de quelque chose. En voyant ses hésitations (...) j'eusse ramené à de justes proportions la jalousie que m'inspirait Albertine, parce que, la voyant ainsi les éprouver, j'aurais pris la mesure et découvert la limite de ses plaisirs (PROUST, Fugit., 1922, p.555).
SYNT. Mesurer les proportions d'un événement; ramener, réduire un fait à des proportions humaines, à ses vraies proportions; événement qui prend des proportions considérables, démesurées, effrayantes.
Prononc. et Orth.:[ ]. Att. ds Ac. dep. 1694. Étymol. et Hist. 1. a) Ca 1265 «rapport de grandeur entre deux choses» (BRUNET LATIN, Trésor, éd. F. J. Carmody, I, 3, 7, p.20); b) 1370-72 math. «égalité de deux rapports» (ORESME, Ethiques, éd. A. D. Menut, 285); av. 1615 proportion aritmetique (PASQUIER, Recherches, 804); 1680 proportion harmonique, géométrique (RICH.); c) 1835 chim. (BERZELIUS, Théorie des proportions chimiques ds BOUILLET 1859); 1875 loi des proportions définies (Lar. 19e); 2. a) 1636 à proportion de «selon, dans la mesure de» (MONET); b) 1649 à proportion que «par rapport à ce que, dans la mesure où» (S. DE CYRANO DE BERGERAC, L'Autre monde, éd. F. Lachèvre, 172); c) 1651 à proportion «suivant le même rapport de grandeur» (PASCAL, Imag. puissances trompeuses, 4, éd. Faugère ds LITTRÉ); 1679 id. «selon le rapport requis par l'harmonie de l'ensemble» (BOSSUET, Hist., III, 3, ibid.); d) 1770-83 proportion gardée (BUFFON, Oiseaux, t.8, ibid.); e) 1830 hors de toute proportion avec (BALZAC, Bal Sceaux, p.107); 3. 1690 subst. fém. plur. «dimensions par référence implicite à une échelle, une mesure» (FUR.); 1842 fig. (BALZAC, A. Savarus, p.5). Empr. au lat. proportio «rapport, analogie». Fréq. abs. littér.:2359. Fréq. rel. littér.:XIXes.: a) 5312, b) 2429; XXes.: a) 2268, b) 2833. Bbg. GOHIN 1903, p.338, 352. — Sculpt. 1978, p.687.
]. Att. ds Ac. dep. 1694. Étymol. et Hist. 1. a) Ca 1265 «rapport de grandeur entre deux choses» (BRUNET LATIN, Trésor, éd. F. J. Carmody, I, 3, 7, p.20); b) 1370-72 math. «égalité de deux rapports» (ORESME, Ethiques, éd. A. D. Menut, 285); av. 1615 proportion aritmetique (PASQUIER, Recherches, 804); 1680 proportion harmonique, géométrique (RICH.); c) 1835 chim. (BERZELIUS, Théorie des proportions chimiques ds BOUILLET 1859); 1875 loi des proportions définies (Lar. 19e); 2. a) 1636 à proportion de «selon, dans la mesure de» (MONET); b) 1649 à proportion que «par rapport à ce que, dans la mesure où» (S. DE CYRANO DE BERGERAC, L'Autre monde, éd. F. Lachèvre, 172); c) 1651 à proportion «suivant le même rapport de grandeur» (PASCAL, Imag. puissances trompeuses, 4, éd. Faugère ds LITTRÉ); 1679 id. «selon le rapport requis par l'harmonie de l'ensemble» (BOSSUET, Hist., III, 3, ibid.); d) 1770-83 proportion gardée (BUFFON, Oiseaux, t.8, ibid.); e) 1830 hors de toute proportion avec (BALZAC, Bal Sceaux, p.107); 3. 1690 subst. fém. plur. «dimensions par référence implicite à une échelle, une mesure» (FUR.); 1842 fig. (BALZAC, A. Savarus, p.5). Empr. au lat. proportio «rapport, analogie». Fréq. abs. littér.:2359. Fréq. rel. littér.:XIXes.: a) 5312, b) 2429; XXes.: a) 2268, b) 2833. Bbg. GOHIN 1903, p.338, 352. — Sculpt. 1978, p.687.
 ]. Att. ds Ac. dep. 1694. Étymol. et Hist. 1. a) Ca 1265 «rapport de grandeur entre deux choses» (BRUNET LATIN, Trésor, éd. F. J. Carmody, I, 3, 7, p.20); b) 1370-72 math. «égalité de deux rapports» (ORESME, Ethiques, éd. A. D. Menut, 285); av. 1615 proportion aritmetique (PASQUIER, Recherches, 804); 1680 proportion harmonique, géométrique (RICH.); c) 1835 chim. (BERZELIUS, Théorie des proportions chimiques ds BOUILLET 1859); 1875 loi des proportions définies (Lar. 19e); 2. a) 1636 à proportion de «selon, dans la mesure de» (MONET); b) 1649 à proportion que «par rapport à ce que, dans la mesure où» (S. DE CYRANO DE BERGERAC, L'Autre monde, éd. F. Lachèvre, 172); c) 1651 à proportion «suivant le même rapport de grandeur» (PASCAL, Imag. puissances trompeuses, 4, éd. Faugère ds LITTRÉ); 1679 id. «selon le rapport requis par l'harmonie de l'ensemble» (BOSSUET, Hist., III, 3, ibid.); d) 1770-83 proportion gardée (BUFFON, Oiseaux, t.8, ibid.); e) 1830 hors de toute proportion avec (BALZAC, Bal Sceaux, p.107); 3. 1690 subst. fém. plur. «dimensions par référence implicite à une échelle, une mesure» (FUR.); 1842 fig. (BALZAC, A. Savarus, p.5). Empr. au lat. proportio «rapport, analogie». Fréq. abs. littér.:2359. Fréq. rel. littér.:XIXes.: a) 5312, b) 2429; XXes.: a) 2268, b) 2833. Bbg. GOHIN 1903, p.338, 352. — Sculpt. 1978, p.687.
]. Att. ds Ac. dep. 1694. Étymol. et Hist. 1. a) Ca 1265 «rapport de grandeur entre deux choses» (BRUNET LATIN, Trésor, éd. F. J. Carmody, I, 3, 7, p.20); b) 1370-72 math. «égalité de deux rapports» (ORESME, Ethiques, éd. A. D. Menut, 285); av. 1615 proportion aritmetique (PASQUIER, Recherches, 804); 1680 proportion harmonique, géométrique (RICH.); c) 1835 chim. (BERZELIUS, Théorie des proportions chimiques ds BOUILLET 1859); 1875 loi des proportions définies (Lar. 19e); 2. a) 1636 à proportion de «selon, dans la mesure de» (MONET); b) 1649 à proportion que «par rapport à ce que, dans la mesure où» (S. DE CYRANO DE BERGERAC, L'Autre monde, éd. F. Lachèvre, 172); c) 1651 à proportion «suivant le même rapport de grandeur» (PASCAL, Imag. puissances trompeuses, 4, éd. Faugère ds LITTRÉ); 1679 id. «selon le rapport requis par l'harmonie de l'ensemble» (BOSSUET, Hist., III, 3, ibid.); d) 1770-83 proportion gardée (BUFFON, Oiseaux, t.8, ibid.); e) 1830 hors de toute proportion avec (BALZAC, Bal Sceaux, p.107); 3. 1690 subst. fém. plur. «dimensions par référence implicite à une échelle, une mesure» (FUR.); 1842 fig. (BALZAC, A. Savarus, p.5). Empr. au lat. proportio «rapport, analogie». Fréq. abs. littér.:2359. Fréq. rel. littér.:XIXes.: a) 5312, b) 2429; XXes.: a) 2268, b) 2833. Bbg. GOHIN 1903, p.338, 352. — Sculpt. 1978, p.687.
proportion [pʀɔpɔʀsjɔ̃] n. f.
ÉTYM. Fin XIIIe; 1230, porposcion; lat. proportio.
❖
———
1 Rapport de grandeur entre les parties d'une chose, entre une des parties et le tout défini par rapport à un idéal esthétique. Au plur. Combinaison des différents rapports; dimensions relatives des parties et du tout. — || « Juger de la beauté (cit. 5), c'est juger de l'ordre, de la proportion et de la justesse » (Bossuet). || Échelle (cit. 18) de proportion. || Dimensions absolues et proportions (→ Effet, cit. 9). || Proportions harmoniques ⇒ Beauté, harmonie. — En architecture (→ Architecte, cit. 1). || Proportion de la hauteur et de la largeur, de la hauteur à la largeur, entre la hauteur et la largeur d'une façade. || Juste, exacte proportion, proportion idéale, dans un style… ⇒ Équilibre, eurythmie (cit. 1), harmonie; et aussi symétrie. || L'ordre et les proportions des ornements d'un édifice (→ Assemblage, cit. 10). || Unité de mesure pour déterminer les proportions. ⇒ Module (cit. 1). || Règles de proportion (cf. Nombre d'or, section dorée). || Canon de proportions. — Proportions du corps des animaux (→ Membre, cit. 6), des parties du corps humain (→ Anthropologie, cit. 2. ⇒ Anthropométrie), des traits du visage (→ Face, cit. 7). || Équilibre (cit. 25) de ligne et équilibre de proportion. || Proportions harmonieuses, gracieuses… ⇒ Beauté (des formes), régularité (des traits). — Avoir de belles proportions (cf. Être bien fait, membré, proportionné). || Élégance des proportions. || Anomalie des proportions. ⇒ Difformité.
1 La notion de proportion est, aussi bien en logique qu'en esthétique, une des plus élémentaires, des plus importantes, et des plus difficiles à préciser; elle est tantôt confondue avec celle de rapport, qui lui est logiquement antérieure, tantôt (…) avec celle d'un ensemble, d'un enchaînement de rapports caractéristiques reliés par un module (…)
Matila M. Ghyka, in Encycl. franç., XVI, 28-4.
2 Dans les actes de la vie ordinaire, en évaluant des proportions, et en combinant des efforts, les hommes préparent ce qu'ils croient propre à rendre agréable leur passage sur la terre : c'est l'art.
É. de Senancour, De l'amour, p. 5.
3 (…) telle proportion entre la grandeur de la tête et la grandeur de l'ensemble fait le corps florentin ou romain.
Taine, Philosophie de l'art, t. II, p. 333.
♦ Spécialt. Proportion harmonieuse, correcte. || La proportion des parties. ⇒ Correspondance (cit. 1, Bossuet). || « Un monstre (…) dont le corps n'a aucune proportion avec (la) tête » (Fénelon, Télémaque). — Absolt, vx. || Beauté, harmonie des proportions, des dimensions relatives des parties et du tout.
4 (M. Crousaz) définit la proportion, l'unité assaisonnée de variété, de régularité et d'ordre dans chaque partie.
Diderot, Sur l'origine et la nature du beau, in Œ. esthétiques, p. 396.
5 La proportion produit l'idée de force et de solidité.
Diderot, Pensées détachées sur la peinture, in Œ. esthétiques, p. 786.
2 Rapport ou ensemble de rapports (dans le domaine des grandeurs). → Géométrie, cit. 8. || Les proportions des nombres (→ Éternel, cit. 10). || L'idée de grandeur implique celles de qualité, de proportion et de mesure (→ Mathématique, cit. 6).
♦ Chim. || Loi des proportions définies (loi de Proust), selon laquelle les rapports des masses suivant lesquelles des éléments se combinent sont déterminés, et ne sont pas susceptibles de variations continues. — Loi des proportions multiples (loi de Dalton), selon laquelle quand deux éléments forment plusieurs composés, les masses de chacun d'eux qui peuvent s'unir à une même masse de l'autre sont entre elles en rapports généralement simples, et toujours à termes entiers. ⇒ aussi Proportionnel.
♦ (V. 1370). Math. Égalité de deux rapports. || Termes d'une proportion. ⇒ Extrême, moyen. || Une proportion s'écrit 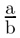 =
=  ou a : b = c : d (a est à b comme c à d). ⇒ Analogie. || Qui forme une proportion. ⇒ Proportionnel. — Proportion arithmétique, numérique. || Proportion harmonique. || Proportion géométrique. || Proportion continue, dont les moyens sont égaux entre eux. — Règle de proportion : règle de trois.
ou a : b = c : d (a est à b comme c à d). ⇒ Analogie. || Qui forme une proportion. ⇒ Proportionnel. — Proportion arithmétique, numérique. || Proportion harmonique. || Proportion géométrique. || Proportion continue, dont les moyens sont égaux entre eux. — Règle de proportion : règle de trois.
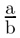 =
=  ou a : b = c : d (a est à b comme c à d). ⇒ Analogie. || Qui forme une proportion. ⇒ Proportionnel. — Proportion arithmétique, numérique. || Proportion harmonique. || Proportion géométrique. || Proportion continue, dont les moyens sont égaux entre eux. — Règle de proportion : règle de trois.
ou a : b = c : d (a est à b comme c à d). ⇒ Analogie. || Qui forme une proportion. ⇒ Proportionnel. — Proportion arithmétique, numérique. || Proportion harmonique. || Proportion géométrique. || Proportion continue, dont les moyens sont égaux entre eux. — Règle de proportion : règle de trois. ♦ Géom. || Compas de proportion.
3 (V. 1265). Cour. Rapport de nature quantitative (entre deux ou plusieurs choses). → Conscient, cit. 2. || Proportion entre… et…, de… et de… || Proportion heureuse… entre l'étendue des plaines et celle des montagnes (→ Côte, cit. 12). || Une proportion égale (cit. 7) de réussites et d'échecs, de valeurs et de déchets. || Proportion de décès normale (cit. 3), élevée, faible (par rapport à la population). ⇒ Pourcentage. || Les unités où la proportion des étrangers était la moins forte (→ 2. Fratricide, cit. 4). — Dans, selon une proportion (→ Charge, cit. 11), la proportion de 10%, de cent contre un, d'une souris à un éléphant (→ Gigantesque, cit. 3). || Dans la même proportion (que…). → Faire, cit. 270. || Dans des proportions démesurées, dérisoires, normales, moyennes. || Accorder qqch. selon une proportion équitable, une juste proportion (⇒ Proportionnellement). || Dans la proportion, l'exacte proportion où… ⇒ Mesure (→ Perception, cit. 6). — Dans une proportion faible, infime; en proportion insuffisante (⇒ Dose).
4 Fig., vieilli. Relation que l'on établit entre deux choses que l'on compare, rapport de convenance. ⇒ Accord, analogie, convenance (cit. 2, Bossuet), correspondance. || « Il doit y avoir une certaine proportion entre les actions et les desseins » (cit. 1, La Rochefoucauld). || Il n'y a pas de proportion entre ces choses-là (→ Bœuf, cit. 13). || Les proportions sont mieux gardées dans les états médiocres (→ Image, cit. 27, Rivarol). || Établir une proportion. ⇒ Proportionner.
6 Quelle proportion, à la vérité, de ce qui se mesure, quelque grand qu'il puisse être, avec ce qui ne se mesure pas ?
La Bruyère, les Caractères, XVI, 43.
7 Il faut quelque proportion dans une alliance. Mon fils aura un jour quatre-vingt mille livres de rente.
Balzac, Paméla Giraud, IV, 8.
5 ☑ (1636). Loc. littér. À proportion de… : suivant l'importance, la grandeur relative de… ⇒ Proportionnellement; avenant (à l'), raison (à). → aussi Sur un pied de… (→ Besoin, cit. 5; 2. bien, cit. 13). || Chose qui augmente (cit. 12) à proportion de…, en raison directe de… (→ aussi Force, cit. 62). || Le résultat n'était pas à proportion de l'effort. ⇒ Correspondre, répondre. — Partout on considère (cit. 12) les femmes à proportion de leur modestie. — ☑ À proportion que… (et l'indic.) : à mesure que (et, dans la mesure où…). → Discuter, cit. 8; habile, cit. 13. — ☑ Loc. adv. À proportion : suivant la même proportion (→ Hémisphère, cit. 4; multiplier, cit. 1).
8 Nous ne souffrons qu'à proportion que le vice, qui nous est naturel, résiste à la grâce surnaturelle (…)
Pascal, Pensées, VII, 498.
9 Peignant la vie, il (Rabelais) peindra l'action, et ces objets l'intéresseront à proportion qu'il y trouvera plus d'effort (…) plus d'action.
♦ ☑ (Mil. XVIIIe). Cour. En proportion de… ⇒ Égard (eu égard à), raison (en), selon, suivant (→ Articuler, cit. 3; corps, cit. 35; inégalité, cit. 4). || Le travail était payé en proportion des risques. ⇒ Prorata (au); → Fort, cit. 54. || C'est peu de chose, en proportion du service qu'il vous avait rendu. ⇒ Comparaison (en), relativement. — ☑ En proportion avec… (→ Luxe, cit. 2). — ☑ Loc. adv. En proportion : suivant la même proportion (→ Fourmillon, cit. 1; gros, cit. 5).
♦ ☑ Hors de proportion, hors de toute proportion : sans commune mesure avec… (→ Étale, cit. 3).
10 — L'avoine est bien chère, disait le maréchal des logis au maçon. — Elle n'est pas encore si renchérie que le plâtre, proportion gardée, reprit l'entrepreneur.
Balzac, la Vendetta, Pl., t. I, p. 910.
———
II (1690). || Les proportions : les dimensions (par référence implicite à une échelle, une mesure…). || Œuvre (cit. 21) de proportions colossales. || Les proportions commodes (cit. 2) d'une pièce. || De grands poêles (cit. 2) aux proportions monumentales. || Mesurer les proportions d'une catastrophe (⇒ Étendue), d'un événement (⇒ Intensité). || Ramener une nouvelle à ses proportions véritables.
11 Ces deux phases, Waterloo et Sainte-Hélène, réduites aux proportions bourgeoises, tout homme ruiné les traverse.
Hugo, les Travailleurs de la mer, III, I, I.
❖
CONTR. Discordance, disproportion.
Encyclopédie Universelle. 2012.