Akademik

LOGIQUE MATHÉMATIQUE

La logique au sens étroit du terme, c’est-à-dire la logique formelle par opposition à l’épistémologie ou à la théorie de la connaissance, se propose de donner une théorie de l’inférence formellement valide. Elle considère comme valide toute inférence telle qu’un individu sensé et suffisamment exercé se sente contraint de tenir sa conclusion pour vraie, du moment où il estime ses prémisses vraies. Une inférence est formellement valide si elle le demeure quand on fait varier arbitrairement, dans des limites fixées à l’avance, certains éléments de la phrase qui exprime l’inférence, c’est-à-dire quand on opère dans cette phrase certaines substitutions. «S’il y a du brouillard, la visibilité est mauvaise» est une inférence valide mais non formellement valide. Au contraire, «S’il y a du brouillard, la visibilité est mauvaise; or il y a du brouillard; donc la visibilité est mauvaise» est formellement valide. Le moyen le plus simple d’indiquer qu’une inférence est formellement valide consiste à désigner, en marquant leur place par des signes, les fragments de discours qui peuvent être arbitrairement remplacés sans que soit altérée la validité de l’inférence. La deuxième inférence citée s’écrira par exemple: «Si p , alors q ; or p ; donc q .» L’usage est de désigner les lettres ainsi employées du nom de variables , en précisant la nature du fragment de discours qu’elles remplacent. Dans l’exemple ci-dessus, p et q seront dites «variables de proposition». Dans la syllogistique fondée par Aristote, chez qui on trouve le premier usage systématique des variables, celles-ci représentent des termes comme «homme», «mortel», etc. Ainsi toute logique vraiment formelle est symbolique. La logique contemporaine se caractérise par la diversité des variables qu’elle considère (variables de proposition, d’individu, de prédicat, de relation, de fonction, etc.) plus que par son recours aux symboles.

L’usage des variables ne suffit pas à assurer à lui seul un développement satisfaisant à la logique. La langue usuelle est pleine d’ambiguïtés: «est» y exprime aussi bien l’appartenance que l’inclusion ou l’équivalence par définition; «ou» y est tantôt exclusif, tantôt non exclusif. Aussi remplace-t-on ces mots par des signes arbitrairement choisis, dits constantes , dont l’usage est fixé par des règles explicitement énoncées. On en arrive ainsi à constituer une langue complètement artificielle dont les éléments diffèrent suivant la nature des inférences qu’on entend étudier. Cependant, quel que soit le degré de complexité qu’on donne à une langue artificielle, celle-ci n’est pas une simple transposition de la langue usuelle, mais constitue toujours une reconstruction très schématique, où seuls sont retenus certains traits jugés importants. Le privilège dont jouissent les divers langages formels devenus aujourd’hui classiques tient essentiellement au fait qu’ils permettent d’exprimer, au prix de détours et d’artifices plus ou moins considérables suivant le cas, le plus grand nombre des énoncés aujourd’hui rencontrés en mathématiques.

Dans l’édification d’une logique, la construction d’une langue formelle n’est qu’une première étape. On peut poursuivre la tâche dans deux directions différentes:

– Pour pouvoir définir la déduction valide comme celle dont la conclusion a la valeur Vrai chaque fois que ses prémisses ont la valeur Vrai , il faut pouvoir déterminer la valeur de vérité prise par une expression complexe pour toute attribution de valeur aux lettres considérées dans cette expression comme variables de plein droit, c’est-à-dire qu’il faut disposer de règles d’évaluation. Le choix de celles-ci est libre, mais en pratique on adopte des règles qui conduisent à considérer comme valides les traductions formelles des raisonnements estimés légitimes dans la langue usuelle. De la sorte, on obtient une logique où on retrouve les lois usuellement acceptées et qui permet en outre de conclure dans des situations trop complexes pour que le simple «bon sens» conduise à un résultat assuré. Une telle façon de procéder est dite sémantique , quoiqu’elle ne fasse jamais appel au sens des expressions formelles, mais seulement au fait qu’elles peuvent désigner des êtres de nature donnée. La sémantique reste donc ici entièrement formelle. C’est elle qui sert de base à la théorie des modèles.

– On peut tout aussi bien considérer comme axiomes certaines expressions de la langue formelle et fixer des règles de déduction immédiate telles que toutes les expressions déductibles des axiomes au moyen des règles se traduisent en lois logiques quand on les exprime dans la langue usuelle. La logique se présente alors sous la même forme qu’une théorie mathématique axiomatisée et l’on dit qu’on a construit un système formel. L’étude de ces systèmes est l’objet de la théorie de la démonstration.

Malgré leurs différences, ces deux méthodes conduisent assez souvent aux mêmes résultats en ce sens que l’ensemble des expressions valides dans l’interprétation que l’on a en vue est identique à l’ensemble des expressions démontrables dans le système formel. Quand il en est ainsi, on peut adopter indifféremment l’une ou l’autre présentation. C’est le cas pour le calcul classique des propositions et le calcul classique des prédicats du premier ordre.

Dès lors que, par voie sémantique ou par construction d’un système formel, on est parvenu à préciser la notion de déduction et la notion apparentée de conséquence logique d’un ensemble d’expressions, on peut donner une présentation entièrement formelle des théories mathématiques. Pour cela il suffit d’enrichir la langue formelle de constantes mathématiques, de faire choix d’axiomes (qui, si l’on est dans la perspective des systèmes formels, viennent donc s’ajouter aux axiomes logiques) et d’étudier les conséquences de ces axiomes. On constate alors que les propriétés des théories formalisées dépendent dans une certaine mesure de la logique employée. Il arrive même qu’on puisse établir par voie logique des théorèmes mathématiques intéressants (cf. théorie des MODÈLES); mais, pour développer la logique jusqu’au point où elle peut rendre de tels services, il faut faire usage de moyens mathématiques non négligeables.

L’édification progressive de ce qu’on appelle aujourd’hui logique mathématique s’est accompagnée de débats mi-philosophiques, mi-techniques (rendus plus vifs par l’apparition de difficultés connues sous le nom de paradoxes ) dont les thèmes ont parfois orienté les travaux de toute une école. Nous ne pouvons en citer ici que quelques exemples:

– Peut-on donner une définition purement logique des notions mathématiques? Prolongeant l’œuvre de Gottlob Frege après en avoir redécouvert les principaux résultats, Bertrand Russell répond affirmativement, mais cela l’oblige en particulier à tenir pour purement logique un énoncé comme l’axiome de l’infini que l’on peut aussi bien estimer proprement mathématique.

– La pensée mathématique possède-t-elle une spécificité telle que toute reconstruction logique des mathématiques sera toujours inadéquate? L’intuitionnisme issu des travaux de L. E. J. Brouwer et de son école l’affirme et limite sa confiance à la partie des mathématiques qu’on peut construire par des procédés qu’il s’agit alors de préciser.

– En quel sens et dans quelle mesure la logique peut-elle espérer fonder véritablement les mathématiques? Du moment où l’on ne se contente pas de construire des déductions formelles à l’intérieur d’un système, mais où l’on entreprend d’étudier les propriétés de ce système (par exemple démontrer sa non-contradiction), il faut employer à titre d’outil une partie plus ou moins importante des mathématiques. Ne commet-on pas alors un cercle vicieux en faisant reposer les mathématiques sur une logique formalisée? L’étude de ce problème est l’un des objets de la théorie de la démonstration fondée par David Hilbert et développée par son école. Un théorème fondamental et riche de conséquences, dû à Kurt Gödel, a fixé définitivement, en 1931, la limite des résultats qu’on peut espérer obtenir en ces matières et a, par là même, profondément modifié l’aspect philosophique du problème.

Au total, l’opposition violente qui, à la fin du XIX^e siècle, dressait contre la logique mathématique les tenants de la logique traditionnelle a aujourd’hui à peu près disparu. La logique mathématique a acquis droit de cité chez les mathématiciens. Réciproquement, les possibilités d’analyse fine qu’elle apporte ont permis de mieux rendre justice aux grands précurseurs (comme Aristote, les stoïciens, Leibniz...) dont l’œuvre conserve, malgré les insuffisances que nous y découvrons, le mérite d’avoir été le premier pas vers une théorie rigoureuse de l’inférence formellement valide.

La logique mathématique est désormais trop vaste et trop diverse pour faire l’objet d’un article unique. À ses principales branches sont donc consacrés des articles spécialisés auxquels on se référera souvent ici: théorie axiomatique des ENSEMBLES, théorie des MODÈLES, RÉCURSIVITÉ, théorie de la DÉMONSTRATION, auxquels il faut ajouter INTUITIONNISME d’une part, ANALYSE NON STANDARD d’autre part.

Dans le présent article, on trouvera d’abord quelques indications historiques et méthodologiques; puis un exposé des concepts de base qui constitue à la fois, ce n’est pas fortuit, un tableau, très rapidement brossé, de l’ensemble de la discipline vers le milieu des années 1930, et le bagage nécessaire à la compréhension des articles spécialisés.

1. La genèse d’une nouvelle branche des mathématiques: quelques repères historiques

Des questions philosophiques dont est historiquement issue la logique mathématique, il n’est pas question de rendre compte ici (voir notamment histoire de la LOGIQUE, fondements des MATHÉMATIQUES, FORMALISME ET FORMALISATION, théorie de la DÉMONSTRATION, problèmes de HILBERT, INTUITIONNISME, B. BOLZANO, R. DEDEKIND, G. FREGE, B. RUSSELL). Nous nous proposons seulement de poser quelques jalons chronologiques sur un parcours qui, en un peu plus d’un siècle, a conduit la logique, en tant que discipline mathématique, du néant à la pleine existence.

Enfance: 1847-1908

La logique contemporaine naît au cours de la seconde moitié du XIX^e siècle au confluent de plusieurs courants de pensée.

Un premier pas est accompli par G. Boole et A. de Morgan, en 1847: ils développent le calcul propositionnel comme calcul booléen. C’est l’algébrisation de la logique , à laquelle contribuent également C. S. Peirce, E. Schröder, H. MacColl et d’autres.

Mais s’il fallait retenir une date unique de naissance, ce serait celle de la publication du Begriffsschrift de Gottlob Frege, 1879, qui marque le début de la formalisation de la logique et du formalisme comme philosophie programmatique des mathématiques. Dans cette œuvre géniale, mais largement méconnue jusqu’à Russell, apparaissent non seulement les ingrédients du calcul des prédicats (prédicats, variables et quantificateurs), mais aussi la «méthode logistique» dont l’essence tient dans la notion de système formel antérieur à toute interprétation. Peirce aboutit indépendamment à la notion de quantificateurs (le terme est de lui) vers 1885. De même, Russell rejoint, dans ses Principles of Mathematics de 1903, bon nombre des conclusions du Begriffsschrift .

Enfin la logique est appelée à un rôle décisif dans le vaste mouvement d’axiomatisation des mathématiques. L’analyse étant axiomatiquement ramenée à l’arithmétique, grâce à Weierstrass, Dedekind, Méray, Cantor, Bolzano, deux grandes questions se posent: que sont les entiers naturels? que sont les ensembles d’entiers – et donc, que sont les ensembles? La théorie cantorienne s’élabore entre 1873 et 1895 environ. Avant Cantor, Bolzano, précurseur génial mais dont l’œuvre sera occultée, dans une grande mesure, pendant un siècle (ses Paradoxes sur l’infini paraissent en 1851, trois ans après sa mort), et à la même époque Dedekind (Was sind und was sollen die Zahlen , 1888) et Frege (Grundlagen der Arithmetik , 1884 et Grundgesetze der Arithmetik , 1893-1903) développent une théorie logique des nombres finis et transfinis. G. Peano et son école contribuent au mouvement d’axiomatisation en créant des notations commodes, qui supplanteront celles de Frege, en élaborant des systèmes logistiques et des axiomatiques (notamment pour l’ensemble des entiers naturels), et en présentant les mathématiques de l’époque sous une forme axiomatisée systématique (le Formulaire de mathématiques , qui comprend une introduction suivie de cinq volumes, paraît entre 1894 et 1908). Enfin, Hilbert mène à bien l’axiomatisation complète de la géométrie euclidienne dans ses Grundlagen der Geometrie de 1899.

Ainsi peuvent s’énumérer les principaux acquis de cette première période. Une crise profonde ne tarde pas à les remettre en cause, obligeant les mathématiciens, pour la troisième fois dans l’histoire, à s’interroger sur les fondements même de leur savoir. Au V^e siècle avant J.-C. ce fut la crise des irrationnels; au début du XIX^e siècle, la crise des infinitésimaux; en ce début du XX^e siècle, ce sont les apories logiques et ensemblistes. Comme toute crise, la dernière a ses prodromes. Elle ne se déclenche cependant qu’au tournant du siècle, avec d’une part la découverte des paradoxes de Cantor (en 1899), Russell (en 1901), Burali-Forti (en 1897 – mais Cantor y avait songé dès 1895), Richard (en 1905); et d’autre part la démonstration par Zermelo (en 1904) du fait que tout ensemble peut être bien ordonné.

Face à la crise, trois attitudes, trois projets qu’on ne fera qu’évoquer de la manière la plus superficielle: le projet logiciste d’une réduction des mathématiques à une logique cohérente et suffisamment développée; le projet formaliste d’une solution définitive à tous les problèmes de fondements par l’application des mathématiques à leur propre langage pris dans sa dimension formelle (ainsi peut se définir la métamathématique ); le projet intuitionniste d’une profonde réforme des mathématiques, considérées comme saisies d’égarement.

Le programme logiciste est esquissé dans les Principles of Mathematics de Russell en 1903. Le programme formaliste commence d’être élaboré par Hilbert dans ses communications aux congrès de Paris de 1900 (le deuxième des célèbres «problèmes» de Hilbert consiste à démontrer la cohérence de l’arithmétique) et de Heidelberg de 1904 (où il formule son «programme»). Quant au projet intuitionniste, annoncé dès les années 1870 par Kronecker (qui, à défaut de freiner la diffusion des méthodes de Weierstrass, s’opposera avec succès, pendant vingt ans, aux idées de Cantor), il trouve une nouvelle expression chez Poincaré et les grands analystes parisiens (Baire, Lebesgue, Borel). Ils opposeront, surtout à partir de 1905, aux conceptions ensemblistes abstraites toute une série d’objections qui, sans constituer une doctrine entièrement cohérente, définissent l’esprit de ce qu’on a appelé le semi-intuitionnisme . Mais le premier manifeste de l’intuitionnisme strict est constitué par la thèse de L. E. J. Brouwer, soutenue en 1907.

Adolescence: 1908-1931

Le logicisme est le premier des trois grands projets fondationnels à trouver son accomplissement. Les Principia mathematica de A. N. Whitehead et B. Russell, œuvre monumentale parue entre 1910 et 1913, présentent un système formel cohérent absorbant la théorie des ensembles, système appelé théorie des types, et établit, grosso modo, la réduction de l’essentiel des mathématiques de l’époque à cette théorie. Ainsi se trouve fondée la thèse logiciste, mais seulement en un sens restreint, car la théorie des types n’est pas généralement considérée comme purement logique. Et comme d’une part on ne songe plus guère aujourd’hui à défendre la thèse dans sa version forte, et que d’autre part les systèmes formels d’inspiration hilbertienne, distinguant la dimension ensembliste de la dimension logique, ont rapidement été préférés à la théorie des types, l’influence des Principia a cessé de se faire sentir, du moins de façon directe, en logique mathématique. Leur rôle historique, en revanche, a été absolument déterminant.

Le programme formaliste suscite, au cours de cette période, de très nombreux travaux. En 1908, Zermelo propose une première axiomatisation de la théorie des ensembles. Mais son système définit un univers ensembliste assez pauvre, privé notamment des objets construits par induction transfinie. Il sera amélioré, au cours des années 1920, par T. Skolem et A. Fraenkel.

Pour voir le jour, ce système, dit de Zermelo-Fraenkel (ZF) au détriment de son troisième auteur, nécessitait la notion de langage égalitaire du premier ordre. Ébauchée dès 1915 par Löwenheim, ce singulier mathématicien qui travaillait seul, loin des universités, cette notion est reprise par Skolem en 1919-1920, et exposée de manière complète en 1928 dans les Grundzüge der theoretische Logik de Hilbert et Ackermann; ce sera l’un des principaux acquis de cette période.

De son côté, J. von Neumann (1925) transformait le système de Zermelo en y adjoignant une distinction entre deux types d’objets, les ensembles, qui sont (relativement) «petits», et les classes propres qui sont (très) «grandes», et que l’on peut caractériser notamment par le fait qu’elles ne peuvent appartenir à rien, ni ensemble ni classe. Amélioré par Bernays et par Gödel, ce système, désigné par les initiales de ses auteurs, NBG, est essentiellement équivalent à ZF, lequel est le système couramment utilisé aujourd’hui.

Revenons brièvement sur le calcul des prédicats, pour signaler certains retards qui semblent avoir affecté les premiers stades de son développement. On s’est souvent étonné du fait qu’au cours des années 1920, ni le théorème de complétude ni le théorème de compacité n’aient été formulés, alors qu’ils étaient à la portée d’un Skolem, par exemple, dès 1923. L’explication est sans doute que Skolem se désintéressait de la syntaxe, au profit d’un point de vue purement «modèle théorique» avant la lettre. Inversement, Herbrand, qui connaissait pourtant les travaux de Skolem, ne se fiait précisément qu’à la syntaxe.

Ce fut Gödel qui, dans sa thèse de 1930, démontra la complétude et la compacité du calcul des prédicats. L’année suivante, il publiait ses fameux théorèmes d’incomplétude (formulés, soit dit en passant, dans le cadre formel des Principia Mathematica ), résolvant ainsi ou plutôt prouvant l’impossibilité de résoudre le premier problème de Hilbert.

Il ouvrait ainsi deux voies. D’une part, en réfutant les thèses formalistes maximales de Hilbert, il obligeait la métamathématique à redéfinir ses objectifs et à élargir son champ conceptuel: la théorie de la démonstration, partant des travaux de Gentzen et de Herbrand, allait prendre son essor. D’autre part, Gödel posait la première pierre de la théorie des fonctions récursives.

À la même époque, Tarski créait la «sémantique scientifique». (Son article célèbre, «Le Concept de vérité dans les langages formalisés», quoique publié seulement en 1933, et traduit en allemand en 1935, est écrit dès 1931). Ce qu’il apportait à la logique, ce n’est pas la notion d’interprétation d’un langage formel dans un domaine d’objets, notion parfaitement claire, du moins dans chaque situation particulière, depuis le XIX^e siècle, mais un traitement mathématique de la question dans sa pleine généralité, comprenant une définition récurrente de la valeur d’une formule dans une structure quelconque en termes des valeurs de ses sous-formules. Il préparait ainsi le terrain à un débat philosophique, toujours actuel, sur le concept de vérité en général, mais aussi à la théorie des modèles.

Jeunesse: 1931-1963

S’ouvre alors pour la logique mathématique, désormais constituée en discipline scientifique, une période d’approfondissement et d’expansion. La publication, en 1934 et 1939, des deux volumes des Grundlagen der Mathematik de Hilbert et Bernays consacre, en y contribuant, la consolidation de la logique. Son développement conduit à une division en branches qui reste actuelle, même si certaines frontières ont perdu de leur netteté. Un historique détaillé ne pourrait d’ailleurs que reprendre les articles spécialisés, lesquels ne sauraient être exhaustifs même pour la période en question.

Contentons-nous de marquer, par quelques dates, le développement des principales recherches.

En théorie des ensembles, les deux dates clés sont 1938, quand Gödel démontre la cohérence relative de l’axiome du choix et de l’hypothèse généralisée du continu, et 1962, quand Paul Cohen établit la cohérence relative des négations, et par suite l’indépendance des deux énoncés. Le travail de Cohen relancera, au cours de la décennie suivante, une branche relativement peu active durant les deux précédentes.

La théorie des fonctions récursives prend son essor à partir de 1936 avec les travaux de Church, Kleene, Markov, Post et Turing. La récursivité classique se développe rapidement, et la résolution, en 1956, du problème de Post par A. Muchnik et R. Friedberg, qui inventent indépendamment la méthode de priorité, ouvre l’ère des généralisations. D’autre part, grâce à Turing en particulier, la notion de théorie axiomatisable se précise, et les grands résultats d’indécidabilité peuvent s’exprimer (Church, Rosser, Tarski...).

La théorie de la démonstration se développe en liaison avec l’intuitionnisme. G. Gentzen invente le calcul des séquents, tant classique qu’intuitionniste (1935), et donne la première démonstration de cohérence de l’arithmétique (1936). Après la Seconde Guerre mondiale, Gödel, G. Kreisel, K. Schütte donnent à la théorie une impulsion nouvelle.

L’intuitionnisme proprement dit suscite un immense intérêt. Un disciple de Brouwer, A. Heyting, en donne dès 1930 une première formalisation qui, sans être considérée comme pleinement satisfaisante par les intuitionnistes, permet du moins aux autres logiciens de se faire une opinion un tant soit peu précise, et d’établir des comparaisons avec les systèmes classiques. Un vaste mouvement rayonne à partir d’Amsterdam vers tous les centres de logique de l’époque. De nombreux logiciens non (exclusivement) intuitionnistes apportent leur contribution; parmi les plus connus, S. C. Kleene, dont l’apport est considérable, mais aussi Gödel qui dès 1931-1932 montre notamment que le calcul des propositions classique s’interprète dans le calcul intuitionniste. D’autres écoles constructivistes se développent parallèlement, la plus importante étant l’école soviétique: après les travaux strictement intuitionnistes de A. Kolmogorov (1925, 1932) et V. Glivenko (1929), c’est surtout le constructivisme de A. A. Markov qui va durablement marquer les mathématiques soviétiques.

Enfin, la théorie des modèles se constitue vers 1950 à partir des travaux de A. Tarski, L. Henkin, A. Robinson et A. Mal’cev. Les principales méthodes de construction des modèles s’élaborent au cours de la décennie, et 1962 est marquée par la résolution de la conjecture de face="EU Caron" ゲo ご par M. Morley, travail qui donnera lieu à partir de 1970 à d’étonnants développements.

Le congrès international de Berkeley, en 1963, consacré à la théorie des modèles, et dédié à la mémoire de Skolem qui vient de disparaître, confirme le succès de la dernière-née des spécialités logiques. Mais on y entend aussi P. Cohen et R. Solovay parler du forcing, A. Robinson d’analyse non standard (dont l’idée lui est venue en 1960), H. J. Keisler, R. Montague et d’autres de diverses logiques d’ordre supérieur, S. Kripke d’une sémantique des logiques modales, J. R. Shoenfield de degrés d’insolvabilité... Une nouvelle époque s’annonce.

Maturité: 1963-...

L’attribution à Paul Cohen de la médaille Fields en 1964 symbolise la profonde transformation, interne mais aussi et peut-être surtout externe, que subit la logique en l’espace de quelques années. À la fin des années 1950, la logique occupait au sein des mathématiques une place modeste. Encore marquée par ses origines philosophiques, qui n’étaient pas loin de constituer, aux yeux de nombreux mathématiciens, une tare, elle restait isolée, n’ayant pour voisins que quelques philosophes et quelques informaticiens enclins à la spéculation. Rares étaient les centres mathématiques où la logique était présente, rares les publications où elle apparaissait, rares les manuels où l’étudiant curieux pouvait compléter sa formation. Malgré la profondeur et la difficulté des résultats acquis jusque-là, la logique, dotée d’un nombre restreint de méthodes, était souvent vue comme une recherche «formaliste», voire précieuse (peut-être en raison de l’accent mis à l’origine sur les aspects syntaxiques), sans parenté réelle avec les «vraies» mathématiques, hérissées de calculs, gardiennes vénérables des «grands problèmes».

La floraison d’idées et de techniques nouvelles qui ébranle et renouvelle la logique modifie aussi profondément son «image» et son rôle.

Le forcing, qui compte parmi les quelques grandes idées mathématiques du siècle, ne permet pas seulement à Cohen d’apporter une réponse inattendue au premier problème de Hilbert. Il prend d’emblée une place centrale dans la théorie des ensembles, qui connaît alors, sous l’impulsion de R. Solovay, R. Jensen, D. Martin, J. Silver et d’autres un développement extraordinaire. L’analyse faite par Jensen de l’univers constructible de Gödel, qui lui permet notamment de montrer que l’hypothèse de Souslin n’y est pas vérifiée (1972), conduit S. Shelah au premier résultat d’indépendance en théorie des groupes (1975).

La notion de récursivité est étendue à des objets plus généraux que les relations et fonctions sur les entiers par Kleene, Kreisel et G. Sacks. Dans le domaine de l’indécidabilité, les efforts de M. Davis et de A. Robinson trouvent leur aboutissement en 1970 grâce à Y. Matijasevitch: le dixième problème de Hilbert, dernière des questions de logique restée ouverte, est résolu (par la négative).

En théorie des modèles, après les travaux fondamentaux de A. Ehrenfeucht, A. Mostowski, M. Morley, R. Vaught, H. J. Keisler, le concept central de théorie stable est défini par S. Shelah. Après les grands succès de J. Ax et S. Kochen et de Y. Ershov dans l’application de méthodes logiques à des questions très délicates d’algèbre (corps p -adiques, conjecture d’Artin), l’école d’A. Robinson élargit l’interface algèbre/logique. L’analyse non standard prend les dimensions d’une spécialité autonome.

La théorie de la démonstration, éperonnée par G. Kreisel notamment, s’approfondit et se diversifie. La formalisation de l’intuitionnisme s’achève, grâce à Kreisel et à A. S. Troelstra.

La décennie de 1970 voit l’aboutissement d’un grand nombre de travaux de première importance et l’ouverture de champs nouveaux. Il n’est pas sans valeur symbolique que le début des années 1970 soit marqué par la création d’un nouveau périodique, Annals of Mathematical Logic , et la fin par la publication du monumental Handbook of Mathematical Logic qui tente, sans y parvenir tout à fait, de donner en 1 200 pages, sans démonstrations autres qu’esquissées, un panorama de la discipline à l’usage du mathématicien non logicien.

Mis à part l’énorme accroissement quantitatif, comment caractériser l’évolution des années suivantes? En premier lieu, il est devenu difficile, sinon impossible, de distinguer méthodologiquement la logique de n’importe quelle autre branche des mathématiques: d’une part son développement obéit à une «logique» proprement mathématique, et non plus (exception faite, peut-être, de la théorie de la démonstration) à des motivations philosophiques; d’autre part, qu’on s’en réjouisse ou pas, elle a atteint un niveau de complexité et de spécialisation qui ne laisse guère à désirer; il n’est plus possible à un logicien de dominer la totalité de la discipline, et même au sein des quatre grandes branches, le chercheur est amené à se spécialiser. En ce sens, l’unité de la logique, ainsi ramenée à la condition ordinaire d’une juxtaposition de spécialités distinctes, peut sembler compromise. Mais, inversement, d’autres recherches ont mis au jour certains liens profonds entre des parties de la logique vues depuis l’origine comme disjointes. Ce double phénomène illustre d’ailleurs la dualité qui caractérise l’approfondissement en cours. La logique se développe désormais, d’une part, sur le plan déterminé par les problèmes posés au sein de chaque spécialité, dont la solution appelle la constitution de sous-spécialités, et tend, d’autre part, à dépasser sa propre fragmentation en découvrant de «bonnes» généralisations, celles qui mettent en évidence les idées-forces, souvent masquées, qui structurent le domaine. Cette opposition, qui se retrouve dans les principaux domaines mathématiques, témoigne précisément du degré de maturité auquel est parvenue la logique.

Le second grand changement intervenu à cette époque concerne les rapports que la logique entretient avec les autres disciplines mathématiques. Un fructueux commerce est établi avec l’algèbre, certes, mais aussi avec diverses parties de l’analyse, de la topologie, de la théorie des nombres, de la théorie des catégories. De plus, l’informatique théorique a repris à son compte de vastes fragments de logique, fournissant en échange la matière de nouvelles investigations. L’isolement brisé, les préventions tombent graduellement, et la logique occupe de plus en plus souvent, dans les universités, la place qu’elle a su mériter: celle d’une branche des mathématiques à part entière.

2. Les notions fondamentales: la logique du premier ordre

Langages formels

Tout langage L, qu’il soit naturel ou (plus ou moins) artificiel, donne à distinguer les objets suivants:

– un vocabulaire face=F9796 A, composé des «mots» de L;

– une collection face=F9796 de suites finies de mots qui sont les «phrases» (admissibles, «grammaticales») de L;

– une collection face=F9796 D de suites finies de phrases qui sont les «textes» (admissibles, «cohérents») de L.

Les règles de formation de face=F9796 constituent la morphologie de L, les règles de formation de face=F9796 D sa syntaxe . D’autre part, ce langage est utilisé pour décrire un domaine, une «réalité» donnée: les règles de correspondance entre les éléments de L (mots, lettres, phrases) et les aspects de la réalité (objets, faits, enchaînements de faits) constituent la sémantique de L.

Naturellement, la description, tant morphologique et syntaxique que sémantique, de L s’effectue à l’aide d’un langage considéré comme transparent: une distinction essentielle s’établit d’emblée entre ce langage de travail, appelé métalangage (ou métalangue ) et le langage étudié L, appelé aussi langage objet . Ce dernier est soit disjoint du métalangage (dictionnaire bilingue, cours de latin donné en français...), soit plongé dans le métalangage (dictionnaire «monolingue», cours de français donné en français...).

Cette deuxième situation est constitutive de la logique mathématique, dont la métalangue est le langage mathématique ordinaire, avec ce qu’il comporte de formalisation, de pratiques déductives et d’ontologie ensembliste «naïves» (au sens technique, c’est-à-dire non soumises à une axiomatisation). Les langages objets considérés sont d’une grande variété, mais constituent la formalisation d’autant de fragments du langage mathématique: leur syntaxe résulte d’une purification et d’une systématisation de ce langage, tandis que leur sémantique les rend aptes à décrire une certaine réalité mathématique (certains aspects de certaines familles de structures). Il existe même des langages permettant, en principe, de formaliser la totalité du discours mathématique: ce sont les langages ensemblistes (cf. infra : Les langages du premier ordre et théorie axiomatique des ENSEMBLES).

Un langage formel L est donné par:

– son alphabet ou ensemble de symboles , qui est un ensemble face=F9796 A (au sens mathématique) non vide;

– l’ensemble de ses formules , ou expressions bien formées , qui est un sous-ensemble face=F9796 de l’ensemble face=F9828 m face=F9796 A des suites finies de face=F9796 A;

– l’ensemble de ses preuves , ou démonstrations , ou dérivations , ou inférences , qui est un sous-ensemble face=F9796 D de l’ensemble face=F9828 m face=F9796 des suites finies de face=F9796 . (Pour s’aider d’une comparaison, on songera aux langues idéographiques plutôt qu’aux langues phonétiques; les éléments de face=F9796 A jouent le rôle des mots, non celui des lettres des langues naturelles.)

On appelle souvent système formel la donnée d’un alphabet face=F9796 A et des règles de formation de face=F9796 et de face=F9796 D. En pratique, les termes «système» et «langage» (formel) sont interchangeables. L’interprétation, ou plutôt les interprétations possibles d’un tel système sont déterminées par la sémantique de L, dont les règles précisent dans quelles conditions L permet de décrire une structure mathématique donnée: les éléments de face=F9796 A seront interprétés par des éléments de la structure, par des relations ou par des fonctions sur la structure, les éléments de face=F9796 par des assertions portant sur la structure, les éléments de face=F9796 D comme des suites de telles assertions.

La description des deux langages formels fondamentaux, à laquelle est consacré l’essentiel du présent chapitre, éclairera dans un instant ces notions quelque peu abstraites. Mais on peut déjà deviner que les langages formels donnent lieu à deux approches distinctes, quoique complémentaires, l’une privilégiant la syntaxe, l’autre la sémantique. Cette dichotomie explique d’une part sans doute certains retards dans le développement de la logique (voir au chapitre 1, Adolescence , l’exemple du théorème de complétude), d’autre part certaines bifurcations importantes au sein de la discipline. La logique tire néanmoins sa force, dans une large mesure, précisément de la convergence des deux approches. La possibilité d’une convergence dépend de la coïncidence plus ou moins grande entre les «faits» ou «vérités» syntaxiques que sont les formules démontrables dans le système formel, d’une part, et les faits ou vérités sémantiques que sont les formules vérifiées dans la ou les structures interprétatives, d’autre part. Quand la coïncidence est parfaite, on dit que le langage (ou le système) formel est complet . On conçoit l’importance, aux tout premiers stades de développement de la logique mathématique, des théorèmes de complétude et d’incomplétude, dont on trouvera plus loin les énoncés précis.

Calcul propositionnel

Le calcul propositionnel constitue un système formel rudimentaire, si pauvre qu’aucune théorie mathématique sérieuse ne peut y être formalisée. Il présente cependant un triple intérêt:

1. C’est le plus ancien système connu; si limité soit-il, il permet cependant le développement d’une logique élémentaire à laquelle toute la logique ou presque s’est longtemps ramenée.

2. Il constitue un noyau minimal commun à tous les systèmes (classiques) utilisés aujourd’hui, leur partie «triviale».

3. Méthodologiquement et pédagogiquement, il joue le rôle d’un «modèle réduit», d’une construction simplifiée qui se prête à l’élaboration et à l’assimilation de concepts et de méthodes applicables aux systèmes plus riches, donc plus complexes, utilisables en mathématiques.

On se donne un ensemble infini face=F9796 P dit ensemble des variables propositionnelles . Le calcul propositionnel construit sur face=F9796 P est le langage formel face=F9796 S constitué comme suit.

Morphologie

Le vocabulaire ou alphabet face=F9796 A se compose de face=F9796 P et de deux symboles n’appartenant pas à face=F9796 A appelés connecteurs : la négation , notée 囹 et l’implication , notée 轢.

Les règles de formation des formules, qui sont des suites finies de face=F9796 A, sont les suivantes:

I. Toute suite ayant pour unique terme une variable propositionnelle est une formule.

II. Si A est une formule, la formule dont le premier terme est 囹, suivi des termes de A (dans le même ordre), est une formule notée (face=F0019 囹A) (non A).

III. Si A et B sont deux formules, la formule obtenue en faisant suivredes termes de A puis des termes de B est une formule notée (AB) (A implique B).

IV. Toute formule est obtenue par itération des trois procédés ci-dessus.

On supprime les parenthèses quand il n’y a pas de risque de malentendu. Soulignons à ce propos que les objets considérés dans un langage formel appellent une triple distinction: ce sont des objets formels , c’est-à-dire des éléments d’un ensemble mathématique (très précisément celui des suites finies de face=F9796 A), qui sont désignés des multiples manières admises des mathématiciens, et interprétés par d’autres objets mathématiques. Il ne s’agit donc pas d’un couple tel que signe / sens ou signifiant / signifié, mais d’une triade objet / désignateur / valeur, ou si l’on veut objet / signe / sens.

Syntaxe

Les règles de formation des preuves, qui sont des suites finies de formules, sont les suivantes:

I. On appelle axiome toute formule ayant l’une des formes:

où A, B, C sont des formules quelconques; toute suite ayant pour unique élément un axiome est une preuve.

II. Si D est une preuve, A un axiome, la suite obtenue en faisant suivre les termes de D par A est une preuve.

III. Si D est une preuve ayant deux termes de la forme A et (AB), où A et B sont deux formules quelconques, la suite obtenue en faisant suivre les termes de D par B est une preuve; on dit que B a été obtenue ou inférée dans D par la règle de déduction ou d’inférence appelée modus ponens , ou règle de détachement (en abrégé MP), appliquée aux formules A et (AB).

IV. Toute formule est obtenue par itération des procédés ci-dessus.

Une formule F est dite prouvable , ou appelée un théorème (ou encore théorème formel – la terminologie est assez fluctuante), s’il existe une preuve dont elle est le dernier terme, preuve qui est dite preuve de F; on note vdash; face=F9796 S F, en omettant si possible l’indice face=F9796 S. On trouvera en encadré (cf. tableau), à titre d’exemple, une preuve dans face=F9796 S de la formule (FF), où F est une formule quelconque.

Enfin, soit un ensemble de formules et F une formule. Si F est prouvable dans le système formel obtenu en adjoignant à l’ensemble des axiomes de face=F9796 S, on dit que F est prouvable à partir de dans face=F9796 S, ou encore que F est une conséquence (formelle ) de dans face=F9796 S; on note 塞 face=F9796 S F, en omettant si possible l’indice face=F9796 S. Ainsi, la formule (FH) est conséquence de(FG), (GH) (cf. tableau).

Sémantique

L’interprétation du calcul propositionnel construit sur face=F9796 P comprend une partie fixe et une partie variable. Les variables et les formules prennent toujours leurs valeurs dans un ensemble face=F9796 B à deux éléments notés faux et vrai ou encore 0 et 1. Le connecteur 囹 est interprété par l’application 囹漣 : face=F9796 Bface=F9796 B telle que 囹漣(0) = 1 et 囹漣(1) = 0, ce qu’on exprime en général à l’aide d’une règle, dite table de vérité de la négation, donnant, pour une formule quelconque A, la valeur de vérité de A (c’est-à-dire l’élément de face=F9796 B qui interprète cette formule dans l’interprétation considérée) en fonction de celle de A:

Le connecteurest interprété par l’application 轢漣 : face=F9796 B 憐 face=F9796 Bface=F9796 B prenant la valeur 1 sur les couples (0, 0), (0, 1) et (1, 1), et la valeur 0 sur le couple (1, 0); la table de vérité de l’implication donne la valeur de vérité de (AB) en fonction des valeurs de vérité de A et B:

Cela fixé, toute application v de face=F9796 P dans face=F9796 B s’étend de manière unique en une application 率 de l’ensemble des formules dans face=F9796 B respectant les tables de vérité. Une telle application v : face=F9796 Pface=F9796 B s’appelle assignation , ou valuation , ou encore distribution de valeurs de vérité .

Une formule F prenant la valeur vrai (1) dans toute assignation est une tautologie du calcul propositionnel; on note |= F. Ainsi, soit p et q deux variables propositionnelles; la formule (pp ) est une tautologie, la formule (p(face=F0019 囹p )) est une antitautologie (elle prend la valeur 0 dans toute assignation, sa négation est une tautologie), la formule (pq ) est contingente (elle prend tantôt la valeur 0, tantôt la valeur 1).

Une assignation dans laquelle tout élément d’un ensemble de formules prend la valeur vrai est un modèle de . Une formule F vraie dans tout modèle de est une conséquence tautologique de ; on note |= F. Ainsi, on vérifie que pour toutes formules F, G, H la formule (FH) est conséquence tautologique de(FG), (GH). Deux formules prenant les mêmes valeurs dans toute assignation sont dites synonymes (ce qui équivaut à ce que chacune est conséquence tautologique de l’autre). Ainsi, les formules (FG) et ((face=F0019 囹G)(face=F0019 囹F)) sont synonymes.

Autres connecteurs, dialectes

Avant d’aborder la question centrale des rapports entre syntaxe et sémantique de face=F9796 S, il faut mentionner les nombreux enrichissements et variantes de ce système, qui constituent autant de dialectes d’un langage formel polymorphe mais essentiellement unique qui seul mérite d’être proprement appelé le calcul propositonnel.

En premier lieu, il est possible et en pratique souhaitable d’introduire d’autres connecteurs d’usage constant en mathématiques: la disjonction (inclusive), notée 鈴; la conjonction, notée 廬; la bi-implication, notée 兩. Morphologiquement, une notation telle que A 鈴 B est comprise (dans le contexte de face=F9796 S) comme désignant la formule (face=F0019 囹A)B; A 廬 B désigne 囹(A 轢(face=F0019 囹B)); A 兩 B désigne (AB) 廬 (BA), c’est-à-dire 囹((AB)囹(BA)). Ces «traductions» ne sont pas uniques: il n’est pas strictement équivalent de décréter que A 鈴 B abrège (face=F0019 囹A)B plutôt que (face=F0019 囹B)A; mais ces deux dernières formules sont équivalentes tant syntaxiquement que sémantiquement – chacune est conséquence formelle et tautologique de l’autre.

Ces nouveaux connecteurs donnent lieu à des théorèmes de syntaxe – la formule (A 鈴 B)A, par exemple, est prouvable – et de sémantique – les tables de vérité, par exemple, sont:

En deuxième lieu, le système face=F9796 S n’est nullement le seul possible, ni même le meilleur à tous points de vue. D’abord, la liste des axiomes et des règles d’inférence peut être modifiée de nombreuses façons. Certains systèmes sont plus élégants que d’autres, certains plus commodes. On peut rechercher des axiomes peu nombreux et indépendants, mais les preuves sont alors souvent longues et parfois difficiles à trouver. Inversement, les systèmes qui évitent cet inconvénient reposent sur une kyrielle d’axiomes donnant une peu «naturelle» image des «lois fondamentales de la pensée». Les systèmes dits de déduction naturelle ont précisément été élaborés (à partir des travaux de G. Gentzen par E. Beth, K. Schutte, J. Hintikka, D. Prawitz, R. Smullyan) pour réduire l’arbitraire de la formalisation et la rendre plus fidèle aux mécanismes logico-linguistiques «naturels» (c’est-à-dire familiers aux mathématiciens) – le prix à payer étant que les preuves ne sont plus des suites, mais des arbres finis (cf. théorie de la DÉMONSTRATION). Tous les systèmes existants sont cependant nécessairement équivalents – au sens où ce qui est prouvable dans l’un est prouvable dans chacun des autres – du seul fait que, pour mériter l’appellation de système formel pour le calcul propositionnel, ils doivent être complets (cf. infra ).

En troisième lieu, le partage entre connecteurs primitifs (ici 囹, 轢) et connecteurs dérivés (ici 鈴, 廬, 兩) n’a rien de canonique. On peut tout aussi bien partir de囹, 鈴參 (comme Hilbert et Ackermann), de囹, 廬參 (comme Rosser), voire囹, 鈴, 廬, 轢, 兩參 (comme Kleene), etc. La condition que doit remplir l’ensemble C des connecteurs primitifs est que leurs interprétations comme fonctions booléennes (prenant leurs arguments et leur valeur dans face=F9796 B) engendrent, par composition, toute fonction booléenne. Les plus puissants des connecteurs, à cet égard, sont la barre de Sheffer ou d’incompatibilité | – la formule A | B est fausse si et seulement si A et B sont vraies (A | B est donc synonyme de 囹(A 廬 B)), et la barre de Sheffer duale ou négation conjointe 醴 – la formule A 醴 B est vraie si et seulement si A et B sont fausses (A 醴 B est synonyme de 囹(A 鈴 B)). En effet, la seule barre de Sheffer suffit à engendrer tous les autres connecteurs (pour parler vite: il s’agit évidemment des fonctions booléennes correspondantes), et il en est de même de 醴. Naturellement, à chaque choix de connecteurs primitifs (assortis de leurs tables de vérité) correspondent diverses syntaxes adéquates.

En dernier lieu, le lecteur aura remarqué qu’indépendamment du choix des connecteurs et de la syntaxe, il y a à proprement parler autant de calculs propositionnels que d’ensembles face=F9796 P de variables propositionnelles. En pratique, seule la cardinalité de face=F9796 P peut intervenir de manière significative; on choisit face=F9796 P dénombrable en général, mais des ensembles non dénombrables interviennent dans certains cas. Les principales propriétés sont cependant insensibles à cette différence.

Complétude du calcul propositionnel

Un système formel pour le calcul propositionnel est complet si:

I. Toute formule prouvable dans le système est tautologique.

II. Toute formule tautologique est prouvable.

La première de ces propriétés répond à une exigence minimale, et s’établit facilement (on choisit pour axiomes des tautologies et on s’assure que l’ensemble des tautologies est clos pour les règles d’inférence). Elle a pour conséquence la cohérence de face=F9796 S: il n’existe pas de formule F telle que 塞 face=F9796 S F et 塞 face=F9796 S 囹F. La seconde propriété constitue le critère décisif – elle est moins facile à obtenir (quand on cherche un «bon» système), plus difficile à établir (une fois qu’on l’a trouvé).

Le système face=F9796 S, ainsi que les différents systèmes existants, sont complets. Il existe plusieurs démonstrations de ce résultat (la première, due à E. Post, date de 1921) – et les différences essentielles ne sont pas liées à la diversité des systèmes considérés (mis à part les systèmes à la Gentzen : cf. théorie de la DÉMONSTRATION). Nous donnerons, pour leur intérêt propre, quelques indications sur deux de ces démonstrations.

La première méthode repose sur les propriétés syntaxiques dites d’introduction et d’élimination des connecteurs. L’une des plus significatives est l’introduction de 轢, démontrée en 1930 par J. Herbrand: pour tout ensemble 鈴F 鈴G de formules, si 鈴F vdash;G, alors 塞 FG. Ce résultat, appelé aussi théorème de la déduction , constitue un pas vers la déduction (mathématique) naturelle: le mathématicien raisonne en général, dans le cadre d’une théorie fixée , à partir d’hypothèses admises (considérées comme vérifiées) F, pour conclure à G: ayant donc montré que 鈴F 塞 G, il peut énoncer le théorème: 塞 FG. L’élimination den’est autre que le modus ponens : face=F0019F, FG 塞 G. L’introduction de 囹 est la règle mieux connue sous le nom de reductio ad absurdum : si 鈴F 塞G et 鈴F 塞 囹G, alors 塞 囹F. La négation s’élimine de deux façons: F, face=F0019 囹F 塞 G (faible), face=F0019 囹(face=F0019 囹F) 塞 F (forte). Une fois établies ces règles, on peut oublier les axiomes et produire, de façon constructive, à partir d’une tautologie F, une preuve de F dans face=F9796 S (démonstration de L. Kalmar, 1934).

Une autre approche, développée par l’école polonaise, met en lumière la nature algébrique du problème, étroitement lié au théorème de représentation des algèbres de Boole dû à M. H. Stone (1936). En ordonnant l’ensemble des formules par la relation 諒 telle que F 諒 G si et seulement si 塞 face=F9796 S FG, et en le divisant par la relation d’équivalence 黎 telle que F 黎 G si et seulement si (F 諒 G et G 諒 F), on obtient une algèbre de Boole dont l’élément maximal est la classe d’équivalence des formules prouvables: c’est l’algèbre de Lindenbaum de face=F9796 S (A. Lindenbaum, A. Tarski vers 1935). La complétude découle alors immédiatement de l’existence d’un ultrafiltre contenant un élément non nul donné dans une algèbre de Boole. Cette démonstration, due à M. Rasiowa et R. Sikorski (1951), est essentiellement non constructive, puisqu’elle repose sur le lemme de Zorn. Mais elle est élégante, et s’étend au calcul des prédicats, pour lequel il n’existe précisément pas de solution constructive.

Complétude forte et compacité

Soit un ensemble de formules cohérent , c’est-à-dire tel qu’il n’existe pas de formule F telle que 塞 face=F9796 S F et 塞 face=F9796 S 囹F (la cohérence de face=F9796 S, définie plus haut, n’est donc autre que la cohérence de = 歷). Si est fini, par complétude possède un modèle – sans quoi la négation de la conjonction F des formules de serait tautologique, donc prouvable, et l’on aurait 塞 F et 塞 囹F. Quand est infini, la propriété subsiste: ainsi s’énonce la complétude forte de face=F9796 S. Mais la démonstration incorpore un phénomène nouveau, qui a son importance propre: c’est la compacité de face=F9796 S. Le théorème de compacité (dit aussi de finitude ), selon lequel un ensemble de formules de face=F9796 S a un modèle dès que chacun de ses sous-ensembles finis a un modèle, est une conséquence immédiate de la complétude forte et du caractère fini de la relation 塞 face=F9796 S F. Mais c’est aussi, sans détour syntaxique, une conséquence directe du théorème de Tychonoff (un produit de compacts est compact, cf. TOPOLOGIE). Tous ces résultats dépendent de l’axiome du choix (et lui sont même essentiellement équivalents).

Le théorème de complétude forte établit l’équivalence complète, du point de vue de la vérité, entre syntaxe et sémantique: les symboles 塞 et |= sont interchangeables.

Calcul des prédicats du premier ordre

Il est clair que le calcul propositionnel est radicalement insuffisant pour formaliser les mathématiques même les plus élémentaires. L’assertion «16 est pair et 4 est pair» n’a aucun intérêt. Avec «donc» au lieu de «et», elle n’a aucun sens, sauf à la comprendre comme instance de «x ² est pair donc x est pair», et de pouvoir considérer l’assertion: «pour tout x , si x ² est pair alors x est pair». (Cet exemple montre en passant que, contrairement à une opinion répandue, l’implication des logiciens est – sémantiquement – très exactement celle qu’utilisent les mathématiciens.)

Il faut donc que la proposition «4 est pair» puisse être considérée comme résultant de l’attribution à l’objet 4 de la propriété de parité. Dès lors que la parité est un prédicat P à une variable x , les quantifications sur cette variable deviennent possibles:

D’où le terme de «théorie de la quantification» qui a longtemps désigné le calcul des prédicats, ou plus précisément sa partie non propositionnelle.

Nécessaire à la formalisation du discours mathématique, le calcul des prédicats du premier ordre est-il suffisant? La réponse est moins tranchée – nous y reviendrons à la fin de cet article. Indiquons d’emblée que «le» calcul des prédicats du premier ordre ne désigne pas un langage unique, mais une infinité de langages aux différences significatives, chacun étant adapté à l’étude d’une famille déterminée de structures mathématiques de par son vocabulaire (les règles syntaxiques et sémantiques étant uniformes, comme nous allons le voir).

Morphologie

Un langage du premier ordre L a pour vocabulaire une réunion disjointe d’ensembles V, C, Q (essentiellement communs à tous les langages) et face=F9796 R, face=F9796 , face=F9796 C (caractéristiques de L). On se donne:

– V =v ⁿ ; n 捻 N, ensemble dénombrable dit ensemble des variables (formelles) ;

– C, ensemble des connecteurs (nous choisirons C =囹, 轢參);

– Q, ensemble des quantificateurs (il en existe deux: le quantificateur universel 葉 et le quantificateur existentiel 說; en pratique, on n’en prend souvent qu’un seul comme symbole primitif – nous choisirons Q =葉參);

– face=F9796 R = 聆 face=F9796 Rⁿ , face=F9796 Rⁿ étant l’ensemble (peutn 閭1être vide) des symboles de relation n-aires (ou à n places );

– face=F9796 F = 聆 face=F9796 Fⁿ , face=F9796 Fⁿ étant l’ensemble (peuth 閭1être vide) des symboles d’opération (ou de fonction ) n-aires (ou à n places ou arguments );

– face=F9796 C, l’ensemble (peut-être vide) des symboles de constante (ou d’individu ).

Pour la plupart des langages L utilisés en pratique, l’ensemble face=F9796 R 聆 face=F9796 F 聆 face=F9796 C (appelé parfois ensemble des symboles non logiques de L, ou type de L) est fini. C’est le cas du langage de la théorie des ensembles (du premier ordre à un type d’objet), L^ens, qui comprend deux symboles de relation binaire, 年 (symbole d’égalité formelle) et 捻 (symbole d’appartenance) [cf. théorie axiomatique des ENSEMBLES]. Le même langage peut servir à l’étude de n’importe quelle famille de structures munies d’une relation binaire (par exemple les structures d’ordre). Un autre langage important est le langage L^ar couramment utilisé pour l’arithmétique; il comprend un symbole de relation binaire 年, deux symboles d’opération binaire + et x et deux symboles de constante, 0 et 1. La plupart des langages utilisés en mathématiques (il n’en est pas de même en informatique) sont égalitaires , c’est-à-dire comprennent un symbole de relation binaire distingué appelé symbole d’égalité . Enfin, il est parfois commode de se passer de symboles d’opération; on se ramène à ce cas en remplaçant chaque symbole d’opération n -aire f par un symbole de relation (n + 1)-aire R^f , destiné à être interprété comme le graphe de la fonction qui interpréte f – naturellement des dispositions syntaxiques et sémantiques sont prises pour qu’il en soit ainsi.

Les termes de L, qui seront interprétés par les éléments d’une structure, sont:

– les éléments de V et ceux de face=F9796 C;

– les suites finies de la forme t = (f ) 惡t ¹, size=1^惡 ... size=1^惡t ⁿ , où f 捻 face=F9796 Fⁿ , t ¹, ..., t ⁿ sont des termes et a size=1^惡b désigne la suite obtenue en concaténant les suites a et b dans cet ordre; on note t , plus simplement, ft ¹...t ⁿ .

L’ensemble face=F9796 ^L des termes de L peut donc être considéré comme la réunion 聆 face=F9796 Tⁿ des n 閭0ensembles des termes de complexité 0 (V 聆 face=F9796 C), 1, ..., n , ... Ainsi, les termes de L^ens sont (uniquement) les variables, tandis que les termes de L^ar sont les variables et les constantes 0 et 1 (complexité 0), puis les suites de la forme + v ⁱ v ^j , x v ⁱ v ^j , + 0v ^ij , + 1v ⁱ , x 0v ⁱ , x 1v ⁱ , + v ⁱ 0, etc. (complexité 1), puis par exemple + x v ⁱ v ^j + 1v ^k , x + 1 + 0, etc. (complexité 2)... Si l’on convient d’écrire a + b au lieu de + ab et a x b au lieu de x ab , et d’utiliser les parenthèses à la manière habituelle, on voit par exemple que les deux derniers termes se lisent (v ⁱ x v ^j ) + (1 + v ^k ) et (1 + 1) x (0 + 0).

Les formules de L sont:

– les formules atomiques, de la forme (R) size=1^惡t ¹, size=1^惡 ..., size=1^惡t ⁿ (noté simplement Rt ¹...t ⁿ ), où R 捻 face=F9796 Rⁿ et t ⁿ 捻 face=F9796 ^L. Par exemple, dans L^ens comme dans L^ar, les formules atomiques ont la forme 年 t ¹t ², noté encore t ¹ 年 t ²;

– les formules de la forme 囹F et (FG), où F et G sont des formules;

– les formules de la formes 葉v ⁱ F, où v ⁱ 捻 V et F est une formule.

Les autres connecteurs, ici, sont dérivés, comme dans notre version du calcul propositionnel. De même, la notation 說v ⁱ F abrège (ici) 囹(face=F0019 葉v ⁱ 囹F).

La notion de variable donne lieu à une distinction morphologique cruciale: celle d’occurrence libre et d’occurrence liée . Une occurrence d’une variable v dans une formule F est un couple formé de la variable v et d’une place dans F où v apparaît non immédiatement précédée d’un quantificateur. L’idée, très simple, est qu’une occurrence est libre tant qu’une quantification ne vient pas la lier, tandis qu’une quantification 葉v ⁿ ou 說v ⁿ placée devant une formule G lie (on dit aussi mutifie ) toutes les occurrences libres de v ⁿ dans G. Ainsi, dans la formule de L^ar:

toutes les occurrences de v ⁱ sont liées, la première occurrence de v ^j est liée, la seconde libre, et toutes les occurrences de v ^k sont libres. Une variable libre d’une formule F est une variable ayant au moins une occurrence libre dans F. Un énoncé ou formule close est une formule sans variable libre.

Syntaxe

Les preuves sont construites à partir d’axiomes à l’aide de règles d’inférence, comme dans le calcul propositionnel.

Les axiomes sont d’une part, comme en calcul propositionnel, les formules de la forme ( 見), ( 廓), ( 塚) (mais naturellement les formules A, B, C qui y figurent sont ici des formules du langage L); d’autre part les formules de la forme:

( 嗀) (face=F0019 葉v (AB))(A(face=F0019 葉v B)), où A et B sont des formules de L et v une variable qui n’est pas libre dans A.

( 﨎) (face=F0019 葉v A(v ))A(t ), où A(v ) est une formule, t un terme ne contenant aucune variable liée dans A(v ), et A(t ) résulte de la substitution de t à toute occurrence libre de v dans A(v ).

Les règles d’inférence sont d’une part le modus ponens , d’autre part la règle de généralisation : pour toute formule A et toute variable v , de A on infère 葉v A.

À partir de là, toutes les définitions syntaxiques données pour le calcul propositionnel s’étendent au calcul des prédicats. Ici encore, de nombreuses variantes sont possibles, ainsi que des systèmes de déduction naturelle.

Sémantique

Depuis l’introduction des «mathématiques modernes», tout lycéen a (ou devrait avoir) une première idée assez claire de la sémantique des langages du premier ordre: il saisit en effet en quel sens l’«axiome» 葉x 葉y x ^{y = y x est «vérifié» quand «représente» la multiplication dans l’ensemble Z des entiers relatifs, et ne l’est pas quand représente la soustraction dans Z. Ce qui lui manque en revanche, c’est d’une part un ensemble de règles précises permettant de déterminer la valeur de vérité d’une formule complexe à partir des formules plus simples qui la composent – il n’en a bien entendu nul besoin; d’autre part, une idée de ce qui s’exprime ou ne s’exprime pas dans un langage du premier ordre donné – ainsi la formule 說n 捻 N 葉x x n = 1 n’est pas une formule de Lar (indépendamment des notations), en raison de la quantification existentielle relativisée à N. Nous reviendrons sur cette question au chapitre Au-delà du premier ordre . Un exposé complet de la première alourdirait inutilement cet article; nous nous contenterons de quelques indications, laissant de côté les complications techniques.}

Le langage L a pour domaine d’interprétation une collection de structures appelées L-structures (ou réalisations du langage L). Une L-structure face=F9828 a comprend:

– un ensemble non vide A appelé univers ou ensemble de base ;

– pour chaque symbole de relation n -aire R de L, une relation à n places sur A, 漣R face=F9828 size=1^a, c’est-à-dire un sous-ensemble de Aⁿ ;

– pour chaque symbole d’opération n -aire f de L, une application 肋 face=F9828 size=1^a de Aⁿ dans A;

– pour chaque symbole de constante c de L, un élément 縷 face=F9828 size=1^a de A.

Quand L est un langage égalitaire, on se restreint en général aux L-structures égalitaires , c’est-à-dire celles dans lesquelles le symbole d’égalité est interprété par l’égalité dans l’univers A (la diagonale de A 憐 A).

En quel sens peut-on dire qu’un énoncé 﨏 de L prend la valeur vrai, ou encore est vérifié ou satisfait dans face=F9828 a? Un exemple en donnera une idée: soit 﨏 l’énoncé de L^ar:

Il est satisfait dans une L^ar-structure face=F9828 a si et seulement si: pour tout élément a ¹ de A il existe un élément a ² de A tel que 漣x face=F9828 a (a ¹, a ²) = 路 face=F9828 a. Par exemple, si face=F9828 a est la structure égalitaire d’univers N (resp. Q, ensemble des rationnels non nuls) dans laquelle 路 face=F9828 size=1^a est 1 et 漣x face=F9828 a la multiplication ordinaire, alors face=F9828 a ne satisfait pas (resp. satisfait) 﨏.

La difficulté est de comprendre en quel sens la valeur de 﨏 dépend de celle de sa sous-formule 祥: face=F0019 說v ² xv ¹v ² 年 1. Elle est résolue, en gros, par l’attribution à la formule non close 祥 d’une valeur 漣 祥 face=F9828 size=1^a qui est [quelque chose comme] l’ensemble des a ¹ 捻 A tels qu’il existe un a ² 捻 A tel que 漣x face=F9828 size=1^a (a ¹, a ²) = 路 face=F9828 size=1^a; l’énoncé 﨏 est vérifié si et seulement si pour tout a ¹ 捻 A, a ¹ appartient à 漣 祥 face=F9828 size=1^a.

À partir de là, si l’on se restreint aux énoncés, toutes les définitions sémantiques données pour le calcul propositionnel se généralisent. La notion de base est celle de modèle d’un énoncé ou d’un ensemble d’énoncés: c’est une L-structure dans laquelle ce ou ces énoncés sont vérifiés.

Complétude et compacité

Les théorèmes de complétude, de complétude forte et de compacité pour le calcul des prédicats s’énoncent exactement de la même façon que pour le calcul propositionnel. (Le théorème de complétude est dû à Gödel – 1930 –, ainsi que les théorèmes de complétude forte et de compacité pour les langages dénombrables; ces deux derniers résultats ont été étendus aux langages quelconques par L. Henkin – 1949 – et A. I. Mal’cev – 1936 – respectivement.) Ces énoncés revêtent cependant ici une tout autre importance, non seulement parce qu’ils portent sur des langages plus puissants, mais aussi parce que leurs diverses démonstrations reposent sur des méthodes fécondes. Ainsi, la démonstration de Henkin de la complétude forte inaugure-t-elle l’une des principales méthodes de la théorie des modèles (cf. théorie des MODÈLES). Elle consiste à se ramener au calcul propositionnel, en éliminant les quantificateurs par l’introduction, pour chaque formule de la forme 說v 﨏(v ), d’un symbole de constante spécifique c size=1^﨏, appelé témoin , et de l’axiome 說 v 﨏(v )﨏(c size=1^﨏).

Dans la pratique, on utilise généralement des versions égalitaires de ces théorèmes fondamentaux. Il découle facilement, par exemple, du théorème de complétude, qu’un énoncé d’un langage égalitaire L est satisfait dans toute L-structure égalitaire si et seulement si il est conséquence (formelle) d’un ensemble face=F9796 E^L de formules appelées axiomes de l’égalité , et qui sont (par exemple) toutes les formules de la forme:

où v ⁱ , v ^j , v ^k sont des variables.

où les v ^{i k} et v ^{j k} sont des variables, R un symbole de relation n -aire.

où t (v ^{i 1} ... v ^{i n} ) est un terme contenant des variables v ^{i 1}, ..., v ^{i n} , et t (v ^{j 1} ... v ^{j n} ) s’obtient en y substituant v ^{j 1} à v ^{i 1}, etc.

À titre d’exemple d’application du théorème de compacité égalitaire, mentionnons l’existence d’un modèle non standard de l’arithmétique (i.e. une L^ar-structure non isomorphe à N) –résultat obtenu à l’origine par T. Skolem à l’aide des ultraproduits (cf. théorie des MODÈLES).

Théories

Ces préliminaires essentiels établis, les logiciens sont rapidement amenés à quitter le calcul des prédicats dit pur pour l’étude des «calculs» plus spécialisés que sont les théories du premier ordre . Une théorie dans un langage du premier ordre L est simplement un ensemble d’énoncés de L, dont on suppose en général qu’il est cohérent (au sens défini à propos du calcul propositionnel), ou encore (c’est équivalent en vertu du théorème de complétude forte) qu’il admet un modèle. Du point de vue syntaxique, les énoncés de font figure d’axiomes «spécifiques» dont on dispose dans le cadre de la théorie. Du point de vue sémantique, on restreint la collection des L-structures à celle (non vide) des modèles de . Les théorèmes d’une théorie sont ses conséquences (formelles ou tautologiques). Une théorie peut être donnée explicitement (on dispose – au moins potentiellement – d’une liste de ses axiomes), ou bien implicitement: on considère souvent la théorie d’une L-structure donnée, c’est-à-dire l’ensemble des énoncés vérifiés dans cette structure, ou encore la théorie d’une collection de structures , ensemble des énoncés vérifiés dans chaque structure de la collection. On trouvera des exemples dans les chapitres Effectivité, décidabilité et Les théorèmes de limitation.

À côté des théorèmes de complétude et de compacité, un théorème élémentaire, dû à Löwenheim et Skolem (1915-1922), joue ici un rôle essentiel: toute théorie du premier ordre dans un langage dénombrable qui admet un modèle infini admet un modèle dénombrable. L’étude sémantique des théories du premier ordre se fonde sur ces résultats, et constitue le cœur de la théorie des modèles («théorie» étant pris au sens courant). Pour la suite (sémantique) de cette histoire, on se reportera donc à l’article théorie des MODÈLES.

Effectivité, décidabilité

La notion de méthode effective de calcul, ou encore d’algorithme , accompagne les mathématiques depuis les origines. Soit (Pⁱ )i 捻I une famille de problèmes formulés en termes mathématiques, telle que, pour chaque i de I, le problème Pⁱ admette une réponse Rⁱ . Un algorithme pour la famille (Pⁱ )ⁱ size=1^捻I peut être décrit comme une méthode, c’est-à-dire un ensemble d’instructions absolument précises (ou encore un programme) permettant à un homme agissant mécaniquement, sans recours à d’autres facultés que celles de tracer et d’identifier des inscriptions et de reconnaître la conformité littérale des opérations qu’il effectue aux instructions qu’il suit, d’obtenir, à partir de la donnée d’un élément quelconque i de I, la réponse Rⁱ en un nombre fini d’étapes. (cf. ALGORITHMIQUE.)

Naturellement la question se pose de savoir si cette «définition» a le moindre sens – un exercice amusant consisterait à y relever les obscurités et ambiguïtés de tous ordres. Il est sûrement possible d’en éliminer certaines, mais dans l’état présent de nos connaissances il est improbable qu’on puisse donner une définition indiscutable de ce qu’est pour l’esprit humain en général de fonctionner «comme une machine» (mathématique).

Il est cependant remarquable que les mathématiciens s’accordent sans difficulté, l’expérience le prouve ^{[cf. ALGORITHMIQUE]}, pour attribuer ou refuser à quelque méthode particulière qu’on ait pu leur proposer la qualité d’algorithme. Les opérations sur les nombres entiers ou décimaux enseignées à l’école primaire, l’algorithme d’Euclide pour la détermination du plus grand commun diviseur de deux entiers, ou de deux polynômes, les méthodes classiques pour différencier une fonction obtenue à partir des fonctions classiques de l’analyse, ou pour intégrer une fraction rationnelle, etc., sont des méthodes reconnues pour effectives. Il existe donc une stabilité empirique du concept métamathématique d’effectivité.

On peut dès lors se demander: primo s’il est utile de poursuivre l’analyse de cette notion; secundo à quel type de réponse on peut espérer parvenir; tertio ce que la logique mathématique a à voir dans cette affaire.

Objets de l’effectivité: fonctions, ensembles, théories

Avant de répondre, il est utile de classer les familles de problèmes pour lesquelles on recherche des méthodes effectives de résolution, ce qui revient à déplacer l’attention des méthodes elles-mêmes aux classes d’objets accessibles ou constructibles par ces méthodes. Le cas le plus important, car les autres s’y ramènent, est celui des fonctions de N^p dans N: une telle fonction f est (effectivement) calculable s’il existe un algorithme pour la classe des problèmes (valeur de f ( 讀 )?) 讀 捻 N^p . On peut également partir des sous-ensembles de N^p : X 裂 N^p est décidable s’il existe un algorithme pour la classe de problèmes ( 讀 捻 X?) size=1^讀 size=1^{捻 N}p . Un sous-ensemble est décidable si et seulement si sa fonction caractéristique est calculable. Inversement, une fonction est calculable si et seulement si son graphe est décidable. Une notion dérivée mais essentielle est celle de sous-ensemble semi-décidable de N^p : c’est l’image d’une fonction calculable, ou bien l’ensemble vide. Dire que X est un ensemble semi-décidable, c’est dire qu’il existe pour la classe de problèmes ( 讀 捻 X?) size=1^讀 size=1^{捻 N}p une méthode, dite semi-effective , qui, si n 捻 X, fournit la réponse «oui», et, si n 殮 X, ou bien fournit la réponse «non» ou bien ne fournit pas de réponse (la suite des opérations ne prenant jamais fin). Il est facile de voir qu’un ensemble X est décidable si et seulement si X et son complémentaire sont semidécidables.

Enfin, un système formel face=F9796 S – ou une théorie de face=F9796 S – est décidable (resp. semi-décidable) si la classe de problèmes (face=F0019 塞 face=F9796 size=1^S 﨏?) 漣 ( 塞 face=F9796 size=1^S 﨏?) 漣, 﨏 parcourant l’ensemble des formules (closes) de face=F9796 S, est décidable (resp. semi-décidable). Pour les langages formels usuels, notamment les langages du premier ordre, nous verrons qu’il est possible de coder par des entiers naturels les formules de face=F9796 S, et cela de manière effective. L’ensemble des théorèmes de face=F9796 S (ou de ) est alors remplacé par un sous-ensemble T de N, et face=F9796 S (ou ) est décidable (resp. semi-décidable) si et seulement si T l’est.

La classe des fonctions récursives

Revenons maintenant à nos trois questions:

– primo , l’utilité d’une définition précise et générale de l’effectivité est qu’elle permet d’établir des résultats négatifs, c’est-à-dire de démontrer qu’il n’existe pas d’algorithme (au sens restreint de la définition en question) pour une classe de problèmes donnée.

– secundo , la logique mathématique (c’est là, selon G. Kreisel par exemple, l’une de ses principales contributions à la philosophie des mathématiques) a su résoudre le problème épistémologique de la nature d’une réponse en apportant une réponse pleinement satisfaisante parce qu’indépendante de tout formalisme particulier: elle a créé la notion de fonction récursive , et s’est fondée sur la remarquable stabilité de cette notion pour la proposer comme équivalent mathématique de la notion intuitive de fonction calculable.

En effet, à partir de 1931, toute une série de logiciens (Gödel, Herbrand, Church, Kleene, Turing, Post, Markov) définissent des classes de fonctions d’entiers dans les entiers par des moyens extrêmement différents, et montrent que:

1. Toutes les fonctions ainsi définies sont manifestement calculables.

2. Toute fonction calculable imaginée à ce jour appartient à chacune des classes ainsi définies.

3. Toutes ces classes coïncident.

Ces trois constatations (dont les deux premières sont démontrables «informellement», la troisième, la plus frappante, étant un théorème mathématique stricto sensu ) conduisent A. Church à proposer dès 1936 sa célèbre thèse, selon laquelle toute fonction calculable est une fonction récursive, c’est-à-dire subsumée par les définitions mathématiques de Gödel et al. (l’inverse étant manifestement vrai). Cette équivalence entre un concept intuitif et un concept mathématique ne peut évidemment pas faire l’objet d’un théorème, mais seulement d’une thèse métamathématique. Presque universellement adoptée, elle n’est naturellement pas indispensable au développement de la théorie mathématique de la récursivité et de ses applications. Son rôle est d’une part heuristique, car elle permet de substituer dans les raisonnements la notion intuitive d’effectivité aux définitions techniques de récursivité, beaucoup moins maniables; d’autre part interprétatif, puisqu’elle implique qu’un résultat négatif (la non-récursivité d’une fonction) signifie l’impossibilité de jamais exhiber un algorithme pour cette fonction.

En 1942, A. Turing définit une machine abstraite (qui porte désormais son nom) et, ayant montré que les fonctions calculables au moyen de cette machine sont exactement les fonctions récursives ^{[cf. RÉCURSIVITÉ]}, propose de considérer que toute fonction calculable par quelque machine que l’on puisse imaginer est calculable par sa machine. Combinées, les thèses de Church et de Turing sont donc exprimées par la double égalité: récursif = calculable par l’homme = calculable par (tout) ordinateur.

Pour les sous-ensembles de N^p , l’homologue mathématique de «décidable» est récursif , celui de «semi-décidable» récursivement énumérable .

Logique et récursivité

Tertio , la logique mathématique est intimement liée dès l’origine à la théorie de l’effectivité. En effet (cf. théorie de la DÉMONSTRATION et problèmes de HILBERT), D. Hilbert entendait prouver la décidabilité de l’arithmétique (convenablement formalisée), et celle de toute théorie mathématique. De la solution découlerait également, pensait-il, une démonstration de cohérence de l’arithmétique, et partant de l’ensemble des mathématiques. À ce programme qui porte le nom de Hilbert (et aux travaux de son école), la logique mathématique contemporaine, dans une grande mesure, doit d’exister – paradoxalement, puisque c’est en ruinant le programme qu’elle a acquis sa notoriété. Gödel, on le sait, établit l’indécidabilité de l’arithmétique (cf. Les théorèmes de limitation ). Pour ce faire, il lui faut une notion de fonction récursive: sa première définition (qui recouvre en fait une classe restreinte, celles des fonctions récursives primitives ) fonde une théorie extraordinairement féconde, aux généralisations étonnantes, qui fait historiquement partie de la logique, et puise en maints endroits aux méthodes de la logique. De même, l’étude des principales théories algébriques sous l’angle de la décidabilité constitue une branche importante de la logique. Enfin, inversement, la récursivité et certaines de ses généralisations interviennent de manière toujours plus importante en théorie de la démonstration, en théorie des modèles et en théorie des ensembles.

Calcul propositionnel et calcul des prédicats: propriétés de décidabilité

Le calcul propositionnel et le calcul des prédicats du premier ordre sont semi-décidables. Cela résulte, dans chaque cas, de ce que, d’une part, l’ensemble des axiomes est décidable, et, d’autre part, les applications qui à une ou à deux formules associent leur conséquence par une des règles d’inférence sont calculables. (Il faut naturellement supposer, dans le cas d’un langage du premier ordre, que l’alphabet est décidable, ce qui est toujours vérifié.) On peut dès lors facilement construire une fonction calculable de N dans N dont l’image est l’ensemble des [numéros de code de] théorèmes du calcul considéré. De façon plus concrète, on peut imaginer une «machine à déduire», munie d’une énumération des axiomes, qui produirait une énumération de toutes les preuves possibles (la machine serait programmée en sorte que toute preuve soit produite en un rang fini, ce qui exige quelques précautions dans la manière dont on fait défiler les possibilités potentiellement infinies telles que les substitutions). Pour savoir si une formule [close] donnée est un théorème, on mettrait la machine en route et on comparerait, à chaque étape, la dernière formule obtenue à la formule donnée.

Le calcul propositionnel est même décidable. Cela résulte d’emblée du théorème de complétude et du fait qu’une formule à p variables propositionnelles s’interprète comme une fonction de0, 1^p dans0, 1 qui est calculable, puisque de graphe fini – le calcul de ses 2^p valeurs permet de déterminer s’il s’agit ou non d’une tautologie, donc d’un théorème. La première démonstration (Post, 1921), purement syntaxique, consiste à ramener, de manière effective, la formule donnée à une forme canonique équivalente dont la prouvabilité éventuelle est patente.

Au contraire, le calcul des prédicats est indécidable – plus exactement, tout langage du premier ordre, sauf s’il ne comprend que des symboles de relation unaire et des constantes, est indécidable. Ce résultat, qui s’étend aux langages égalitaires, est dû à Church (1936) et est apparenté aux autres grands théorèmes de limitation découverts à l’époque (cf. Les théorèmes de limitation ). Il entraîne une solution négative à l’Entscheidungsproblem de Hilbert pour tous les langages (non monadiques); la classe de problèmes ( 塞 﨏?), où parcourt l’ensemble des ensembles finis de formules du langage et 﨏 l’ensemble des formules, est indécidable.

En revanche, le caractère semi-décidable du calcul des prédicats peut être précisé, grâce à un très important théorème dû à Herbrand (1929). Soit dans un langage L une formule sans quantificateur à n variables libres v ¹, ..., v ⁿ : 﨏 (v ¹, ..., v ⁿ ). L’énoncé 說v ¹ ... 說v ⁿ 﨏 (v ¹, ..., v ⁿ ) est prouvable si et seulement si il existe des n -uples de termes de L, (t ¹¹, ..., t ¹ⁿ ), ..., (t ^1k , ..., t ^{n k} ) tels que la formule 﨏(t ¹¹, ..., t ¹ⁿ ) 鈴 ... 鈴 﨏(t ^1k , ..., t ^{n k} ) soit prouvable dans le calcul propositionnel construit sur les formules sans quantificateur de L. Sur ce théorème, très proche de résultats de Gentzen (cf. théorie de la DÉMONSTRATION), se fondent des méthodes de démonstration automatique étudiées en informatique théorique.

Autres résultats de décidabilité

Il existe un grand nombre de résultats établissant la décidabilité ou l’indécidabilité d’importantes théories (ou classes de problèmes) algébriques. Beaucoup sont établis non pas directement, mais par transfert sur des théories connues: si l’on parvient à «traduire» de manière effective les énoncés d’un langage L¹ en énoncés d’un langage L², en sorte que, pour tout énoncé 﨏 de L¹, 﨏 est un théorème d’une théorie ¹ de L¹ si et seulement si sa traduction est un théorème d’une théorie ² de L², alors la décidabilité de ² entraîne celle de ¹.

La principale méthode directe pour établir la décidabilité d’une théorie , la première en date, consiste à «éliminer» les quantificateurs de toute formule du langage, modulo , de manière effective; il suffit alors de trouver une méthode de décision pour les formules sans quantificateur, ce qui est beaucoup plus facile. On a pu établir de cette manière la décidabilité de la théorie de la structure d’ordre des entiers naturels (C. H. Langford, 1927); de la théorie de la structure additive des entiers naturels (M. Presburger, 1929); de la théorie des algèbres de Boole (A. Tarski, 1949); de la théorie du corps ordonné des réels, et par là celle de la géométrie élémentaire, c’est-à-dire euclidienne plane (c’est l’un des plus beaux résultats; publié en 1948 seulement par Tarski, il est connu de lui, mais aussi de Gödel et de Herbrand dès 1930); de la théorie des groupes abéliens (W. Smielev, 1955); de la théorie des corps algébriquement clos; de la théorie des ordres denses; etc.

À cette méthode d’esprit [plutôt] syntaxique s’opposent des méthodes purement sémantiques, qui permettent de retrouver, parfois de manière plus rapide, certains des résultats précédents, et de résoudre, d’autres problèmes parfois très difficiles: décidabilité de la théorie des corps p -adiques (J. Ax et S. Kochen, 1965) et de la théorie des corps finis (Ax, 1968, cf. théorie des MODÈLES).

Les résultats d’indécidabilité sont souvent liés, on l’a dit, aux théorèmes d’incomplétude (cf. Les théorèmes de limitation et RÉCURSI- VITÉ, chap. 4) – soit directement, soit par une variante de la méthode du transfert (existence d’une extension cohérente commune à la théorie étudiée et à une théorie «très» indécidable – à l’indécidabilité très contagieuse: nous ne préciserons pas davantage). Ainsi se démontre l’indécidabilité de la théorie des groupes et de celle des treillis (Tarski, 1953).

Nous mentionnerons ici, pour conclure cette section, un résultat d’indécidabilité doublement marquant: d’une part, c’est le premier théorème négatif portant sur un problème excessivement simple formulé en dehors de toute préoccupation logique ou métamathématique; d’autre part, le problème a été posé (par Thue, en 1914) longtemps avant qu’on ne dispose de l’outil conceptuel nécessaire à sa solution.

On considère un alphabet fini A et un ensemble fini P de couples de mots (suites finies) de A. On définit sur l’ensemble face=F9828 mA des mots de A la relation d’équivalence 黎 telle que s 黎 t si et seulement si il existe s ¹, u , s ², t ¹, v , t ² tels que:

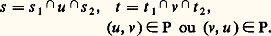
L’ensemble-quotient G = face=F9828 mA/ 黎 muni de la concaténation est un semi-groupe , P une présentation de G, les éléments de A les générateurs de la présentation P. Le problème des mots pour le semi-groupe finiment présenté (G, P) est de reconnaître, étant donné deux mots quelconques, s’ils sont équivalents (c’est-à-dire s’ils représentent le même élément de G). Post et Markov ont démontré indépendamment en 1947 qu’il existe un semi-groupe finiment présenté dont le problème des mots est indécidable. A fortiori, le problème des mots pour [tous] les semi-groupes est-il indécidable. Un résultat analogue, mais beaucoup plus difficile, est que le problème des mots pour les groupes finiment présentés est indécidable (P. S. Novikov, 1955; W. W. Boone, 1957).

Les théorèmes de limitation

Les grands théorèmes négatifs de la période 1931-1936 marquent de différentes façons les limites des capacités descriptives et démonstratives des systèmes formels. Ils concernent en fait au premier chef l’arithmétique, dont on connaît le rôle central au sein des mathématiques.

Nous nous restreindrons donc dans cette section au langage L^ar précédemment défini auquel, par commodité, nous adjoignons un symbole d’opération unaire s. Toute mention d’une formule, d’une théorie, d’une structure sous-entend la référence à ce langage. Le modèle standard de l’arithmétique est la structure face=F9828 n d’univers N muni de l’addition et de la multiplication usuelles, de la fonction successeur 丹 face=F9828 size=1ⁿ = suc : n 料n + 1, et des éléments distingués 漣0 face=F9828 size=1ⁿ = 0 et 漣1 face=F9828 size=1ⁿ = 1. D’autre part, une théorie est dite axiomatisable si elle admet un ensemble décidable d’axiomes; complète si elle permet de prouver ou de réfuter tout énoncé.

Les théorèmes négatifs sur l’arithmétique formelle peuvent alors être approximativement formulés ainsi:

a. Toute théorie dont face=F9828 n est un modèle est indécidable (théorème de Church-Rosser amélioré).

b. L’ensemble des énoncés vrais dans face=F9828 n est indéfinissable arithmétiquement (théorème de Tarski).

c. Toute théorie axiomatisable même rudimentaire est incomplète (premier théorème d’incomplétude de Gödel).

d. Toute théorie axiomatisable suffisamment développée ne permet pas de prouver sa propre cohérence (second théorème d’incomplétude de Gödel).

Ces assertions peuvent être ordonnées, précisées (pour les deux dernières) et démontrées de bien des façons, dont aucune sans doute n’épuise tout à fait la signification de ces phénomènes d’«autolimitation». Nous tenterons de présenter les idées principales, sans chercher à être complet ni à donner les meilleurs résultats possibles.

Codage gödelien

Une étape préliminaire consiste à définir une application x 料 掠x 亮 de l’ensemble des symboles, des formules et des suites de formules à valeurs dans N qui soit, d’une part, injective, d’autre part, calculable au sens où l’on puisse, étant donné x , calculer effectivement 掠x 亮 et, étant donné un entier n , établir effectivement s’il existe un x tel que n = 掠x 亮 et, dans ce cas, déterminer effectivement cet x . On peut procéder de diverses façons pour construire une telle fonction. Gödel ayant inventé la première, on appelle nombre de Gödel (n.g.) de x l’entier 掠x 亮. Ce codage rend possible une autoréférence non paradoxale dans L^ar.

Représentation des ensembles et des fonctions

Une seconde idée consiste à représenter un sous-ensemble X de N par une formule 﨏(v ) à une variable libre v telle que, pour tout entier n , n désignant le terme ss ... s0 (où s figure n fois), on ait 塞 﨏(n) si et seulement si n 捻 X et 塞 囹 﨏(n) si et seulement si n 殮 X. La théorie varie suivant les besoins. Naturellement, pour une théorie donnée , tout ensemble X ne rend pas la chose possible (comme le montre un argument élémentaire de cardinalité); ceux pour lesquels une telle formule existe sont dits représentables dans . Quand est la théorie de face=F9828 n, autrement dit quand 塞 﨏 signifie face=F9828 n |= 﨏, on dit que X est arithmétique .

On étend cette définition, de manière évidente, aux sous-ensembles de N^p pour p 礪 1, puis (en passant par les graphes) aux applications de N^p dans N pour p 閭 1.

Nous admettrons qu’une fonction récursive est arithmétique (cf. RÉCURSIVITÉ, où l’on montre qu’elle est même représentable par une formule de faible complexité).

Le théorème de Tarski

Un argument diagonal établit d’abord le lemme suivant: il n’existe pas de sous-ensemble arithmétique R de N² qui énumère les sous-ensembles arithmétiques de N au sens où, pour chaque X 裂 N arithmétique, il existerait un entier x (le R-code de X) tel que, pour tout entier n , on ait (n , x ) 捻 R si et seulement si n 捻 X. En effet, s’il existait un tel R, il serait représenté par une formule 﨏(v ¹, v ²) à deux variables libres; la formule 囹 﨏(v , v ) représenterait un sous-ensemble arithmétique X de N dont le R-code serait un entier x tel que (x , x ) 捻 R équivaudrait à x 捻 X, donc face=F9828 n |= 﨏(x, x) à face=F9828 n |= 囹 﨏(x, x).

Soit maintenant A l’ensemble des n.g. d’énoncés vrais dans face=F9828 n.

Supposons que A soit arithmétique, et représenté par la formule 見(v ). Considérons d’autre part la fonction h qui, à un couple d’entiers (m , n ) tel que m soit le n.g. d’une formule 﨏(v ) à une variable libre v , associe le n.g. de la formule 﨏(n): h (face=F0019 掠 﨏(v ) 亮, n ) = 掠 﨏(n) 亮. Cette fonction, qui n’est pas définie partout, est calculable sur son domaine, et comme celui-ci est décidable, elle admet un prolongement partout défini et calculable, donc récursif, donc de graphe représentable par une formule 兀(v ¹, v ², v ³).

Soit enfin X un sous-ensemble arithmétique quelconque de N, représenté par une formule 﨡(v ). On a pour tout entier n : n 捻 X si et seulement si face=F9828 n |= 說v ³[ 見(v ³) 廬 兀(m, n, v ³)] pour m = 掠 﨡(v ) 亮. Si 﨏(m , n ) désigne l’énoncé figurant à droite du signe |=, la formule 﨏(v ¹, v ²) représente un sous-ensemble arithmétique de N², en contradiction avec le lemme: A n’est pas arithmétique, d’où le slogan célèbre: «La vérité (arithmétique) n’est pas définissable (dans l’arithmétique).»

Cette démonstration rappelle le paradoxe du menteur: en raisonnant dans le flou, on voit que l’énoncé 囹 見(face=F0019 掠囹 見 亮) s’interprète dans face=F9828 n comme l’affirmation «Est fausse la formule dont le n.g. est le mien», c’est-à-dire «Je suis fausse.» (Est faux, non moins, ce raisonnement, car le n.g. de 囹 見(face=F0019 掠囹 見 亮) n’est pas celui de 囹 見(v ), puisqu’on a opéré une substitution: d’où la nécessité d’introduire h !)

Le premier théorème d’incomplétude

Au prix d’une semblable entorse à la rigueur, on peut schématiser la démonstration du premier théorème d’incomplétude de la manière suivante. Soit 廓(v ) la formule définissant la propriété «la formule de n.g. v est prouvable». L’énoncé 囹 廓(face=F0019 掠囹 廓 亮), interprété dans face=F9828 n, affirme «Je ne suis pas prouvable.» Si cet énoncé était faux, il serait (vu son interprétation) prouvable, donc vrai; donc cet énoncé est vrai, donc (vu son interprétation) non prouvable.

Cependant, quand on remplace la vérité dans face=F9828 n par la prouvabilité dans une théorie, on ne modifie pas seulement la structure de la démonstration, mais aussi, et de manière importante, ses principales étapes.

Nous adoptons ici la théorie R dont les axiomes sont les suivants (les lettres x et y désignent des variables formelles):

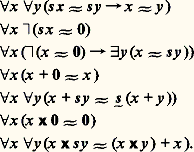
(On n’a pas fait figurer les axiomes de l’égalité pour L^ar, en les supposant adjoints aux axiomes du calcul des prédicats pur.) La théorie R est assez faible puisque non seulement elle ne comprend aucune forme du principe de récurrence, mais que même la commutativité de +, par exemple, ne s’y démontre pas. D’autre part, tous ses axiomes étant vrais dans face=F9828 n, R est cohérente.

La représentabilité d’un ensemble ou d’une fonction se comprend maintenant relativement à R. Or il se trouve que cette condition est trop restrictive pour être utile. La notion adaptée ici est celle d’un sous-ensemble X de N faiblement représentable dans R: il existe une formule 﨏(v ) telle que n 捻 X si et seulement si R 塞 﨏(n). La principale difficulté technique consiste à montrer que l’ensemble des n.g. de formules prouvables dans R est récursivement énumérable et donc faiblement représentable dans R. Nous admettons donc qu’il existe une formule 廓(v ) telle que, pour toute formule 﨏, on a:

L’argument diagonal prend ici la forme suivante: soit 﨏(v ) une formule à une variable libre v ; il existe un énoncé tel que:

En effet, soit (v ) la formule 說w ( 兀(v , v , w ) 廬 﨏(w )); soit m = 掠 (v ) 亮 et 祥 = (m). On a, prouvablement dans R:

car l’unique w tel que 兀(face=F0019 掠 (v) 亮, m,w ) est le n.g. de la formule obtenue en substituant, dans la formule [dont le n.g. est celui de] (v ), m à v , c’est-à-dire le n.g. de (m), soit enfin le n.g. de 祥.

Il reste alors à appliquer ce résultat à la formule 﨏(v ) = 囹 廓(v ): soit 祥 un énoncé tel que:

D’une part, R 塞 祥 entraîne R 塞囹 廓(face=F0019 掠 祥 亮) par (2) et R 塞 廓(face=F0019 掠 祥 亮) par (1), ce qui contredit la cohérence de R.

D’autre part, R 塞囹 祥 entraîne R 塞 囹(face=F0019 囹 廓(face=F0019 掠 祥 亮)) par (2), donc R 塞 廓(face=F0019 掠 祥 亮), ce qui par (1) entraîne R 塞 祥: contradiction à nouveau.

Ainsi se trouve établie l’incomplétude de R – et même de tout renforcement raisonnable de R, ce qui donne au résultat sa pleine signification: ce n’est pas d’une faiblesse «accidentelle» que résulte l’incomplétude d’une arithmétique formelle, mais précisément de sa force expressive. On aboutit ainsi à une forme du premier théorème d’incomplétude de Gödel (1931) amélioré par Rosser (1936): Pour toute théorie de l’arithmétique, S, axiomatisable, cohérente et de force au moins égale à R, il existe un énoncé 祥 tel que ni 祥 ni 囹 祥 ne sont prouvables dans S.

Deux remarques pour conclure:

1. L’énoncé «indécidable» 祥 est vrai dans face=F9828 n, puisqu’il affirme dans cette structure sa propre indémontrabilité.

2. Cet énoncé est morphologiquement peu complexe: techniquement ⁰¹ (cf. théorie de la DÉMONSTRATION).

Ce fait est décisif pour la démonstration du second théorème d’incomplétude.

Incomplétude et indécidabilité

De phénomènes d’indécidabilité on peut conclure à des phénomènes d’incomplétude, et inversement. C’est ainsi que le théorème de Matijasevitch (indécidabilité du dixième problème de Hilbert – cf. RÉCURSIVITÉ et problèmes de HILBERT) conduit à une forme des théorèmes d’incomplétude de Gödel ^{[cf. RÉCURSIVITÉ]}.

Dans l’autre direction, le premier théorème d’incomplétude montre par exemple que l’ensemble Th face=F9828 n des énoncés vrais dans face=F9828 n est non récursivement énumérable (résultat plus faible que le théorème de Tarski). Mais on peut facilement démontrer mieux en faisant directement appel à la représentabilité faible des ensembles récursifs: si est un sous-ensemble quelconque de Th face=F9828 n, la théorie est indécidable. D’autre part, l’ensemble des (n.g. de) théorèmes d’une extension axiomatisable cohérente de R est un exemple d’ensemble récursivement énumérable non récursif.

Le second théorème d’incomplétude

L’arithmétique de Peano du premier ordre est la théorie P obtenue en adjoignant à R le schéma d’axiome d’induction: pour toute formule 﨏(v ⁰, ..., v ^k ) à (1 + k ) variables libres v ⁰, ..., v ^k , on a dans P l’énoncé:

(Historiquement, l’axiomatisation proposée par Peano ne fait intervenir que la fonction successeur, et surtout n’est pas du premier ordre, du fait que le principe d’induction est postulé pour tout sous-ensemble, et non pas seulement pour les sous-ensembles définissables.) La théorie P est une théorie axiomatisable considérablement plus forte que R, dans laquelle il est notamment possible de représenter fortement les fonctions récursives primitives par des formules de faible complexité et de prouver leurs équations de définition inductive. On peut montrer l’existence dans P d’une preuve d’un énoncé dont l’interprétation dans face=F9828 n est le raisonnement informel invoqué dans la démonstration du premier théorème d’incomplétude pour établir, Q étant une théorie de force au moins égale à R:

où 廓 représente ici le prédicat de prouvabilité dans Q. Autrement dit, on montre, pour P = Q:

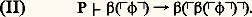
Enfin, on établit la prouvabilité dans P du modus ponens formalisé:

Soit maintenant 﨣 un énoncé contradictoire – par exemple 0 年 1, Coh^P l’énoncé 囹 廓(face=F0019 掠 﨣 亮): interprété dans face=F9828 n, Coh^P exprime la cohérence de P. La démonstration consiste à vérifier que Coh^P est P-prouvablement équivalent à l’énoncé indécidable 祥 du premier théorème d’incomplétude (ce qui établit, soit dit en passant, l’unicité modulo P-équivalence de cet énoncé 祥).

De (2) (avec P au lieu de R) on déduit:

Comme 﨣 est contradictoire, on a:

donc, d’après (I):

d’où, d’après (III):

En rapprochant (a) de (b), on obtient:

Inversement , de (2) on déduit:

d’où, d’après (I):

D’autre part, il vient par (II):

d’où, d’après (d), (III) et un axiome propositionnel:

Comme, propositionnellement, 塞 祥[ 囹 祥( 祥 廬 囹 祥)], par (I) et (III) il vient:

d’où, par (f):

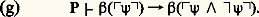
Comme 祥 廬囹 祥 est P-prouvablement équivalent à 﨣, on en déduit facilement de même:

soit enfin, par contraposition et d’après (2):

L’indécidabilité de 祥 entraîne donc celle de Coh^p = 囹 廓(face=F0019 掠 﨣 亮), d’où le second théorème d’incomplétude: L’arithmétique de Peano, si elle est cohérente, ne permet pas de prouver l’énoncé exprimant sa cohérence.

Ce résultat extrêmement frappant appelle quelques remarques:

1. Il s’étend à toute extension axiomatisable de P: ici encore, on ne peut espérer pallier une faiblesse «accidentelle» du système formel choisi.

2. Considéré en dehors de la logique comme capital, le second théorème n’était pour Gödel qu’une «curiosité», comme le rappelle G. Kreisel. Si l’on a vraiment des doutes sur la cohérence d’un système formel particulier, ce n’est certainement pas sur lui qu’on va s’appuyer pour démontrer sa cohérence – car dans un système contradictoire on démontre n’importe quoi!

3. Cependant, le théorème a pour conséquence de rendre peu plausible la découverte d’une démonstration de la cohérence de «la» théorie des ensembles, par exemple celle de Zermelo-Fraenkel (cf. théorie axiomatique des ENSEMBLES). En effet, P se plonge dans ZF (moyennant interprétation). Comme tout procédé mathématique de démonstration imaginé à ce jour est formalisable dans ZF, il en serait ainsi d’une démonstration de cohérence de ZF, ce qui contredit le théorème étendu par la première remarque.

4. Le théorème permet également de détecter les fausses démonstrations de cohérence de l’arithmétique – il y en eut de nombreuses dans les années 1920: dès qu’une démonstration peut se formaliser dans le langage L^ar, elle ne peut qu’être erronée. En revanche, rien n’exclut la possibilité d’une démonstration utilisant des procédés non «élémentaires», c’est-à-dire excédant les capacités expressives de L^ar. De fait, plusieurs démonstrations correctes ont été trouvées, à commencer par celle de Gentzen (1936). Chacune présente un intérêt propre, en ce qu’elle met en jeu des principes de démonstration plus puissants, impliquant pour le mathématicien de «croire» à des objets plus «abstraits» que ceux que le formaliste admet dans son univers. Philosophiquement, la morale est que renoncer à l’abstraction est un sacrifice coûteux et – du moins aux yeux d’un Gödel ou d’un Kreisel – totalement injustifié. Techniquement, toute nouvelle démonstration de cohérence – celle de Gödel (1958) en est un exemple – permet de mieux saisir le sens véritable de résultats et de méthodes élaborés «empiriquement», et d’orienter les recherches en conséquence.

Au-delà du premier ordre

À côté des «faiblesses» relativement cachées que constituent les phénomènes d’incomplétude et d’indécidabilité dont il vient d’être question, la logique du premier ordre en exhibe de beaucoup plus élémentaires, qui pourraient faire douter de son utilité en tant que langage mathématique.

D’une part, certaines propriétés mathématiques importantes d’une L-structure donnée ne sont pas exprimables par un énoncé de L. Il est impossible, par exemple, d’exprimer dans le langage usuel de la théorie des groupes (langage égalitaire à un symbole d’opération binaire) qu’un groupe est infini, ou qu’il est sans torsion. Même un ensemble infini d’énoncés peut ne pas suffire: pour exprimer qu’un groupe est d’ordre fini (quelconque), ou que ses éléments sont en nombre, ou d’ordre, infini (quelconque); ou encore, dans la théorie des ordres, qu’une structure est bien ordonnée; ou encore, dans un langage égalitaire quelconque, qu’une structure est dénombrable.

D’autre part, la logique du premier ordre est incapable de caractériser, à isomorphisme près, une structure infinie donnée. Autrement dit, toute théorie (même infinie) ayant un modèle infini en possède un second non isomorphe au premier. Il existe par exemple une extension non archimédienne du corps des réels R qui vérifie les mêmes énoncés du premier ordre (avec paramètres si l’on veut) que R – d’où la possibilité de l’analyse non standard ^{[cf. ANALYSE NON STANDARD]}, et l’impossibilité concomitante de caractériser au premier ordre dans le langage de l’analyse une classe aussi centrale que les espaces de Hilbert par exemple.

Tous ces phénomènes sont des conséquences simples des théorèmes, eux-mêmes élémentaires, de compacité et de Löwenheim-Skolem.

Comment concilier ces observations avec la conception hilbertienne du premier ordre comme logique «indépassable» des mathématiques? Pour Hilbert, toute hypothèse, tout cadre théorique interne aux mathématiques peut s’expliciter dans un langage du premier ordre convenablement choisi, et toute procédure démonstrative se ramener à une preuve dans un système formel du premier ordre.

La réponse peut sembler assez simple. Dans le langage de la théorie des ensembles, toute propriété ou construction mathématique conçue à ce jour peut en effet s’exprimer, moyennant les axiomes de ZF. On peut par exemple caractériser N, ou R à isomorphisme près. On peut exprimer que deux structures sont isomorphes, qu’une structure est dénombrable, qu’un groupe est de torsion, etc.

Est-ce à dire que la distinction entre ce qui est élémentaire (exprimable au premier ordre) et ce qui ne l’est pas est secondaire au point de s’évanouir dès qu’on adopte le «bon» point de vue? Cette question appellerait une discussion dans laquelle nous ne pouvons entrer ici. Notons seulement qu’en pratique une interprétation des langages «régionaux» dans la langue universelle des mathématiques qu’est L^ens aurait pour premier effet d’encombrer le champ théorique de notions et de problèmes parfaitement intempestifs. Le spécialiste des corps finis n’a pas le moindre doute sur N, et ne se soucie guère de la part que prennent les axiomes de Peano dans ses démonstrations; a fortiori se refuse-t-il à toute inquiétude quant à la cardinalité du continu! Bref, certains présupposés gagnent à ne pas être explicités au premier ordre. Reste à savoir s’il n’y a pas intérêt, dans certains cas, à tenter de les expliciter dans des logiques plus fortes, mieux adaptées à la spécificité de l’objet d’étude.

C’est en partie cette question, en partie la dynamique interne de leur discipline qui ont amené les logiciens à concevoir diverses logiques dites d’ordre supérieur (toutes contiennent en effet le premier ordre), dont certaines ont pris aujourd’hui une certaine, voire une décisive importance. Nous ne parlerons pas des nombreuses logiques d’origine plus ou moins philosophique (plurivalentes, modales, temporelles, déontiques, épistémiques, etc.) dont l’intérêt mathématique est demeuré marginal (le cas tout à fait singulier de l’intuitionnisme fait l’objet d’un article particulier).

Les logiques à plusieurs types d’objets constituent des extensions assez faibles du premier ordre. Elles comprennent plusieurs espèces de variables, et les structures sont de la forme 麗 face=F9828 a¹ ..., face=F9828 aⁿ , ... Rⁱ , ... f ^j , ... 礪, chaque face=F9828 a^k étant une structure au sens habituel, correspondant au k ^e type d’objet, et les Rⁱ , f ^j étant des relations, des fonctions sur la réunion des univers A^k . La logique à deux types d’objets fournit un cadre naturel, par exemple, à la théorie des espaces vectoriels ou à la théorie des ensembles avec classes (NBG...).

Quand, dans une logique à deux types d’objets, on se restreint aux structures dont le deuxième univers prend une valeur fixe face=F9828 m, on obtient la face=F9828 m-logique. L’exemple le plus important est celui où face=F9828 m est le modèle standard de l’arithmétique; on parle alors de 諸-logique (cf. théorie de la DÉMONSTRATION). Ces logiques sont sensiblement plus fortes que le premier ordre.

La logique faible du second ordre, d’une force comparable à la précédente, permet de quantifier sur les sous-ensembles finis . Une structure face=F9828 a pour cette logique est une structure du premier ordre enrichie de la structure des ensembles héréditairement finis sur A. Cette logique permet d’exprimer les notions d’entier, d’ensemble fini, de suite finie, etc.

Mais les deux plus importantes familles d’extensions du premier ordre sont les logiques L^Q et L size=1^諸1 size=1^諸. Soit L un langage du premier ordre, Q un nouveau symbole qu’on fait fonctionner comme un quantificateur d’un genre nouveau. La morphologie de L^Q est celle de L, avec pour règle supplémentaire: si 﨏 est une formule, v une variable, Qv 﨏 est une formule. Différentes interprétations de Q conduisent à différentes logiques. La plus intéressante, actuellement, est celle dans laquelle Qv 﨏 signifie «il existe une infinité non dénombrable d’éléments v tels que 﨏». En effet, dans ce cas et en supposant l’alphabet de L dénombrable, L^Q vérifie des théorèmes de compacité et de complétude, exactement comme L. On obtient ainsi une formalisation adéquate, dans un cas précis, de l’idée intuitive de «nombreux» ou de «grand» sous-ensemble, si féconde un peu partout en mathématiques.

Enfin si, revenant à un langage L, nous admettons comme formules nouvelles les conjonctions et disjonctions dénombrables de formules, nous obtenons une logique appelée L size=1^諸1 size=1^諸, la plus simple des logiques infinitaires . Cette logique, et plus encore certains de ses fragments, dits admissibles , jouent un rôle central dans les recherches actuelles

(cf. RÉCURSIVITÉ, chap. 5).

Devant cette prolifération de logiques, on peut être tenté de rechercher des principes de classification. En particulier, il est intéressant de savoir si tel ou tel système est caractérisé par un certain ensemble de propriétés générales qu’on peut tenir pour naturelles. Toute une branche de la logique est née de cette question. C’est la théorie de modèles abstraite , dont le premier résultat, qui reste le plus frappant, est dû à P. Lindström: La logique du premier ordre est la seule logique close pour les connecteurs et quantificateurs (classiques) qui satisfasse les théorèmes de compacité et de Löwenheim-Skolem. Ce théorème, confirmant la place privilégiée qu’occupe la logique du premier ordre, apporte à la thèse de Hilbert une justification nouvelle, de nature mathématique, et montre assez bien que l’autoréférence ne conduit pas nécessairement au paradoxe ni à la stérilité, du moins dans les mains des logiciens.